青岛版数学八年级下第8章平面图形的全等与相似单元测试题及答案
文档属性
| 名称 | 青岛版数学八年级下第8章平面图形的全等与相似单元测试题及答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 460.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-15 00:00:00 | ||
图片预览



文档简介
第8章整章水平测试
一、精心选一选(每小题3分,共30分)
1.下面不是全等图形性质的是 【 】
(A)大小相同 (B)形状相同 (C)颜色相同 (D)周长相同
2.如果两个相似多边形的对应边的比是,那么它们的面积比是 【 】
(A) (B) (C) (D)
3.如图所示,在△ABC中,DE∥BC,AD=5,BD=10,AE=3,则CE的值为 【 】
(A)9 (B)6 (C)3 (D)4
4.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是 【 】
(A)AB=AC (B)BD=CD (C)∠B=∠C (D)∠BDA=∠CDA
5. 如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度为 【 】
(A) (B)1 (C) (D)
6.如图,一扇窗户打开后用窗钩AB可将其固定.这里所运用的几何道理是( )
(A)三角形的稳定性 (B)两点之间线段最短
(C)两点确定一条直线 (D)垂线段最短
7.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )
(A)甲 (B)乙 (C)丙 (D)丁
8. 如图,点是上任意一点,,还应补充一个条件,才能推出.从下列条件中补充一个条件,不一定能推出的是
【 】
(A) (B)
(C) (D)
9.已知△ABC的三条长分别为2cm,5cm,6cm,现将要利用长度为30cm和60cm的细木条各一根,做一个三角形木架与△ABC相似.要求以其中一根作为这个三角形木架的一边,将另一根截成两段(允许有余料,接头及损耗忽略不计)作为这个三角形木架的另外两边,那么这个三角形木架的三边长度分别为 【 】
(A)10cm,25cm,30cm (B)10cm,30cm,36cm或10cm,12cm,30cm
(C)10cm,30cm,36cm (D)10cm,25cm,30cm或12cm,30cm,36cm
10.如图所示,在中,是的中点,过点的直线交于点,若以为顶点的三角形和以为顶点的三角形相似,则的长为
【 】
(A)3 (B)3或 (C)3或 (D)
二、耐心填一填(每小题3分,共30分)
1.“泰山童子”是中华人民共和国第十一届全运会 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网" \t "_blank )的吉祥物.通过观察可以发现这两个“泰山童子” 全等形, 相似形.(填“是”或“不是”)
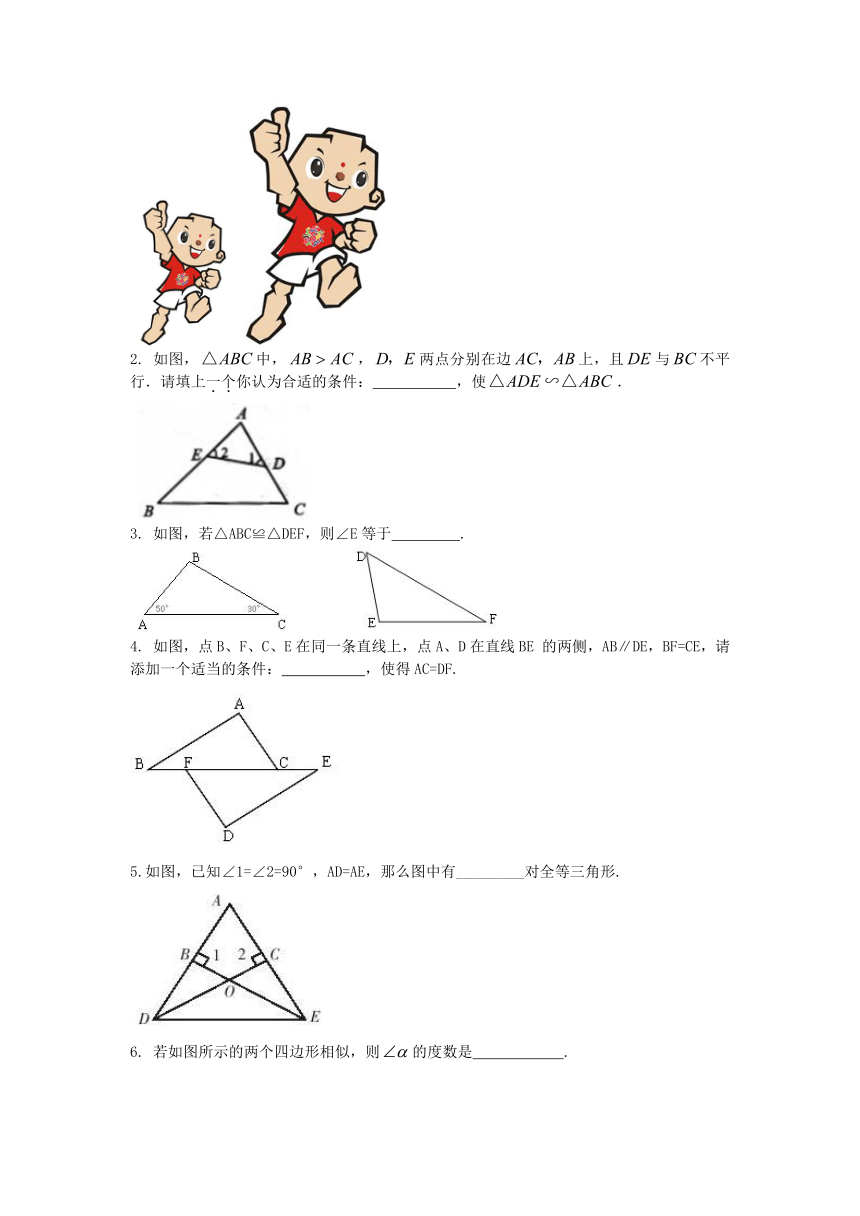
2. 如图,中,,两点分别在边上,且与不平行.请填上一个你认为合适的条件: ,使.
3. 如图,若△ABC≌△DEF,则∠E等于 .
4. 如图,点B、F、C、E在同一条直线上,点A、D在直线BE 的两侧,AB∥DE,BF=CE,请添加一个适当的条件: ,使得AC=DF.
5.如图,已知∠1=∠2=90°,AD=AE,那么图中有_________对全等三角形.
6. 若如图所示的两个四边形相似,则的度数是 .
7. 在△ABC中, AB=8,AC=6,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,则需添加的一个条件是 (写出一种情况即可).
8. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
9. 如图,丁轩同学在晚上由路灯走向路灯,当他走到点时,发现身后他影子的顶部刚好接触到路灯的底部,当他向前再步行20m到达点时,发现身前他影子的顶部刚好接触到路灯的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是 .
10. 在中,为直角,于点,,,写出其中的一对相似三角形是 和 ;并写出它的面积比 .
三、用心想一想(共48分)
1. (2011江苏连云港)两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?
2.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE。
(1)写出图中两对相似三角形(不得添加字母和线);
(2)请分别说明两对三角形相似的理由.
4如图,已知,,请说明下列结论成立的理由。
(1)≌; (2)∠C=∠D.
解:(1)在△ABC和△BAD中
≌
(2)≌
(2010四川自贡)如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离.
5. 如图,点是外的一点,分别在射线上取一点,使得,连结,所得与是否相似?证明你的结论.
四、拓广探索(12分)
小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心.小胖对小瘦说:“真可惜!我现在只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我就能将你跷到1.25米,甚至更高!”
(1)你认为小胖的话对吗?请你作图分析说明;
(2)你能否找到将小瘦翘到1.25高的方法?试说明.
八年级数学下册第8章整章水平测试参考答案:
一、1~10 CBBBC ACBDB
二、1. 不是 是 2.或 HYPERLINK "http://www." 或 3. 100°
4.AB=DE或∠A=∠D等 5.3 6. 7. ∠A= ∠D (或者BC:EF = 2:1)
8.22.5 9. 30m 10. ; 9∶16 或 ; 9∶25 或 ; 16∶25
三、解:全等 .理由如下:∵两三角形纸板完全相同,
∴BC=BF,AB=BD,∠A=∠D,
∴AB-BF=BD-BC,即AF=DC.
在△AOF和△DOC中,∵AF=DC,∠A=∠D,∠AOF=∠DOC,
∴△AOF≌△DOC(AAS).
解:(1)已知,BC,AB=BA,SSS
(2)∠C=∠D , 全等三角形的对应角相等.
解:作出示意图
连接AB,同时连结OC并延长交AB于E,
因为夹子是轴对称图形,故OE是对称轴
∴OE⊥AB AE=BE ∴Rt△OCD∽Rt△OAE
∴=
而OC===26
即= ∴AE==15
∴AB=2AE=30(mm)
答:AB两点间的距离为30mm.
由已知,
,同理
解:(1)小胖的话不对.如图1所示,OP是标准跷跷板支架的高度,AC是跷跷板一端(小瘦一端)能翘到的最高高度1米,BC为地面.
因为OP⊥BC,AC⊥BC,∠OBP=∠ABC,
所以△OBP∽△ABC,所以.
又因为标准的跷跷板BO=OA,
所以OP=0.5米.
若将两端同时都再伸长相同的长度,假设为a米(a>0),如图2所示,BD=AE=a米,
因为BO=OA,
所以BO+a=OA+a,即OD=OE.
所以,同理可证△DOP∽△DEF.
所以,由OP=0.5米,得EF=1米.
综上所述,跷跷板两边同时都伸长相同的一段长度,跷跷板能到的最高高度始终为支架OP高度的两倍,所以不可能翘得更高.
(2)方案一:如图3所示,保持BO长度不变,将OA延长一半至E,即只将小瘦一边伸长一半,使AE=OA,则,由△BOP∽△BEF,得,所以EF=1.25米.
方案二:如图4所示,只将支架升高0.125米.
因为,△B′O′P∽△B′A′C′,
又O′P=0.5+0.125=0.625米,
所以,所以A′C′=1.25米.
一、精心选一选(每小题3分,共30分)
1.下面不是全等图形性质的是 【 】
(A)大小相同 (B)形状相同 (C)颜色相同 (D)周长相同
2.如果两个相似多边形的对应边的比是,那么它们的面积比是 【 】
(A) (B) (C) (D)
3.如图所示,在△ABC中,DE∥BC,AD=5,BD=10,AE=3,则CE的值为 【 】
(A)9 (B)6 (C)3 (D)4
4.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是 【 】
(A)AB=AC (B)BD=CD (C)∠B=∠C (D)∠BDA=∠CDA
5. 如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度为 【 】
(A) (B)1 (C) (D)
6.如图,一扇窗户打开后用窗钩AB可将其固定.这里所运用的几何道理是( )
(A)三角形的稳定性 (B)两点之间线段最短
(C)两点确定一条直线 (D)垂线段最短
7.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )
(A)甲 (B)乙 (C)丙 (D)丁
8. 如图,点是上任意一点,,还应补充一个条件,才能推出.从下列条件中补充一个条件,不一定能推出的是
【 】
(A) (B)
(C) (D)
9.已知△ABC的三条长分别为2cm,5cm,6cm,现将要利用长度为30cm和60cm的细木条各一根,做一个三角形木架与△ABC相似.要求以其中一根作为这个三角形木架的一边,将另一根截成两段(允许有余料,接头及损耗忽略不计)作为这个三角形木架的另外两边,那么这个三角形木架的三边长度分别为 【 】
(A)10cm,25cm,30cm (B)10cm,30cm,36cm或10cm,12cm,30cm
(C)10cm,30cm,36cm (D)10cm,25cm,30cm或12cm,30cm,36cm
10.如图所示,在中,是的中点,过点的直线交于点,若以为顶点的三角形和以为顶点的三角形相似,则的长为
【 】
(A)3 (B)3或 (C)3或 (D)
二、耐心填一填(每小题3分,共30分)
1.“泰山童子”是中华人民共和国第十一届全运会 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网" \t "_blank )的吉祥物.通过观察可以发现这两个“泰山童子” 全等形, 相似形.(填“是”或“不是”)
2. 如图,中,,两点分别在边上,且与不平行.请填上一个你认为合适的条件: ,使.
3. 如图,若△ABC≌△DEF,则∠E等于 .
4. 如图,点B、F、C、E在同一条直线上,点A、D在直线BE 的两侧,AB∥DE,BF=CE,请添加一个适当的条件: ,使得AC=DF.
5.如图,已知∠1=∠2=90°,AD=AE,那么图中有_________对全等三角形.
6. 若如图所示的两个四边形相似,则的度数是 .
7. 在△ABC中, AB=8,AC=6,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,则需添加的一个条件是 (写出一种情况即可).
8. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
9. 如图,丁轩同学在晚上由路灯走向路灯,当他走到点时,发现身后他影子的顶部刚好接触到路灯的底部,当他向前再步行20m到达点时,发现身前他影子的顶部刚好接触到路灯的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是 .
10. 在中,为直角,于点,,,写出其中的一对相似三角形是 和 ;并写出它的面积比 .
三、用心想一想(共48分)
1. (2011江苏连云港)两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?
2.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE。
(1)写出图中两对相似三角形(不得添加字母和线);
(2)请分别说明两对三角形相似的理由.
4如图,已知,,请说明下列结论成立的理由。
(1)≌; (2)∠C=∠D.
解:(1)在△ABC和△BAD中
≌
(2)≌
(2010四川自贡)如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离.
5. 如图,点是外的一点,分别在射线上取一点,使得,连结,所得与是否相似?证明你的结论.
四、拓广探索(12分)
小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心.小胖对小瘦说:“真可惜!我现在只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我就能将你跷到1.25米,甚至更高!”
(1)你认为小胖的话对吗?请你作图分析说明;
(2)你能否找到将小瘦翘到1.25高的方法?试说明.
八年级数学下册第8章整章水平测试参考答案:
一、1~10 CBBBC ACBDB
二、1. 不是 是 2.或 HYPERLINK "http://www." 或 3. 100°
4.AB=DE或∠A=∠D等 5.3 6. 7. ∠A= ∠D (或者BC:EF = 2:1)
8.22.5 9. 30m 10. ; 9∶16 或 ; 9∶25 或 ; 16∶25
三、解:全等 .理由如下:∵两三角形纸板完全相同,
∴BC=BF,AB=BD,∠A=∠D,
∴AB-BF=BD-BC,即AF=DC.
在△AOF和△DOC中,∵AF=DC,∠A=∠D,∠AOF=∠DOC,
∴△AOF≌△DOC(AAS).
解:(1)已知,BC,AB=BA,SSS
(2)∠C=∠D , 全等三角形的对应角相等.
解:作出示意图
连接AB,同时连结OC并延长交AB于E,
因为夹子是轴对称图形,故OE是对称轴
∴OE⊥AB AE=BE ∴Rt△OCD∽Rt△OAE
∴=
而OC===26
即= ∴AE==15
∴AB=2AE=30(mm)
答:AB两点间的距离为30mm.
由已知,
,同理
解:(1)小胖的话不对.如图1所示,OP是标准跷跷板支架的高度,AC是跷跷板一端(小瘦一端)能翘到的最高高度1米,BC为地面.
因为OP⊥BC,AC⊥BC,∠OBP=∠ABC,
所以△OBP∽△ABC,所以.
又因为标准的跷跷板BO=OA,
所以OP=0.5米.
若将两端同时都再伸长相同的长度,假设为a米(a>0),如图2所示,BD=AE=a米,
因为BO=OA,
所以BO+a=OA+a,即OD=OE.
所以,同理可证△DOP∽△DEF.
所以,由OP=0.5米,得EF=1米.
综上所述,跷跷板两边同时都伸长相同的一段长度,跷跷板能到的最高高度始终为支架OP高度的两倍,所以不可能翘得更高.
(2)方案一:如图3所示,保持BO长度不变,将OA延长一半至E,即只将小瘦一边伸长一半,使AE=OA,则,由△BOP∽△BEF,得,所以EF=1.25米.
方案二:如图4所示,只将支架升高0.125米.
因为,△B′O′P∽△B′A′C′,
又O′P=0.5+0.125=0.625米,
所以,所以A′C′=1.25米.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
