2020-2021学年高二数学人教B版(2019)选择性必修第一册第二章平面解析几何小结(2)课件(共15张PPT)
文档属性
| 名称 | 2020-2021学年高二数学人教B版(2019)选择性必修第一册第二章平面解析几何小结(2)课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 21:18:34 | ||
图片预览










文档简介
(共41张PPT)
第二章
平面解析几何小结(2)
高二年级
数学
内容提要
5
选取适当的参数以简化计算
4
和弦长、弦中点有关的问题
1
点与直线、直线与直线的位置关系
2
直线与圆、圆与圆的位置关系
3
直线与椭圆、双曲线、抛物线的位置关系
1
点与直线、直线与直线的位置关系
点
到直线
的距离
两条直线
平行
垂直
例1
已知
为正方形的中心,且这个正方形的一条边所在的直线方程为
,求这个正方形其它三条边所在直线的方程.
分析
利用直线的平行和垂直关系设出含参数的直线方程,
再利用点G到四条直线的距离相等求出参数.
已知
为正方形的中心,且这个正
方形的一条边所在的直线方程为
,
解:设与已知边平行的对边所在的直线方程
为
,与已知边垂直
的两边所在的直线方程为
和
,
则由点G到四条边的距离相等得
解得
,
或
所以这个正方形其它三条边所在的直线方程为
即
题后总结
(1)要熟悉两条直线平行和垂直关系
的代数表示;
(2)要熟悉点到直线的距离等基本公式;
(3)注意数形结合,将相关知识学以致用.
2
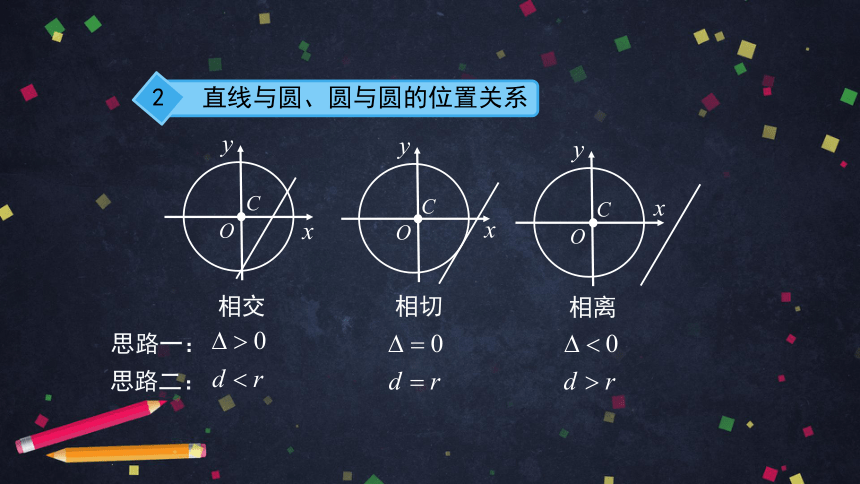
直线与圆、圆与圆的位置关系
思路二:
思路一:
相交
相切
相离
2
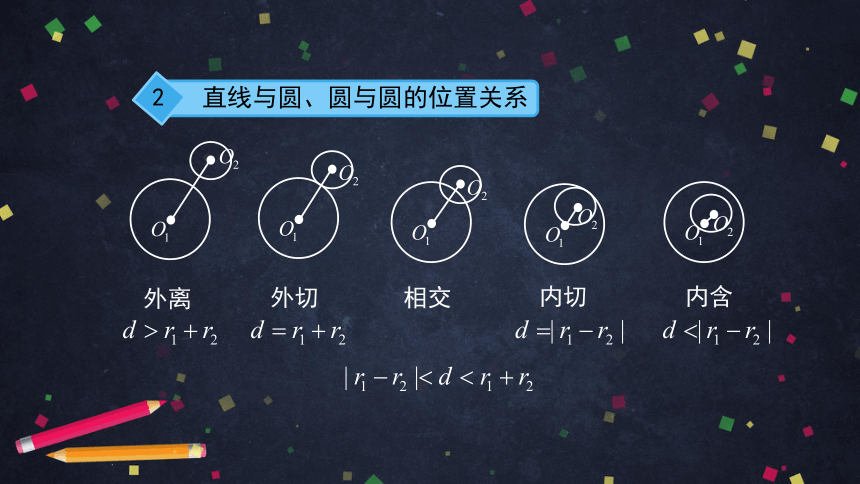
直线与圆、圆与圆的位置关系
外离
外切
相交
内切
内含
例2
过点
作圆
的两条切线PA和PB,切点分别为A和B,求直线AB的方程.
分析
①求出切线PA和PB;
②求出切点A和B的坐标;
③得出直线AB的方程.
解:点
,圆的标准方程为
设过点
的圆的切线为
,
(
不符合.)
设圆心为C,则
到切线的距离
得
即
解得
代入k的值,求切点A和B
?
计算难以实现!
另析
过圆心
作出半径CA和CB,连接PC,
则Rt△
和Rt△
有公共的斜边PC,
因为点
,
,
所以以PC为直径的圆方程为
另解:
所以P,A,C,B四点都在以PC为直径的圆上.
将其化为圆的一般方程为
而已知圆C的方程为
将两个方程作差得
因为切点A和B的坐标同时满足两个圆的方程,则它们必都满足这个直线的方程.
而过点A和点B的直线是唯一的,
所以
就是直线AB的方程.
题后总结
(1)做题之前先设计好解题思路;
(2)当一种解法遇到阻碍时要转换思路;
(3)如能利用平面几何的知识适当转化,
往往可以简化计算
.
3
直线与椭圆、双曲线、抛物线的位置关系
直线与椭圆只有一个公共点
直线与椭圆相切
直线与双曲线只有一个公共点
直线与双曲线相切
直线与抛物线只有一个公共点
直线与抛物线相切
联立方程,判断有几个根
例3
求过点
且与抛物线
只有一个公共点的直线的方程.
试解:设过点
的直线为
,与抛物线方程联立得
由
得
所以直线的方程为
正解:设过点
的直线为
,
由
得
所以直线方程为
.
与抛物线方程联立得
或
也满足.
①
时,方程为
,
公共点为
,满足.
或
或
.
②
时,
题后总结
(1)要多运用数形结合的思想帮助解题;
(2)注意直线斜率不存在的特殊情况;
(3)注意联立后的方程二次项系数是否为0
.
4
和弦长、弦中点有关的问题
则
设弦所在的直线方程为
弦端点为
,
,中点为
,
例4
已知椭圆的中心在坐标原点,焦点在坐标轴上,直线
和椭圆交于点P和点Q,且
,
求椭圆方程.
分析
如何设椭圆方程?
解1:设椭圆方程为
或
与
联立得
解2:设椭圆方程为
与
联立得
双曲线方程可设为
或
解2:与
联立得
因为有两个交点P和Q,所以
得
设两个交点为
,
则
“设而不求”
例4
已知椭圆的中心在坐标原点,焦点
坐标轴上,直线
和椭圆交于点P和点Q,且
,
,
求椭圆方程.
分析
垂直和弦长的已知条件如何利用?
由
得
即
由
得
所以
…………②
…………①
将
代入①②得
解得
或
且都满足
所以对应椭圆方程为
或
(其余同解2)
解3:由
且
,
设线段
中点为
,
则
所以
解得
或
再由
得到
或
题后总结
(1)要学会运用“设而不求”的思想;
(2)要熟悉弦长、中点坐标等的计算方法;
(3)如果有可能,要优先考虑平面几何转化.
5
选取适当的参数以简化计算
设直线
设椭圆
设双曲线
设直线
上点
设抛物线
上点
例5
过抛物线的顶点O作两条互相垂直的弦OA和OB.
求证:弦AB与抛物线的对称轴相交于定点.
分析
建系,
需要证明直线AB与
x
轴相交于定点.
设抛物线方程为
将直线OA的斜率设为参数k,
则直线OB的斜率为
,由此计算直线AB
.
根据抛物线方程,设A、B两点的坐标为
设直线AB方程为
或
(也可以设为
)
思路1:
思路2:
思路3:
解1:设直线OA的斜率为参数k,则直线OB的斜率为
,
分别与
联立解得
直线OA方程
和直线OB方程
则直线AB的方程为
所以弦AB与
x
轴相交于定点
为了证明它与
x
轴交于定点,取
代入得
这是一个与参数
k
无关的常数,
解2:设直线AB方程为
与
联立得
因为有两个交点A和B,所以
得
设两个交点为
,
,
则
“设而不求”
由
得
将
代入得
所以
(
舍).
所以直线AB方程为
,过定点
解3:因为AB两点的坐标满足抛物线方程,所以设为
则由
得
即
得
则直线AB的方程为
所以弦AB与
x
轴相交于定点
为了证明它与
x
轴交于定点,取
代入得
因为
,所以
题后总结
(1)找好解题的出发点,选择设点坐标或者设直线方程;
(2)尽量减少参数的个数;
(3)设计好解题思路,选择计算相对简单的思路.
课堂小结
(3)在直线和椭圆、双曲线、抛物线的关系中,更多的是依靠
直线方程或点坐标的代数运算.
其中注意“数形结合”、
“几何转化”、“设而不求”等思想的运用;
(1)要熟悉直线方程和圆锥曲线方程,及弦长、中点等求法;
(2)在点、直线、圆的相互关系中,优先从平行、垂直、距离
等平面几何角度考虑;
课后作业
(人教B版选修第一册2.3.4练习B第4题)
课后作业
(人教B版选修第一册第二章复习题B组第25题)
谢谢!
第二章
平面解析几何小结(2)
高二年级
数学
内容提要
5
选取适当的参数以简化计算
4
和弦长、弦中点有关的问题
1
点与直线、直线与直线的位置关系
2
直线与圆、圆与圆的位置关系
3
直线与椭圆、双曲线、抛物线的位置关系
1
点与直线、直线与直线的位置关系
点
到直线
的距离
两条直线
平行
垂直
例1
已知
为正方形的中心,且这个正方形的一条边所在的直线方程为
,求这个正方形其它三条边所在直线的方程.
分析
利用直线的平行和垂直关系设出含参数的直线方程,
再利用点G到四条直线的距离相等求出参数.
已知
为正方形的中心,且这个正
方形的一条边所在的直线方程为
,
解:设与已知边平行的对边所在的直线方程
为
,与已知边垂直
的两边所在的直线方程为
和
,
则由点G到四条边的距离相等得
解得
,
或
所以这个正方形其它三条边所在的直线方程为
即
题后总结
(1)要熟悉两条直线平行和垂直关系
的代数表示;
(2)要熟悉点到直线的距离等基本公式;
(3)注意数形结合,将相关知识学以致用.
2
直线与圆、圆与圆的位置关系
思路二:
思路一:
相交
相切
相离
2
直线与圆、圆与圆的位置关系
外离
外切
相交
内切
内含
例2
过点
作圆
的两条切线PA和PB,切点分别为A和B,求直线AB的方程.
分析
①求出切线PA和PB;
②求出切点A和B的坐标;
③得出直线AB的方程.
解:点
,圆的标准方程为
设过点
的圆的切线为
,
(
不符合.)
设圆心为C,则
到切线的距离
得
即
解得
代入k的值,求切点A和B
?
计算难以实现!
另析
过圆心
作出半径CA和CB,连接PC,
则Rt△
和Rt△
有公共的斜边PC,
因为点
,
,
所以以PC为直径的圆方程为
另解:
所以P,A,C,B四点都在以PC为直径的圆上.
将其化为圆的一般方程为
而已知圆C的方程为
将两个方程作差得
因为切点A和B的坐标同时满足两个圆的方程,则它们必都满足这个直线的方程.
而过点A和点B的直线是唯一的,
所以
就是直线AB的方程.
题后总结
(1)做题之前先设计好解题思路;
(2)当一种解法遇到阻碍时要转换思路;
(3)如能利用平面几何的知识适当转化,
往往可以简化计算
.
3
直线与椭圆、双曲线、抛物线的位置关系
直线与椭圆只有一个公共点
直线与椭圆相切
直线与双曲线只有一个公共点
直线与双曲线相切
直线与抛物线只有一个公共点
直线与抛物线相切
联立方程,判断有几个根
例3
求过点
且与抛物线
只有一个公共点的直线的方程.
试解:设过点
的直线为
,与抛物线方程联立得
由
得
所以直线的方程为
正解:设过点
的直线为
,
由
得
所以直线方程为
.
与抛物线方程联立得
或
也满足.
①
时,方程为
,
公共点为
,满足.
或
或
.
②
时,
题后总结
(1)要多运用数形结合的思想帮助解题;
(2)注意直线斜率不存在的特殊情况;
(3)注意联立后的方程二次项系数是否为0
.
4
和弦长、弦中点有关的问题
则
设弦所在的直线方程为
弦端点为
,
,中点为
,
例4
已知椭圆的中心在坐标原点,焦点在坐标轴上,直线
和椭圆交于点P和点Q,且
,
求椭圆方程.
分析
如何设椭圆方程?
解1:设椭圆方程为
或
与
联立得
解2:设椭圆方程为
与
联立得
双曲线方程可设为
或
解2:与
联立得
因为有两个交点P和Q,所以
得
设两个交点为
,
则
“设而不求”
例4
已知椭圆的中心在坐标原点,焦点
坐标轴上,直线
和椭圆交于点P和点Q,且
,
,
求椭圆方程.
分析
垂直和弦长的已知条件如何利用?
由
得
即
由
得
所以
…………②
…………①
将
代入①②得
解得
或
且都满足
所以对应椭圆方程为
或
(其余同解2)
解3:由
且
,
设线段
中点为
,
则
所以
解得
或
再由
得到
或
题后总结
(1)要学会运用“设而不求”的思想;
(2)要熟悉弦长、中点坐标等的计算方法;
(3)如果有可能,要优先考虑平面几何转化.
5
选取适当的参数以简化计算
设直线
设椭圆
设双曲线
设直线
上点
设抛物线
上点
例5
过抛物线的顶点O作两条互相垂直的弦OA和OB.
求证:弦AB与抛物线的对称轴相交于定点.
分析
建系,
需要证明直线AB与
x
轴相交于定点.
设抛物线方程为
将直线OA的斜率设为参数k,
则直线OB的斜率为
,由此计算直线AB
.
根据抛物线方程,设A、B两点的坐标为
设直线AB方程为
或
(也可以设为
)
思路1:
思路2:
思路3:
解1:设直线OA的斜率为参数k,则直线OB的斜率为
,
分别与
联立解得
直线OA方程
和直线OB方程
则直线AB的方程为
所以弦AB与
x
轴相交于定点
为了证明它与
x
轴交于定点,取
代入得
这是一个与参数
k
无关的常数,
解2:设直线AB方程为
与
联立得
因为有两个交点A和B,所以
得
设两个交点为
,
,
则
“设而不求”
由
得
将
代入得
所以
(
舍).
所以直线AB方程为
,过定点
解3:因为AB两点的坐标满足抛物线方程,所以设为
则由
得
即
得
则直线AB的方程为
所以弦AB与
x
轴相交于定点
为了证明它与
x
轴交于定点,取
代入得
因为
,所以
题后总结
(1)找好解题的出发点,选择设点坐标或者设直线方程;
(2)尽量减少参数的个数;
(3)设计好解题思路,选择计算相对简单的思路.
课堂小结
(3)在直线和椭圆、双曲线、抛物线的关系中,更多的是依靠
直线方程或点坐标的代数运算.
其中注意“数形结合”、
“几何转化”、“设而不求”等思想的运用;
(1)要熟悉直线方程和圆锥曲线方程,及弦长、中点等求法;
(2)在点、直线、圆的相互关系中,优先从平行、垂直、距离
等平面几何角度考虑;
课后作业
(人教B版选修第一册2.3.4练习B第4题)
课后作业
(人教B版选修第一册第二章复习题B组第25题)
谢谢!
