6.1菱形的性质与判定 课件(共22张PPT)
文档属性
| 名称 | 6.1菱形的性质与判定 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览







文档简介
第六章 特殊平行四边形
1 菱形的性质与判定
知识点一 菱形的定义
定义
符号语言
菱形
注意
知识点一 菱形的定义
定义
符号语言
菱形
一组邻边相等的平行四边形叫做菱形
如图所示,在平行
四边形ABCD中,若
AB=AD,则平行四
边形ABCD是菱形
注意
(1)菱形必须满足两个条件:一是平行四边形;二是一组邻边相等;
(2)菱形的定义既提供了菱形的基本性质,也提供了基本的判定方法
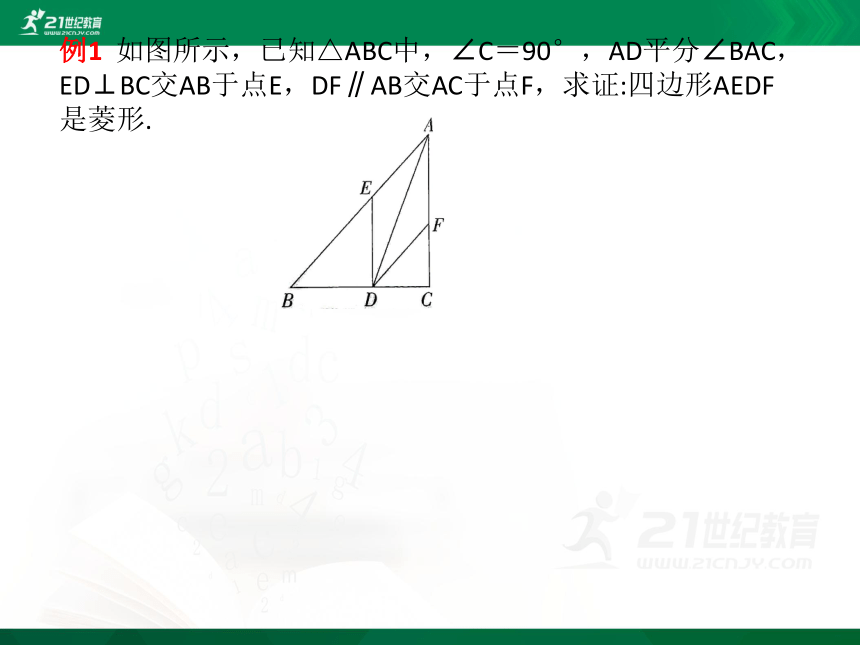
例1 如图所示,已知△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC交AB于点E,DF∥AB交AC于点F,求证:四边形AEDF是菱形.
例1 如图所示,已知△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC交AB于点E,DF∥AB交AC于点F,求证:四边形AEDF是菱形.
证明 ∵∠C=90°,ED⊥BC交AB于点E,∴DE∥AC,∵DF∥AB,∴四边形AEDF为平行四边形.
∵AD平分∠BAC,∴∠EAD=∠FAD.
又∵四边形AEDF为平行四边形,∴∠FAD=∠ADE,
∴∠EAD=∠ADE,∴AE=ED,∴四边形AEDF是菱形.
温馨提示 应用菱形的定义证明四边形是菱形时,先证明四边形是平行四边形,再证明一组邻边相等.
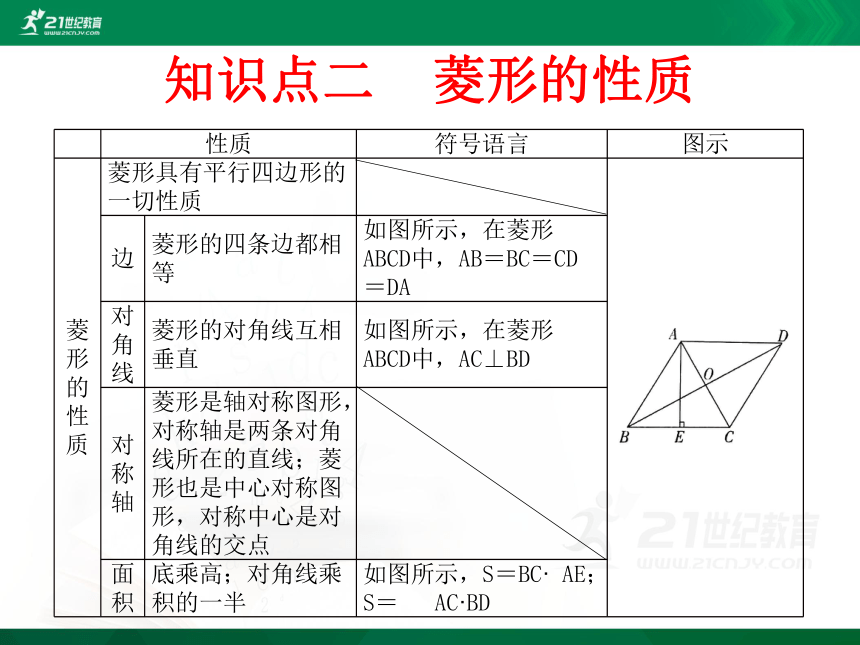
知识点二 菱形的性质
性质
符号语言
图示
菱形的性质
菱形具有平行四边形的一切性质
边
菱形的四条边都相等
如图所示,在菱形ABCD中,AB=BC=CD=DA
对角线
菱形的对角线互相垂直
如图所示,在菱形ABCD中,AC⊥BD
对称轴
菱形是轴对称图形,对称轴是两条对角线所在的直线;菱形也是中心对称图形,对称中心是对角线的交点
面积
底乘高;对角线乘积的一半
如图所示,S=BC· AE;S= AC·BD
例2 如图所示,在菱形ABCD中,AB=AC=2,对角线AC、BD相交于点O.
(1)求∠ABC的大小;
(2)求菱形ABCD的面积(结果保留根号).
例2 如图所示,在菱形ABCD中,AB=AC=2,对角线AC、BD相交于点O.
(1)求∠ABC的大小;
(2)求菱形ABCD的面积(结果保留根号).
解析 (1)∵四边形ABCD是菱形,∴AB=BC,∵AB=AC=2,
∴AB=BC=AC=2,∴△ABC是等边三角形,∴∠ABC=60°.
(2)∵四边形ABCD是菱形,∴BD⊥AC,OA=OC= AC=1,S菱形ABCD=2S△ABC,在Rt△AOB中,由勾股定理得OB= = = ,
∴S菱形ABCD=2S△ABC=2× ×2× =2 .
例2 如图所示,在菱形ABCD中,AB=AC=2,对角线AC、BD相交于点O.
(1)求∠ABC的大小;
(2)求菱形ABCD的面积(结果保留根号).
解析 (1)∵四边形ABCD是菱形,∴AB=BC,∵AB=AC=2,
∴AB=BC=AC=2,∴△ABC是等边三角形,∴∠ABC=60°.
(2)∵四边形ABCD是菱形,∴BD⊥AC,OA=OC= AC=1,S菱形ABCD=2S△ABC,在Rt△AOB中,由勾股定理得OB= = = ,
∴S菱形ABCD=2S△ABC=2× ×2× =2 .
温馨提示 在菱形中,若出现一条对角线与边相等,则会出现特殊的三角形——等边三角形.菱形的有关计算中,通常的辅助线是连接对角线,得到四个直角三角形,然后依据勾股定理求线段的长度.
知识点三 菱形的判定
判定方法
符号语言
图示
菱形的判定
边
一组邻边相等的平行四边形是菱形
如图所示,在平行四边形ABCD中,若AB=AD,则平行四边形ABCD是菱形
四条边都相等的四边形是菱形
如图所示,在四边形ABCD中,∵AB=BC=CD=DA,∴四边形ABCD是菱形
对角线
对角线互相垂直的平行四边形是菱形
如图所示,在平行四边形ABCD中,∵AC⊥BD,∴平行四边形ABCD是菱形
例3 如图所示,过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
例3 如图所示,过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
解析 四边形EFGH是菱形.
理由:在平行四边形ABCD中,OA=OC,AB∥CD,∴∠OAE=∠OCG,
在△AOE和△COG中, ∴△AOE≌△COG(ASA),
∴OE=OG,同理可得OF=OH,∴四边形EFGH是平行四边形,
∵EG⊥FH,∴四边形EFGH是菱形.
例3 如图所示,过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
解析 四边形EFGH是菱形.
理由:在平行四边形ABCD中,OA=OC,AB∥CD,∴∠OAE=∠OCG,
在△AOE和△COG中, ∴△AOE≌△COG(ASA),
∴OE=OG,同理可得OF=OH,∴四边形EFGH是平行四边形,
∵EG⊥FH,∴四边形EFGH是菱形.
温馨提示 在菱形的判定中,当应用对角线判定时,先证明四边形是平行四边形,再证明四边形的对角线互相垂直或直接证明四边形的对角线互相垂直平分.
经典例题
题型一 利用菱形的性质进行计算
例1 如图所示,在菱形ABCD中,E是AB边的中点,连接DE,DE⊥AB,对角线AC、BD交于点H.
(1)求∠ABC的度数;
(2)如果菱形的对角线AC=2 ,求菱形的面积.
分析 (1)在菱形ABCD中,E是AB边的中点,DE⊥AB,可得△ABD是等边三角形,进而可求∠ABC的度数;
(2)根据菱形的对角线AC=2 和勾股定理可求BH的长,进而可求菱形的面积.
解析 (1)在菱形ABCD中,E是AB边的中点,DE⊥AB,∴AD=DB=AB,∴△ABD是等边三角形,∴∠ABD=∠DAB=60°,∴∠ABC=120°.
(2)∵菱形的对角线AC=2 ,∴AH=HC= AC= ,
∵∠DBA=60°,∴∠HAB=30°,∴AB=2BH,
∴在Rt△ABH中,根据勾股定理,得AB2-BH2=AH2,
∴4BH2-BH2=( )2,∴BH=1(负值舍去),∴BD=2BH=2,
∴菱形的面积为 ×AC×BD= ×2 ×2=2 .
点拨 菱形被对角线分成四个全等的直角三角形,由此利用直角三角形的面积公式可以推知菱形的面积等于它的两条对角线乘积的一半.
题型二 探求判定菱形的条件
例2 如图所示,在△ABC中,D是AB边上的一点,且BD=BC,BE⊥CD于点E,延长BE交AC于点F,请再添加一个条件,使四边形DMCF是菱形,并加以证明.
解析 添加的条件:ME=FE.
理由:∵BD=BC,BE⊥CD,∴DE=EC,
又ME=FE,∴四边形DMCF为平行四边形,
又∵BE⊥CD,∴平行四边形DMCF是菱形.
点拨 本题是条件探索型题,往往采取“执果索因”的方法解题.
题型三 菱形的性质与判定的综合应用
例3 如图所示,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.求证:
(1)△ABE≌△ADE;
(2)四边形BFDE是菱形.
题型三 菱形的性质与判定的综合应用
例3 如图所示,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.求证:
(1)△ABE≌△ADE;
(2)四边形BFDE是菱形.
分析 (1)由菱形的性质得出AB=AD,∠BAE=∠DAE,由SAS即可得出△AB≌△ADE.
(2)连接BD,交AC于点O,由菱形的性质得出AC⊥BD,OA=OC,OB=OD,EF⊥BD,得出OE=OF,即可证出四边形BFDE是菱形.
证明:
(1)∵四边形ABCD是菱形,∴AB=AD,∠BAE=∠DAE.
在△ABE和△ADE中, ∴△ABE≌△ADE(SAS).
(2)连接BD,交AC于点O,
如下图所示.∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∵AE=CF,∴OE=OF,
∴四边形BFDE是平行四边形,又∵EF⊥BD,
∴平行四边形BFDE是菱形.
点拨 菱形的性质可以提供一些线段和角相等的条件,因此在证明三角形全等时,常常会应用到菱形的性质来解决问题.
1 菱形的性质与判定
知识点一 菱形的定义
定义
符号语言
菱形
注意
知识点一 菱形的定义
定义
符号语言
菱形
一组邻边相等的平行四边形叫做菱形
如图所示,在平行
四边形ABCD中,若
AB=AD,则平行四
边形ABCD是菱形
注意
(1)菱形必须满足两个条件:一是平行四边形;二是一组邻边相等;
(2)菱形的定义既提供了菱形的基本性质,也提供了基本的判定方法
例1 如图所示,已知△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC交AB于点E,DF∥AB交AC于点F,求证:四边形AEDF是菱形.
例1 如图所示,已知△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC交AB于点E,DF∥AB交AC于点F,求证:四边形AEDF是菱形.
证明 ∵∠C=90°,ED⊥BC交AB于点E,∴DE∥AC,∵DF∥AB,∴四边形AEDF为平行四边形.
∵AD平分∠BAC,∴∠EAD=∠FAD.
又∵四边形AEDF为平行四边形,∴∠FAD=∠ADE,
∴∠EAD=∠ADE,∴AE=ED,∴四边形AEDF是菱形.
温馨提示 应用菱形的定义证明四边形是菱形时,先证明四边形是平行四边形,再证明一组邻边相等.
知识点二 菱形的性质
性质
符号语言
图示
菱形的性质
菱形具有平行四边形的一切性质
边
菱形的四条边都相等
如图所示,在菱形ABCD中,AB=BC=CD=DA
对角线
菱形的对角线互相垂直
如图所示,在菱形ABCD中,AC⊥BD
对称轴
菱形是轴对称图形,对称轴是两条对角线所在的直线;菱形也是中心对称图形,对称中心是对角线的交点
面积
底乘高;对角线乘积的一半
如图所示,S=BC· AE;S= AC·BD
例2 如图所示,在菱形ABCD中,AB=AC=2,对角线AC、BD相交于点O.
(1)求∠ABC的大小;
(2)求菱形ABCD的面积(结果保留根号).
例2 如图所示,在菱形ABCD中,AB=AC=2,对角线AC、BD相交于点O.
(1)求∠ABC的大小;
(2)求菱形ABCD的面积(结果保留根号).
解析 (1)∵四边形ABCD是菱形,∴AB=BC,∵AB=AC=2,
∴AB=BC=AC=2,∴△ABC是等边三角形,∴∠ABC=60°.
(2)∵四边形ABCD是菱形,∴BD⊥AC,OA=OC= AC=1,S菱形ABCD=2S△ABC,在Rt△AOB中,由勾股定理得OB= = = ,
∴S菱形ABCD=2S△ABC=2× ×2× =2 .
例2 如图所示,在菱形ABCD中,AB=AC=2,对角线AC、BD相交于点O.
(1)求∠ABC的大小;
(2)求菱形ABCD的面积(结果保留根号).
解析 (1)∵四边形ABCD是菱形,∴AB=BC,∵AB=AC=2,
∴AB=BC=AC=2,∴△ABC是等边三角形,∴∠ABC=60°.
(2)∵四边形ABCD是菱形,∴BD⊥AC,OA=OC= AC=1,S菱形ABCD=2S△ABC,在Rt△AOB中,由勾股定理得OB= = = ,
∴S菱形ABCD=2S△ABC=2× ×2× =2 .
温馨提示 在菱形中,若出现一条对角线与边相等,则会出现特殊的三角形——等边三角形.菱形的有关计算中,通常的辅助线是连接对角线,得到四个直角三角形,然后依据勾股定理求线段的长度.
知识点三 菱形的判定
判定方法
符号语言
图示
菱形的判定
边
一组邻边相等的平行四边形是菱形
如图所示,在平行四边形ABCD中,若AB=AD,则平行四边形ABCD是菱形
四条边都相等的四边形是菱形
如图所示,在四边形ABCD中,∵AB=BC=CD=DA,∴四边形ABCD是菱形
对角线
对角线互相垂直的平行四边形是菱形
如图所示,在平行四边形ABCD中,∵AC⊥BD,∴平行四边形ABCD是菱形
例3 如图所示,过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
例3 如图所示,过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
解析 四边形EFGH是菱形.
理由:在平行四边形ABCD中,OA=OC,AB∥CD,∴∠OAE=∠OCG,
在△AOE和△COG中, ∴△AOE≌△COG(ASA),
∴OE=OG,同理可得OF=OH,∴四边形EFGH是平行四边形,
∵EG⊥FH,∴四边形EFGH是菱形.
例3 如图所示,过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
解析 四边形EFGH是菱形.
理由:在平行四边形ABCD中,OA=OC,AB∥CD,∴∠OAE=∠OCG,
在△AOE和△COG中, ∴△AOE≌△COG(ASA),
∴OE=OG,同理可得OF=OH,∴四边形EFGH是平行四边形,
∵EG⊥FH,∴四边形EFGH是菱形.
温馨提示 在菱形的判定中,当应用对角线判定时,先证明四边形是平行四边形,再证明四边形的对角线互相垂直或直接证明四边形的对角线互相垂直平分.
经典例题
题型一 利用菱形的性质进行计算
例1 如图所示,在菱形ABCD中,E是AB边的中点,连接DE,DE⊥AB,对角线AC、BD交于点H.
(1)求∠ABC的度数;
(2)如果菱形的对角线AC=2 ,求菱形的面积.
分析 (1)在菱形ABCD中,E是AB边的中点,DE⊥AB,可得△ABD是等边三角形,进而可求∠ABC的度数;
(2)根据菱形的对角线AC=2 和勾股定理可求BH的长,进而可求菱形的面积.
解析 (1)在菱形ABCD中,E是AB边的中点,DE⊥AB,∴AD=DB=AB,∴△ABD是等边三角形,∴∠ABD=∠DAB=60°,∴∠ABC=120°.
(2)∵菱形的对角线AC=2 ,∴AH=HC= AC= ,
∵∠DBA=60°,∴∠HAB=30°,∴AB=2BH,
∴在Rt△ABH中,根据勾股定理,得AB2-BH2=AH2,
∴4BH2-BH2=( )2,∴BH=1(负值舍去),∴BD=2BH=2,
∴菱形的面积为 ×AC×BD= ×2 ×2=2 .
点拨 菱形被对角线分成四个全等的直角三角形,由此利用直角三角形的面积公式可以推知菱形的面积等于它的两条对角线乘积的一半.
题型二 探求判定菱形的条件
例2 如图所示,在△ABC中,D是AB边上的一点,且BD=BC,BE⊥CD于点E,延长BE交AC于点F,请再添加一个条件,使四边形DMCF是菱形,并加以证明.
解析 添加的条件:ME=FE.
理由:∵BD=BC,BE⊥CD,∴DE=EC,
又ME=FE,∴四边形DMCF为平行四边形,
又∵BE⊥CD,∴平行四边形DMCF是菱形.
点拨 本题是条件探索型题,往往采取“执果索因”的方法解题.
题型三 菱形的性质与判定的综合应用
例3 如图所示,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.求证:
(1)△ABE≌△ADE;
(2)四边形BFDE是菱形.
题型三 菱形的性质与判定的综合应用
例3 如图所示,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.求证:
(1)△ABE≌△ADE;
(2)四边形BFDE是菱形.
分析 (1)由菱形的性质得出AB=AD,∠BAE=∠DAE,由SAS即可得出△AB≌△ADE.
(2)连接BD,交AC于点O,由菱形的性质得出AC⊥BD,OA=OC,OB=OD,EF⊥BD,得出OE=OF,即可证出四边形BFDE是菱形.
证明:
(1)∵四边形ABCD是菱形,∴AB=AD,∠BAE=∠DAE.
在△ABE和△ADE中, ∴△ABE≌△ADE(SAS).
(2)连接BD,交AC于点O,
如下图所示.∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∵AE=CF,∴OE=OF,
∴四边形BFDE是平行四边形,又∵EF⊥BD,
∴平行四边形BFDE是菱形.
点拨 菱形的性质可以提供一些线段和角相等的条件,因此在证明三角形全等时,常常会应用到菱形的性质来解决问题.
