第一讲 算法与程序框图
图片预览

文档简介
第一讲 算法与程序框图
姓名: 学校: 年级:
【知识要点】
算法的概念:在数学中,算法通常是指按照一定规则解决某一类问题的明确和有限的步骤
算法的表示方法:1、使用自然语言描述算法2、使用流程图描述算法
概念:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.在程
序框图中,一个或几个程序框的组合表示算法中的一个步骤;带有方向箭头的流程线将程序
框连接起来,表示算法步骤的执行顺序
2.程序框的功能:
程序框 名称 功能
起止框 表示一个算法的起始和结束,是任何流程图不可少的.
输入、输出框 表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置.
处理框 赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内.
判断框 判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”.
流程线 连接程序框
连接点 连接程序框的两部份
3.画程序框图的规则如下:
(1)使用标准的图形符号.
(2)框图一般按从上到下、从左到右的方向画.
(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框具有超过一个退出点的唯一符号.
(4)判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.
(5)在图形符号内描述的语言要非常简练清楚.
(二)算法的基本逻辑结构
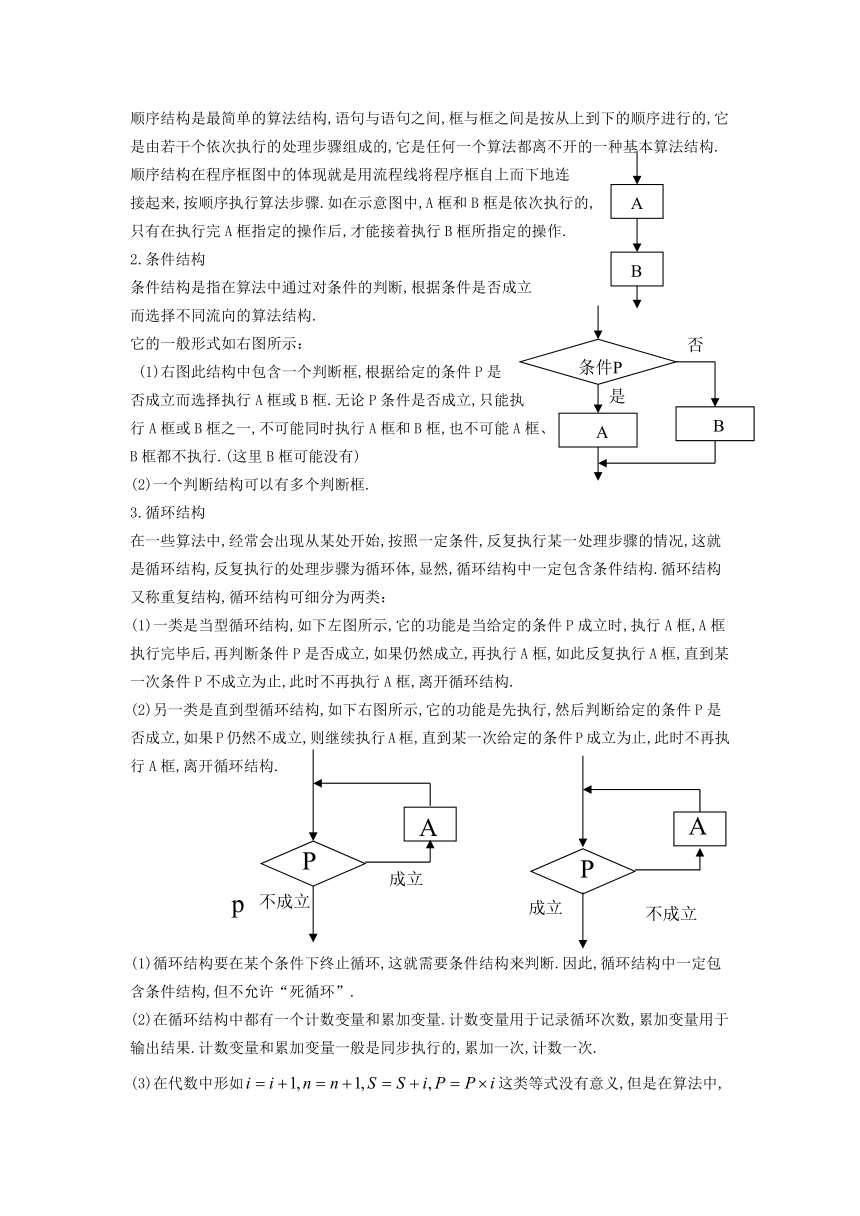
1.顺序结构
顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构.
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连
接起来,按顺序执行算法步骤.如在示意图中,A框和B框是依次执行的,
只有在执行完A框指定的操作后,才能接着执行B框所指定的操作.
2.条件结构
条件结构是指在算法中通过对条件的判断,根据条件是否成立
而选择不同流向的算法结构.
它的一般形式如右图所示:
(1)右图此结构中包含一个判断框,根据给定的条件P是
否成立而选择执行A框或B框.无论P条件是否成立,只能执
行A框或B框之一,不可能同时执行A框和B框,也不可能A框、
B框都不执行.(这里B框可能没有)
(2)一个判断结构可以有多个判断框.
3.循环结构
在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构.循环结构又称重复结构,循环结构可细分为两类:
(1)一类是当型循环结构,如下左图所示,它的功能是当给定的条件P成立时,执行A框,A框执行完毕后,再判断条件P是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次条件P不成立为止,此时不再执行A框,离开循环结构.
(2)另一类是直到型循环结构,如下右图所示,它的功能是先执行,然后判断给定的条件P是否成立,如果P仍然不成立,则继续执行A框,直到某一次给定的条件P成立为止,此时不再执行A框,离开循环结构.
(1)循环结构要在某个条件下终止循环,这就需要条件结构来判断.因此,循环结构中一定包含条件结构,但不允许“死循环”.
(2)在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果.计数变量和累加变量一般是同步执行的,累加一次,计数一次.
(3)在代数中形如这类等式没有意义,但是在算法中,这些扽是不再称为等式,而称为赋值语句,他们具有明显的意义:计算等号右边的式子值,并仍用原符号表示.
4.程序框图的记忆要诀:
(1)起始框有一条流出线,终止框有一条流入线;
(2)输入、输出和处理框有一条流入线和一条流程线;
(3)判断框有一条流入线和两条流出线;
(4)循环结构实质上是判断和处理的结合,可先判断再处理,也可先处理在判断.
【典型例题】
例1 下面几个说法正确的是________
①任何一个算法都离不开顺序结构;
②程序框图中,根据条件是否成立有不同的流向;
③任何一个算法都必须同时含有三种基本结构;
④顺序结构只有一个出口,条件结构有两个出口;
⑤循环结构中必须有条件结构,条件结构中也一定有循环结构.
例2 解决下列问题的算法中,必须含有条件结构的是( )
A.已知点的坐标和直线方程,求点到直线的距离
B.已知梯形两底及其高,求其面积
C.解一元二次方程
D.求两个实数的积
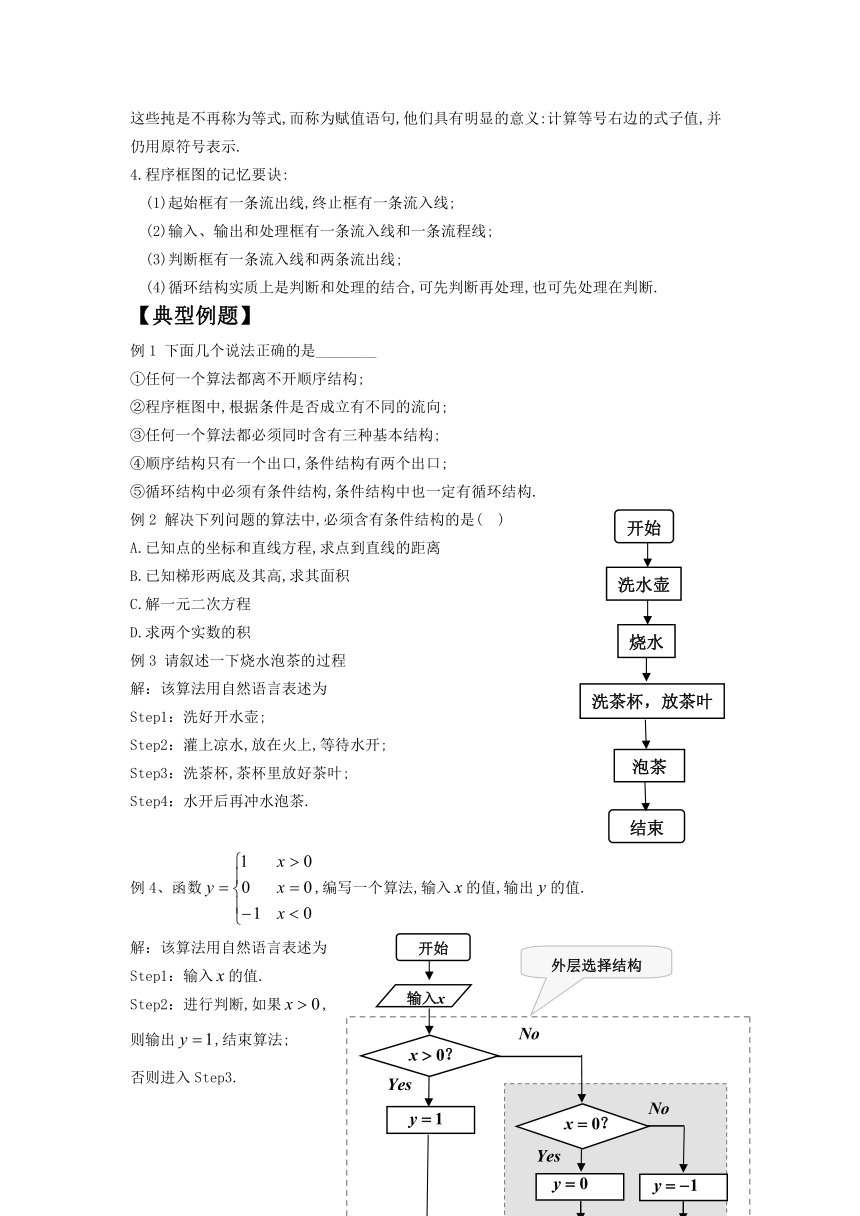
例3 请叙述一下烧水泡茶的过程
解:该算法用自然语言表述为
Step1:洗好开水壶;
Step2:灌上凉水,放在火上,等待水开;
Step3:洗茶杯,茶杯里放好茶叶;
Step4:水开后再冲水泡茶.
例4、函数,编写一个算法,输入的值,输出的值.
解:该算法用自然语言表述为
Step1:输入的值.
Step2:进行判断,如果,
则输出,结束算法;
否则进入Step3.
Step3:进行判断,如果,
则输出,结束算法;
否则输出,结束算法.
程序框图为:
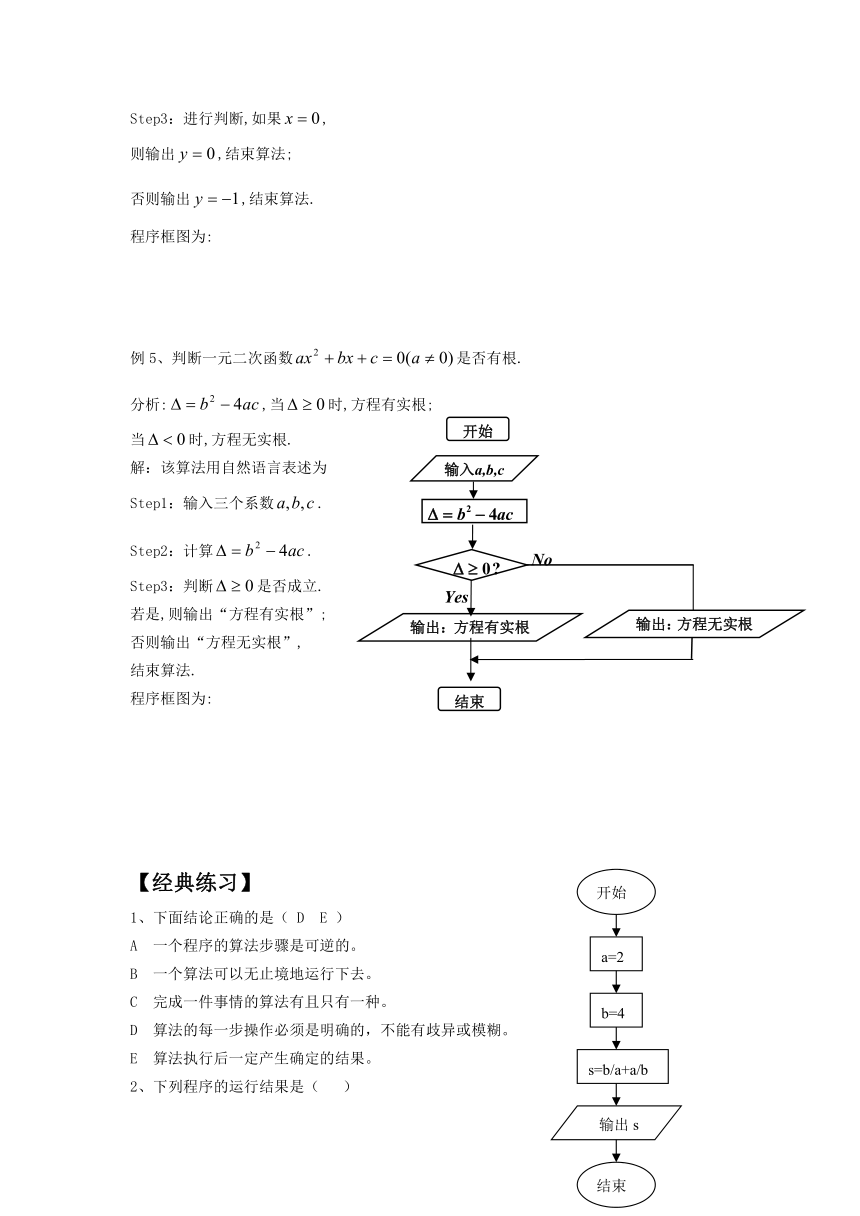
例5、判断一元二次函数是否有根.
分析:,当时,方程有实根;
当时,方程无实根.
解:该算法用自然语言表述为
Step1:输入三个系数.
Step2:计算.
Step3:判断是否成立.
若是,则输出“方程有实根”;
否则输出“方程无实根”,
结束算法.
程序框图为:
【经典练习】
1、下面结论正确的是( D E )
A 一个程序的算法步骤是可逆的。
B 一个算法可以无止境地运行下去。
C 完成一件事情的算法有且只有一种。
D 算法的每一步操作必须是明确的,不能有歧异或模糊。
E 算法执行后一定产生确定的结果。
2、下列程序的运行结果是( )
A. 2 B. 2.5 C. 4 D. 3.5
3、到银行办理个人异地汇款(不超过1000万)时,银行要收取一定的手续费,汇款额不超过100元,收取1元手续费,超过100元不超过5000元,按汇款的1%收取;超过5000元不超过1000000,一律收取50元手续费。设计算法求汇款额为x元时,银行收取的手续费y元,并画出程序框图。
4、以下给出的是计算…+的值的一个程序框图(如图),其中判断框内应填入的条件是(A )
A i>10 B i<10 C i>20 D i<20
5、如图所示,框图所给的程序运行的结果为s=90,那么判断框中应填入的关于k判断条件是 k<9 .
6、设计一个算法计算.
解:算法如下:第一步:输入(这里).
第二步:,.
第三步:,.
第四步:如果不大于,返回第三步;否则,算法结束.
最后得到的值就是的值.
7、乘坐火车时,可以托运货物,从甲地到乙地,规定每张火车客票托运费计算方法是:行李质量不超过时按元;超过而不超过时,其超过部分按元;超过时,其超过部分按元.编写程序,输入行李的质量,计算出托运的费用.
解:算法分析:数学模型实际上为:关于的分段函数.关系式
为:,
算法步骤:
第一步 输入行李质量.
第二步 当时,计算,否则,执行下一步.
第三步 当时,计算,否则,计算.
第四步 输出托运费.
程序框图为:略
【课后作业】
1.设计一个算法计算.
解:算法如下:第一步:输入(这里).
第二步:,.
第三步:,.
第四步:如果不大于,返回第三步;否则,算法结束.
最后得到的值就是的值.
程序框图为:略
2.下面算法的结果是( )
S1
S2
S3 如果则转S2
S4 输出
A.1024 B.512 C.8192 D.16384
3.求某生三门成绩的平均值,画出程序框图:
4.已知一个三角形的三边长分别是,它的面积可用海伦—秦九韶公式计算.
,其中.为计算机设计一个算法,输入三角形的三条边长,输出三角形的面积.
提示:该算法用自然语言表述为
Step1:输入三角形三边边长;
Step2:计算;
Step3:计算;
Step4:输出三角形的面积.
程序框图为
程序:
INPUT a,b,c
P=(a+b+c)/2
s=SQR(s*(s-a)*(s-b)*(s-c))
PRINT “area=”;s
END
5. 画出求实数的绝对值的框架图.
提示:程序1:
INPUT x
IF x>=0 THEN
PRINT x
ELSE
PRINT –x
END IF
END
程序1:
INPUT x
IF <0 THEN
x=-x
END IF
PRINT x
END
A
B
否
是
条件P
A
B
A
成立
不成立
P
不成立
P
成立
A
p
开始
洗水壶
烧水
泡茶
洗茶杯,放茶叶
结束
开始
输入x
输出y
外层选择结构
内层选择结构
结束
输出:方程有实根
开始
输入a,b,c
结束
输出:方程无实根
开始
a=2
b=4
s=b/a+a/b
输出s
结束
是
否
是
否
是
否
y=50
开始
输入x
x≤100
x≤5000
y=1
y=x*1%
x ≤1000000
输出”输入有误”
结束
是
否
开始
S=0, n=2, i=1
S=S+
输出S
n=n+2
i=i+1
结束
否
是
开始
k=10,s=1
s=s*k
k=k-1
输出s
结束
A←(a+b+c)/3
结束
开始
输出A
输入a,b,c
开始
输出S
结束
输入a,b,c
开始
输入x
输出y
结束
姓名: 学校: 年级:
【知识要点】
算法的概念:在数学中,算法通常是指按照一定规则解决某一类问题的明确和有限的步骤
算法的表示方法:1、使用自然语言描述算法2、使用流程图描述算法
概念:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.在程
序框图中,一个或几个程序框的组合表示算法中的一个步骤;带有方向箭头的流程线将程序
框连接起来,表示算法步骤的执行顺序
2.程序框的功能:
程序框 名称 功能
起止框 表示一个算法的起始和结束,是任何流程图不可少的.
输入、输出框 表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置.
处理框 赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内.
判断框 判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”.
流程线 连接程序框
连接点 连接程序框的两部份
3.画程序框图的规则如下:
(1)使用标准的图形符号.
(2)框图一般按从上到下、从左到右的方向画.
(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框具有超过一个退出点的唯一符号.
(4)判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.
(5)在图形符号内描述的语言要非常简练清楚.
(二)算法的基本逻辑结构
1.顺序结构
顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构.
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连
接起来,按顺序执行算法步骤.如在示意图中,A框和B框是依次执行的,
只有在执行完A框指定的操作后,才能接着执行B框所指定的操作.
2.条件结构
条件结构是指在算法中通过对条件的判断,根据条件是否成立
而选择不同流向的算法结构.
它的一般形式如右图所示:
(1)右图此结构中包含一个判断框,根据给定的条件P是
否成立而选择执行A框或B框.无论P条件是否成立,只能执
行A框或B框之一,不可能同时执行A框和B框,也不可能A框、
B框都不执行.(这里B框可能没有)
(2)一个判断结构可以有多个判断框.
3.循环结构
在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构.循环结构又称重复结构,循环结构可细分为两类:
(1)一类是当型循环结构,如下左图所示,它的功能是当给定的条件P成立时,执行A框,A框执行完毕后,再判断条件P是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次条件P不成立为止,此时不再执行A框,离开循环结构.
(2)另一类是直到型循环结构,如下右图所示,它的功能是先执行,然后判断给定的条件P是否成立,如果P仍然不成立,则继续执行A框,直到某一次给定的条件P成立为止,此时不再执行A框,离开循环结构.
(1)循环结构要在某个条件下终止循环,这就需要条件结构来判断.因此,循环结构中一定包含条件结构,但不允许“死循环”.
(2)在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果.计数变量和累加变量一般是同步执行的,累加一次,计数一次.
(3)在代数中形如这类等式没有意义,但是在算法中,这些扽是不再称为等式,而称为赋值语句,他们具有明显的意义:计算等号右边的式子值,并仍用原符号表示.
4.程序框图的记忆要诀:
(1)起始框有一条流出线,终止框有一条流入线;
(2)输入、输出和处理框有一条流入线和一条流程线;
(3)判断框有一条流入线和两条流出线;
(4)循环结构实质上是判断和处理的结合,可先判断再处理,也可先处理在判断.
【典型例题】
例1 下面几个说法正确的是________
①任何一个算法都离不开顺序结构;
②程序框图中,根据条件是否成立有不同的流向;
③任何一个算法都必须同时含有三种基本结构;
④顺序结构只有一个出口,条件结构有两个出口;
⑤循环结构中必须有条件结构,条件结构中也一定有循环结构.
例2 解决下列问题的算法中,必须含有条件结构的是( )
A.已知点的坐标和直线方程,求点到直线的距离
B.已知梯形两底及其高,求其面积
C.解一元二次方程
D.求两个实数的积
例3 请叙述一下烧水泡茶的过程
解:该算法用自然语言表述为
Step1:洗好开水壶;
Step2:灌上凉水,放在火上,等待水开;
Step3:洗茶杯,茶杯里放好茶叶;
Step4:水开后再冲水泡茶.
例4、函数,编写一个算法,输入的值,输出的值.
解:该算法用自然语言表述为
Step1:输入的值.
Step2:进行判断,如果,
则输出,结束算法;
否则进入Step3.
Step3:进行判断,如果,
则输出,结束算法;
否则输出,结束算法.
程序框图为:
例5、判断一元二次函数是否有根.
分析:,当时,方程有实根;
当时,方程无实根.
解:该算法用自然语言表述为
Step1:输入三个系数.
Step2:计算.
Step3:判断是否成立.
若是,则输出“方程有实根”;
否则输出“方程无实根”,
结束算法.
程序框图为:
【经典练习】
1、下面结论正确的是( D E )
A 一个程序的算法步骤是可逆的。
B 一个算法可以无止境地运行下去。
C 完成一件事情的算法有且只有一种。
D 算法的每一步操作必须是明确的,不能有歧异或模糊。
E 算法执行后一定产生确定的结果。
2、下列程序的运行结果是( )
A. 2 B. 2.5 C. 4 D. 3.5
3、到银行办理个人异地汇款(不超过1000万)时,银行要收取一定的手续费,汇款额不超过100元,收取1元手续费,超过100元不超过5000元,按汇款的1%收取;超过5000元不超过1000000,一律收取50元手续费。设计算法求汇款额为x元时,银行收取的手续费y元,并画出程序框图。
4、以下给出的是计算…+的值的一个程序框图(如图),其中判断框内应填入的条件是(A )
A i>10 B i<10 C i>20 D i<20
5、如图所示,框图所给的程序运行的结果为s=90,那么判断框中应填入的关于k判断条件是 k<9 .
6、设计一个算法计算.
解:算法如下:第一步:输入(这里).
第二步:,.
第三步:,.
第四步:如果不大于,返回第三步;否则,算法结束.
最后得到的值就是的值.
7、乘坐火车时,可以托运货物,从甲地到乙地,规定每张火车客票托运费计算方法是:行李质量不超过时按元;超过而不超过时,其超过部分按元;超过时,其超过部分按元.编写程序,输入行李的质量,计算出托运的费用.
解:算法分析:数学模型实际上为:关于的分段函数.关系式
为:,
算法步骤:
第一步 输入行李质量.
第二步 当时,计算,否则,执行下一步.
第三步 当时,计算,否则,计算.
第四步 输出托运费.
程序框图为:略
【课后作业】
1.设计一个算法计算.
解:算法如下:第一步:输入(这里).
第二步:,.
第三步:,.
第四步:如果不大于,返回第三步;否则,算法结束.
最后得到的值就是的值.
程序框图为:略
2.下面算法的结果是( )
S1
S2
S3 如果则转S2
S4 输出
A.1024 B.512 C.8192 D.16384
3.求某生三门成绩的平均值,画出程序框图:
4.已知一个三角形的三边长分别是,它的面积可用海伦—秦九韶公式计算.
,其中.为计算机设计一个算法,输入三角形的三条边长,输出三角形的面积.
提示:该算法用自然语言表述为
Step1:输入三角形三边边长;
Step2:计算;
Step3:计算;
Step4:输出三角形的面积.
程序框图为
程序:
INPUT a,b,c
P=(a+b+c)/2
s=SQR(s*(s-a)*(s-b)*(s-c))
PRINT “area=”;s
END
5. 画出求实数的绝对值的框架图.
提示:程序1:
INPUT x
IF x>=0 THEN
PRINT x
ELSE
PRINT –x
END IF
END
程序1:
INPUT x
IF <0 THEN
x=-x
END IF
PRINT x
END
A
B
否
是
条件P
A
B
A
成立
不成立
P
不成立
P
成立
A
p
开始
洗水壶
烧水
泡茶
洗茶杯,放茶叶
结束
开始
输入x
输出y
外层选择结构
内层选择结构
结束
输出:方程有实根
开始
输入a,b,c
结束
输出:方程无实根
开始
a=2
b=4
s=b/a+a/b
输出s
结束
是
否
是
否
是
否
y=50
开始
输入x
x≤100
x≤5000
y=1
y=x*1%
x ≤1000000
输出”输入有误”
结束
是
否
开始
S=0, n=2, i=1
S=S+
输出S
n=n+2
i=i+1
结束
否
是
开始
k=10,s=1
s=s*k
k=k-1
输出s
结束
A←(a+b+c)/3
结束
开始
输出A
输入a,b,c
开始
输出S
结束
输入a,b,c
开始
输入x
输出y
结束
