2020-2021学年高一数学人教A版必修2第一章1.2.1 中心投影与平行投影课件(39张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修2第一章1.2.1 中心投影与平行投影课件(39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 13:34:24 | ||
图片预览








文档简介
1.2.1空间几何体的三视图
学习目标:
1、了解中心投影和平行投影的原理;
2、能利用正投影绘制空间图形的三视图, 并根据所给的三视图识别该几何体;
3、能利用正投影绘制简单组合体的三视图,并根据所给的三视图说出该几何体由那些简单几何体构成。
请同学们看下面几个常见的自然现象,考虑它们是怎样得到的?
这种现象我们把它称为是投影
引入新课
投影是光线(投射线)通过物体,向选定的面(投影面)投射,并在该面上得到图形的方法.
通过观察和自己的认识 , 你是怎样来理解投影的含义的?
想一想?
引入新课
A
D
C
B
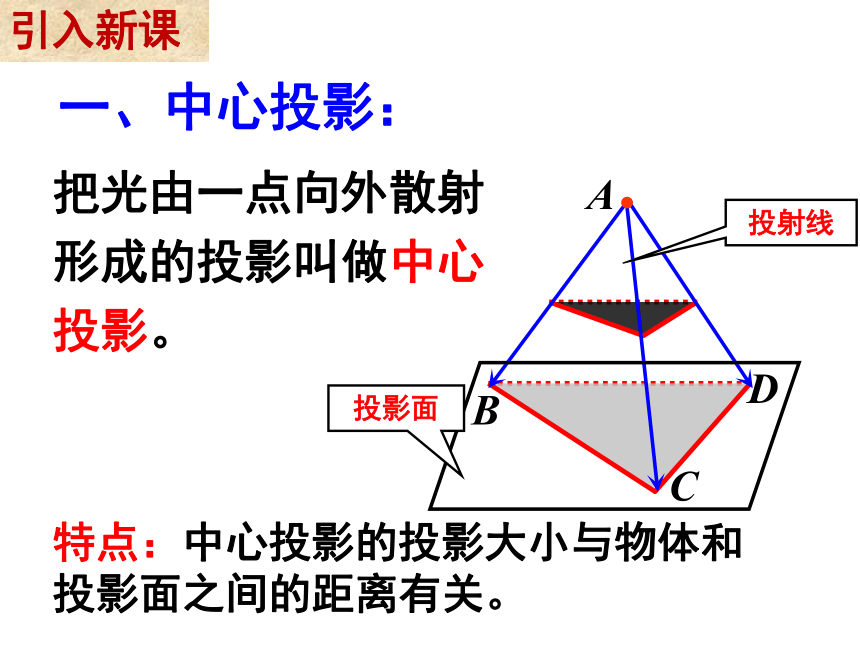
一、中心投影:
投射线
投影面
把光由一点向外散射形成的投影叫做中心投影。
特点:中心投影的投影大小与物体和投影面之间的距离有关。
引入新课
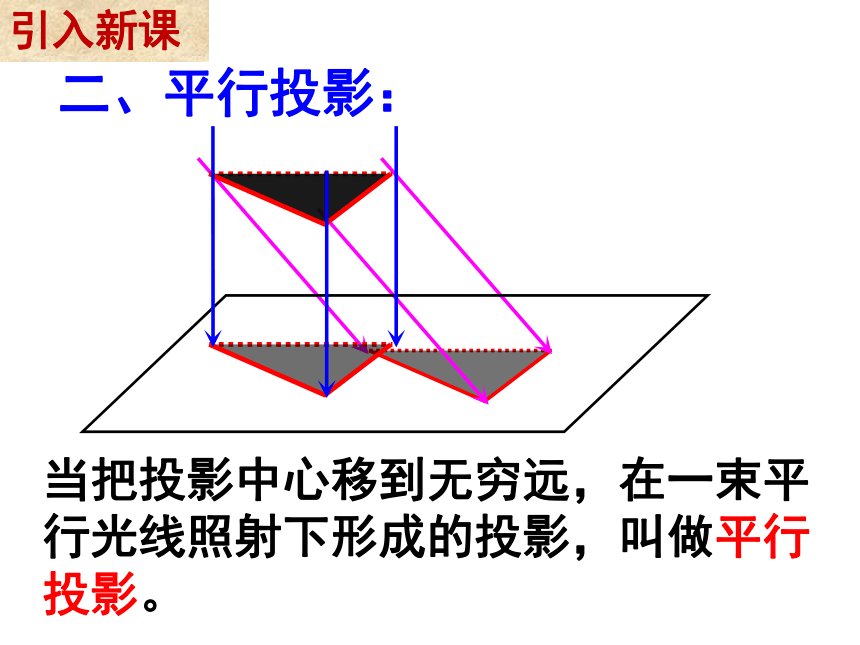
二、平行投影:
当把投影中心移到无穷远,在一束平行光线照射下形成的投影,叫做平行投影。
引入新课
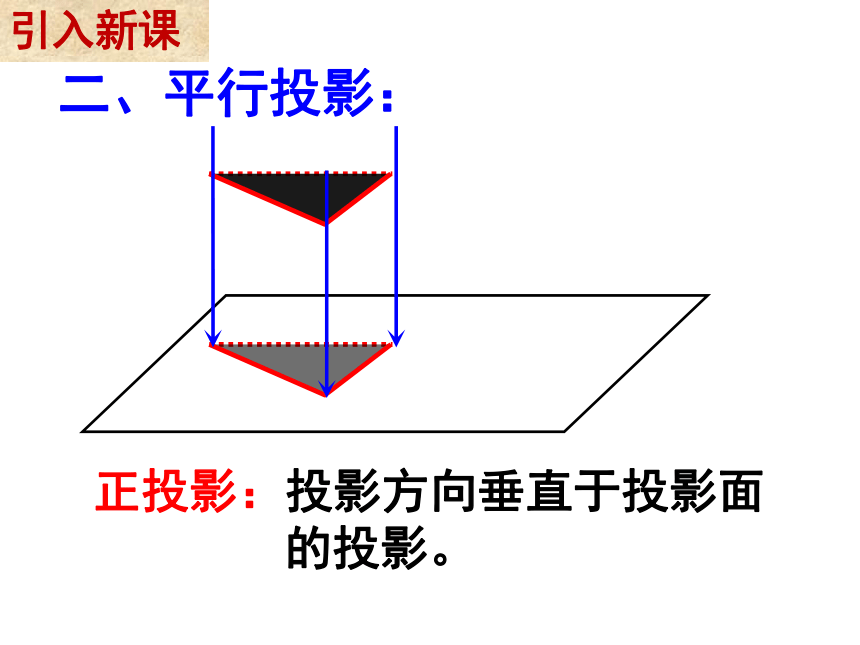
二、平行投影:
正投影:投影方向垂直于投影面
的投影。
引入新课
二、平行投影:
斜投影:投影方向与投影面倾斜
的投影。
引入新课
投影
平行投影
中心投影
斜投影
正投影
本节主要学习利用正投影绘制空间图形的三视图,并能根据所给的三视图了解该空间图形的基本特征。
引入新课
猜猜他们是什么关系?
引入新课
看事物不能只看单方面
引入新课
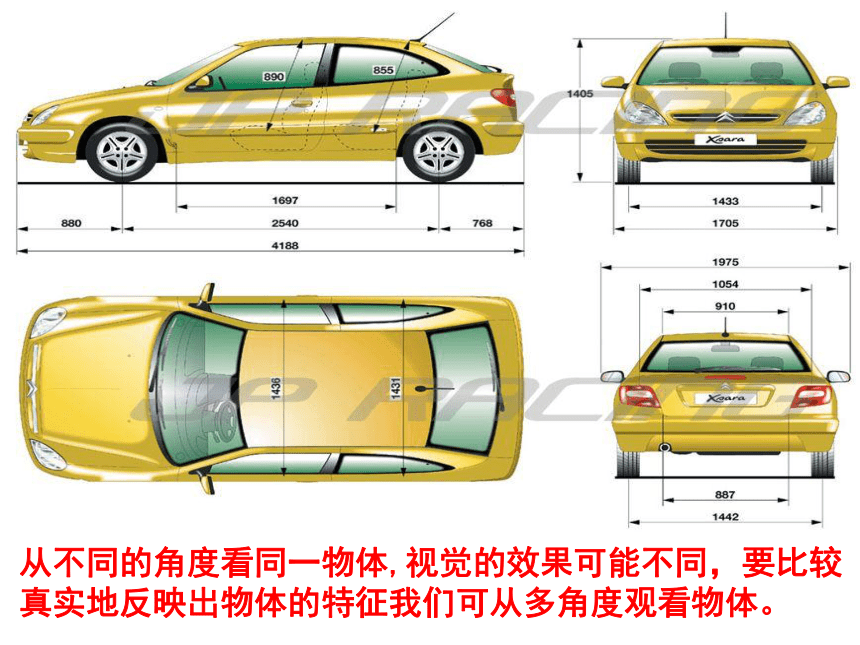
从不同的角度看同一物体,视觉的效果可能不同,要比较真实地反映出物体的特征我们可从多角度观看物体。
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
新课探究——空间几何体的三视图
把一个空间几何体投影到一个平面上,可以获得一个平面图形.
视图是指将物体按正投影向投影面投射所得到的图形.
从正面看到后面的视图叫做正视图,
从左面看到右面的视图叫做侧视图,
从上面看到下面的视图叫做俯视图。
三视图
新课探究——空间几何体的三视图
俯视图
正视图
俯视图
正视图
侧视图
侧视图
长
高
宽
高平齐
宽相等
根据长方体的模型,请你画出它的三视图,并观察三个图形之间的关系.
新课探究——空间几何体的三视图
长
高
宽
正视图:反映物体的高度和长度 .
侧视图:反映物体的高度和宽度 .
俯视图:反映物体的长度和宽度 .
三视图表达的意义:
三视图能反映物体真实的形状和长、宽、高.
新课探究——空间几何体的三视图
一般的,侧视图在正视图的右边,俯视图在正视图的下边.
一个几何体的正视图和侧视图的高度一样,俯视图和正视图的的长度一样,侧视图和俯视图的宽度一样.
俯视图
正视图
侧视图
新课探究——空间几何体的三视图
三视图的作图步骤:
1.确定三视图方向;
2.布置视图位置:正视图,侧视图,俯视图
要求:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方;
3.画图原则:正视长高,侧视宽高,俯视长宽.
新课探究——空间几何体的三视图
注:作图时能看见的轮廓线和棱用实线表示,
不能看见的用虚线表示.
下图所示的长方体和圆柱三视图是否正确
侧视图
正视图
俯视图
正视图
侧视图
俯视图
应用举例——简单几何体的三视图
主
左
俯
圆锥的三视图:
俯视图
正视图
侧视图
例1:分别画出下列几何体的三视图
应用举例
主
左
俯
圆台的三视图:
俯视图
侧视图
正视图
例1:分别画出下列几何体的三视图
应用举例
正四棱锥的三视图:
主
左
俯
应用举例
例1:分别画出下列几何体的三视图
正视图
侧视图
俯视图
正四面体
正四棱台
请试一试:
画出下列几何体的三视图!
课堂反馈——简单几何体的三视图
正四面体的三视图:
课堂反馈——简单几何体的三视图
正视图
侧视图
俯视图
正四棱台的三视图:
正视图
侧视图
俯视图
课堂反馈——简单几何体的三视图
正视图
侧视图
俯视图
变式:根据三视图找出对应的几何体
正六棱柱
课堂反馈——简单几何体的三视图
正六棱锥
变式:根据三视图找出对应的几何体
课堂反馈——简单几何体的三视图
例2:如图是一个倒置的四棱柱的两种摆放,试分别画出其三视图,并比较它们的异同.
应用举例——简单几何体的三视图
正视图
侧视图
俯视图
应用举例——简单几何体的三视图
正视图
侧视图
俯视图
能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.
应用举例——简单几何体的三视图
侧视图
正视图
俯视图
课堂反馈——简单几何体的三视图
变式:根据三视图找出对应的几何体
正视图
侧视图
俯视图
变式:根据三视图找出对应的几何体
课堂反馈——简单几何体的三视图
侧视图
俯视图
主视图
应用举例——简单组合体的三视图
例3:分别画出下列简单组合体的三视图
侧视图
俯视图
正视图
应用举例——简单组合体的三视图
例3:分别画出下列简单组合体的三视图
正视图
侧视图
俯视图
课堂反馈——简单组合体的三视图
变式:根据三视图找出对应的几何体
正视图
侧视图
俯视图
课堂反馈——简单组合体的三视图
变式:根据三视图找出对应的几何体
1.若某几何体的三视图如右图所示,请问这是什么几何体?
能力提升
正方体截去一个三棱锥
能力提升
1.某正三棱锥的正视图和俯视图如图所示,
则其侧视图面积为
【总一总★成竹在胸】
二、画几何体的三视图时,
能看得见的轮廓线或棱用实线表示,
不能看得见的轮廓线或棱用虚线表示。
一、三视图之间的投影规律:
正视图与俯视图------长对正。
正视图与侧视图------高平齐。
俯视图与侧视图------宽相等。
课时小结
学习目标:
1、了解中心投影和平行投影的原理;
2、能利用正投影绘制空间图形的三视图, 并根据所给的三视图识别该几何体;
3、能利用正投影绘制简单组合体的三视图,并根据所给的三视图说出该几何体由那些简单几何体构成。
请同学们看下面几个常见的自然现象,考虑它们是怎样得到的?
这种现象我们把它称为是投影
引入新课
投影是光线(投射线)通过物体,向选定的面(投影面)投射,并在该面上得到图形的方法.
通过观察和自己的认识 , 你是怎样来理解投影的含义的?
想一想?
引入新课
A
D
C
B
一、中心投影:
投射线
投影面
把光由一点向外散射形成的投影叫做中心投影。
特点:中心投影的投影大小与物体和投影面之间的距离有关。
引入新课
二、平行投影:
当把投影中心移到无穷远,在一束平行光线照射下形成的投影,叫做平行投影。
引入新课
二、平行投影:
正投影:投影方向垂直于投影面
的投影。
引入新课
二、平行投影:
斜投影:投影方向与投影面倾斜
的投影。
引入新课
投影
平行投影
中心投影
斜投影
正投影
本节主要学习利用正投影绘制空间图形的三视图,并能根据所给的三视图了解该空间图形的基本特征。
引入新课
猜猜他们是什么关系?
引入新课
看事物不能只看单方面
引入新课
从不同的角度看同一物体,视觉的效果可能不同,要比较真实地反映出物体的特征我们可从多角度观看物体。
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
新课探究——空间几何体的三视图
把一个空间几何体投影到一个平面上,可以获得一个平面图形.
视图是指将物体按正投影向投影面投射所得到的图形.
从正面看到后面的视图叫做正视图,
从左面看到右面的视图叫做侧视图,
从上面看到下面的视图叫做俯视图。
三视图
新课探究——空间几何体的三视图
俯视图
正视图
俯视图
正视图
侧视图
侧视图
长
高
宽
高平齐
宽相等
根据长方体的模型,请你画出它的三视图,并观察三个图形之间的关系.
新课探究——空间几何体的三视图
长
高
宽
正视图:反映物体的高度和长度 .
侧视图:反映物体的高度和宽度 .
俯视图:反映物体的长度和宽度 .
三视图表达的意义:
三视图能反映物体真实的形状和长、宽、高.
新课探究——空间几何体的三视图
一般的,侧视图在正视图的右边,俯视图在正视图的下边.
一个几何体的正视图和侧视图的高度一样,俯视图和正视图的的长度一样,侧视图和俯视图的宽度一样.
俯视图
正视图
侧视图
新课探究——空间几何体的三视图
三视图的作图步骤:
1.确定三视图方向;
2.布置视图位置:正视图,侧视图,俯视图
要求:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方;
3.画图原则:正视长高,侧视宽高,俯视长宽.
新课探究——空间几何体的三视图
注:作图时能看见的轮廓线和棱用实线表示,
不能看见的用虚线表示.
下图所示的长方体和圆柱三视图是否正确
侧视图
正视图
俯视图
正视图
侧视图
俯视图
应用举例——简单几何体的三视图
主
左
俯
圆锥的三视图:
俯视图
正视图
侧视图
例1:分别画出下列几何体的三视图
应用举例
主
左
俯
圆台的三视图:
俯视图
侧视图
正视图
例1:分别画出下列几何体的三视图
应用举例
正四棱锥的三视图:
主
左
俯
应用举例
例1:分别画出下列几何体的三视图
正视图
侧视图
俯视图
正四面体
正四棱台
请试一试:
画出下列几何体的三视图!
课堂反馈——简单几何体的三视图
正四面体的三视图:
课堂反馈——简单几何体的三视图
正视图
侧视图
俯视图
正四棱台的三视图:
正视图
侧视图
俯视图
课堂反馈——简单几何体的三视图
正视图
侧视图
俯视图
变式:根据三视图找出对应的几何体
正六棱柱
课堂反馈——简单几何体的三视图
正六棱锥
变式:根据三视图找出对应的几何体
课堂反馈——简单几何体的三视图
例2:如图是一个倒置的四棱柱的两种摆放,试分别画出其三视图,并比较它们的异同.
应用举例——简单几何体的三视图
正视图
侧视图
俯视图
应用举例——简单几何体的三视图
正视图
侧视图
俯视图
能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.
应用举例——简单几何体的三视图
侧视图
正视图
俯视图
课堂反馈——简单几何体的三视图
变式:根据三视图找出对应的几何体
正视图
侧视图
俯视图
变式:根据三视图找出对应的几何体
课堂反馈——简单几何体的三视图
侧视图
俯视图
主视图
应用举例——简单组合体的三视图
例3:分别画出下列简单组合体的三视图
侧视图
俯视图
正视图
应用举例——简单组合体的三视图
例3:分别画出下列简单组合体的三视图
正视图
侧视图
俯视图
课堂反馈——简单组合体的三视图
变式:根据三视图找出对应的几何体
正视图
侧视图
俯视图
课堂反馈——简单组合体的三视图
变式:根据三视图找出对应的几何体
1.若某几何体的三视图如右图所示,请问这是什么几何体?
能力提升
正方体截去一个三棱锥
能力提升
1.某正三棱锥的正视图和俯视图如图所示,
则其侧视图面积为
【总一总★成竹在胸】
二、画几何体的三视图时,
能看得见的轮廓线或棱用实线表示,
不能看得见的轮廓线或棱用虚线表示。
一、三视图之间的投影规律:
正视图与俯视图------长对正。
正视图与侧视图------高平齐。
俯视图与侧视图------宽相等。
课时小结
