1.2.1~1.2.2 中心投影与平行投影 空间几何体的三视图(课件)-2020-2021学年高一数学精品备课课件资源(人教A版必修2)33张PPT
文档属性
| 名称 | 1.2.1~1.2.2 中心投影与平行投影 空间几何体的三视图(课件)-2020-2021学年高一数学精品备课课件资源(人教A版必修2)33张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 13:39:47 | ||
图片预览










文档简介
§1.2.1 中心投影与平行投影
§1.2.2 空间几何体的三视图
人教A版数学必修2第一章《空间几何体》
【学习目标】
1.了解中心投影和平行投影的概念.
2.能画出简单空间图形(柱、锥、台、球及其组合体)的三视图.
3.能识别三视图所表示的立体模型.
自主预习
1
1.投影
(1)投影的定义
由于光的照射,在________物体后面的屏幕上可以留下这个物体的______,这种现象叫做投影.其中,我们把_____叫做投影线,把
的屏幕叫做投影面.
不透明
影子
光线
留下物体影子
(2)投影的分类
投影
定义
特征
分类
中心投影
光由 向外散射形成的投影
投影线__________
?
平行投影
在一束 照射下形成的投影
投影线_____
和_______
一点
平行光线
交于一点
平行
正投影
斜投影
(3)当图形中的直线或线段不平行于投影线时,平行投影都具有下述性质:
①直线或线段的平行投影_______________ _;②平行直线的平行投影是 ;③平行于投影面的线段,它的投影与这条线段___________;④与投影面平行的平面图形,它的投影与这个图形_____;⑤在同一直线或平行直线上,两条线段平行投影的比等于______________.
仍是直线或线段
平行或重合的直线
平行且等长
全等
这两条线段的比
(1)定义:光线从几何体的___面向___面正投影,得到投影图,这种投影图叫做几何体的正视图;光线从几何体的___面向___面正投影,得到投影图,这种投影图叫做几何体的侧视图;光线从几何体的___面向___面正投影,得到投影图,这种投影图叫做几何体的俯视图.几何体的正视图、侧视图、俯视图统称为几何体的_________,三视图是正投影.
2.三视图
前
后
左
右
上
下
三视图
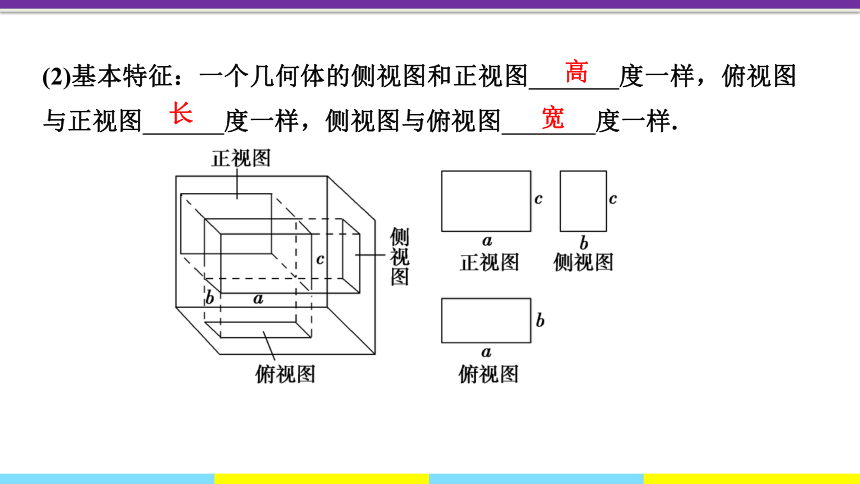
(2)基本特征:一个几何体的侧视图和正视图 度一样,俯视图与正视图 度一样,侧视图与俯视图 度一样.
高
长
宽
宽相等:俯视图与侧视图的宽度应相等.
可概括为:正、俯视图——长对正;正、侧视图——高平齐;俯、侧视图——宽相等.
【例2】下列说法中:
①平行投影的投影线互相平行,中心投影的投影线相交于一点;②空间图形经过中心投影后,直线还是直线,但平行线可能变成了相交的直线;③两条相交直线的平行投影是两条相交直线.其中正确的个数为( )
A.0 B.1 C.2 D.3
【解析】由平行投影和中心投影的定义可知①正确;空间图形经过中心投影后,直线可能变成直线,也可能变成一个点,如当投影中心在直线上时,投影为点;平行线有可能变成相交线,如照片中由近到远物体之间的距离越来越近,最后相交于一点,②不正确;两条相交直线的平行投影是两条相交直线或一条直线,③不正确.
【答案】B
题型二 三视图的识别
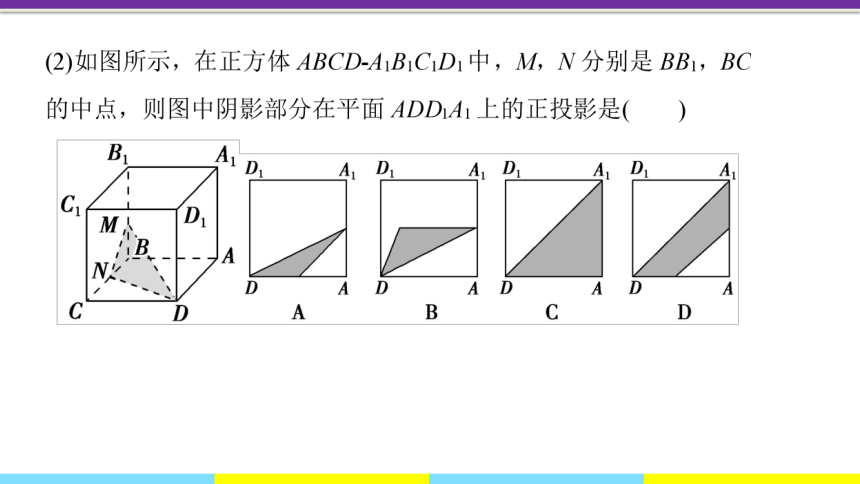
【例3】如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.②③ D.②④
【解析】在各自的三视图中,①正方体的三个视图都相同;
②圆锥有两个视图相同;
③三棱台的三个视图都不同;
④正四棱锥有两个视图相同.
【例4】已知三棱柱ABC-A1B1C1,如图所示,则其三视图为( )
【解析】其正视图为矩形,侧视图为三角形,俯视图中棱CC1可见,为实线,只有A符合.
题型三 画几何体的三视图
【例5】(1)画出如图所示的几何体(正棱锥)的三视图.
【解析】正四棱锥的三视图如图所示,
(2)画出如图所示的组合体的三视图.
解
【例8】根据三视图(如图所示)想象物体原形,指出其结构特征并画出物体的实物草图.
【解析】该几何体是由一个圆柱和一个底面为正方形的长方体组合而成,且圆柱下底面圆的直径等于长方体底面正方形的边长,其草图如图所示.
课堂练习
1.某几何体如图所示,则其主视图和左视图是( )
【解析】显然主视图是矩形,其左上方至右下方有一实线对角线.左视图也是矩形,其左上方至右下方有一虚线对角线,只有B符合,所以选B.
【答案】B
2.若一个三棱柱的三视图如图所示,其俯视图为正三角形,则这个三棱柱的高和底面边长分别为( )
?
【答案】D
3.图中所示立体图形,都是由相同的小正方体拼成的.
(1)图①的主视图与图②的________相同;
(2)图③的主视图与图④的主视图________.
【答案】(1)俯视图 (2)不同
课堂小结
1.三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线,画几何体三视图的要求是正视图、俯视图长对正,正视图、侧视图高平齐,俯视图、侧视图宽相等,前后对应,画出的三视图要检验是否符合“长对正、高平齐、宽相等”的基本特征.
§1.2.2 空间几何体的三视图
人教A版数学必修2第一章《空间几何体》
【学习目标】
1.了解中心投影和平行投影的概念.
2.能画出简单空间图形(柱、锥、台、球及其组合体)的三视图.
3.能识别三视图所表示的立体模型.
自主预习
1
1.投影
(1)投影的定义
由于光的照射,在________物体后面的屏幕上可以留下这个物体的______,这种现象叫做投影.其中,我们把_____叫做投影线,把
的屏幕叫做投影面.
不透明
影子
光线
留下物体影子
(2)投影的分类
投影
定义
特征
分类
中心投影
光由 向外散射形成的投影
投影线__________
?
平行投影
在一束 照射下形成的投影
投影线_____
和_______
一点
平行光线
交于一点
平行
正投影
斜投影
(3)当图形中的直线或线段不平行于投影线时,平行投影都具有下述性质:
①直线或线段的平行投影_______________ _;②平行直线的平行投影是 ;③平行于投影面的线段,它的投影与这条线段___________;④与投影面平行的平面图形,它的投影与这个图形_____;⑤在同一直线或平行直线上,两条线段平行投影的比等于______________.
仍是直线或线段
平行或重合的直线
平行且等长
全等
这两条线段的比
(1)定义:光线从几何体的___面向___面正投影,得到投影图,这种投影图叫做几何体的正视图;光线从几何体的___面向___面正投影,得到投影图,这种投影图叫做几何体的侧视图;光线从几何体的___面向___面正投影,得到投影图,这种投影图叫做几何体的俯视图.几何体的正视图、侧视图、俯视图统称为几何体的_________,三视图是正投影.
2.三视图
前
后
左
右
上
下
三视图
(2)基本特征:一个几何体的侧视图和正视图 度一样,俯视图与正视图 度一样,侧视图与俯视图 度一样.
高
长
宽
宽相等:俯视图与侧视图的宽度应相等.
可概括为:正、俯视图——长对正;正、侧视图——高平齐;俯、侧视图——宽相等.
【例2】下列说法中:
①平行投影的投影线互相平行,中心投影的投影线相交于一点;②空间图形经过中心投影后,直线还是直线,但平行线可能变成了相交的直线;③两条相交直线的平行投影是两条相交直线.其中正确的个数为( )
A.0 B.1 C.2 D.3
【解析】由平行投影和中心投影的定义可知①正确;空间图形经过中心投影后,直线可能变成直线,也可能变成一个点,如当投影中心在直线上时,投影为点;平行线有可能变成相交线,如照片中由近到远物体之间的距离越来越近,最后相交于一点,②不正确;两条相交直线的平行投影是两条相交直线或一条直线,③不正确.
【答案】B
题型二 三视图的识别
【例3】如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.②③ D.②④
【解析】在各自的三视图中,①正方体的三个视图都相同;
②圆锥有两个视图相同;
③三棱台的三个视图都不同;
④正四棱锥有两个视图相同.
【例4】已知三棱柱ABC-A1B1C1,如图所示,则其三视图为( )
【解析】其正视图为矩形,侧视图为三角形,俯视图中棱CC1可见,为实线,只有A符合.
题型三 画几何体的三视图
【例5】(1)画出如图所示的几何体(正棱锥)的三视图.
【解析】正四棱锥的三视图如图所示,
(2)画出如图所示的组合体的三视图.
解
【例8】根据三视图(如图所示)想象物体原形,指出其结构特征并画出物体的实物草图.
【解析】该几何体是由一个圆柱和一个底面为正方形的长方体组合而成,且圆柱下底面圆的直径等于长方体底面正方形的边长,其草图如图所示.
课堂练习
1.某几何体如图所示,则其主视图和左视图是( )
【解析】显然主视图是矩形,其左上方至右下方有一实线对角线.左视图也是矩形,其左上方至右下方有一虚线对角线,只有B符合,所以选B.
【答案】B
2.若一个三棱柱的三视图如图所示,其俯视图为正三角形,则这个三棱柱的高和底面边长分别为( )
?
【答案】D
3.图中所示立体图形,都是由相同的小正方体拼成的.
(1)图①的主视图与图②的________相同;
(2)图③的主视图与图④的主视图________.
【答案】(1)俯视图 (2)不同
课堂小结
1.三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线,画几何体三视图的要求是正视图、俯视图长对正,正视图、侧视图高平齐,俯视图、侧视图宽相等,前后对应,画出的三视图要检验是否符合“长对正、高平齐、宽相等”的基本特征.
