华师大版数学七年级上2.9.3有理数的乘法分配律课件
文档属性
| 名称 | 华师大版数学七年级上2.9.3有理数的乘法分配律课件 |  | |
| 格式 | rar | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-16 06:50:54 | ||
图片预览








文档简介
(共24张PPT)
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
(第三课时)
教学目标
1.使学生掌握乘法的分配律,并能灵活的运用
2.使学生掌握有理数乘法的运算律,并利用运算律简化乘法运算。
3.使学生掌握一些运算方法,培养学生运算能力。
教学重点、难点
重点:乘法的运算律和运算能力的提高。
难点:运算能力的提高。
一、温故知新、引入课题
1、叙述有理数乘法法则和乘法的交换律、结合律
2.计算:
(1)8+5×(―4); (2)(―3)×(―7)―9×(―6)?
想一想,做一做
解:原式=8+(―20) (先乘后加) 解:原式=21―(―54)(先乘后减)
=―12; =75
在有理数乘法中,首先要掌握积的符号法则,当符号确定后又归结到小学数学的乘法运算上,四则运算顺序也同小学一样,先进行第二级运算,再进行第一级运算,若有括号先算括号里的式子。?
在有理数的乘法
的计算中注意
在小学里,我们曾经学过乘法的分配律,如:
想一想
这个运算律在有理数乘 法运算中也是成立的吗?
任意选择三个有理数(至少有一个是负数),分别填入下列□、○
和◇内,并比较两个算式的运算结果。
□ ×( ○ + ◇) 和 □×○ + □×◇
计算:
(1) 6×(2-3)
做一做,想一想
(2)6 ×2 -6 ×3
=6 ×(-1)
=-6
=12-18
=-6
聪明的你通过计算
发现了什么呢?
把规律总结一下
乘法的分配律
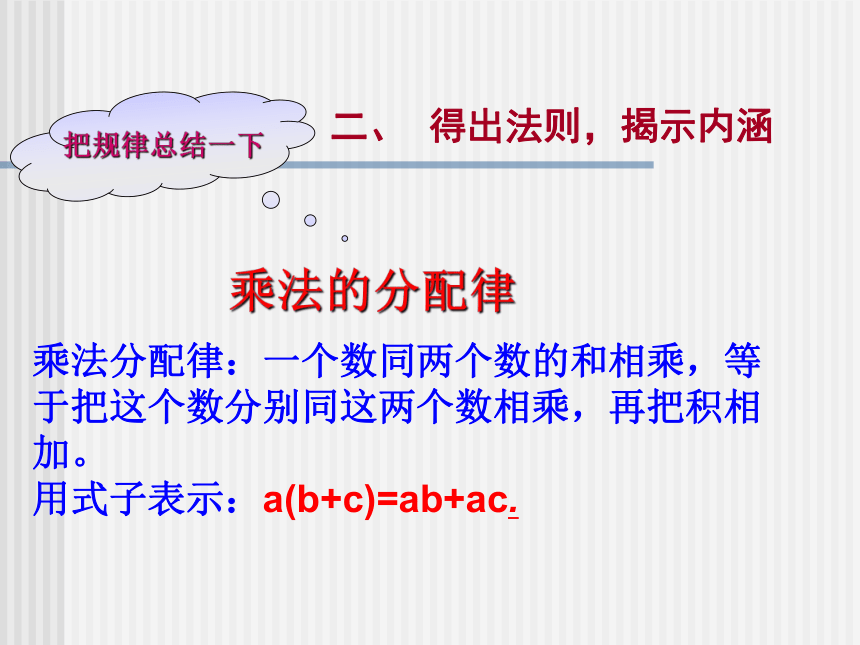
二、 得出法则,揭示内涵
乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
用式子表示:a(b+c)=ab+ac.
例1.计算 (1)
分析:可先把括号内计算,但分数的计算麻烦
解:
三 例题示范,初步运用
(2) 4.98×(-5)
解:4.98 ×(-5)
=(5-0.02) ×(-5)
= 5×(-5)-0.02 ×(-5)
=-25+0.1
=-24.9
例2 计算:
(1)
解:
(2)
解:
以上的例题你发现了什么?
适当的应用运算律,可使运算简便;有时需要先把算式变形,才能用分配律;有时也可以反用分配律
1.下列各式中用了哪条运算律?如何用字母表示?
1)(-4)×8 = 8 ×(-4)
2)[(-8)+5]+(-4)=(-8)+[5+(-4)]
3)(-6)×[ - +(- -)]=(-6)× - +(-6)×(- - )
4)[29×(- - )] ×(-12)=29 ×[(- - ) ×(-12)]
5)(-8)+(-9)=(-9)+(-8)
乘法交换律:a×b=b×a
分配律:a×(b+c)=a×b+b×c
乘法结合律(a×b)×c=a×(b×c)
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
2
3
1
2
1
2
2
3
5
6
5
6
四、分层练习,形成能力
__ __ __
看一看,错在哪里?
正确解法:
_____ ______ ______ _____
提别提醒:不要漏掉符号,不要漏乘
1.(-8)×(-12)×(-0.125)×(- )
×(-0.1)
计算:
考虑如何用简便方法计算下面的问题:
4×(-3)+3 ×(-3)-2 ×(-3)+7 ×(-3)
分析:1 、按照一般计算规则,要先做乘法 (4次)再做加减法(3次),共需要进行
7次计算。
2、注意到问题中的乘法都有公共的因数(-3),可以将分配律反过来利用(逆用)。
4×(-3)+3 ×(-3)-2 ×(-3)+7 ×(-3)
解:原式= ( 4 + 3 – 2 + 7 ) ×( -3 )
= 12 × (-3)
= -36
另解: 原式= -12 + (-9) + 6 - 21
= - (12 + 9 + 21) + 6
= -42 + 6
= -36
这种方法只需做3次加减法与1次乘法, 共需进行4次计算.
这种方法需先做4次乘法再做3次加减法, 共需进行7次计算.
例如: (-23)×25-6×25+18×25+25
用简便方法计算:
解: 原式=(-23-6+18+1) ×25
=(-10) ×25
=-250
归纳:
我们将分配律的反过来利用(逆用)在解题中,可以简化计算,减少计算量,提高正确律.
五、回顾小结,
突出重点
1.乘法的分配律。
2.在运用乘法分配律时应注意的问题。
3.乘法分配律的逆用。
本节课里我的收获是……
1.课本P57页,习题2.9 4
2.预习课本P58—P61
六、布置作业,引导预习
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
(第三课时)
教学目标
1.使学生掌握乘法的分配律,并能灵活的运用
2.使学生掌握有理数乘法的运算律,并利用运算律简化乘法运算。
3.使学生掌握一些运算方法,培养学生运算能力。
教学重点、难点
重点:乘法的运算律和运算能力的提高。
难点:运算能力的提高。
一、温故知新、引入课题
1、叙述有理数乘法法则和乘法的交换律、结合律
2.计算:
(1)8+5×(―4); (2)(―3)×(―7)―9×(―6)?
想一想,做一做
解:原式=8+(―20) (先乘后加) 解:原式=21―(―54)(先乘后减)
=―12; =75
在有理数乘法中,首先要掌握积的符号法则,当符号确定后又归结到小学数学的乘法运算上,四则运算顺序也同小学一样,先进行第二级运算,再进行第一级运算,若有括号先算括号里的式子。?
在有理数的乘法
的计算中注意
在小学里,我们曾经学过乘法的分配律,如:
想一想
这个运算律在有理数乘 法运算中也是成立的吗?
任意选择三个有理数(至少有一个是负数),分别填入下列□、○
和◇内,并比较两个算式的运算结果。
□ ×( ○ + ◇) 和 □×○ + □×◇
计算:
(1) 6×(2-3)
做一做,想一想
(2)6 ×2 -6 ×3
=6 ×(-1)
=-6
=12-18
=-6
聪明的你通过计算
发现了什么呢?
把规律总结一下
乘法的分配律
二、 得出法则,揭示内涵
乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
用式子表示:a(b+c)=ab+ac.
例1.计算 (1)
分析:可先把括号内计算,但分数的计算麻烦
解:
三 例题示范,初步运用
(2) 4.98×(-5)
解:4.98 ×(-5)
=(5-0.02) ×(-5)
= 5×(-5)-0.02 ×(-5)
=-25+0.1
=-24.9
例2 计算:
(1)
解:
(2)
解:
以上的例题你发现了什么?
适当的应用运算律,可使运算简便;有时需要先把算式变形,才能用分配律;有时也可以反用分配律
1.下列各式中用了哪条运算律?如何用字母表示?
1)(-4)×8 = 8 ×(-4)
2)[(-8)+5]+(-4)=(-8)+[5+(-4)]
3)(-6)×[ - +(- -)]=(-6)× - +(-6)×(- - )
4)[29×(- - )] ×(-12)=29 ×[(- - ) ×(-12)]
5)(-8)+(-9)=(-9)+(-8)
乘法交换律:a×b=b×a
分配律:a×(b+c)=a×b+b×c
乘法结合律(a×b)×c=a×(b×c)
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
2
3
1
2
1
2
2
3
5
6
5
6
四、分层练习,形成能力
__ __ __
看一看,错在哪里?
正确解法:
_____ ______ ______ _____
提别提醒:不要漏掉符号,不要漏乘
1.(-8)×(-12)×(-0.125)×(- )
×(-0.1)
计算:
考虑如何用简便方法计算下面的问题:
4×(-3)+3 ×(-3)-2 ×(-3)+7 ×(-3)
分析:1 、按照一般计算规则,要先做乘法 (4次)再做加减法(3次),共需要进行
7次计算。
2、注意到问题中的乘法都有公共的因数(-3),可以将分配律反过来利用(逆用)。
4×(-3)+3 ×(-3)-2 ×(-3)+7 ×(-3)
解:原式= ( 4 + 3 – 2 + 7 ) ×( -3 )
= 12 × (-3)
= -36
另解: 原式= -12 + (-9) + 6 - 21
= - (12 + 9 + 21) + 6
= -42 + 6
= -36
这种方法只需做3次加减法与1次乘法, 共需进行4次计算.
这种方法需先做4次乘法再做3次加减法, 共需进行7次计算.
例如: (-23)×25-6×25+18×25+25
用简便方法计算:
解: 原式=(-23-6+18+1) ×25
=(-10) ×25
=-250
归纳:
我们将分配律的反过来利用(逆用)在解题中,可以简化计算,减少计算量,提高正确律.
五、回顾小结,
突出重点
1.乘法的分配律。
2.在运用乘法分配律时应注意的问题。
3.乘法分配律的逆用。
本节课里我的收获是……
1.课本P57页,习题2.9 4
2.预习课本P58—P61
六、布置作业,引导预习
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
