青岛版数学九年级上4.6 圆与圆的位置关系课件
文档属性
| 名称 | 青岛版数学九年级上4.6 圆与圆的位置关系课件 |
|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-16 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
圆
与
圆
的 位 置 关 系
九年级数学(上)第四章: 对圆的进一步认识
实验中学 冯丽丽老师
奥运会会徽
日全食
按钮
活动 一
活动 二
1、亲自动手实验
实验步骤与目的:
在两张透明纸上画出两个半径不同的圆,把两张纸叠合在一起,固定其中一张
而移动另一张,请观察圆与圆有几种位置关系?你能画出几种不同的位置关系
吗?每种位置关系中两圆有多少公共点?
2、演示圆与圆相对运动
驶向胜利彼岸
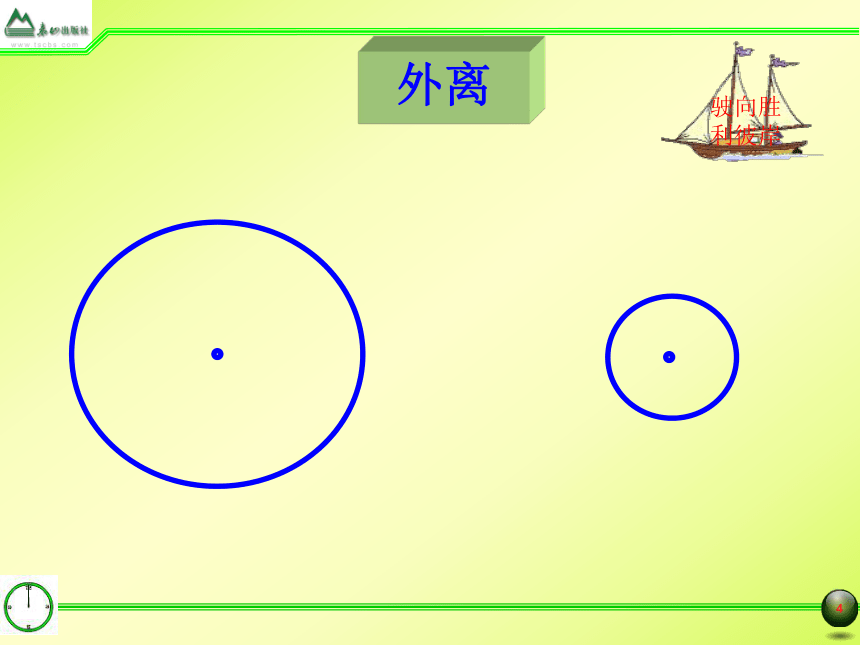
外离
驶向胜利彼岸
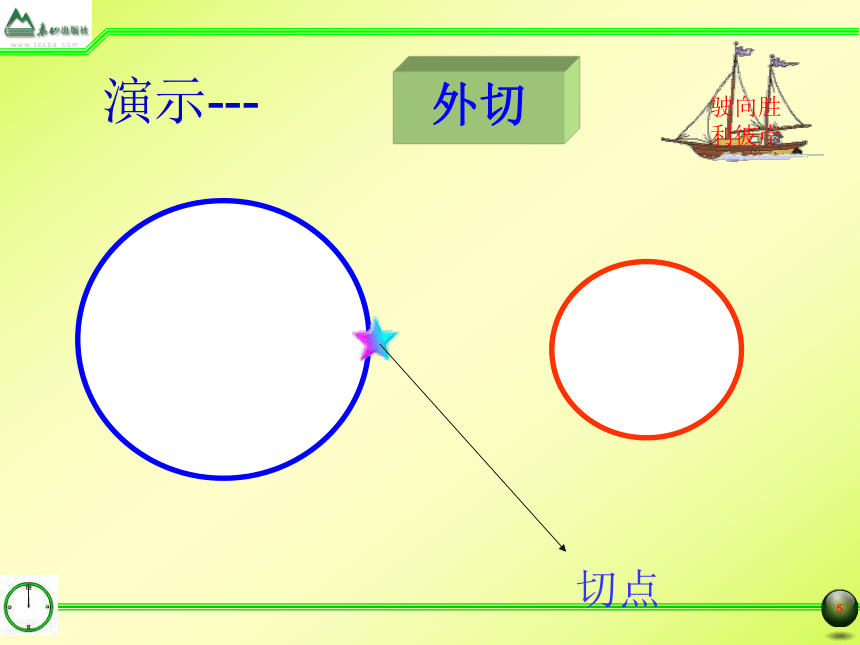
外切
演示---
切点
驶向胜利彼岸
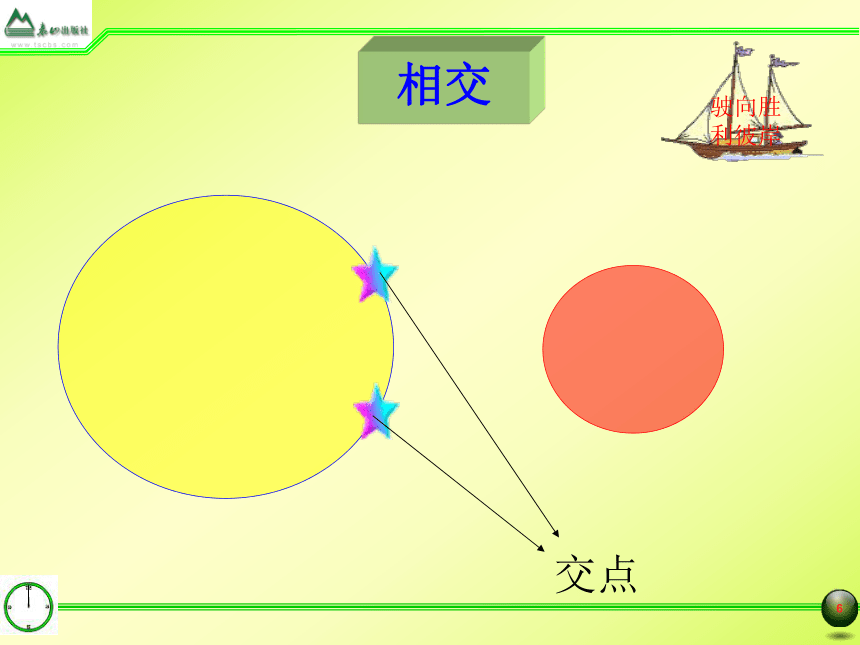
相交
交点
驶向胜利彼岸
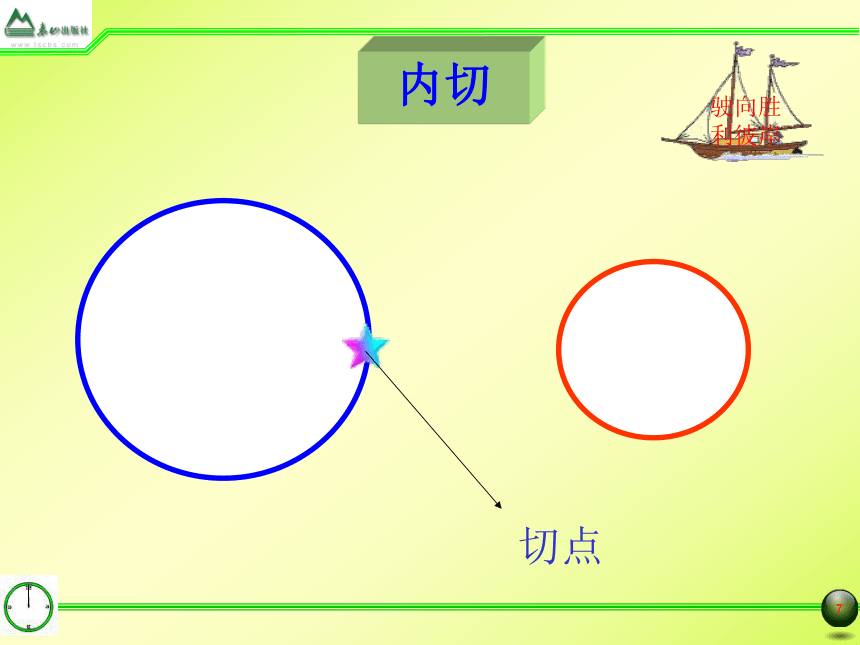
内切
切点
驶向胜利彼岸
内含
驶向胜利彼岸
同心圆
驶向胜利彼岸
相 离
相 切
相 交
外离
内含
外切
内切
你能再举出一些表示生活中两圆不同的位置关系实例吗?
活动三
活动四
定理探索
演示
发现规律
1、两圆的位置关系与半径和差有关
R-r
内切
R+r
外切
口决:和差切,交中间,内含外离在两边
内含
相交
外离
驶向胜利彼岸
1、⊙01和⊙02的半径分别为3cm和4cm,设
(1) 0102=8cm (2) 0102=7cm
(3) 0102=5cm (4) 0102=1cm
(5) 0102=0.5cm (6) 01和02重合
⊙0和⊙02的位置关系怎样
练习
(2)两圆外切
(3)两圆相交
(4)两圆内切
(5)两圆内含
(6)两圆同心
答: (1)两圆相离
例1:如图⊙O的半径为4cm,点P是⊙O外一点,OP=6cm
求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P 的半径是多少
(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少
解:(1)设⊙O与⊙P外切
于点A,则 PA=OP-OA
∴ PA=2 cm
(2)设⊙O与⊙P内切
于点B,则 PB=OP+OB
∴ PB=10 cm.
0
P
A
B
.
.
请看课本:以P为圆心作⊙P与⊙O相切?
定圆0的半径是4cm,动圆P的半径是1cm,
(1) 设⊙ P和⊙ 0相外切,那么点P与点O的距离
是多少 点P可以在什么样的线上运动
(2) 设⊙ P 和 ⊙O 相内切,情况又怎样
(1) 解:∵⊙0和⊙P相外切
∴OP= R + r
∴OP=5cm
∴ P点在以O点为圆心,以5cm
为半径的圆上运动
讨论思考
(2) 解: ∵⊙0和⊙P相内切
∴ OP=R-r
∴OP=3cm
∴ P点在以O点为圆心,以3cm
为半径的圆上运动
课堂小结
外离
外切
相交
内切
内含
0
1
2
1
0
d>R+r
d=R+r
R-rd=R-r
0 ≤ d公共点
圆心距和半径的关系
两圆位置
一圆在另一
圆的外部
一圆在另一
圆的外部
两圆相交
一圆在另一
圆的内部
一圆在另一
圆的内部
名称
驶向胜利彼岸
布置作业
1、将例题增加一问:以点P为圆心,作圆P与圆O外离,相交或内含,圆P的半径各是多少?
2、将讨论作变式训练: ⊙O1半径为2,⊙O2半径为1,如果⊙O1固定,⊙O2 绕⊙O1滚动一周,且⊙O2不停自转,当⊙O2回到原来位置,⊙O2转了几周?
驶向胜利彼岸
驶向胜利彼岸
圆
与
圆
的 位 置 关 系
九年级数学(上)第四章: 对圆的进一步认识
实验中学 冯丽丽老师
奥运会会徽
日全食
按钮
活动 一
活动 二
1、亲自动手实验
实验步骤与目的:
在两张透明纸上画出两个半径不同的圆,把两张纸叠合在一起,固定其中一张
而移动另一张,请观察圆与圆有几种位置关系?你能画出几种不同的位置关系
吗?每种位置关系中两圆有多少公共点?
2、演示圆与圆相对运动
驶向胜利彼岸
外离
驶向胜利彼岸
外切
演示---
切点
驶向胜利彼岸
相交
交点
驶向胜利彼岸
内切
切点
驶向胜利彼岸
内含
驶向胜利彼岸
同心圆
驶向胜利彼岸
相 离
相 切
相 交
外离
内含
外切
内切
你能再举出一些表示生活中两圆不同的位置关系实例吗?
活动三
活动四
定理探索
演示
发现规律
1、两圆的位置关系与半径和差有关
R-r
内切
R+r
外切
口决:和差切,交中间,内含外离在两边
内含
相交
外离
驶向胜利彼岸
1、⊙01和⊙02的半径分别为3cm和4cm,设
(1) 0102=8cm (2) 0102=7cm
(3) 0102=5cm (4) 0102=1cm
(5) 0102=0.5cm (6) 01和02重合
⊙0和⊙02的位置关系怎样
练习
(2)两圆外切
(3)两圆相交
(4)两圆内切
(5)两圆内含
(6)两圆同心
答: (1)两圆相离
例1:如图⊙O的半径为4cm,点P是⊙O外一点,OP=6cm
求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P 的半径是多少
(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少
解:(1)设⊙O与⊙P外切
于点A,则 PA=OP-OA
∴ PA=2 cm
(2)设⊙O与⊙P内切
于点B,则 PB=OP+OB
∴ PB=10 cm.
0
P
A
B
.
.
请看课本:以P为圆心作⊙P与⊙O相切?
定圆0的半径是4cm,动圆P的半径是1cm,
(1) 设⊙ P和⊙ 0相外切,那么点P与点O的距离
是多少 点P可以在什么样的线上运动
(2) 设⊙ P 和 ⊙O 相内切,情况又怎样
(1) 解:∵⊙0和⊙P相外切
∴OP= R + r
∴OP=5cm
∴ P点在以O点为圆心,以5cm
为半径的圆上运动
讨论思考
(2) 解: ∵⊙0和⊙P相内切
∴ OP=R-r
∴OP=3cm
∴ P点在以O点为圆心,以3cm
为半径的圆上运动
课堂小结
外离
外切
相交
内切
内含
0
1
2
1
0
d>R+r
d=R+r
R-r
0 ≤ d
圆心距和半径的关系
两圆位置
一圆在另一
圆的外部
一圆在另一
圆的外部
两圆相交
一圆在另一
圆的内部
一圆在另一
圆的内部
名称
驶向胜利彼岸
布置作业
1、将例题增加一问:以点P为圆心,作圆P与圆O外离,相交或内含,圆P的半径各是多少?
2、将讨论作变式训练: ⊙O1半径为2,⊙O2半径为1,如果⊙O1固定,⊙O2 绕⊙O1滚动一周,且⊙O2不停自转,当⊙O2回到原来位置,⊙O2转了几周?
驶向胜利彼岸
驶向胜利彼岸
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
