2020年河北省中考——外心、内心备考专题学案
文档属性
| 名称 | 2020年河北省中考——外心、内心备考专题学案 |  | |
| 格式 | zip | ||
| 文件大小 | 354.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 23:46:43 | ||
图片预览

文档简介
2020年河北省中考外心、内心备考
2016年的第9题就是由2010年的第6题改编而来。
2018年的第15题和2019年的第23题都考的内心,都源自课本。
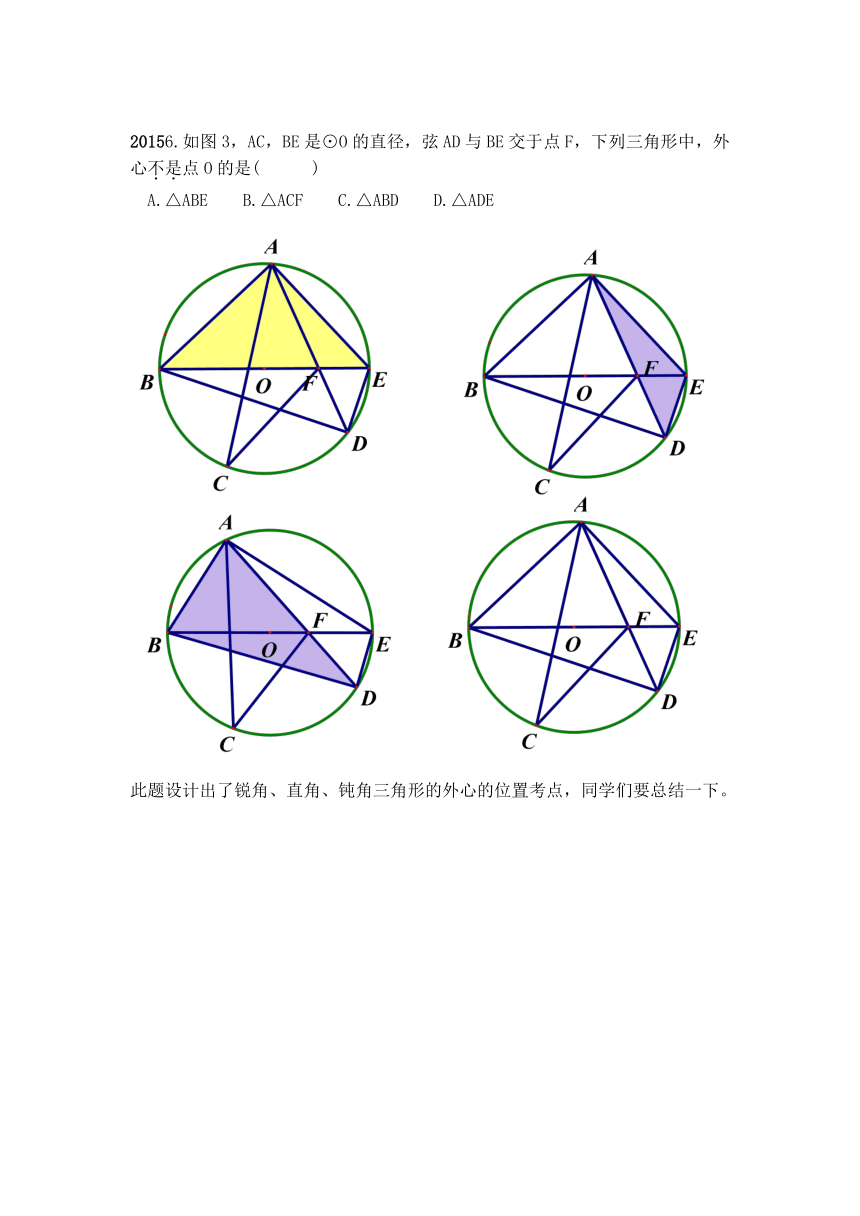
外心:三角形外接圆的圆心(三角形三边的垂直平分线的交点)。圆和三角形的位置关系是圆在三角形的外部,所以叫外接圆的圆心,简称外心。
外心的特点:锐角三角形的外心在三角形的内部,直角三角形的外心在斜边中点,钝角三角形的外心在三角形外部,并且在最大的角所对的方向。
现在分析河北省近几年外心考点。
2010年是河北省第一考外心,虽然没有出现外心这个词,但是连接A、B、C三点,形成△ABC,
△ABC是钝角三角形,找三角形的外心,找任意两个边的垂直平分线的交点即可。首先画出AB边的垂直平分线,可以确实外心为Q点或M点,再画出BC的垂直平分线,交点为Q.
20106.如图3,在5×5正方形网格中,一条圆弧经过A,B,C三点,
那么这条圆弧所在圆的圆心是(
)A.点P
B.点Q
C.点R
D.点M
分析:这是河北省刚开始考尺规作图时设计的此题,考到了线段垂直平分线的画法,钝角三角形的外心。
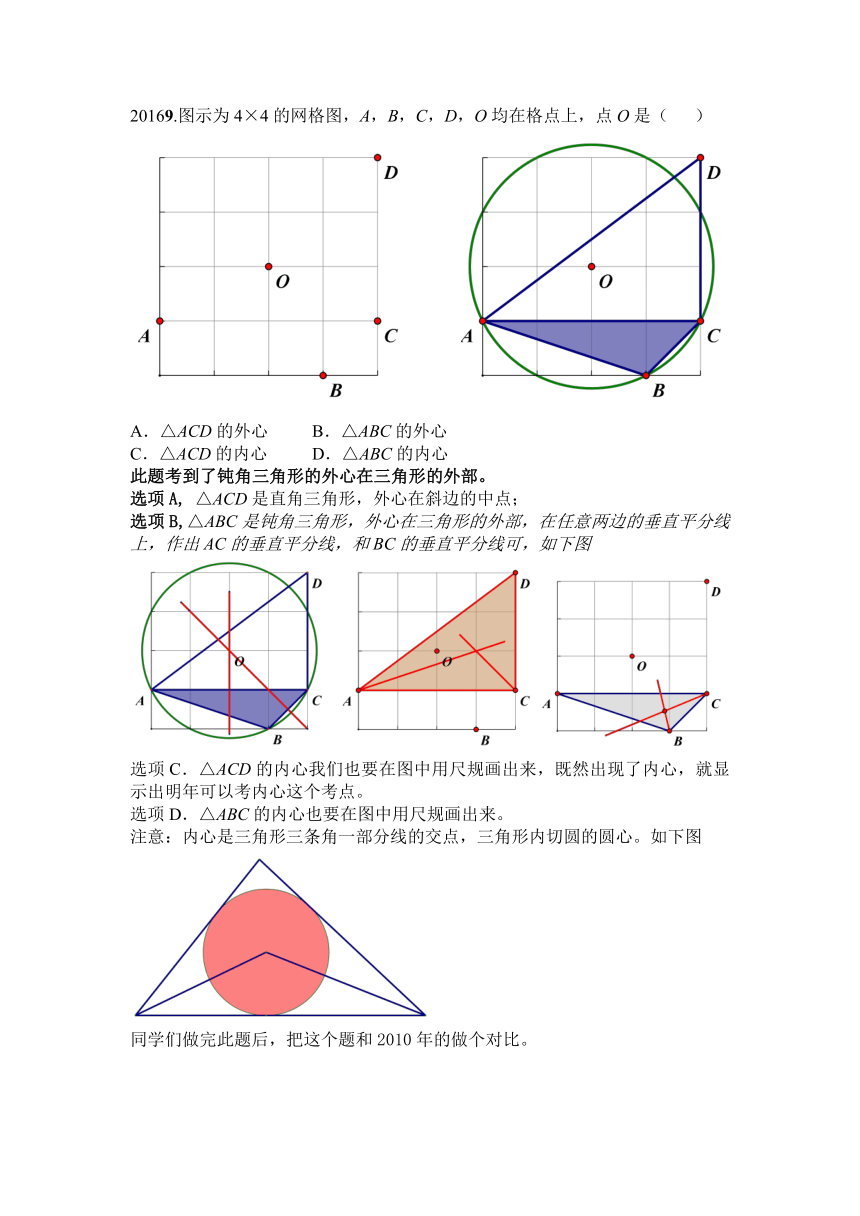
20156.如图3,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是(
)
A.△ABE
B.△ACF
C.△ABD
D.△ADE
此题设计出了锐角、直角、钝角三角形的外心的位置考点,同学们要总结一下。
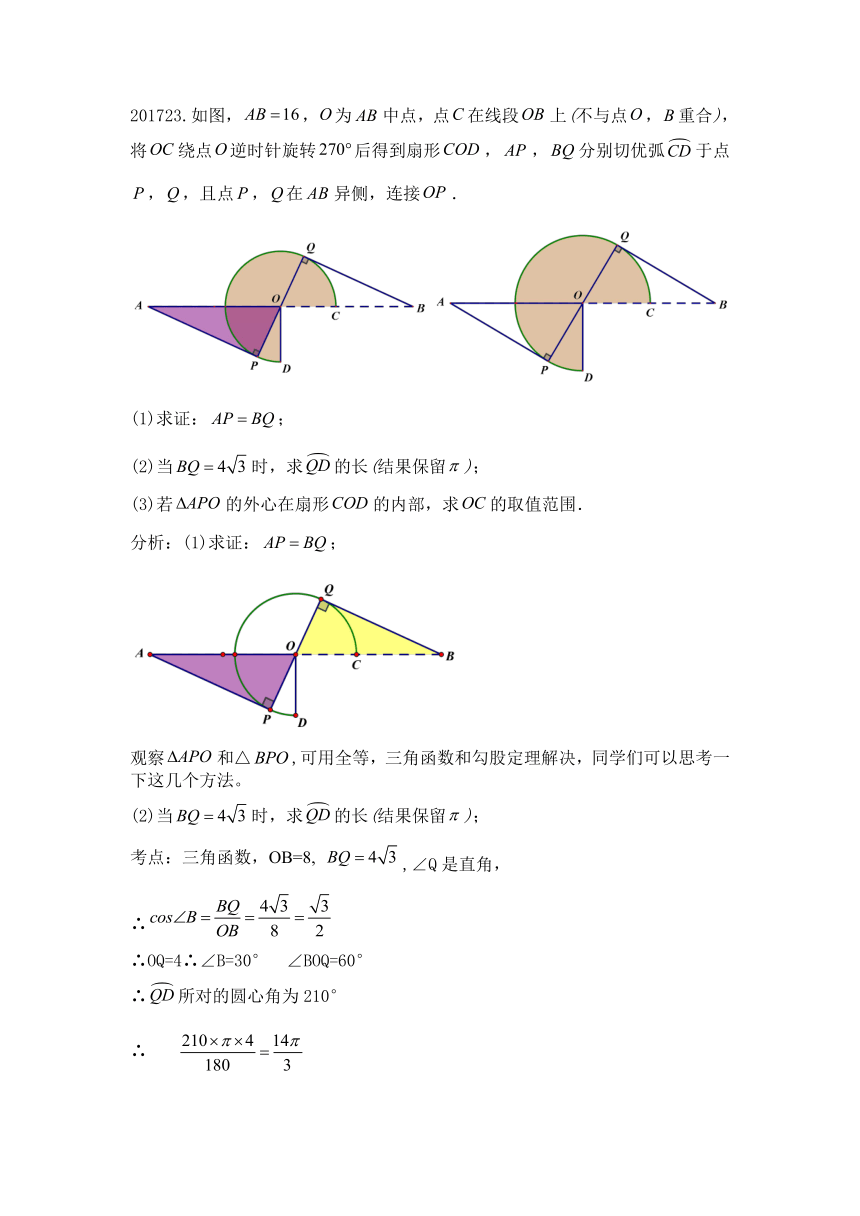
20169.图示为4×4的网格图,A,B,C,D,O均在格点上,点O是(
)
A.△ACD的外心
B.△ABC的外心
C.△ACD的内心
D.△ABC的内心
此题考到了钝角三角形的外心在三角形的外部。
选项A,
△ACD是直角三角形,外心在斜边的中点;
选项B,△ABC是钝角三角形,外心在三角形的外部,在任意两边的垂直平分线上,作出AC的垂直平分线,和BC的垂直平分线可,如下图
选项C.△ACD的内心我们也要在图中用尺规画出来,既然出现了内心,就显示出明年可以考内心这个考点。
选项D.△ABC的内心也要在图中用尺规画出来。
注意:内心是三角形三条角一部分线的交点,三角形内切圆的圆心。如下图
同学们做完此题后,把这个题和2010年的做个对比。
201723.如图,,为中点,点在线段上(不与点,重合),将绕点逆时针旋转后得到扇形,,分别切优弧于点,,且点,在异侧,连接.
(1)求证:;
(2)当时,求的长(结果保留);
(3)若的外心在扇形的内部,求的取值范围.
分析:(1)求证:;
观察和△,可用全等,三角函数和勾股定理解决,同学们可以思考一
下这几个方法。
(2)当时,求的长(结果保留);
考点:三角函数,OB=8,
,∠Q是直角,
∴
∴OQ=4∴∠B=30°
∠BOQ=60°
∴所对的圆心角为210°
∴
(3)若的外心在扇形的内部,求的取值范围.
锐角三角形的外心在三角形的内部。
思考:当OC=8时,点P与点A重合,不存在。此处应用心思考,2019年考内心时就涉及到了两点重合时产情况。所以,动点问题,我们一定要化动为静,先找到起点、终点、及中间的特殊点。思考时,不要漏。
201823
如图13,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意一点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM?△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
解:(1)
∵点P为AB的中点,∴
AP=BP.
在△APM和△BPN中,
∴△APM和△BPN(ASA)
(2)由(1),得△APM和△BPN,∴PM=PN.∴2PN=MN.
又∵MN=2BN,
∴PN=BN.
∴.
(3)
.
【提示:外心所在的位置与三角形的形状有关,锐角三角形的外心在三角形内部,直角三角形的外心在斜边中点处,钝角三角形的外心在三角形的外部。只需求出△BPN为锐角三角形时,的取值范围。】
201815内心
内心是三角形三条角一部分线的交点,三角形内切圆的圆心。如下图
下面这个题源自课本(人教版八上)
如图点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使共顶点与I重合,则图中阴影部分的周长为(
)
A.4.5
B.4
C.3
D.2
三角形的内心是任意两条角平分线的交点,平移产生平行。
角平分线+平行,产生等腰三角形。
2019年第10题,用尺规作图作出三角形的外心,符合物极必反的规律。三角形的外心连续考了好几年了,锐角三角形、钝角三角形、直角三角形都考过了。很多朋友设计了好多高难度的外心的题,进行中考前模拟训练。也有一些学生问过我这样的题,我给学生讲之前,都说,不建议做这个题,外心2019年有可以不考了,可能考内心,即使考外心的话,也不会这么大难度,把前几年的题会了就行了。中考试题一公布,发现考了一个极简单而基础的尺规作图作出三角形的外心的题。这是符合中考出题的心理的,中考对于平时教学的导向性而强,对于一个考点考的过多,过难,会对下一年老师们的教学备考产生很大影响。
201923(源自课本人教版八上)
如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心。
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC解:(1)在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
∴∠BAC=∠DAE
又∵∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC.
∴∠BAD=∠CAE.
(2)
∵AD=6,AP=x,
∴PD=6-x.
当AD⊥BC时,AP=最小,即为PD的最大值。
(3)如图,设,则,
∵AB⊥AC,
∴
∵I为△APC的内心,
∴AI、CI分别平分∠PAC、∠PCA,
∴,
∵,,即,
∴m=105,n=150.
2016年的第9题就是由2010年的第6题改编而来。
2018年的第15题和2019年的第23题都考的内心,都源自课本。
外心:三角形外接圆的圆心(三角形三边的垂直平分线的交点)。圆和三角形的位置关系是圆在三角形的外部,所以叫外接圆的圆心,简称外心。
外心的特点:锐角三角形的外心在三角形的内部,直角三角形的外心在斜边中点,钝角三角形的外心在三角形外部,并且在最大的角所对的方向。
现在分析河北省近几年外心考点。
2010年是河北省第一考外心,虽然没有出现外心这个词,但是连接A、B、C三点,形成△ABC,
△ABC是钝角三角形,找三角形的外心,找任意两个边的垂直平分线的交点即可。首先画出AB边的垂直平分线,可以确实外心为Q点或M点,再画出BC的垂直平分线,交点为Q.
20106.如图3,在5×5正方形网格中,一条圆弧经过A,B,C三点,
那么这条圆弧所在圆的圆心是(
)A.点P
B.点Q
C.点R
D.点M
分析:这是河北省刚开始考尺规作图时设计的此题,考到了线段垂直平分线的画法,钝角三角形的外心。
20156.如图3,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是(
)
A.△ABE
B.△ACF
C.△ABD
D.△ADE
此题设计出了锐角、直角、钝角三角形的外心的位置考点,同学们要总结一下。
20169.图示为4×4的网格图,A,B,C,D,O均在格点上,点O是(
)
A.△ACD的外心
B.△ABC的外心
C.△ACD的内心
D.△ABC的内心
此题考到了钝角三角形的外心在三角形的外部。
选项A,
△ACD是直角三角形,外心在斜边的中点;
选项B,△ABC是钝角三角形,外心在三角形的外部,在任意两边的垂直平分线上,作出AC的垂直平分线,和BC的垂直平分线可,如下图
选项C.△ACD的内心我们也要在图中用尺规画出来,既然出现了内心,就显示出明年可以考内心这个考点。
选项D.△ABC的内心也要在图中用尺规画出来。
注意:内心是三角形三条角一部分线的交点,三角形内切圆的圆心。如下图
同学们做完此题后,把这个题和2010年的做个对比。
201723.如图,,为中点,点在线段上(不与点,重合),将绕点逆时针旋转后得到扇形,,分别切优弧于点,,且点,在异侧,连接.
(1)求证:;
(2)当时,求的长(结果保留);
(3)若的外心在扇形的内部,求的取值范围.
分析:(1)求证:;
观察和△,可用全等,三角函数和勾股定理解决,同学们可以思考一
下这几个方法。
(2)当时,求的长(结果保留);
考点:三角函数,OB=8,
,∠Q是直角,
∴
∴OQ=4∴∠B=30°
∠BOQ=60°
∴所对的圆心角为210°
∴
(3)若的外心在扇形的内部,求的取值范围.
锐角三角形的外心在三角形的内部。
思考:当OC=8时,点P与点A重合,不存在。此处应用心思考,2019年考内心时就涉及到了两点重合时产情况。所以,动点问题,我们一定要化动为静,先找到起点、终点、及中间的特殊点。思考时,不要漏。
201823
如图13,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意一点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM?△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
解:(1)
∵点P为AB的中点,∴
AP=BP.
在△APM和△BPN中,
∴△APM和△BPN(ASA)
(2)由(1),得△APM和△BPN,∴PM=PN.∴2PN=MN.
又∵MN=2BN,
∴PN=BN.
∴.
(3)
.
【提示:外心所在的位置与三角形的形状有关,锐角三角形的外心在三角形内部,直角三角形的外心在斜边中点处,钝角三角形的外心在三角形的外部。只需求出△BPN为锐角三角形时,的取值范围。】
201815内心
内心是三角形三条角一部分线的交点,三角形内切圆的圆心。如下图
下面这个题源自课本(人教版八上)
如图点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使共顶点与I重合,则图中阴影部分的周长为(
)
A.4.5
B.4
C.3
D.2
三角形的内心是任意两条角平分线的交点,平移产生平行。
角平分线+平行,产生等腰三角形。
2019年第10题,用尺规作图作出三角形的外心,符合物极必反的规律。三角形的外心连续考了好几年了,锐角三角形、钝角三角形、直角三角形都考过了。很多朋友设计了好多高难度的外心的题,进行中考前模拟训练。也有一些学生问过我这样的题,我给学生讲之前,都说,不建议做这个题,外心2019年有可以不考了,可能考内心,即使考外心的话,也不会这么大难度,把前几年的题会了就行了。中考试题一公布,发现考了一个极简单而基础的尺规作图作出三角形的外心的题。这是符合中考出题的心理的,中考对于平时教学的导向性而强,对于一个考点考的过多,过难,会对下一年老师们的教学备考产生很大影响。
201923(源自课本人教版八上)
如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心。
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC
∴△ABC≌△ADE(SAS).
∴∠BAC=∠DAE
又∵∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC.
∴∠BAD=∠CAE.
(2)
∵AD=6,AP=x,
∴PD=6-x.
当AD⊥BC时,AP=最小,即为PD的最大值。
(3)如图,设,则,
∵AB⊥AC,
∴
∵I为△APC的内心,
∴AI、CI分别平分∠PAC、∠PCA,
∴,
∵,,即,
∴m=105,n=150.
同课章节目录
