湘教版八上数学2.5.2全等三角形的判定(SAS)课件(21张ppt)
文档属性
| 名称 | 湘教版八上数学2.5.2全等三角形的判定(SAS)课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 16:43:48 | ||
图片预览




文档简介
(共21张PPT)
一、创设情境,导入新课
1、什么叫全等图形?
能够完全重合的两个图形叫作全等图形;
2、全等三角形有哪些性质?
三组对应边相等;
三组对应角相等。
什么叫全等三角形?
能够完全重合的两个三角形叫作全等三角形。
3、两个三角形满足什么条件就能全等呢?
二、合作交流,新知探究
要画一个三角形与原三角形全等,至少需要几个与边或角大小有关的条件呢?
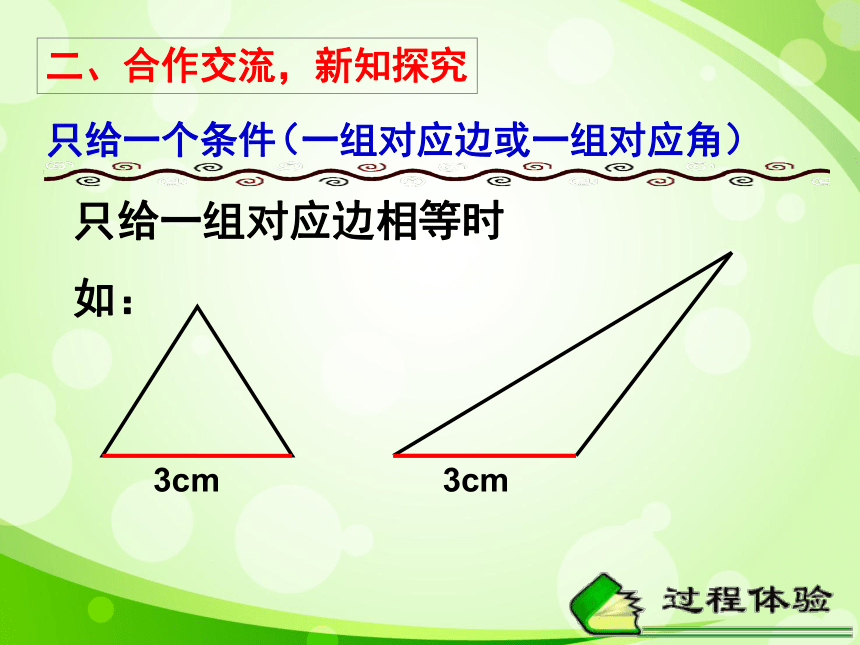
3cm
3cm
二、合作交流,新知探究
只给一个条件
(一组对应边或一组对应角)
只给一组对应边相等时
如:
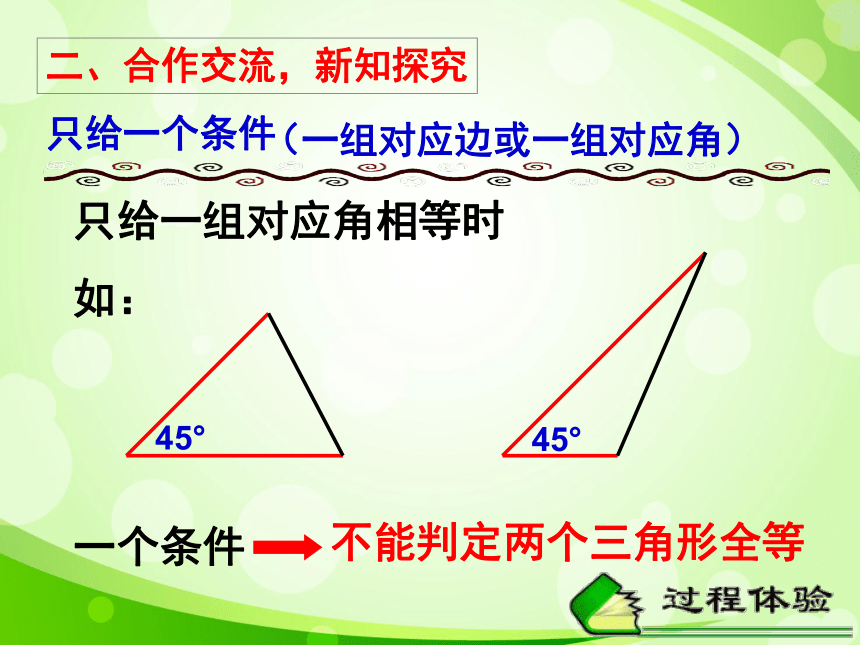
只给一组对应角相等时
如:
45°
45°
只给一个条件
一个条件
不能判定两个三角形全等
二、合作交流,新知探究
(一组对应边或一组对应角)
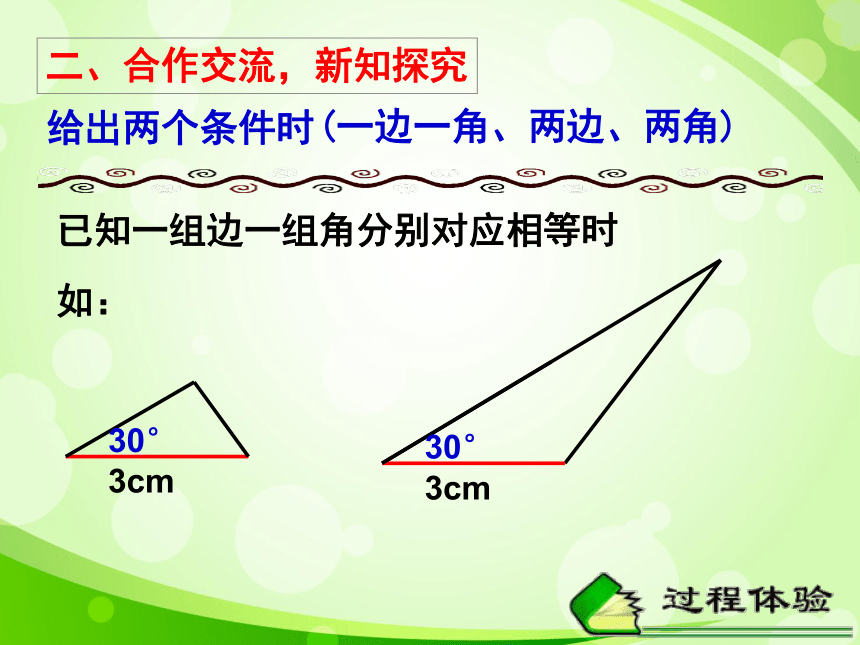
已知一组边一组角分别对应相等时
如:
3cm
3cm
30°
30°
给出两个条件时
二、合作交流,新知探究
(一边一角、两边、两角)
给出两个条件时(一边一角、两边、两角)
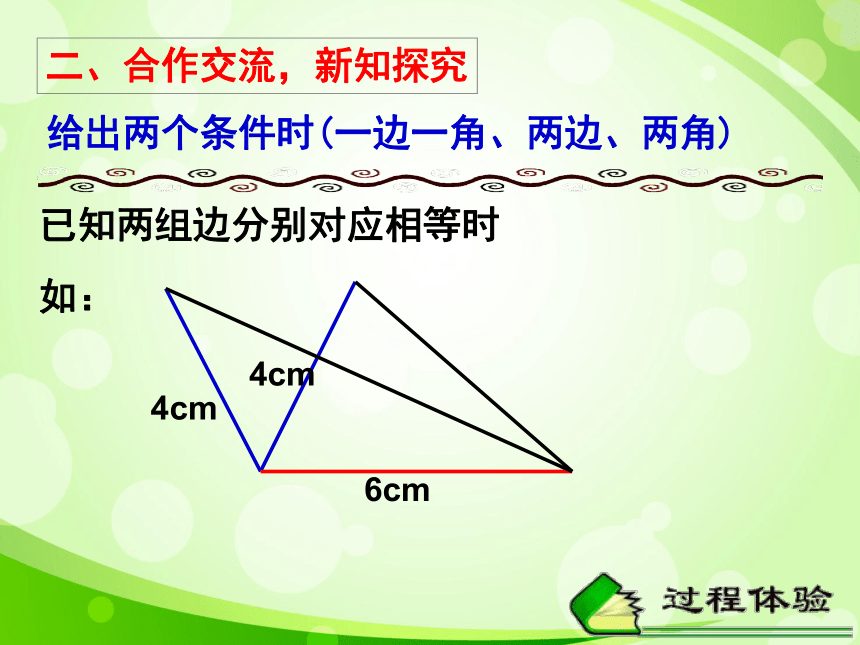
已知两组边分别对应相等时
如:
6cm
4cm
4cm
二、合作交流,新知探究
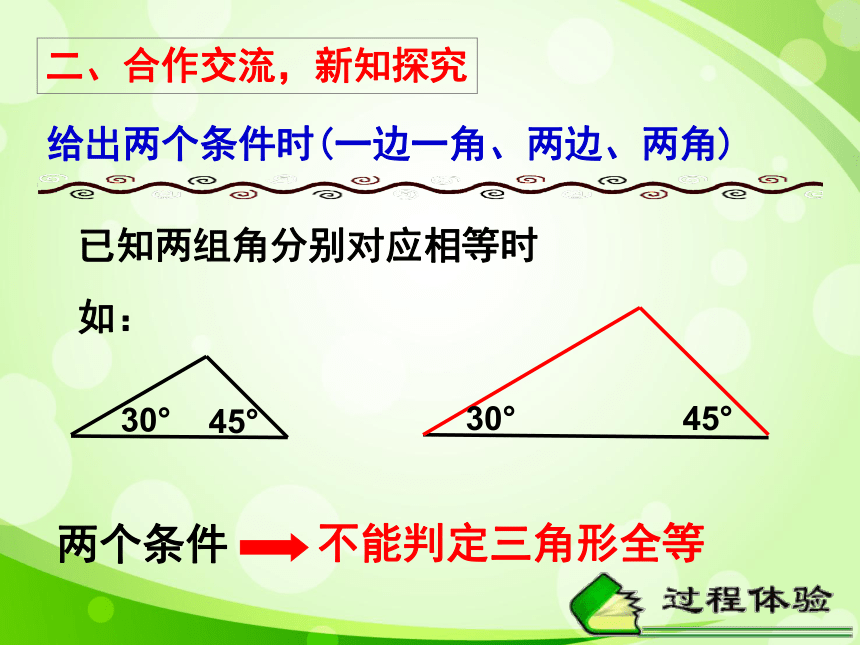
给出两个条件时(一边一角、两边、两角)
已知两组角分别对应相等时
如:
30°
45°
30°
45°
二、合作交流,新知探究
两个条件
不能判定三角形全等
那给出三个条件呢?它有哪些可能?
二、合作交流,新知探究
两边一角分别对应相等
两角一边分别对应相等
三边分别对应相等
三角分别对应相等
【分组合作】
1、画有一个角为30°的三角形,并使这角
的两边分别为2cm、3cm,并裁下来;
2、画有一个角为45°的三角形,并使这角
的两边分别为3cm、4cm,并裁下来;
3、画有一个角为60°的三角形,并使这角
的两边分别为4cm、5cm,并裁下来.
【合作交流】请把你裁下来的三角形与同桌的进
行比较,你有什么发现?
重合
二、合作交流,新知探究
猜测:
二、合作交流,新知探究
有两边和它们的夹角分别相等的两个三角形全等。
验证:
1.平移
60°
A'
B'
C'
2
3
60°
A
B
C
2
3
通过平移发现:这两个三角形全等!
猜测:
二、合作交流,新知探究
有两边和它们的夹角分别相等的两个三角形全等。
验证:
2.旋转
A
B
A'
B'
O
.
A'
B'
45°
45°
3
3
4
4
通过旋转发现:这两个三角形全等!
猜测:
二、合作交流,新知探究
有两边和它们的夹角分别相等的两个三角形全等。
验证:
3.翻折(轴反射)
通过翻折发现:这两个三角形全等!
4
4
5
5
60°
60°
A
A'
B
C
C'
B'
二、合作交流,新知探究
结论:
两边及其夹角分别相等的两个三角形全等.
简记为边角边
几何语言:
在△ABC与△A'B'C'中
A
B
C
A'
B'
C'
∴△ABC≌△A'B'C'
∵
AB=A'B'
∠B=∠B'
BC=B'C'
全等三角形的判定定理:
(或SAS).
(SAS)
三、应用迁移,知识巩固
例1.如图,AB和CD相交于点O,且AO=BO,
CO=DO.求证:△ACO
≌
△BDO.
A
C
B
D
O
四、思维拓展,能力提升
例2.已知:如图,AB=AC,点E、F分别是AC,
AB的中点.求证:BE=CF.
B
E
F
A
C
F
A
C
A
E
B
A
E
B
F
A
C
A
B
D
A
B
C
SSA不能
判定全等
四、思维迁移,拓展延伸
思考:
两边及其这两边任意一边的对角分别相等,能判断两个三角形全等吗?
即SSA能判断两个三角形全等吗?
五、学习小结
1、识别两个三角形全等的方法是什么?
2、在运用SAS定理证明两个三角形全等时,
需要注意什么?
六、当堂检测
1.如图(1),AB=AC,要使△ABD
≌
△ACD,
应添加的条件是
.
(应用"SAS"定理,请添加一个条件)
2.如图(2),AD∥BC,AD=BC.问△ADC和△CBA
是全等三角形吗?为什么?
C
B
A
D
图(1)
A
B
C
D
图(2)
必做题:
选做题:
如图,E、F是四边形ABCD的对角线BD上的两点,
AE
CF,BE=DF.
求证:△ADE
≌
△CBF
A
B
C
D
E
F
六、当堂检测
一、创设情境,导入新课
1、什么叫全等图形?
能够完全重合的两个图形叫作全等图形;
2、全等三角形有哪些性质?
三组对应边相等;
三组对应角相等。
什么叫全等三角形?
能够完全重合的两个三角形叫作全等三角形。
3、两个三角形满足什么条件就能全等呢?
二、合作交流,新知探究
要画一个三角形与原三角形全等,至少需要几个与边或角大小有关的条件呢?
3cm
3cm
二、合作交流,新知探究
只给一个条件
(一组对应边或一组对应角)
只给一组对应边相等时
如:
只给一组对应角相等时
如:
45°
45°
只给一个条件
一个条件
不能判定两个三角形全等
二、合作交流,新知探究
(一组对应边或一组对应角)
已知一组边一组角分别对应相等时
如:
3cm
3cm
30°
30°
给出两个条件时
二、合作交流,新知探究
(一边一角、两边、两角)
给出两个条件时(一边一角、两边、两角)
已知两组边分别对应相等时
如:
6cm
4cm
4cm
二、合作交流,新知探究
给出两个条件时(一边一角、两边、两角)
已知两组角分别对应相等时
如:
30°
45°
30°
45°
二、合作交流,新知探究
两个条件
不能判定三角形全等
那给出三个条件呢?它有哪些可能?
二、合作交流,新知探究
两边一角分别对应相等
两角一边分别对应相等
三边分别对应相等
三角分别对应相等
【分组合作】
1、画有一个角为30°的三角形,并使这角
的两边分别为2cm、3cm,并裁下来;
2、画有一个角为45°的三角形,并使这角
的两边分别为3cm、4cm,并裁下来;
3、画有一个角为60°的三角形,并使这角
的两边分别为4cm、5cm,并裁下来.
【合作交流】请把你裁下来的三角形与同桌的进
行比较,你有什么发现?
重合
二、合作交流,新知探究
猜测:
二、合作交流,新知探究
有两边和它们的夹角分别相等的两个三角形全等。
验证:
1.平移
60°
A'
B'
C'
2
3
60°
A
B
C
2
3
通过平移发现:这两个三角形全等!
猜测:
二、合作交流,新知探究
有两边和它们的夹角分别相等的两个三角形全等。
验证:
2.旋转
A
B
A'
B'
O
.
A'
B'
45°
45°
3
3
4
4
通过旋转发现:这两个三角形全等!
猜测:
二、合作交流,新知探究
有两边和它们的夹角分别相等的两个三角形全等。
验证:
3.翻折(轴反射)
通过翻折发现:这两个三角形全等!
4
4
5
5
60°
60°
A
A'
B
C
C'
B'
二、合作交流,新知探究
结论:
两边及其夹角分别相等的两个三角形全等.
简记为边角边
几何语言:
在△ABC与△A'B'C'中
A
B
C
A'
B'
C'
∴△ABC≌△A'B'C'
∵
AB=A'B'
∠B=∠B'
BC=B'C'
全等三角形的判定定理:
(或SAS).
(SAS)
三、应用迁移,知识巩固
例1.如图,AB和CD相交于点O,且AO=BO,
CO=DO.求证:△ACO
≌
△BDO.
A
C
B
D
O
四、思维拓展,能力提升
例2.已知:如图,AB=AC,点E、F分别是AC,
AB的中点.求证:BE=CF.
B
E
F
A
C
F
A
C
A
E
B
A
E
B
F
A
C
A
B
D
A
B
C
SSA不能
判定全等
四、思维迁移,拓展延伸
思考:
两边及其这两边任意一边的对角分别相等,能判断两个三角形全等吗?
即SSA能判断两个三角形全等吗?
五、学习小结
1、识别两个三角形全等的方法是什么?
2、在运用SAS定理证明两个三角形全等时,
需要注意什么?
六、当堂检测
1.如图(1),AB=AC,要使△ABD
≌
△ACD,
应添加的条件是
.
(应用"SAS"定理,请添加一个条件)
2.如图(2),AD∥BC,AD=BC.问△ADC和△CBA
是全等三角形吗?为什么?
C
B
A
D
图(1)
A
B
C
D
图(2)
必做题:
选做题:
如图,E、F是四边形ABCD的对角线BD上的两点,
AE
CF,BE=DF.
求证:△ADE
≌
△CBF
A
B
C
D
E
F
六、当堂检测
同课章节目录
