沪科版九年级下册24.4直线与圆的位置关系强化训练(Word版 无答案)
文档属性
| 名称 | 沪科版九年级下册24.4直线与圆的位置关系强化训练(Word版 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 825.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 00:00:00 | ||
图片预览

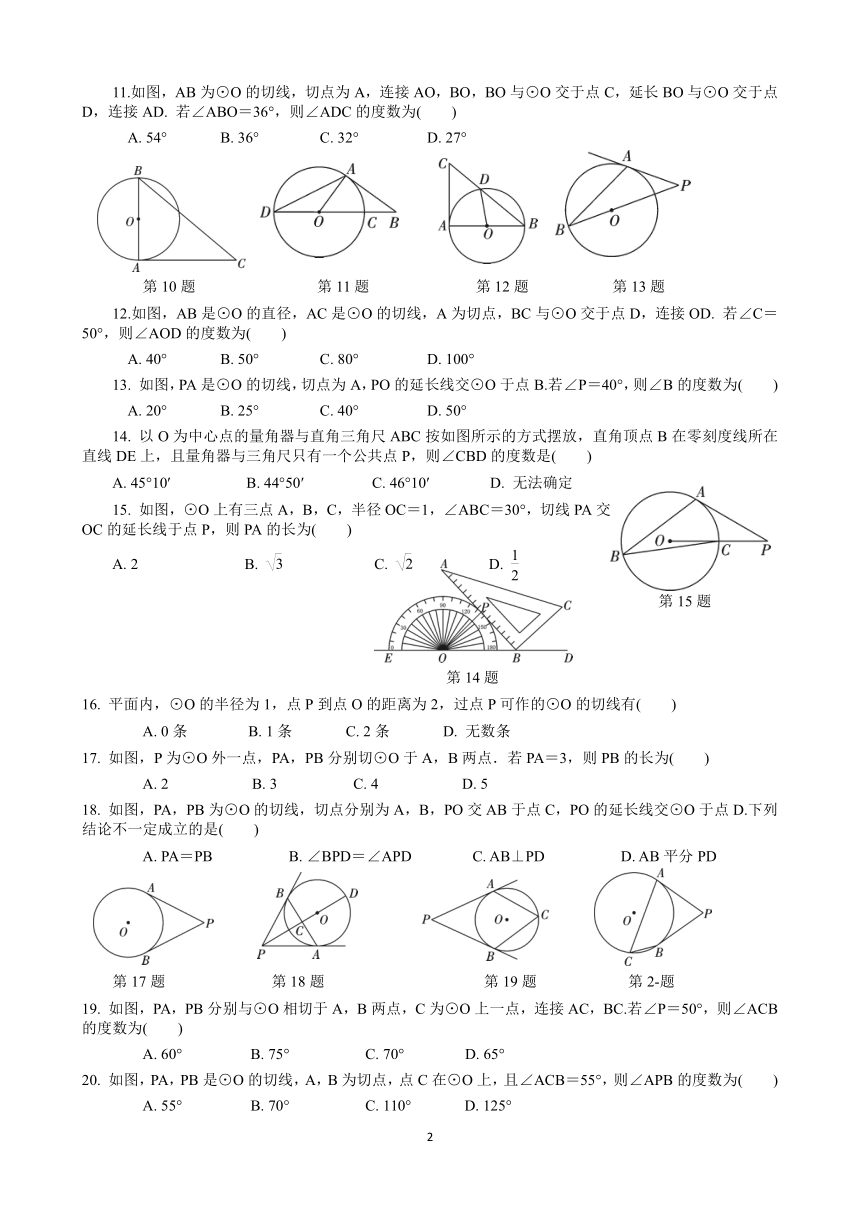

文档简介
直线与圆的位置关系
一、选择题
1.半径为3的⊙P的圆心坐标为(2,4),则⊙P与x轴的位置关系是( )
A.相交
B.相离
C.相切
D.以上都不是
2.如图,点A,B,C在⊙O上,过点A作⊙O的切线交OC的延长线于点P,∠B=30°,OP=3,则AP的长为( )
A.3
B.
C.
D.
如图所示,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( ))
A.2.3
B.2.4
C.2.5
D.2.6
第2题
第3题
第4题
第5题
如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,则下列结论中,不正确的是( )
A.∠F=∠AOC
B.AB⊥BF
C.CE是⊙O的切线
D.=
6.
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线BA绕点B按顺时针方向旋转( )
A.40°或80°
B.50°或110°
C.50°或100°
D.60°或120°
第6题
第7题
第8题
第9题
7.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与AC,BC分别相交于点P,Q,则线段PQ长的最小值为( )
A.5
B.
4
C.4.75
D.4.8
8.如图,PA,PB分别切⊙O于A,B两点,∠P=40°,则∠C的度数为( )
A.40°
B.140°
C.70°
D.80°
9.如图,PA,PB分别与⊙O相切于A,B两点,点E在上,过点E作⊙O的切线,分别与PA,PB相交于点C,D.若PA=3
cm,则△PCD的周长等于( )
A.3
cm
B.6
cm
C.9
cm
D.12
cm
10.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点.若∠C=40°,则∠B的度数为( )
A.
60°
B.
50°
C.
40°
D.
30°
11.如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.
若∠ABO=36°,则∠ADC的度数为( )
A.
54°
B.
36°
C.
32°
D.
27°
第10题
第11题
第12题
第13题
12.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.
若∠C=50°,则∠AOD的度数为( )
A.
40°
B.
50°
C.
80°
D.
100°
13.
如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B.若∠P=40°,则∠B的度数为( )
A.
20°
B.
25°
C.
40°
D.
50°
14.
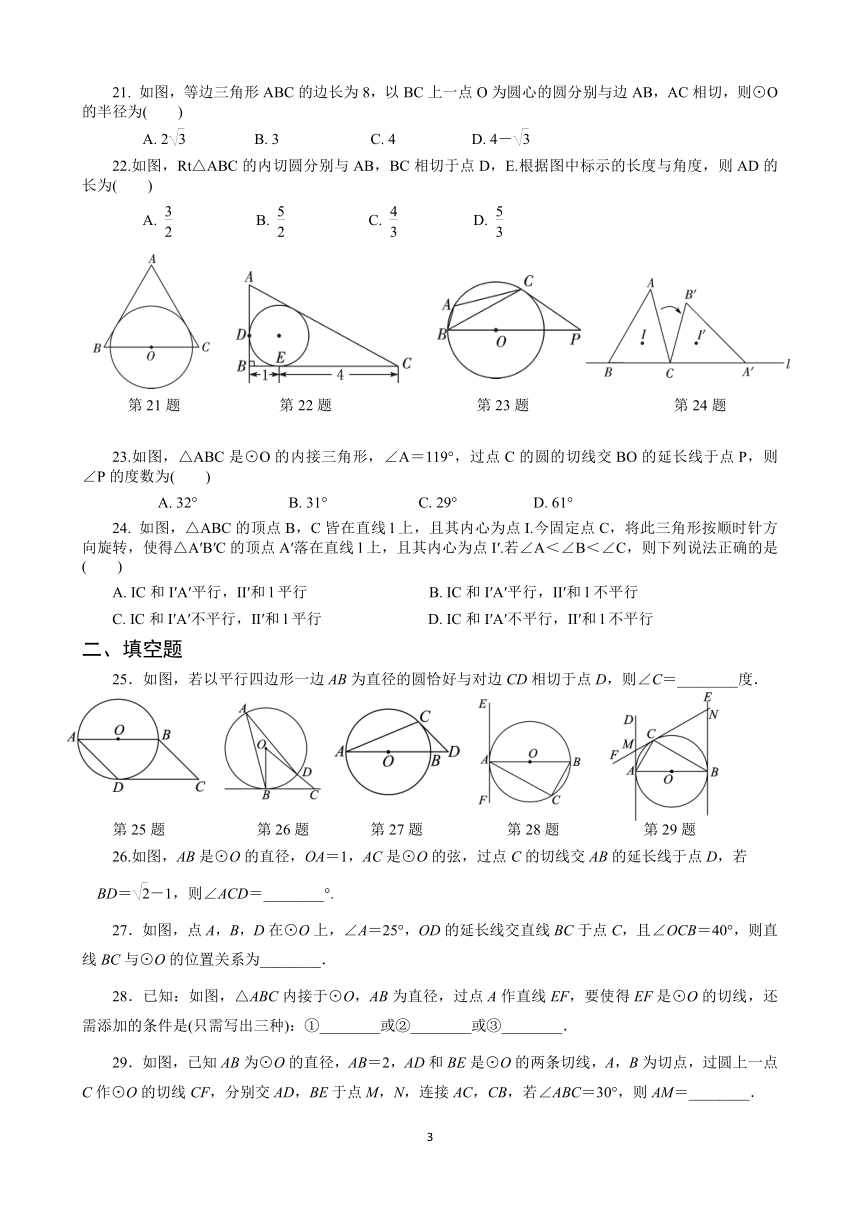
以O为中心点的量角器与直角三角尺ABC按如图所示的方式摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角尺只有一个公共点P,则∠CBD的度数是( )
A.
45°10′
B.
44°50′
C.
46°10′
D.
无法确定
15.
如图,⊙O上有三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.
2
B.
C.
D.
第15题
第14题
16.
平面内,⊙O的半径为1,点P到点O的距离为2,过点P可作的⊙O的切线有( )
A.
0条
B.
1条
C.
2条
D.
无数条
17.
如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB的长为( )
A.
2
B.
3
C.
4
D.
5
18.
如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D.下列结论不一定成立的是( )
A.
PA=PB
B.
∠BPD=∠APD
C.
AB⊥PD
D.
AB平分PD
第17题
第18题
第19题
第2-题
19.
如图,PA,PB分别与⊙O相切于A,B两点,C为⊙O上一点,连接AC,BC.若∠P=50°,则∠ACB的度数为( )
A.
60°
B.
75°
C.
70°
D.
65°
20.
如图,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,且∠ACB=55°,则∠APB的度数为( )
A.
55°
B.
70°
C.
110°
D.
125°
21.
如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.
2
B.
3
C.
4
D.
4-
22.如图,Rt△ABC的内切圆分别与AB,BC相切于点D,E.根据图中标示的长度与角度,则AD的长为( )
A.
B.
C.
D.
第21题
第22题
第23题
第24题
23.如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO的延长线于点P,则∠P的度数为( )
A.
32°
B.
31°
C.
29°
D.
61°
24.
如图,△ABC的顶点B,C皆在直线l上,且其内心为点I.今固定点C,将此三角形按顺时针方向旋转,使得△A′B′C的顶点A′落在直线l上,且其内心为点I′.若∠A<∠B<∠C,则下列说法正确的是( )
A.
IC和I′A′平行,II′和l平行
B.
IC和I′A′平行,II′和l不平行
C.
IC和I′A′不平行,II′和l平行
D.
IC和I′A′不平行,II′和l不平行
二、填空题
25.如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=________度.
第25题
第26题
第27题
第28题
第29题
26.如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若
BD=-1,则∠ACD=________°.
27.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,则直线BC与⊙O的位置关系为________.
28.已知:如图,△ABC内接于⊙O,AB为直径,过点A作直线EF,要使得EF是⊙O的切线,还需添加的条件是(只需写出三种):①________或②________或③________.
29.如图,已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A,B为切点,过圆上一点C作⊙O的切线CF,分别交AD,BE于点M,N,连接AC,CB,若∠ABC=30°,则AM=________.
30.
如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=________.
31.
如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上.若∠P=102°,则∠A+∠C=________.
第30题
第31题
第33题
第34题
32.
直角三角形的两条直角边分别是5和12,则它的内切圆半径为________.
33.
如图,AB为⊙O的直径,C为⊙O上一点,过点B的切线交AC的延长线于点D,E为弦AC的中点,
AD=10,BD=6.若P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为__________.
34.如图,直线y=-x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,1个单位
度为半径作⊙P.当⊙P与直线AB相切时,点P的坐标是__________________.
解答题
35.如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
36.如图,已知A,B,C,D,E是⊙O上的五点,⊙O的直径BE=2
,∠BCD=120°,A为的中点,延长BA到点P,使BA=AP,连接PE.
(1)求线段BD的长;
(2)求证:直线PE是⊙O的切线.
37.如图,已知正方形ABCD的边长为2,M是BC的中点,P是线段MC上的一个动点,点P不与点M和点C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.
求四边形CDFP的周长.
38.综合探究如图K-9-15,AB是⊙O的直径,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.
(1)探究线段PB,AB之间的数量关系,并说明理由;
(2)若AD=3,求AB的长.
39..
如图,AB是⊙O的直径,P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)
求证:OP∥BC.
(2)
过点C作⊙O的切线CD,交AP的延长线于点D.
如果∠D=90°,DP=1,求⊙O的直径.
40.如图,在△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O分别交AC,BC于点D,E,过点E作⊙O的切线EF交AC于点F,连接BD.
(1)
求证:EF是△CDB的中位线;
(2)
求EF的长.
41.如图,五边形ABCDE内接于⊙O,CF与⊙O相切于点C,交AB的延长线于点F.
(1)
若AE=DC,∠E=∠BCD,求证:DE=BC;
(2)
若OB=2,AB=BD=DA,∠F=45°,求CF的长.
42.
如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)
求证:DG∥CA;
(2)
求证:AD=ID;
(3)
若DE=4,BE=5,求BI的长.
43.
如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)
求证:∠A=∠DOB.
(2)
DE与⊙O有怎样的位置关系?请说明理由.
44.
如图①,AB为半圆O的直径,AF为半圆O的切线,过半圆O上的点C作CD∥AB交AF于点D,连接BC.
(1)
连接DO,若BC∥OD,求证:CD是半圆O的切线;
(2)
如图②,当线段CD与半圆O交于点E时,连接AE,AC,判断∠AED和∠ACD之间的数量关系,并证明你的结论.
45.
如图,AB是⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.
(1)
试判断直线DE与⊙O的位置关系,并说明理由;
(2)
若⊙O的半径为2,∠BAC=60°,求线段EF的长.
46.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)
求证:MF是⊙O的切线;
(2)
若CN=3,BN=4,求CM的长.
47.如图,AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于点E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长,交BA的延长线于点F.
(1)
求证:DC是⊙O的切线;
(2)
若∠ABC=30°,AB=8,求线段CF的长.
48.
如图,BD是⊙O的直径,弦BC与OA相交于点E,AF与⊙O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.
求:
(1)
∠ADB的度数;
(2)
AC的长.
49.
如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点A的切线与CD的延长线相交于点P,且∠APC=∠BCP.
(1)
求证:∠BAC=2∠ACD.
(2)
过点D作DE⊥AC,垂足为E.当BC=6,AE=2时,求⊙O的半径.
12
一、选择题
1.半径为3的⊙P的圆心坐标为(2,4),则⊙P与x轴的位置关系是( )
A.相交
B.相离
C.相切
D.以上都不是
2.如图,点A,B,C在⊙O上,过点A作⊙O的切线交OC的延长线于点P,∠B=30°,OP=3,则AP的长为( )
A.3
B.
C.
D.
如图所示,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( ))
A.2.3
B.2.4
C.2.5
D.2.6
第2题
第3题
第4题
第5题
如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,则下列结论中,不正确的是( )
A.∠F=∠AOC
B.AB⊥BF
C.CE是⊙O的切线
D.=
6.
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线BA绕点B按顺时针方向旋转( )
A.40°或80°
B.50°或110°
C.50°或100°
D.60°或120°
第6题
第7题
第8题
第9题
7.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与AC,BC分别相交于点P,Q,则线段PQ长的最小值为( )
A.5
B.
4
C.4.75
D.4.8
8.如图,PA,PB分别切⊙O于A,B两点,∠P=40°,则∠C的度数为( )
A.40°
B.140°
C.70°
D.80°
9.如图,PA,PB分别与⊙O相切于A,B两点,点E在上,过点E作⊙O的切线,分别与PA,PB相交于点C,D.若PA=3
cm,则△PCD的周长等于( )
A.3
cm
B.6
cm
C.9
cm
D.12
cm
10.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点.若∠C=40°,则∠B的度数为( )
A.
60°
B.
50°
C.
40°
D.
30°
11.如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.
若∠ABO=36°,则∠ADC的度数为( )
A.
54°
B.
36°
C.
32°
D.
27°
第10题
第11题
第12题
第13题
12.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.
若∠C=50°,则∠AOD的度数为( )
A.
40°
B.
50°
C.
80°
D.
100°
13.
如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B.若∠P=40°,则∠B的度数为( )
A.
20°
B.
25°
C.
40°
D.
50°
14.
以O为中心点的量角器与直角三角尺ABC按如图所示的方式摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角尺只有一个公共点P,则∠CBD的度数是( )
A.
45°10′
B.
44°50′
C.
46°10′
D.
无法确定
15.
如图,⊙O上有三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.
2
B.
C.
D.
第15题
第14题
16.
平面内,⊙O的半径为1,点P到点O的距离为2,过点P可作的⊙O的切线有( )
A.
0条
B.
1条
C.
2条
D.
无数条
17.
如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB的长为( )
A.
2
B.
3
C.
4
D.
5
18.
如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D.下列结论不一定成立的是( )
A.
PA=PB
B.
∠BPD=∠APD
C.
AB⊥PD
D.
AB平分PD
第17题
第18题
第19题
第2-题
19.
如图,PA,PB分别与⊙O相切于A,B两点,C为⊙O上一点,连接AC,BC.若∠P=50°,则∠ACB的度数为( )
A.
60°
B.
75°
C.
70°
D.
65°
20.
如图,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,且∠ACB=55°,则∠APB的度数为( )
A.
55°
B.
70°
C.
110°
D.
125°
21.
如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.
2
B.
3
C.
4
D.
4-
22.如图,Rt△ABC的内切圆分别与AB,BC相切于点D,E.根据图中标示的长度与角度,则AD的长为( )
A.
B.
C.
D.
第21题
第22题
第23题
第24题
23.如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO的延长线于点P,则∠P的度数为( )
A.
32°
B.
31°
C.
29°
D.
61°
24.
如图,△ABC的顶点B,C皆在直线l上,且其内心为点I.今固定点C,将此三角形按顺时针方向旋转,使得△A′B′C的顶点A′落在直线l上,且其内心为点I′.若∠A<∠B<∠C,则下列说法正确的是( )
A.
IC和I′A′平行,II′和l平行
B.
IC和I′A′平行,II′和l不平行
C.
IC和I′A′不平行,II′和l平行
D.
IC和I′A′不平行,II′和l不平行
二、填空题
25.如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=________度.
第25题
第26题
第27题
第28题
第29题
26.如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若
BD=-1,则∠ACD=________°.
27.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,则直线BC与⊙O的位置关系为________.
28.已知:如图,△ABC内接于⊙O,AB为直径,过点A作直线EF,要使得EF是⊙O的切线,还需添加的条件是(只需写出三种):①________或②________或③________.
29.如图,已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A,B为切点,过圆上一点C作⊙O的切线CF,分别交AD,BE于点M,N,连接AC,CB,若∠ABC=30°,则AM=________.
30.
如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=________.
31.
如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上.若∠P=102°,则∠A+∠C=________.
第30题
第31题
第33题
第34题
32.
直角三角形的两条直角边分别是5和12,则它的内切圆半径为________.
33.
如图,AB为⊙O的直径,C为⊙O上一点,过点B的切线交AC的延长线于点D,E为弦AC的中点,
AD=10,BD=6.若P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为__________.
34.如图,直线y=-x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,1个单位
度为半径作⊙P.当⊙P与直线AB相切时,点P的坐标是__________________.
解答题
35.如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
36.如图,已知A,B,C,D,E是⊙O上的五点,⊙O的直径BE=2
,∠BCD=120°,A为的中点,延长BA到点P,使BA=AP,连接PE.
(1)求线段BD的长;
(2)求证:直线PE是⊙O的切线.
37.如图,已知正方形ABCD的边长为2,M是BC的中点,P是线段MC上的一个动点,点P不与点M和点C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.
求四边形CDFP的周长.
38.综合探究如图K-9-15,AB是⊙O的直径,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.
(1)探究线段PB,AB之间的数量关系,并说明理由;
(2)若AD=3,求AB的长.
39..
如图,AB是⊙O的直径,P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)
求证:OP∥BC.
(2)
过点C作⊙O的切线CD,交AP的延长线于点D.
如果∠D=90°,DP=1,求⊙O的直径.
40.如图,在△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O分别交AC,BC于点D,E,过点E作⊙O的切线EF交AC于点F,连接BD.
(1)
求证:EF是△CDB的中位线;
(2)
求EF的长.
41.如图,五边形ABCDE内接于⊙O,CF与⊙O相切于点C,交AB的延长线于点F.
(1)
若AE=DC,∠E=∠BCD,求证:DE=BC;
(2)
若OB=2,AB=BD=DA,∠F=45°,求CF的长.
42.
如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)
求证:DG∥CA;
(2)
求证:AD=ID;
(3)
若DE=4,BE=5,求BI的长.
43.
如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)
求证:∠A=∠DOB.
(2)
DE与⊙O有怎样的位置关系?请说明理由.
44.
如图①,AB为半圆O的直径,AF为半圆O的切线,过半圆O上的点C作CD∥AB交AF于点D,连接BC.
(1)
连接DO,若BC∥OD,求证:CD是半圆O的切线;
(2)
如图②,当线段CD与半圆O交于点E时,连接AE,AC,判断∠AED和∠ACD之间的数量关系,并证明你的结论.
45.
如图,AB是⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.
(1)
试判断直线DE与⊙O的位置关系,并说明理由;
(2)
若⊙O的半径为2,∠BAC=60°,求线段EF的长.
46.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)
求证:MF是⊙O的切线;
(2)
若CN=3,BN=4,求CM的长.
47.如图,AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于点E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长,交BA的延长线于点F.
(1)
求证:DC是⊙O的切线;
(2)
若∠ABC=30°,AB=8,求线段CF的长.
48.
如图,BD是⊙O的直径,弦BC与OA相交于点E,AF与⊙O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.
求:
(1)
∠ADB的度数;
(2)
AC的长.
49.
如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点A的切线与CD的延长线相交于点P,且∠APC=∠BCP.
(1)
求证:∠BAC=2∠ACD.
(2)
过点D作DE⊥AC,垂足为E.当BC=6,AE=2时,求⊙O的半径.
12
