18.2.3正方形(2) 课件(共24张PPT)
文档属性
| 名称 | 18.2.3正方形(2) 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:00:44 | ||
图片预览



文档简介
(共24张PPT)
人教版
八年级数学上
18.2.3正方形(2)
学习目标
1.探索并证明正方形的判定,并了解平行四边形、矩形、菱形之间的
联系和区别;(重点、难点)
2.会运用正方形的判定条件进行有关的论证和计算
.(难点)
回顾旧知
思考1:
正方形有哪些性质?
A
B
C
D
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
O
合作探究---正方形的判定
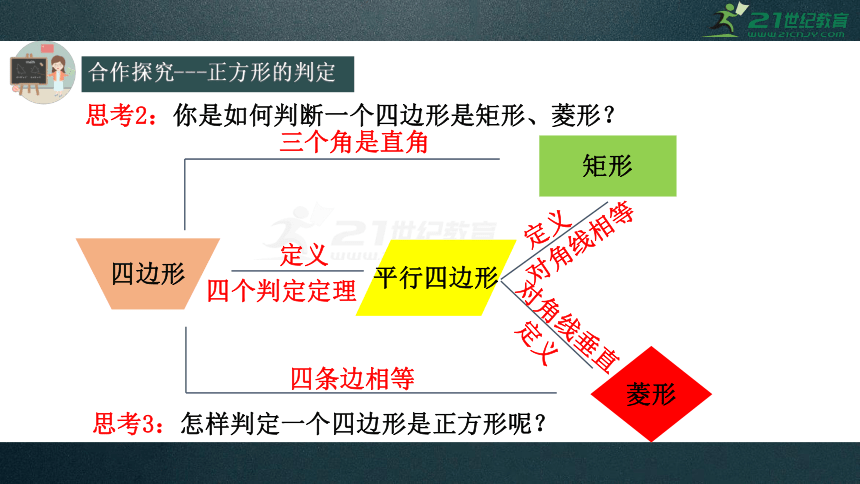
思考2:你是如何判断一个四边形是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
思考3:怎样判定一个四边形是正方形呢?
合作探究---正方形的判定
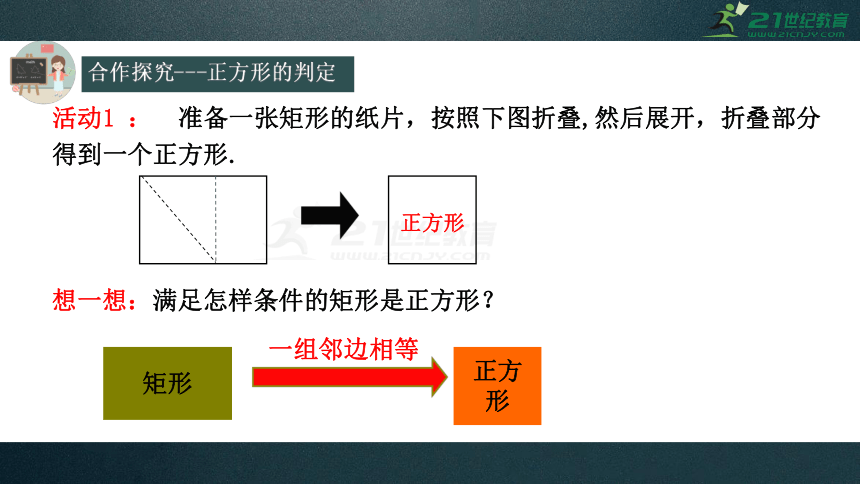
活动1
:
准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形.
正方形
想一想:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
合作探究---正方形的判定
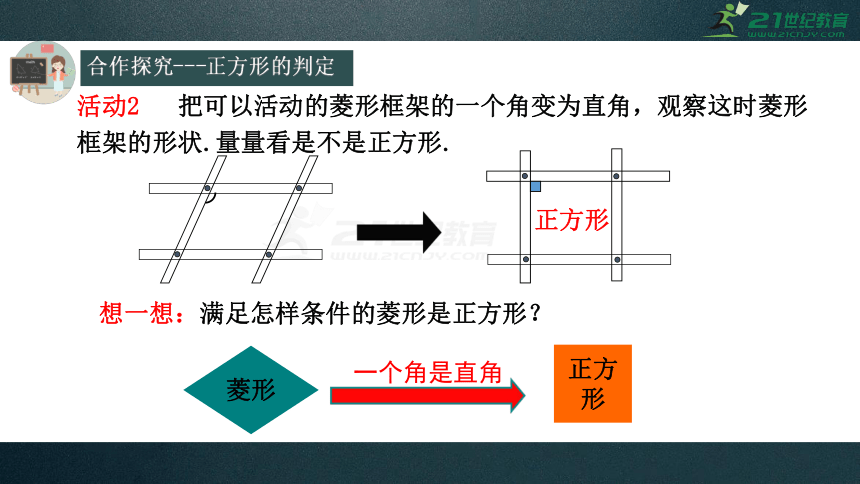
活动2
把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
想一想:满足怎样条件的菱形是正方形?
正方形
一个角是直角
合作探究---正方形的判定
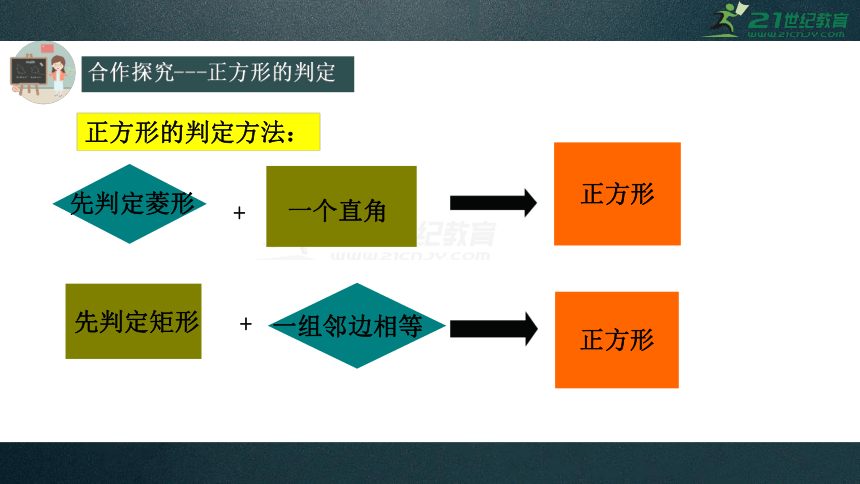
正方形的判定方法:
正方形
正方形
+
+
先判定菱形
先判定矩形
一个直角
一组邻边相等
典例精析
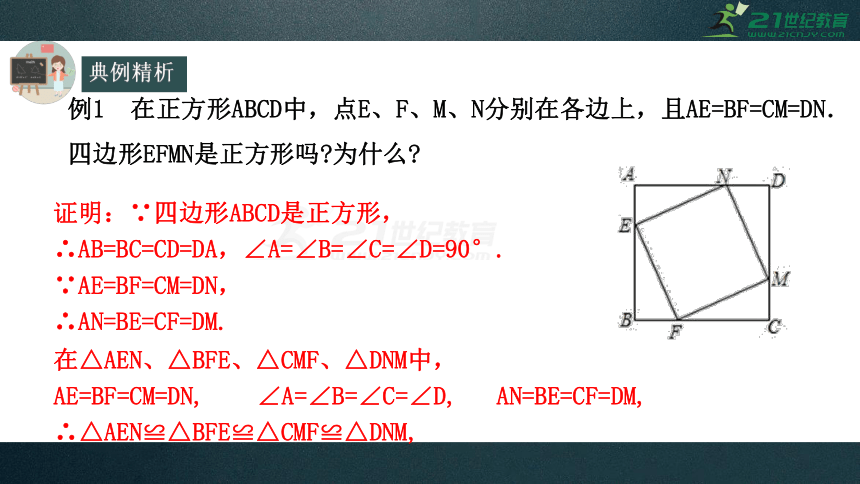
例1
在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.
四边形EFMN是正方形吗?为什么?
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
典例精析
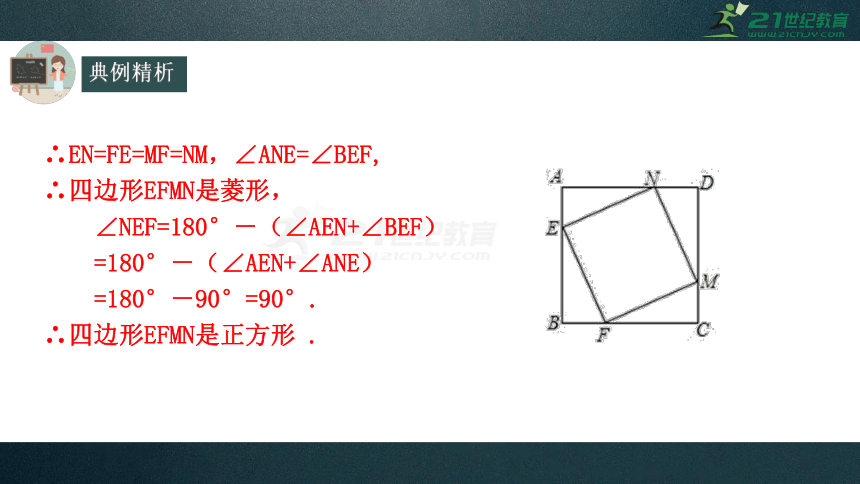
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形
.
小试牛刀
1.下列命题正确的是(
)
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线互相垂直平分的平行四边形是正方形
D.对角线相等的菱形是正方形
D
小试牛刀
2、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是(
)
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.
AO=CO,BO=DO,AB=BC
D.AO=BO=CO=DO,AC⊥BD
D
A
B
C
D
O
小试牛刀
3.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件____________________,可得出该四边形是正方形.
AB=BC(答案不唯一)
A
B
C
D
O
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________________(只填写序号).
②③或①④
小试牛刀
证明:∵
DE⊥AC,DF⊥AB
,
∴∠DEC=
∠DFC=90°.
又∵
∠C=90
°,∴四边形ADFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线,DE⊥AC,DG⊥AB,
∴
DE=DG.
同理得DG=DF,
∴ED=DF,
∴四边形ADFC是正方形.
5.如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
综合演练
1.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
综合演练
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,说明理由.
解:由四边形AEDF为正方形
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
综合演练
2.如图,在四边形ABCD中,
AB=BC
,对角线BD平分?ABC
,
P是BD上一点,过点P作PM?AD
,
PN?CD
,垂足分别为M、N.
(1)
求证:?ADB=?CDB;
(2)
若?ADC=90?,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(SAS).
∴∠ADB=∠CDB.
1
2
综合演练
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
综合演练
3.如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.
求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO
=45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,∴△CHO
≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
D
O
E
H
G
F
综合演练
∴OE=OG,OF=OH.
∴四边形EFGH为平行四边形
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO
,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
综合演练
4.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.(1)求证:BF=DE;(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB
,∠DAE=∠BAF
,AE=AF
,
∴△ADE≌△ABF(SAS),∴BF=DE;
综合演练
(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE=
AC,
∵AF=AE,∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴四边形
AFBE是平行四边形,
∵∠FAE=90°,AF=AE,∴四边形AFBE是正方形.
课堂小结
本节课你有哪些收获?
1、如何判断一个四边形是正方形?
2、你能绘制平行四边形、矩形、菱形的判定方法之间的关系吗?
课后作业
教材61页习题18.2第12题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
18.2.3正方形(2)
学习目标
1.探索并证明正方形的判定,并了解平行四边形、矩形、菱形之间的
联系和区别;(重点、难点)
2.会运用正方形的判定条件进行有关的论证和计算
.(难点)
回顾旧知
思考1:
正方形有哪些性质?
A
B
C
D
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
O
合作探究---正方形的判定
思考2:你是如何判断一个四边形是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
思考3:怎样判定一个四边形是正方形呢?
合作探究---正方形的判定
活动1
:
准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形.
正方形
想一想:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
合作探究---正方形的判定
活动2
把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
想一想:满足怎样条件的菱形是正方形?
正方形
一个角是直角
合作探究---正方形的判定
正方形的判定方法:
正方形
正方形
+
+
先判定菱形
先判定矩形
一个直角
一组邻边相等
典例精析
例1
在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.
四边形EFMN是正方形吗?为什么?
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
典例精析
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形
.
小试牛刀
1.下列命题正确的是(
)
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线互相垂直平分的平行四边形是正方形
D.对角线相等的菱形是正方形
D
小试牛刀
2、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是(
)
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.
AO=CO,BO=DO,AB=BC
D.AO=BO=CO=DO,AC⊥BD
D
A
B
C
D
O
小试牛刀
3.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件____________________,可得出该四边形是正方形.
AB=BC(答案不唯一)
A
B
C
D
O
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________________(只填写序号).
②③或①④
小试牛刀
证明:∵
DE⊥AC,DF⊥AB
,
∴∠DEC=
∠DFC=90°.
又∵
∠C=90
°,∴四边形ADFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线,DE⊥AC,DG⊥AB,
∴
DE=DG.
同理得DG=DF,
∴ED=DF,
∴四边形ADFC是正方形.
5.如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
综合演练
1.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
综合演练
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,说明理由.
解:由四边形AEDF为正方形
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
综合演练
2.如图,在四边形ABCD中,
AB=BC
,对角线BD平分?ABC
,
P是BD上一点,过点P作PM?AD
,
PN?CD
,垂足分别为M、N.
(1)
求证:?ADB=?CDB;
(2)
若?ADC=90?,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(SAS).
∴∠ADB=∠CDB.
1
2
综合演练
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
综合演练
3.如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.
求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO
=45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,∴△CHO
≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
D
O
E
H
G
F
综合演练
∴OE=OG,OF=OH.
∴四边形EFGH为平行四边形
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO
,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
综合演练
4.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.(1)求证:BF=DE;(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB
,∠DAE=∠BAF
,AE=AF
,
∴△ADE≌△ABF(SAS),∴BF=DE;
综合演练
(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE=
AC,
∵AF=AE,∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴四边形
AFBE是平行四边形,
∵∠FAE=90°,AF=AE,∴四边形AFBE是正方形.
课堂小结
本节课你有哪些收获?
1、如何判断一个四边形是正方形?
2、你能绘制平行四边形、矩形、菱形的判定方法之间的关系吗?
课后作业
教材61页习题18.2第12题.
https://www.21cnjy.com/help/help_extract.php
