【同步精讲】6.1 平方根与立方根(第1课时) 平方根 课件(共53张PPT)
文档属性
| 名称 | 【同步精讲】6.1 平方根与立方根(第1课时) 平方根 课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 19:08:02 | ||
图片预览











文档简介
(共53张PPT)
沪科版
初中数学
七年级下册
第六章《实数》
6.1
平方根
立方根
第1课时
平方根
对平方根和算术平方根进行理解分析,探究一般求法和意义,通过本节课的学习学生能够会求非负数的平方根与算术平方根会用计算器求一个数的平方根;结合习题进行举一反三强化训练,整体难度中等适合所有学生。
课堂学习要求
1.了解平方根及算术平方根的概念,会用根号表示
一个数的算术平方根;(重点)
2.会求非负数的平方根与算术平方根.(重点、难
点)
3.会用计算器求一个数的平方根;
教学目标及重难点
某家庭在装修儿童房时需铺地垫10.8m2,刚好用去正方形的地垫30块.
你能算出每块地垫的边长是多少吗?
?
导入新课
观察与思考
每块正方形地垫的面积是
10.8÷30=0.36(m2).
即
边长×边长=0.36.
由于
0.62=0.36,
因此面积为0.36m2的正方形地垫的边长是0.6m.
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25
dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
讲授新课
平方根的概念及其性质
一
问题引导
(1)若正方形画布的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2
1
9
16
36
100
正方形的边长/dm
都是已知一个数的平方,求这个数的问题.
1
3
4
6
10
填一填:
根据上述问题的共同点:已知一个数的平方,求这个数.由此我们抽象出下述概念:
一般地,如果有一个数的平方等于a,那么这个数叫作a的平方根,也叫作二次方根.
例如:由于22=4,(-2)2=4,所以4的平方根是2和-2
(可以合写为±2).
换句话说,如果
,那么x叫作a的平方根.
x2=a
一、平方根的概念
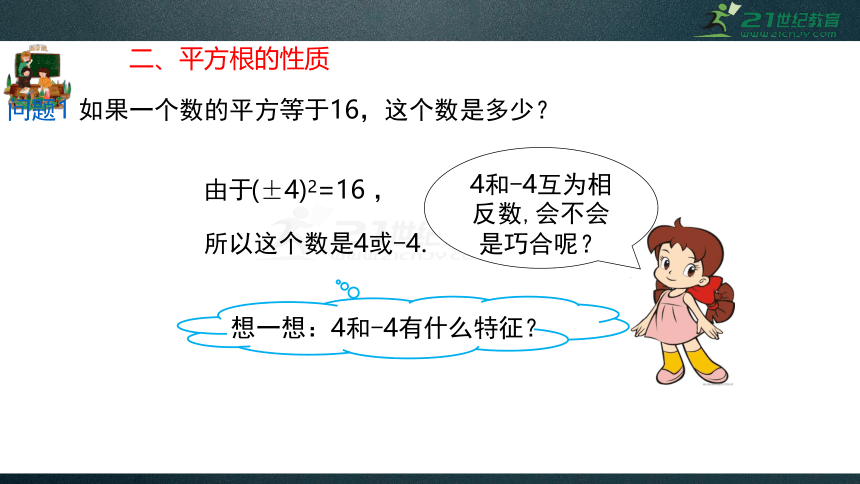
问题1
如果一个数的平方等于16,这个数是多少?
想一想:4和-4有什么特征?
4和-4互为相反数,会不会是巧合呢?
由于
,
所以这个数是4或-4.
(±4)2=16
二、平方根的性质
4
9
...
...
一个正数的平方根有两个,并且这两个数是相反数
合作与交流
观察所填的数据,填一填:
1的平方根是
;16的平方根是
,...
;
的平方根是
.
你发现了什么?
a2
±a
a2
±2
±3
±a
1.
144的平方根是什么?
2.
0的平方根是什么?
3.
的平方根是什么?
4.
-4有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
试一试
通过这些题目的解答,你能发现什么?
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
想一想
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
平方根的性质:
1.正数有两个平方根,两个平方根
互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
要点归纳
典例精析
例1
已知一个正数的两个平方根分别是2a-2和a-4,
则a的值是______.
解析:∵一个正数的两个平方根分别是2a-2和a-4,
∴2a-2+a-4=0,解得a=2.故答案为2.
一个正数有两个平方根,它们互为相反数.
归纳
这样,正数a的平方根可以用“
”来表示.
例如,4的平方根是2与-2,即
为书写方便,对正数a的平方根,我们有以下规定:
a的负平方根
记作
读作“负根号a”
a的正平方根
读作“根号a”
记作
三、平方根的数学符号表示
+1
-1
+2
-2
+3
-3
1
4
9
平方运算
我们知道已知一个数,求它的平方的运算叫作平方运算.
练一练:
四、开平方的概念
x
x2
+1
-1
+2
-2
+3
-3
1
4
9
?运算
那么已知一个数的平方,求这个数的运算叫作什么呢?
x
x2
开平方与平方互为逆运算,根据这种关系,可以求一个数的平方根.
求一个非负数的平方根的运算,叫作开平方.
特别规定:
典例精析
例2
求下列各数的平方根:
(1)64
;
(2)
(4)
(5)
11.
(3)0.0004;
解:(1)∵
,∴64的平方根为±8;
(2)∵
,∴
的平方根为
;
(3)∵
,∴0.0004的平方根为±0.02;
(4)∵
,∴
的平方根为
±25;
(5)11的平方根是
.
方法总结
运用平方运算求一个非负数的平方根是常用的方法,如被开方数是小数,要注意小数点的位置,也可先将小数化为分数,再求它的平方根,如被开方数是带分数,先要把它化为假分数.
注意:要弄清
,
,
的意义,
不能用来表示a的平方根,如:64的平方根不要写成
.
算术平方根的概念及性质
二
我们把正数a的正平方根
叫作a的算术平方根.
换句话说,
如果正数x满足:x2=a
,那么x叫作a的算术平方根.
a的算术平方根
记作
判断下列说法是否正确.
①25的算术平方根是5
(
);
②25的平方根是5
(
);
③5是25的平方根
(
).
√
√
注意区分“平方根”与“算术平方根”意义.
练一练:
例如:16的平方根是4和-4,其中4是16的算术平方根.
思考:正数、负数、0的算术平方根各有几个?
正数的算术平方根是一个正数,0的算术平方根还是0,负数没有算术平方根.
类似平方根的讨论,
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
算术平方根的性质
例3
分别求下列各数的算术平方根:
(1)100;
(2)
;
(3)0.49.
解
(1)由于102=100,因此
.
典例精析
(3)
由于0.72=0.49,因此
.
(2)由于42=
,因此
=4.
a(
)的算术平方根就是正平方根,且仅有一个
归纳
例4
若|m-1|
+
=0,求m+n的值.
解
因为|m-1|
≥0,
≥0,又|m-1|
+
=0,
所以
|m-1|
=0,
=0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
几个非负数的和为0,则每个数均为0,现阶段学过
的非负数有绝对值、一个数的平方及算术平方根.
归纳
3.若
,则a=
;
2.若
,则m=
;
4.若|a-3|+
,则代数式
=
.
1.若|a+3|=0
,
则a=
;
-3
7
5
-1
练一练
到目前为止,表示非负数的式子有:
a≥0,
|a|≥0,
a2
≥0,
≥0,
用计算器求平方根
三
用计算器求下列各式的值:
(1)
;
(2)
(精确到0.001).
解
(2)
依次按键
2
显示:1.414213562.
∴
.
(1)
依次按键
3136
显示:56.
∴
.
例5
随着“神舟”十号的升空,中国人又走出了探索宇宙
的一大步,但是你知道吗,要想围绕着地球旋转,飞
船的速度必须达到“第一宇宙速度”,其计算公式是
(单位:km/s,其中g=0.0098km/s2,为重力加
速度,R为6370km,为地球半径),请你求出第一宇宙速度的值(结果精确到0.01).
解
答:第一宇宙速度的值约为7.90km/s.
典例精析
将数据代入公式中,在用计算器直接求结果.
归纳
1.
判断下列说法是否正确.
正确.
(4)(-4)2的平方根是-4.
(1)
是
的一个平方根;
(2)
是6的算术平方根;
(3)
的值是±4;
正确.
不正确,是
4.
不正确,是
±4.
当堂练习
2.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是(
)
A.
a+1
B.
C.
a2+1
D.
D
解析:一个自然数的算术平方根是a,那么这个自然
数就是a2,下一个自然数就是a2+1,它的算术平方根
是
.
3.
分别求
64,6.25的平方根.并用式子表示
4.
分别求
81,0.16的算术平方根.
64的平方根是8与-
8,
.
6.25的平方根是2.5与-2.5
,
.
解
解
81的算术平方根是9,
.
0.16的算术平方根是0.4,
.
平方根的概念
正数的平方根
负数的平方根
0的平方根
正平方根
→
→
(没有)
(就是0本身)
负平方根
算术平方根
↑
课堂总结
https://www.21cnjy.com/help/help_extract.php
沪科版
初中数学
七年级下册
第六章《实数》
6.1
平方根
立方根
第1课时
平方根
对平方根和算术平方根进行理解分析,探究一般求法和意义,通过本节课的学习学生能够会求非负数的平方根与算术平方根会用计算器求一个数的平方根;结合习题进行举一反三强化训练,整体难度中等适合所有学生。
课堂学习要求
1.了解平方根及算术平方根的概念,会用根号表示
一个数的算术平方根;(重点)
2.会求非负数的平方根与算术平方根.(重点、难
点)
3.会用计算器求一个数的平方根;
教学目标及重难点
某家庭在装修儿童房时需铺地垫10.8m2,刚好用去正方形的地垫30块.
你能算出每块地垫的边长是多少吗?
?
导入新课
观察与思考
每块正方形地垫的面积是
10.8÷30=0.36(m2).
即
边长×边长=0.36.
由于
0.62=0.36,
因此面积为0.36m2的正方形地垫的边长是0.6m.
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25
dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
讲授新课
平方根的概念及其性质
一
问题引导
(1)若正方形画布的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2
1
9
16
36
100
正方形的边长/dm
都是已知一个数的平方,求这个数的问题.
1
3
4
6
10
填一填:
根据上述问题的共同点:已知一个数的平方,求这个数.由此我们抽象出下述概念:
一般地,如果有一个数的平方等于a,那么这个数叫作a的平方根,也叫作二次方根.
例如:由于22=4,(-2)2=4,所以4的平方根是2和-2
(可以合写为±2).
换句话说,如果
,那么x叫作a的平方根.
x2=a
一、平方根的概念
问题1
如果一个数的平方等于16,这个数是多少?
想一想:4和-4有什么特征?
4和-4互为相反数,会不会是巧合呢?
由于
,
所以这个数是4或-4.
(±4)2=16
二、平方根的性质
4
9
...
...
一个正数的平方根有两个,并且这两个数是相反数
合作与交流
观察所填的数据,填一填:
1的平方根是
;16的平方根是
,...
;
的平方根是
.
你发现了什么?
a2
±a
a2
±2
±3
±a
1.
144的平方根是什么?
2.
0的平方根是什么?
3.
的平方根是什么?
4.
-4有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
试一试
通过这些题目的解答,你能发现什么?
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
想一想
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
平方根的性质:
1.正数有两个平方根,两个平方根
互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
要点归纳
典例精析
例1
已知一个正数的两个平方根分别是2a-2和a-4,
则a的值是______.
解析:∵一个正数的两个平方根分别是2a-2和a-4,
∴2a-2+a-4=0,解得a=2.故答案为2.
一个正数有两个平方根,它们互为相反数.
归纳
这样,正数a的平方根可以用“
”来表示.
例如,4的平方根是2与-2,即
为书写方便,对正数a的平方根,我们有以下规定:
a的负平方根
记作
读作“负根号a”
a的正平方根
读作“根号a”
记作
三、平方根的数学符号表示
+1
-1
+2
-2
+3
-3
1
4
9
平方运算
我们知道已知一个数,求它的平方的运算叫作平方运算.
练一练:
四、开平方的概念
x
x2
+1
-1
+2
-2
+3
-3
1
4
9
?运算
那么已知一个数的平方,求这个数的运算叫作什么呢?
x
x2
开平方与平方互为逆运算,根据这种关系,可以求一个数的平方根.
求一个非负数的平方根的运算,叫作开平方.
特别规定:
典例精析
例2
求下列各数的平方根:
(1)64
;
(2)
(4)
(5)
11.
(3)0.0004;
解:(1)∵
,∴64的平方根为±8;
(2)∵
,∴
的平方根为
;
(3)∵
,∴0.0004的平方根为±0.02;
(4)∵
,∴
的平方根为
±25;
(5)11的平方根是
.
方法总结
运用平方运算求一个非负数的平方根是常用的方法,如被开方数是小数,要注意小数点的位置,也可先将小数化为分数,再求它的平方根,如被开方数是带分数,先要把它化为假分数.
注意:要弄清
,
,
的意义,
不能用来表示a的平方根,如:64的平方根不要写成
.
算术平方根的概念及性质
二
我们把正数a的正平方根
叫作a的算术平方根.
换句话说,
如果正数x满足:x2=a
,那么x叫作a的算术平方根.
a的算术平方根
记作
判断下列说法是否正确.
①25的算术平方根是5
(
);
②25的平方根是5
(
);
③5是25的平方根
(
).
√
√
注意区分“平方根”与“算术平方根”意义.
练一练:
例如:16的平方根是4和-4,其中4是16的算术平方根.
思考:正数、负数、0的算术平方根各有几个?
正数的算术平方根是一个正数,0的算术平方根还是0,负数没有算术平方根.
类似平方根的讨论,
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
算术平方根的性质
例3
分别求下列各数的算术平方根:
(1)100;
(2)
;
(3)0.49.
解
(1)由于102=100,因此
.
典例精析
(3)
由于0.72=0.49,因此
.
(2)由于42=
,因此
=4.
a(
)的算术平方根就是正平方根,且仅有一个
归纳
例4
若|m-1|
+
=0,求m+n的值.
解
因为|m-1|
≥0,
≥0,又|m-1|
+
=0,
所以
|m-1|
=0,
=0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
几个非负数的和为0,则每个数均为0,现阶段学过
的非负数有绝对值、一个数的平方及算术平方根.
归纳
3.若
,则a=
;
2.若
,则m=
;
4.若|a-3|+
,则代数式
=
.
1.若|a+3|=0
,
则a=
;
-3
7
5
-1
练一练
到目前为止,表示非负数的式子有:
a≥0,
|a|≥0,
a2
≥0,
≥0,
用计算器求平方根
三
用计算器求下列各式的值:
(1)
;
(2)
(精确到0.001).
解
(2)
依次按键
2
显示:1.414213562.
∴
.
(1)
依次按键
3136
显示:56.
∴
.
例5
随着“神舟”十号的升空,中国人又走出了探索宇宙
的一大步,但是你知道吗,要想围绕着地球旋转,飞
船的速度必须达到“第一宇宙速度”,其计算公式是
(单位:km/s,其中g=0.0098km/s2,为重力加
速度,R为6370km,为地球半径),请你求出第一宇宙速度的值(结果精确到0.01).
解
答:第一宇宙速度的值约为7.90km/s.
典例精析
将数据代入公式中,在用计算器直接求结果.
归纳
1.
判断下列说法是否正确.
正确.
(4)(-4)2的平方根是-4.
(1)
是
的一个平方根;
(2)
是6的算术平方根;
(3)
的值是±4;
正确.
不正确,是
4.
不正确,是
±4.
当堂练习
2.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是(
)
A.
a+1
B.
C.
a2+1
D.
D
解析:一个自然数的算术平方根是a,那么这个自然
数就是a2,下一个自然数就是a2+1,它的算术平方根
是
.
3.
分别求
64,6.25的平方根.并用式子表示
4.
分别求
81,0.16的算术平方根.
64的平方根是8与-
8,
.
6.25的平方根是2.5与-2.5
,
.
解
解
81的算术平方根是9,
.
0.16的算术平方根是0.4,
.
平方根的概念
正数的平方根
负数的平方根
0的平方根
正平方根
→
→
(没有)
(就是0本身)
负平方根
算术平方根
↑
课堂总结
https://www.21cnjy.com/help/help_extract.php
