2020--2021学年-沪科版八年级数学下册课件-19.1 多边形内角和(20张)
文档属性
| 名称 | 2020--2021学年-沪科版八年级数学下册课件-19.1 多边形内角和(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 382.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 00:23:09 | ||
图片预览


文档简介
19.1 多边形内角和
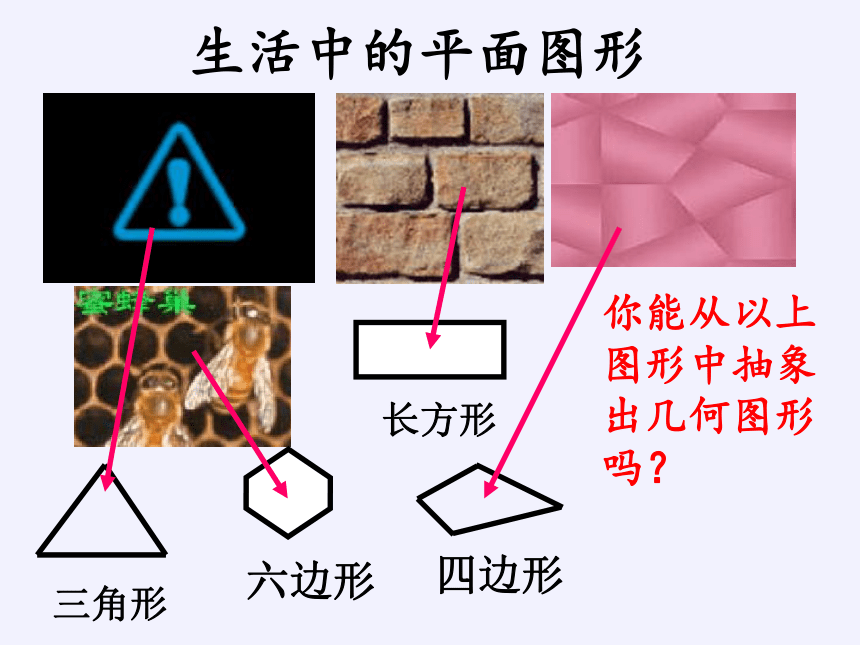
生活中的平面图形
三角形
长方形
四边形
六边形
你能从以上图形中抽象出几何图形吗?
自主学习要求:
1:类比三角形的概念,自主学习多边形的有关概念:边、顶点、内角、外角、多边形的命名以及对角线。
2:学会区分凸多边形和凹多边形。
类比推理,得出概念
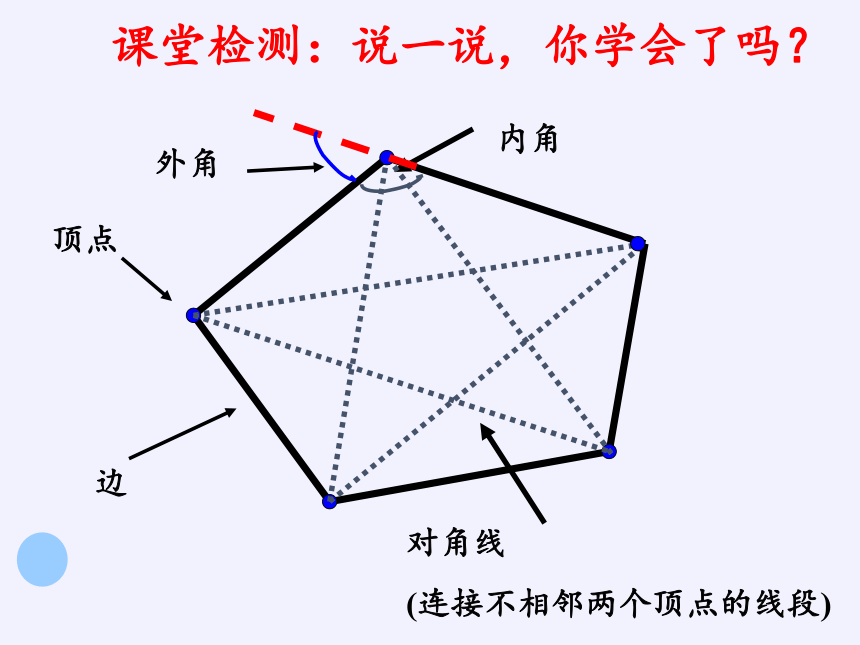
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
外角
课堂检测:说一说,你学会了吗?
四边形
五边形
六边形
八边形
……
A
B
D
C
B
A
D
C
F
E
D
C
B
A
E
A
H
G
F
E
D
C
B
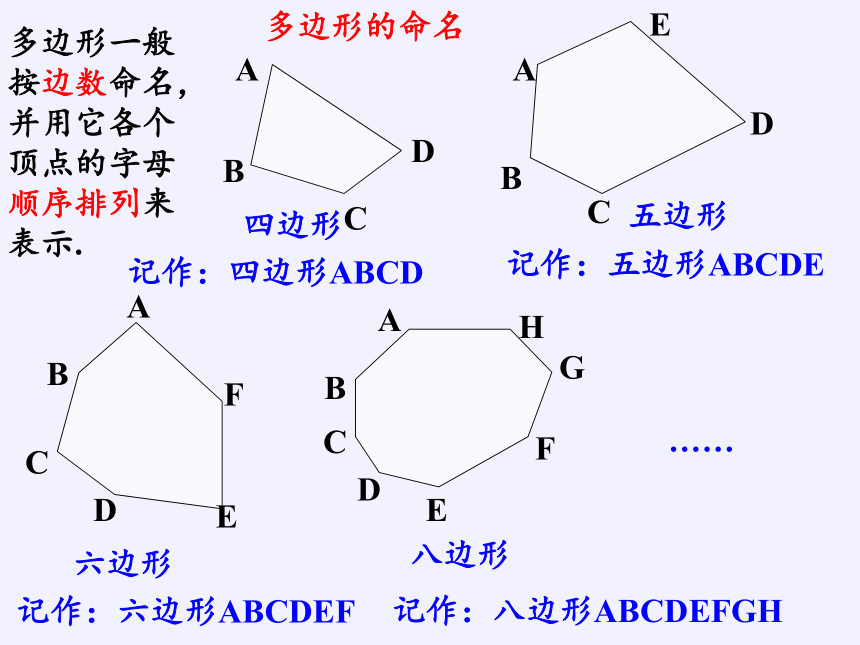
记作:四边形ABCD
记作:五边形ABCDE
记作:六边形ABCDEF
记作:八边形ABCDEFGH
多边形的命名
多边形一般按边数命名,并用它各个顶点的字母顺序排列来表示.
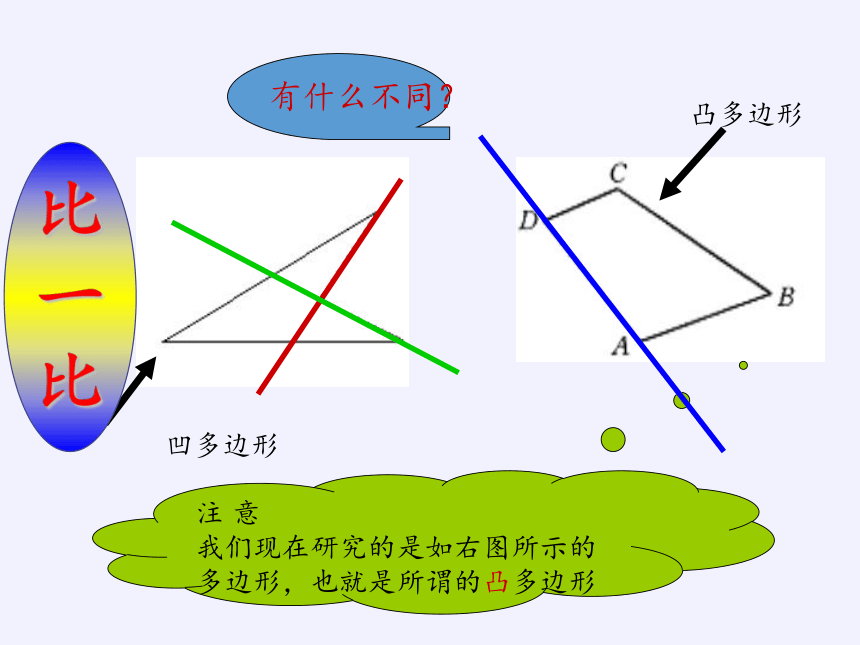
注 意
我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形
有什么不同?
凹多边形
凸多边形
比
一
比
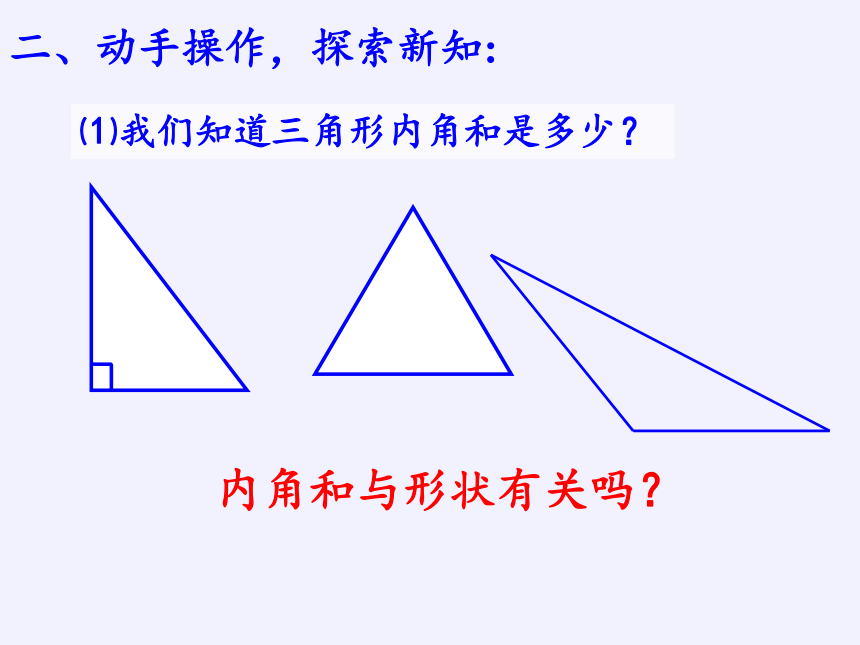
⑴我们知道三角形内角和是多少?
内角和与形状有关吗?
二、动手操作,探索新知:
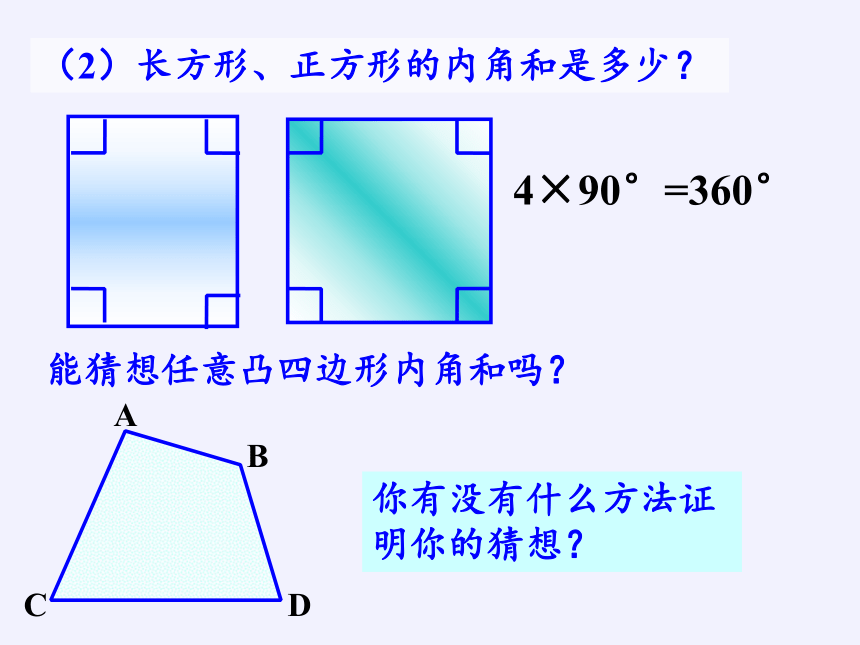
(2)长方形、正方形的内角和是多少?
4×90°=360°
能猜想任意凸四边形内角和吗?
A
B
C
D
你有没有什么方法证明你的猜想?
自
己
动
手
A
B
C
D
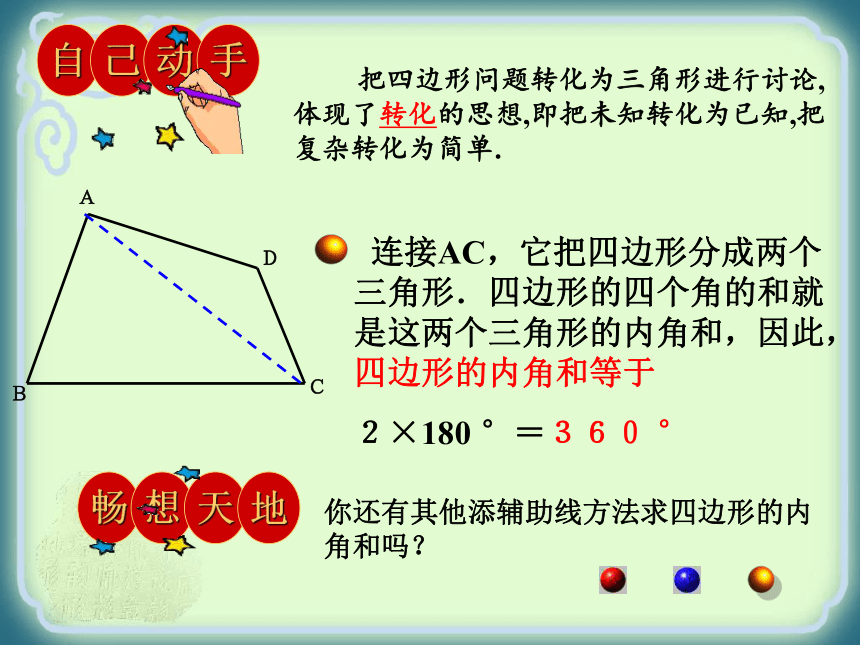
连接AC,它把四边形分成两个三角形.四边形的四个角的和就是这两个三角形的内角和,因此,四边形的内角和等于
2×180 °=360 °
你还有其他添辅助线方法求四边形的内角和吗?
畅
想
天
地
把四边形问题转化为三角形进行讨论,体现了转化的思想,即把未知转化为已知,把复杂转化为简单.
A
D
B
C
D
B
C
A
D
B
A
B
C
D
1
2
3
1
2
3
B
C
A
D
1
2
3
4
2
1
3
4
方法一:由多边形一个顶点引对角线分割三角形
方法二:在多边形一条边上任取一点分割三角形
方法三:在多边形内部任取一点分割三角形
A
B
C
D
E
想一想
这个五边形的内角和呢?
180°× 3 = 540°
你能动手做一做吗?
五边形的内角和等于540°
按照第一种分割的做法来看:
归纳总结
多边形边数
从一个顶点引出对角线数
图形
分割成的三角形个数
多边形的内角和
4
5
6
...
……
……
……
……
n
2
2×180°
3
3×180°
4
4×180°
n-2
(n-2)×180°
1
2
3
n-3
定理:n边形的内角和等于
(n-2)? 180°
(n为不小于3的整数)
我学习,我归纳
1、求十边形的内角和的度数。
2、若一个多边形的内角和是1080°,求这个多边形的边数。
解:(10-2)×180°
=1440°
答:十边形的内角和为1440°。
知识应用
解:设这个多边形的边数为n,
可列方程(n-2)×180°= 1080°.
解得n=8
答:这个多边形是八边形。
2、如图:
(1)作多边形所有过顶点A的对角线,并分别用字母表达出来。
(2)求这个多边形的内角和。
A
B
C
D
E
F
解(1)过顶点A的对角线共有三 条,分别是AC、AD和AE .
(2)这个多边形的内角和是:(6-2) · 180° = 720°
三、当堂训练,巩固基础:
1、填空:
(1)一个n边形有 个顶点, 条边, 个内角, 个外角,从一个顶点出发,能引 条对角线。
(2) 多边形的边数每多一条,它的内角和就增加 .
n
n
n
n
n - 3
180°
3.
若n边形的内角和是144n°,那么n= .
10
解:设这个多边形的边数为n:
(n - 2) · 180° = 144n°
n = 10
4、在四边形ABCD中,∠A=120°,
∠B:∠C:∠D = 3:4:5.求∠B,∠C,∠D的度数。
提升练习
4、在四边形ABCD中,∠A=120°,∠B:∠C:∠D = 3:4:5.求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x, 4x , 5x 度,由四边形的内角和等于360°可得:
120 + 3x + 4x + 5x = 360
整理,得 12x = 240
解方程,得 x = 20
∴ 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D分别为60°,80°, 100°.
①
②
③
A
B
C
D
E
F
M
N
有一把锋利的“小刀”,把你的课桌(四边形)一个角削去,剩下的课桌是一个几边形?
它的内角和是多少?
课堂小结
(1)通过本节课的学习,你学到了哪些知识和方法?
(2)你认为这节课中最大的收获是什么?
(3)你还有哪些疑惑或不足?
知识:
多边形的有关概念;
多边形内角和公式;
方法:
类比,转化,归纳
作业:1、习题19.1
谢 谢
生活中的平面图形
三角形
长方形
四边形
六边形
你能从以上图形中抽象出几何图形吗?
自主学习要求:
1:类比三角形的概念,自主学习多边形的有关概念:边、顶点、内角、外角、多边形的命名以及对角线。
2:学会区分凸多边形和凹多边形。
类比推理,得出概念
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
外角
课堂检测:说一说,你学会了吗?
四边形
五边形
六边形
八边形
……
A
B
D
C
B
A
D
C
F
E
D
C
B
A
E
A
H
G
F
E
D
C
B
记作:四边形ABCD
记作:五边形ABCDE
记作:六边形ABCDEF
记作:八边形ABCDEFGH
多边形的命名
多边形一般按边数命名,并用它各个顶点的字母顺序排列来表示.
注 意
我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形
有什么不同?
凹多边形
凸多边形
比
一
比
⑴我们知道三角形内角和是多少?
内角和与形状有关吗?
二、动手操作,探索新知:
(2)长方形、正方形的内角和是多少?
4×90°=360°
能猜想任意凸四边形内角和吗?
A
B
C
D
你有没有什么方法证明你的猜想?
自
己
动
手
A
B
C
D
连接AC,它把四边形分成两个三角形.四边形的四个角的和就是这两个三角形的内角和,因此,四边形的内角和等于
2×180 °=360 °
你还有其他添辅助线方法求四边形的内角和吗?
畅
想
天
地
把四边形问题转化为三角形进行讨论,体现了转化的思想,即把未知转化为已知,把复杂转化为简单.
A
D
B
C
D
B
C
A
D
B
A
B
C
D
1
2
3
1
2
3
B
C
A
D
1
2
3
4
2
1
3
4
方法一:由多边形一个顶点引对角线分割三角形
方法二:在多边形一条边上任取一点分割三角形
方法三:在多边形内部任取一点分割三角形
A
B
C
D
E
想一想
这个五边形的内角和呢?
180°× 3 = 540°
你能动手做一做吗?
五边形的内角和等于540°
按照第一种分割的做法来看:
归纳总结
多边形边数
从一个顶点引出对角线数
图形
分割成的三角形个数
多边形的内角和
4
5
6
...
……
……
……
……
n
2
2×180°
3
3×180°
4
4×180°
n-2
(n-2)×180°
1
2
3
n-3
定理:n边形的内角和等于
(n-2)? 180°
(n为不小于3的整数)
我学习,我归纳
1、求十边形的内角和的度数。
2、若一个多边形的内角和是1080°,求这个多边形的边数。
解:(10-2)×180°
=1440°
答:十边形的内角和为1440°。
知识应用
解:设这个多边形的边数为n,
可列方程(n-2)×180°= 1080°.
解得n=8
答:这个多边形是八边形。
2、如图:
(1)作多边形所有过顶点A的对角线,并分别用字母表达出来。
(2)求这个多边形的内角和。
A
B
C
D
E
F
解(1)过顶点A的对角线共有三 条,分别是AC、AD和AE .
(2)这个多边形的内角和是:(6-2) · 180° = 720°
三、当堂训练,巩固基础:
1、填空:
(1)一个n边形有 个顶点, 条边, 个内角, 个外角,从一个顶点出发,能引 条对角线。
(2) 多边形的边数每多一条,它的内角和就增加 .
n
n
n
n
n - 3
180°
3.
若n边形的内角和是144n°,那么n= .
10
解:设这个多边形的边数为n:
(n - 2) · 180° = 144n°
n = 10
4、在四边形ABCD中,∠A=120°,
∠B:∠C:∠D = 3:4:5.求∠B,∠C,∠D的度数。
提升练习
4、在四边形ABCD中,∠A=120°,∠B:∠C:∠D = 3:4:5.求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x, 4x , 5x 度,由四边形的内角和等于360°可得:
120 + 3x + 4x + 5x = 360
整理,得 12x = 240
解方程,得 x = 20
∴ 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D分别为60°,80°, 100°.
①
②
③
A
B
C
D
E
F
M
N
有一把锋利的“小刀”,把你的课桌(四边形)一个角削去,剩下的课桌是一个几边形?
它的内角和是多少?
课堂小结
(1)通过本节课的学习,你学到了哪些知识和方法?
(2)你认为这节课中最大的收获是什么?
(3)你还有哪些疑惑或不足?
知识:
多边形的有关概念;
多边形内角和公式;
方法:
类比,转化,归纳
作业:1、习题19.1
谢 谢
