五年级数学下册试题 一课一练《因数与倍数--质数和合数》习题-苏教版(含答案)
文档属性
| 名称 | 五年级数学下册试题 一课一练《因数与倍数--质数和合数》习题-苏教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 286.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 08:18:25 | ||
图片预览



文档简介
《因数与倍数--质数和合数》习题
一.选择题
1、下面表示分解质因数正确的是
A.
B.
C.
D.
2、在下面四组数中, 组中的数都是质数.
A.13,21,17
B.91,71,51
C.43,53,73
D.17,37,85
3、一个合数至少有 个因数.
A.1
B.2
C.3
D.无数
4、 的积是质数.
A.1
B.可以是1,也可以是别的数
C.质数
5、3个质数相加,结果
A.一定是奇数
B.一定是偶数
C.可能是奇数也可能是偶数
6、把78分解质因数是
A.
B.
C.
7、把24分解质因数,下面的式子中,正确的是
A.
B.
C.
8、下面四个数中, 是合数.
二、填空题
9、在18的所有因数中,质数有 ,合数有 .
10、在连续的自然数中,两个都是质数的是
和
.
11、最小的质数是
,它与最小的合数的和是
.
12、从0,1,2,3四个数中,任选三个数字,组成一个同时是2和5的倍数,又含有因数3的最大三位数是 ,把它分解质因数是 .
13、两个质数的和是15,积是26,这两个质数分别是 和 .
14、一个数的最小倍数是48,把这个数分解质因数是 .
三、判断题
15、边长是质数的正方形,它的周长一定是合数. (判断对错)
16、自然数中,最小的质数与最小的合数相差2.
.
(判断对错)
17、两个质数相乘,积是合数.
(判断对错)
18、把一个数用质数相乘的形式表示出来,叫做分解质因数. (判断对错)
19、两个不同数相乘的积一定是合数. (判断对错)
四、应用题
20、有三张写有数字7,8,9的卡片,从中抽取一张、两张、三张,分别组成一位数、两位数和三位数,其中哪些是质数?哪些是合数?
21、有三个小朋友的年龄正好是三个连续自然数,且他们年龄之积是210,这三个小朋友年龄分别是多少?
五、操作题
22、先圈出下面的合数,再把它们分解质因数.
23、送信,连一连.
24、下面各数中哪些是质数?哪些是合数?分别填入指定的圈里.
17、37、40、51、1、61、22、73、83、95、11、15、99、87
六、解答题
25、两个质数的乘积是91,这两个质数分别是多少?
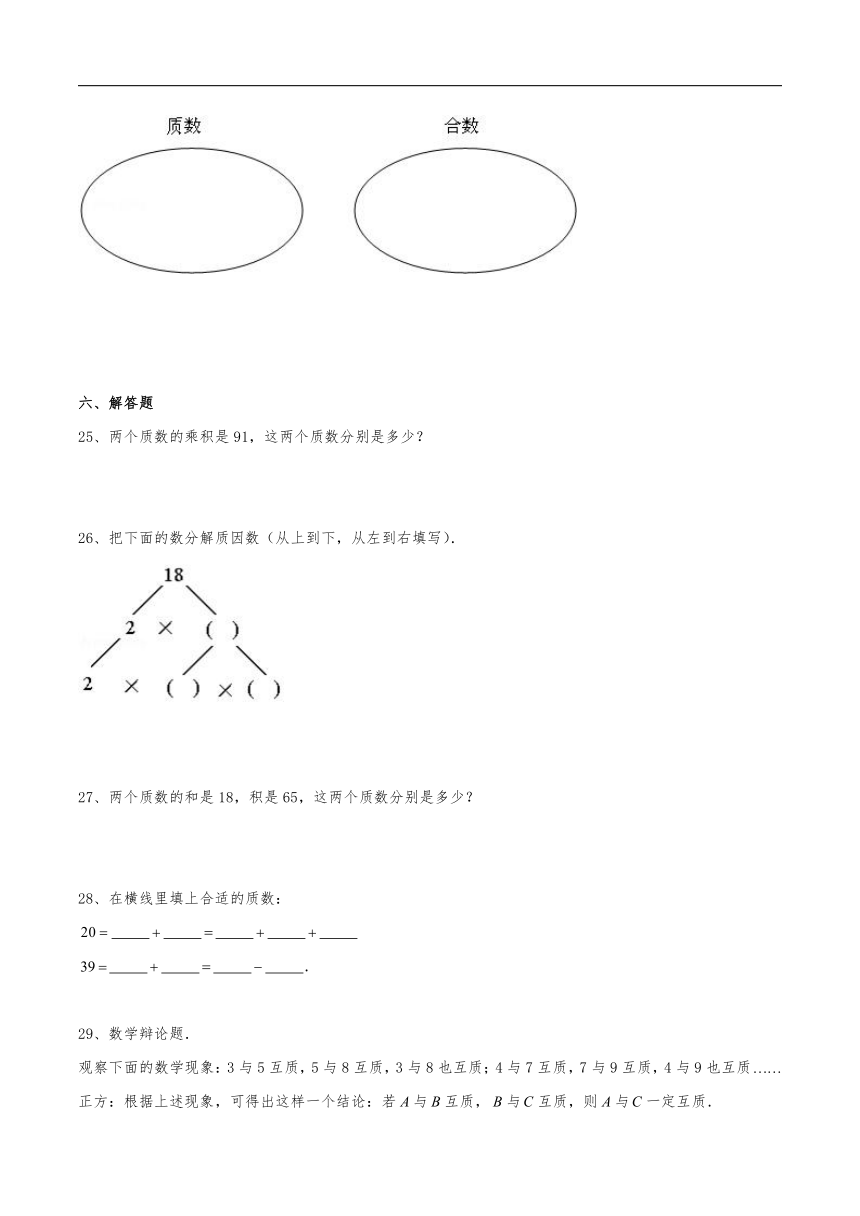
26、把下面的数分解质因数(从上到下,从左到右填写).
27、两个质数的和是18,积是65,这两个质数分别是多少?
28、在横线里填上合适的质数:
.
29、数学辩论题.
观察下面的数学现象:3与5互质,5与8互质,3与8也互质;4与7互质,7与9互质,4与9也互质正方:根据上述现象,可得出这样一个结论:若与互质,与互质,则与一定互质.
你(作为反方)是否认同正方观点?如果不同意,请举例予以辩论.
30、将下面合数分解质因数.
(1)26
(2)18
(3)24
(4)35
31、在11、18、33中,
是质数,
是
的质因数,
和
是互质数.
32、一个数的最大约数是42,把这个数分解质因数是
.
答案
一、选择题
1、解:、,不符合分解质因数的书写形式.
、,其中1既不是质数,也不是合数,所以不正确;
、,其中1既不是质数,也不是合数,所以不正确;
、,符合要求,所以正确;
故选:.
2、解:组中21是合数;
组中91、71、51都是合数;
组中43、53、73都是质数;
组中85是合数.
故选:.
3、解:一个合数至少有3个因数.
故选:.
4、解:,37还是质数,所以的积是质数;
故选:.
5、解:根据数和的奇偶性可知,两个质数的合可能是奇数,也可能是偶数;奇数中包含质数,偶数中除2之外全为合数,例如,10是偶数,,15是奇数,所以,3个质数相加,结果可能是奇数也可能是偶数;
故选:.
6、解:
故选:.
7、解:.
故选:.
8、解:83、97都仅有1和它本身两个因素所以是质数;
51有因数1、3、17、51;
119有因数1、7、17、119.
所以51、119是合数.
故选:、.
二、填空题
9、解:18的因数有:1,2,3,6,9,18.
其中2,3为质数,即其中有2个质数,6、9、18为合数,即有3个合数.
故答案为:2、3、6、9、18.
10、解:在连续的自然数中,两个都是质数的只有2和3.
故答案为:2、3.
11、解:最小的质数是2,最小的合数是4,它们的和是;
故答案为:2,6.
12、解:符合条件的三位数有120、210,其中最大三位数是210;
故答案为:210,.
13、解:
所以,这两个质数是2,13.
故答案为:2,13.
14、解:一个数的最大因数和最小最小倍数都是它本身,所以这个数是48,
;
故答案为:.
三、判断题
15、解:正方形的周长边长;
它的周长至少有三个约数:1,4,边长,所以说一定是合数;
边长是质数的正方形,它的周长一定是合数,所以本题说法正确;
故答案为:.
16、解:在自然数中最小的质数是2,最小的合数是4,
最小的质数与最小的合数相差:,
所以原题说法正确;
故答案为:.
17、解:质数质数积,
积是两个质数的倍数,这两个质数也就是这个积的因数,
这样积的因数除了1和它本身外还有这两个质数,
所以它们的积一定是合数;
故答案为:.
18、解:把一个数用质数相乘的形式表示出来,叫做分解质因数是正确的.
故答案为:.
19、解;1和2是大于零的自然数,它们的积,2是质数,1和5是大于零的自然数,它们的积,5是质数,
所以两个不同数相乘的积一定是合数的说法是错误的;
故答案为:.
四、应用题
20、解;三张数字卡片7、8、9,
从中抽一张,分别组成的一位数是7、8、9;
从中抽两张组成的两位数有:78、79、87、89、97、98,
从中抽三张组成的三位数有:789、798、879、897、987、978;
其中质数有:7、79、89、97;合数有:8、9、78、87、98、789、798、879、897、987、978.
21、解:因为;
所以这三个自然数分别是5、6、7.
答:这三个小朋友年龄分别是5,6,7.
五、操作题
22、解:如图所示:
23、解:
24、解:质数有:17、37、61、73、83、11;
合数有:40、51、22、95、15、99、87.
故答案为:
六、解答题
25、解:因为,
所以这两个质数分别是7、13.
答:这两个质数分别是7和13.
26、解:
故完成填空如下:
27、解:把65分解质因数:
,
答:这两个质数是5和13.
28、解:根据质数的意义可知,
,
.
故答案为:3,17,2,5,13;2,37,41,2.
29、解:若与互质,与互质,则与不一定互质,
例如:3与5互质,5与9互质,但3与9不互质,3和9的公因数有:1、3.
30、解:(1);
(2);
(3);
(4);
故答案为:;;;.
31、解:在11、18、33中,11是质数,11是33的质因数,11和18是互质数.
故答案为:11,11,33,11,18.
32、解:
故答案为:.
一.选择题
1、下面表示分解质因数正确的是
A.
B.
C.
D.
2、在下面四组数中, 组中的数都是质数.
A.13,21,17
B.91,71,51
C.43,53,73
D.17,37,85
3、一个合数至少有 个因数.
A.1
B.2
C.3
D.无数
4、 的积是质数.
A.1
B.可以是1,也可以是别的数
C.质数
5、3个质数相加,结果
A.一定是奇数
B.一定是偶数
C.可能是奇数也可能是偶数
6、把78分解质因数是
A.
B.
C.
7、把24分解质因数,下面的式子中,正确的是
A.
B.
C.
8、下面四个数中, 是合数.
二、填空题
9、在18的所有因数中,质数有 ,合数有 .
10、在连续的自然数中,两个都是质数的是
和
.
11、最小的质数是
,它与最小的合数的和是
.
12、从0,1,2,3四个数中,任选三个数字,组成一个同时是2和5的倍数,又含有因数3的最大三位数是 ,把它分解质因数是 .
13、两个质数的和是15,积是26,这两个质数分别是 和 .
14、一个数的最小倍数是48,把这个数分解质因数是 .
三、判断题
15、边长是质数的正方形,它的周长一定是合数. (判断对错)
16、自然数中,最小的质数与最小的合数相差2.
.
(判断对错)
17、两个质数相乘,积是合数.
(判断对错)
18、把一个数用质数相乘的形式表示出来,叫做分解质因数. (判断对错)
19、两个不同数相乘的积一定是合数. (判断对错)
四、应用题
20、有三张写有数字7,8,9的卡片,从中抽取一张、两张、三张,分别组成一位数、两位数和三位数,其中哪些是质数?哪些是合数?
21、有三个小朋友的年龄正好是三个连续自然数,且他们年龄之积是210,这三个小朋友年龄分别是多少?
五、操作题
22、先圈出下面的合数,再把它们分解质因数.
23、送信,连一连.
24、下面各数中哪些是质数?哪些是合数?分别填入指定的圈里.
17、37、40、51、1、61、22、73、83、95、11、15、99、87
六、解答题
25、两个质数的乘积是91,这两个质数分别是多少?
26、把下面的数分解质因数(从上到下,从左到右填写).
27、两个质数的和是18,积是65,这两个质数分别是多少?
28、在横线里填上合适的质数:
.
29、数学辩论题.
观察下面的数学现象:3与5互质,5与8互质,3与8也互质;4与7互质,7与9互质,4与9也互质正方:根据上述现象,可得出这样一个结论:若与互质,与互质,则与一定互质.
你(作为反方)是否认同正方观点?如果不同意,请举例予以辩论.
30、将下面合数分解质因数.
(1)26
(2)18
(3)24
(4)35
31、在11、18、33中,
是质数,
是
的质因数,
和
是互质数.
32、一个数的最大约数是42,把这个数分解质因数是
.
答案
一、选择题
1、解:、,不符合分解质因数的书写形式.
、,其中1既不是质数,也不是合数,所以不正确;
、,其中1既不是质数,也不是合数,所以不正确;
、,符合要求,所以正确;
故选:.
2、解:组中21是合数;
组中91、71、51都是合数;
组中43、53、73都是质数;
组中85是合数.
故选:.
3、解:一个合数至少有3个因数.
故选:.
4、解:,37还是质数,所以的积是质数;
故选:.
5、解:根据数和的奇偶性可知,两个质数的合可能是奇数,也可能是偶数;奇数中包含质数,偶数中除2之外全为合数,例如,10是偶数,,15是奇数,所以,3个质数相加,结果可能是奇数也可能是偶数;
故选:.
6、解:
故选:.
7、解:.
故选:.
8、解:83、97都仅有1和它本身两个因素所以是质数;
51有因数1、3、17、51;
119有因数1、7、17、119.
所以51、119是合数.
故选:、.
二、填空题
9、解:18的因数有:1,2,3,6,9,18.
其中2,3为质数,即其中有2个质数,6、9、18为合数,即有3个合数.
故答案为:2、3、6、9、18.
10、解:在连续的自然数中,两个都是质数的只有2和3.
故答案为:2、3.
11、解:最小的质数是2,最小的合数是4,它们的和是;
故答案为:2,6.
12、解:符合条件的三位数有120、210,其中最大三位数是210;
故答案为:210,.
13、解:
所以,这两个质数是2,13.
故答案为:2,13.
14、解:一个数的最大因数和最小最小倍数都是它本身,所以这个数是48,
;
故答案为:.
三、判断题
15、解:正方形的周长边长;
它的周长至少有三个约数:1,4,边长,所以说一定是合数;
边长是质数的正方形,它的周长一定是合数,所以本题说法正确;
故答案为:.
16、解:在自然数中最小的质数是2,最小的合数是4,
最小的质数与最小的合数相差:,
所以原题说法正确;
故答案为:.
17、解:质数质数积,
积是两个质数的倍数,这两个质数也就是这个积的因数,
这样积的因数除了1和它本身外还有这两个质数,
所以它们的积一定是合数;
故答案为:.
18、解:把一个数用质数相乘的形式表示出来,叫做分解质因数是正确的.
故答案为:.
19、解;1和2是大于零的自然数,它们的积,2是质数,1和5是大于零的自然数,它们的积,5是质数,
所以两个不同数相乘的积一定是合数的说法是错误的;
故答案为:.
四、应用题
20、解;三张数字卡片7、8、9,
从中抽一张,分别组成的一位数是7、8、9;
从中抽两张组成的两位数有:78、79、87、89、97、98,
从中抽三张组成的三位数有:789、798、879、897、987、978;
其中质数有:7、79、89、97;合数有:8、9、78、87、98、789、798、879、897、987、978.
21、解:因为;
所以这三个自然数分别是5、6、7.
答:这三个小朋友年龄分别是5,6,7.
五、操作题
22、解:如图所示:
23、解:
24、解:质数有:17、37、61、73、83、11;
合数有:40、51、22、95、15、99、87.
故答案为:
六、解答题
25、解:因为,
所以这两个质数分别是7、13.
答:这两个质数分别是7和13.
26、解:
故完成填空如下:
27、解:把65分解质因数:
,
答:这两个质数是5和13.
28、解:根据质数的意义可知,
,
.
故答案为:3,17,2,5,13;2,37,41,2.
29、解:若与互质,与互质,则与不一定互质,
例如:3与5互质,5与9互质,但3与9不互质,3和9的公因数有:1、3.
30、解:(1);
(2);
(3);
(4);
故答案为:;;;.
31、解:在11、18、33中,11是质数,11是33的质因数,11和18是互质数.
故答案为:11,11,33,11,18.
32、解:
故答案为:.
