安徽省桐城市龙河初中2020——2021学年 九年级上学期数学期末训练五(word含答案)
文档属性
| 名称 | 安徽省桐城市龙河初中2020——2021学年 九年级上学期数学期末训练五(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 22:54:27 | ||
图片预览



文档简介
安徽省桐城市龙河初中2020-2021学年沪科版九年级上学期数学期末训练五
一、选择题(本大题共10小题,每小题3分,共30分)
1.方程(x+1)(x-2)=x+1的解是(
)
A.2
B.3
C.-1,2
D.-1,3
2.在单词NAME的四个字母中,是中心对称图形的是(
)
A.N
B.A
C.M
D.E
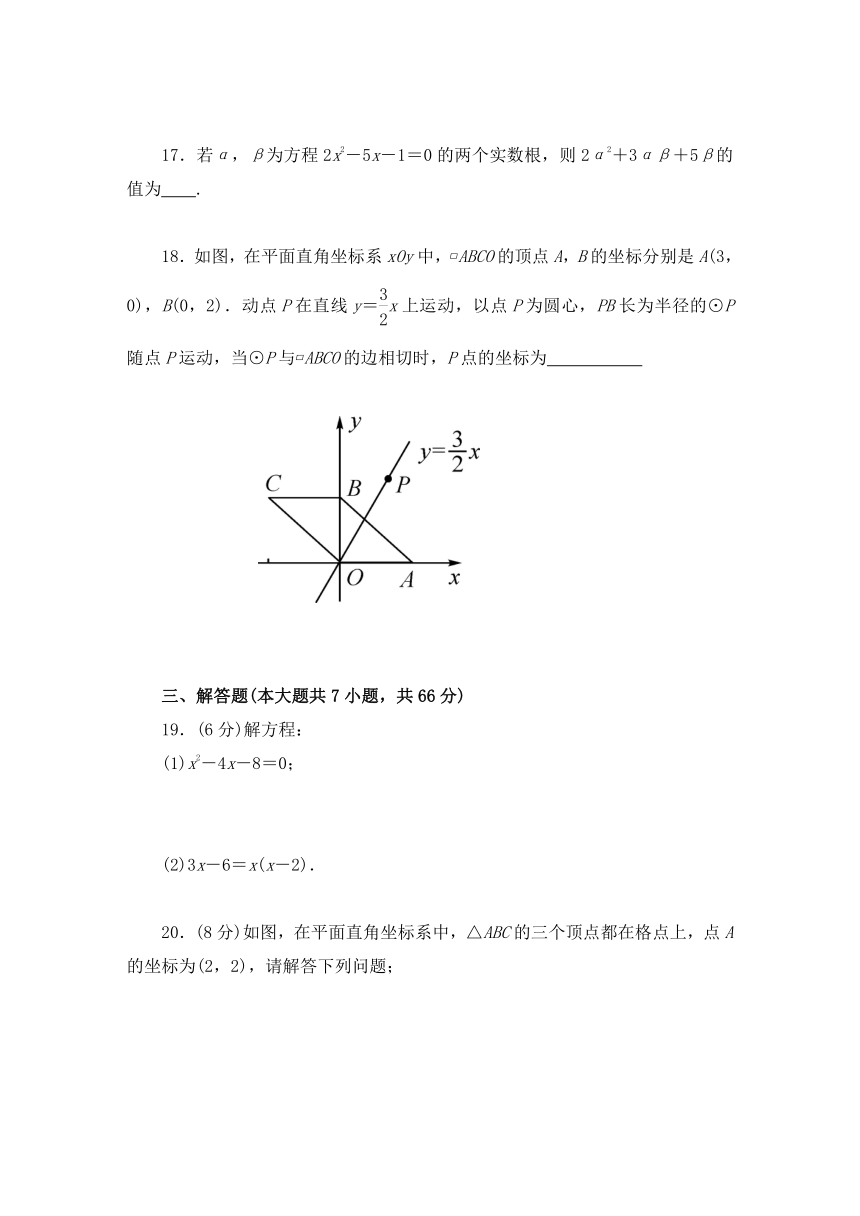
3.(2018·宜昌)如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为(
)
A.30°
B.35°
C.40°
D.45°
第3题图 第7题图
第8题图
4.将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为(
)
A.y=(x-1)2+3
B.y=(x+1)2+3
C.y=(x-1)2-3
D.y=(x+1)2-3
5.关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是(
)
6.若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是(
)
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛线物与x轴的交点为(-1,0),(3,0)
7.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,已知AP=3,则PP′的长度是(
)
A.3
B.3
C.5
D.4
8.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是(
)
A.OC∥AE
B.EC=BC
C.∠DAE=∠ABE
D.AC⊥OD
9.正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为(
)
A.
B.
C.
D.
第9题图 第10题图
10.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数为(
)
A.1
B.2
C.3
D.4
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知函数y=-x2+2x+c的图象经过点(1,-2),则c=
.
12.某小区2017年屋顶绿化面积为2
000平方米,计划2
019年屋顶绿化面积要达到2
880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是
%.
13.若从-1,1,2这三个数中,任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是
.
14.某广场中心有高低不同的各种喷泉,其中一支高度为米的喷水管喷水最大高度为4米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数解析式是
第14题图第15题图 第16题图
15.如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上.将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′,B′C′与CD相交于点M,则点M的坐标为
.
16.如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以点O为圆心,以OA长为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是
.
17.若α,β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为
.
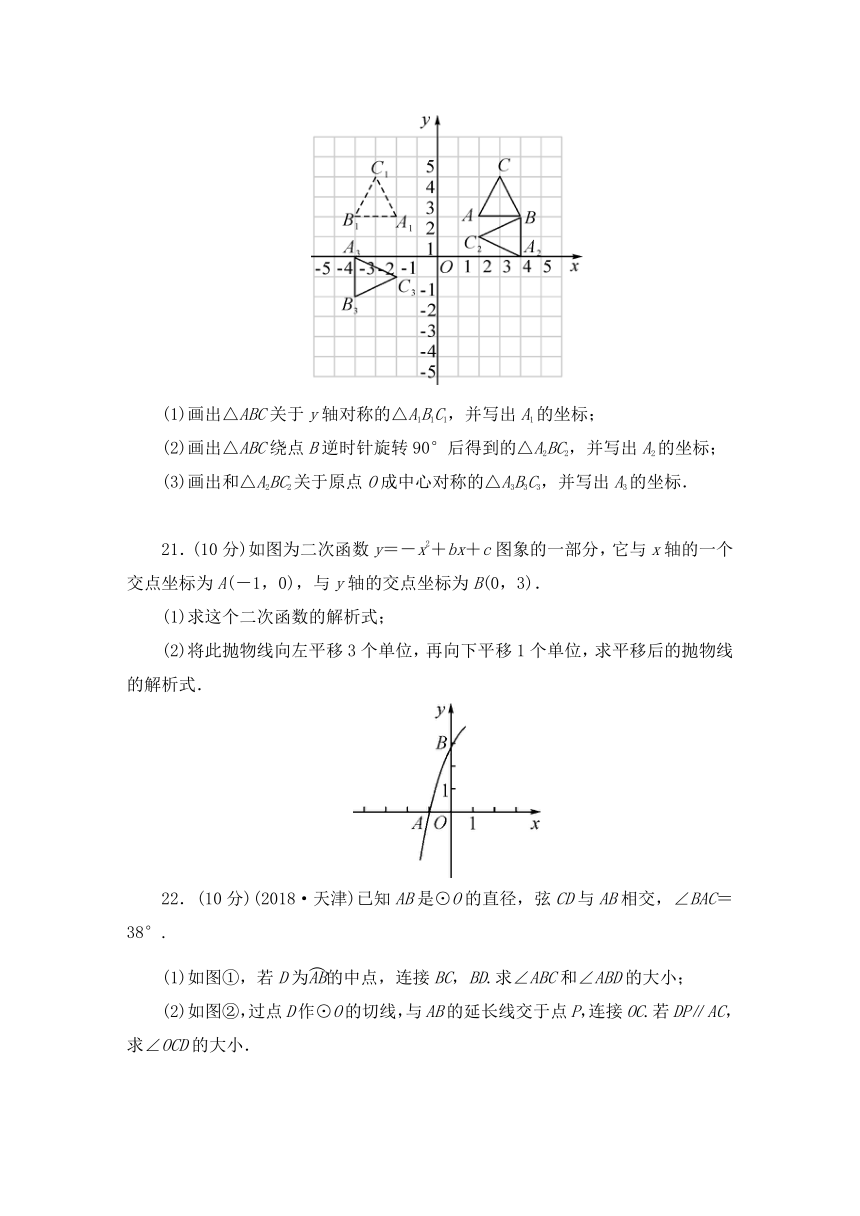
18.如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为
三、解答题(本大题共7小题,共66分)
19.(6分)解方程:
(1)x2-4x-8=0;
(2)3x-6=x(x-2).
20.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2),请解答下列问题;
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标;
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2BC2,并写出A2的坐标;
(3)画出和△A2BC2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
21.(10分)如图为二次函数y=-x2+bx+c图象的一部分,它与x轴的一个交点坐标为A(-1,0),与y轴的交点坐标为B(0,3).
(1)求这个二次函数的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
22.(10分)(2018·天津)已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为的中点,连接BC,BD.求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,连接OC.若DP∥AC,求∠OCD的大小.
23.(10分)(2018·贵阳)图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点C处的概率是
;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
24.(10分)(2018·盘锦)鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反映:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3
910元的利润?
②若该店每星期想要获得不低于3
910元的利润,则每星期至少要销售该款童装多少件?
25.(12分)如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大.求出此时P点坐标和△PBC的最大面积.
答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.方程(x+1)(x-2)=x+1的解是(
D
)
A.2
B.3
C.-1,2
D.-1,3
2.在单词NAME的四个字母中,是中心对称图形的是(
A
)
A.N
B.A
C.M
D.E
3.(2018·宜昌)如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为(
D
)
A.30°
B.35°
C.40°
D.45°
第3题图 第7题图
第8题图
4.将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为(
A
)
A.y=(x-1)2+3
B.y=(x+1)2+3
C.y=(x-1)2-3
D.y=(x+1)2-3
5.(通辽中考)关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是(
A
)
6.若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是(
C
)
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛线物与x轴的交点为(-1,0),(3,0)
7.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,已知AP=3,则PP′的长度是(
B
)
A.3
B.3
C.5
D.4
8.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是(
D
)
A.OC∥AE
B.EC=BC
C.∠DAE=∠ABE
D.AC⊥OD
9.(2018·随州)正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为(
A
)
A.
B.
C.
D.
第9题图 第10题图
10.(2018·衡阳)如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数为(
D
)
A.1
B.2
C.3
D.4
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知函数y=-x2+2x+c的图象经过点(1,-2),则c=
-3
.
12.某小区2017年屋顶绿化面积为2
000平方米,计划2
019年屋顶绿化面积要达到2
880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是
20
%.
13.(2018·滨州)若从-1,1,2这三个数中,任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是
.
14.某广场中心有高低不同的各种喷泉,其中一支高度为米的喷水管喷水最大高度为4米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数解析式是y=-10+4.
第14题图第15题图 第16题图
15.(2018·潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上.将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′,B′C′与CD相交于点M,则点M的坐标为.
16.(2018·青岛)如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以点O为圆心,以OA长为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是-π.
17.若α,β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为
12
.
18.如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为
(0,0)或或
.
三、解答题(本大题共7小题,共66分)
19.(6分)解方程:
(1)x2-4x-8=0;
解:x2-4x+4=4+8,
(x-2)2=12,
∴x-2=±2,
∴x1=2+2,x2=2-2.
(2)3x-6=x(x-2).
解:3(x-2)=x(x-2),
∴(x-2)(x-3)=0,
∴x-2=0或x-3=0,
∴x1=2,x2=3.
20.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2),请解答下列问题;
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标;
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2BC2,并写出A2的坐标;
(3)画出和△A2BC2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
解:(1)画出△A1B1C1如图,A1(-2,2).
(2)画出△A2BC2如图,A2(4,0).
(3)画出△A3B3C3如图,A3(-4,0).
21.(10分)如图为二次函数y=-x2+bx+c图象的一部分,它与x轴的一个交点坐标为A(-1,0),与y轴的交点坐标为B(0,3).
(1)求这个二次函数的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
解:(1)∵二次函数经过A(-1,0),B(0,3)两点,
∴解得
∴二次函数的解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3可化为y=-(x-1)2+4,
∴抛物线y=-x2+2x+3的顶点坐标为(1,4).
又∵此抛物线向左平移3个单位,再向下平移1个单位,
∴平移后的抛物线的顶点坐标为(-2,3).
∴平移后的抛物线的解析式为y=-(x+2)2+3=-x2-4x-1.
22.(10分)(2018·天津)已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为的中点,连接BC,BD.求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,连接OC.若DP∥AC,求∠OCD的大小.
解:(1)∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°.又∵∠BAC=38°,∴∠ABC=90°-38°=52°.由D为的中点,得=,∴∠ABD=∠BCD=∠ACB=45°.
(2)如图,连接OD.
∵DP切⊙O于点D,∴OD⊥DP,即∠ODP=90°.由DP∥AC,又∠BAC=38°,∴∠P=∠BAC=38°.∵∠AOD是△ODP的外角,∴∠AOD=∠ODP+∠P=128°,∴∠ACD=∠AOD=64°.又OA=OC,得∠ACO=∠A=38°.
∴∠OCD=∠ACD-∠ACO=64°-38°=26°.
23.(10分)(2018·贵阳)图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点C处的概率是
;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
解:列表得
(a,b)
9
8
7
6
9
(9,9)
(8,9)
(7,9)
(6,9)
8
(9,8)
(8,8)
(7,8)
(6,8)
7
(9,7)
(8,7)
(7,7)
(6,7)
6
(9,6)
(8,6)
(7,6)
(6,6)
共有16种等可能结果,和为14可以到达点C,有3种结果,所以棋子最终跳动到点C处的概率为.
24.(10分)(2018·盘锦)鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反映:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3
910元的利润?
②若该店每星期想要获得不低于3
910元的利润,则每星期至少要销售该款童装多少件?
解:(1)y=100+10(60-x)=-10x+700.
(2)设每星期的销售利润为W元,
W=(x-30)(-10x+700)=-10(x-50)2+4
000.
∴当x=50时,W最大=4
000.
∴每件售价定为50元时,每星期的销售利润最大,最大利润为4
000元.
(3)①由题意得-10(x-50)2+4
000=3
910,
解得x=53或47,∴当每件童装售价定为53元或47元时,该店一星期可获得3
910元的利润.
②由(1)知抛物线y=-10(x-50)2+4
000过点(53,3
910),(47,3
910),当y>3
910时,x的取值范围为47≤x≤53,
∵y=-10x+700.∴170≤y≤230,∴每星期至少要销售该款童装170件.
25.(12分)如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大.求出此时P点坐标和△PBC的最大面积.
解:(1)由于抛物线与x轴交于
点A(-1,0),B(4,0),可设抛物线解析式为y=a(x+1)(x-4),
将点C(0,-4)代入得a(0+1)(0-4)=-4.
解得a=1,
所求抛物线解析式为y=(x+1)(x-4),
即y=x2-3x-4.
(2)存在.
如解图①,取OC的中点D(0,-2),过D作PD⊥y轴,交抛物线点P,且点P在第四象限,则点P的纵坐标为-2,
∴x2-3x-4=-2,解得x=(负值舍去),
满足条件的P点的坐标为;
(3)∵点B(4,0),点C(0,-4),
∴直线BC的解析式为y=x-4,
设点P的坐标为(t,t2-3t-4),
如解图②,过P作PQ∥y轴交BC于Q,则点Q的坐标为(t,t-4),
∴|PQ|=t-4-(t2-3t-4)=-t2+4t=
-(t-2)2+4,
∴当t=2时,PQ取最大值,最大值为4,
∵S△PBC=S△PCQ+S△PBQ=PQ·xB=PQ·4=2PQ,
∴当PQ最大时,S△PBC最大,最大值为8.
此时点P的坐标为(2,-6).
一、选择题(本大题共10小题,每小题3分,共30分)
1.方程(x+1)(x-2)=x+1的解是(
)
A.2
B.3
C.-1,2
D.-1,3
2.在单词NAME的四个字母中,是中心对称图形的是(
)
A.N
B.A
C.M
D.E
3.(2018·宜昌)如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为(
)
A.30°
B.35°
C.40°
D.45°
第3题图 第7题图
第8题图
4.将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为(
)
A.y=(x-1)2+3
B.y=(x+1)2+3
C.y=(x-1)2-3
D.y=(x+1)2-3
5.关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是(
)
6.若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是(
)
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛线物与x轴的交点为(-1,0),(3,0)
7.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,已知AP=3,则PP′的长度是(
)
A.3
B.3
C.5
D.4
8.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是(
)
A.OC∥AE
B.EC=BC
C.∠DAE=∠ABE
D.AC⊥OD
9.正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为(
)
A.
B.
C.
D.
第9题图 第10题图
10.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数为(
)
A.1
B.2
C.3
D.4
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知函数y=-x2+2x+c的图象经过点(1,-2),则c=
.
12.某小区2017年屋顶绿化面积为2
000平方米,计划2
019年屋顶绿化面积要达到2
880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是
%.
13.若从-1,1,2这三个数中,任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是
.
14.某广场中心有高低不同的各种喷泉,其中一支高度为米的喷水管喷水最大高度为4米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数解析式是
第14题图第15题图 第16题图
15.如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上.将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′,B′C′与CD相交于点M,则点M的坐标为
.
16.如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以点O为圆心,以OA长为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是
.
17.若α,β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为
.
18.如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为
三、解答题(本大题共7小题,共66分)
19.(6分)解方程:
(1)x2-4x-8=0;
(2)3x-6=x(x-2).
20.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2),请解答下列问题;
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标;
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2BC2,并写出A2的坐标;
(3)画出和△A2BC2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
21.(10分)如图为二次函数y=-x2+bx+c图象的一部分,它与x轴的一个交点坐标为A(-1,0),与y轴的交点坐标为B(0,3).
(1)求这个二次函数的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
22.(10分)(2018·天津)已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为的中点,连接BC,BD.求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,连接OC.若DP∥AC,求∠OCD的大小.
23.(10分)(2018·贵阳)图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点C处的概率是
;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
24.(10分)(2018·盘锦)鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反映:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3
910元的利润?
②若该店每星期想要获得不低于3
910元的利润,则每星期至少要销售该款童装多少件?
25.(12分)如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大.求出此时P点坐标和△PBC的最大面积.
答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.方程(x+1)(x-2)=x+1的解是(
D
)
A.2
B.3
C.-1,2
D.-1,3
2.在单词NAME的四个字母中,是中心对称图形的是(
A
)
A.N
B.A
C.M
D.E
3.(2018·宜昌)如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为(
D
)
A.30°
B.35°
C.40°
D.45°
第3题图 第7题图
第8题图
4.将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为(
A
)
A.y=(x-1)2+3
B.y=(x+1)2+3
C.y=(x-1)2-3
D.y=(x+1)2-3
5.(通辽中考)关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是(
A
)
6.若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是(
C
)
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛线物与x轴的交点为(-1,0),(3,0)
7.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,已知AP=3,则PP′的长度是(
B
)
A.3
B.3
C.5
D.4
8.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是(
D
)
A.OC∥AE
B.EC=BC
C.∠DAE=∠ABE
D.AC⊥OD
9.(2018·随州)正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为(
A
)
A.
B.
C.
D.
第9题图 第10题图
10.(2018·衡阳)如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数为(
D
)
A.1
B.2
C.3
D.4
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知函数y=-x2+2x+c的图象经过点(1,-2),则c=
-3
.
12.某小区2017年屋顶绿化面积为2
000平方米,计划2
019年屋顶绿化面积要达到2
880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是
20
%.
13.(2018·滨州)若从-1,1,2这三个数中,任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是
.
14.某广场中心有高低不同的各种喷泉,其中一支高度为米的喷水管喷水最大高度为4米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数解析式是y=-10+4.
第14题图第15题图 第16题图
15.(2018·潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上.将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′,B′C′与CD相交于点M,则点M的坐标为.
16.(2018·青岛)如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以点O为圆心,以OA长为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是-π.
17.若α,β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为
12
.
18.如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为
(0,0)或或
.
三、解答题(本大题共7小题,共66分)
19.(6分)解方程:
(1)x2-4x-8=0;
解:x2-4x+4=4+8,
(x-2)2=12,
∴x-2=±2,
∴x1=2+2,x2=2-2.
(2)3x-6=x(x-2).
解:3(x-2)=x(x-2),
∴(x-2)(x-3)=0,
∴x-2=0或x-3=0,
∴x1=2,x2=3.
20.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2),请解答下列问题;
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标;
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2BC2,并写出A2的坐标;
(3)画出和△A2BC2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
解:(1)画出△A1B1C1如图,A1(-2,2).
(2)画出△A2BC2如图,A2(4,0).
(3)画出△A3B3C3如图,A3(-4,0).
21.(10分)如图为二次函数y=-x2+bx+c图象的一部分,它与x轴的一个交点坐标为A(-1,0),与y轴的交点坐标为B(0,3).
(1)求这个二次函数的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
解:(1)∵二次函数经过A(-1,0),B(0,3)两点,
∴解得
∴二次函数的解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3可化为y=-(x-1)2+4,
∴抛物线y=-x2+2x+3的顶点坐标为(1,4).
又∵此抛物线向左平移3个单位,再向下平移1个单位,
∴平移后的抛物线的顶点坐标为(-2,3).
∴平移后的抛物线的解析式为y=-(x+2)2+3=-x2-4x-1.
22.(10分)(2018·天津)已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为的中点,连接BC,BD.求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,连接OC.若DP∥AC,求∠OCD的大小.
解:(1)∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°.又∵∠BAC=38°,∴∠ABC=90°-38°=52°.由D为的中点,得=,∴∠ABD=∠BCD=∠ACB=45°.
(2)如图,连接OD.
∵DP切⊙O于点D,∴OD⊥DP,即∠ODP=90°.由DP∥AC,又∠BAC=38°,∴∠P=∠BAC=38°.∵∠AOD是△ODP的外角,∴∠AOD=∠ODP+∠P=128°,∴∠ACD=∠AOD=64°.又OA=OC,得∠ACO=∠A=38°.
∴∠OCD=∠ACD-∠ACO=64°-38°=26°.
23.(10分)(2018·贵阳)图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点C处的概率是
;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
解:列表得
(a,b)
9
8
7
6
9
(9,9)
(8,9)
(7,9)
(6,9)
8
(9,8)
(8,8)
(7,8)
(6,8)
7
(9,7)
(8,7)
(7,7)
(6,7)
6
(9,6)
(8,6)
(7,6)
(6,6)
共有16种等可能结果,和为14可以到达点C,有3种结果,所以棋子最终跳动到点C处的概率为.
24.(10分)(2018·盘锦)鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反映:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3
910元的利润?
②若该店每星期想要获得不低于3
910元的利润,则每星期至少要销售该款童装多少件?
解:(1)y=100+10(60-x)=-10x+700.
(2)设每星期的销售利润为W元,
W=(x-30)(-10x+700)=-10(x-50)2+4
000.
∴当x=50时,W最大=4
000.
∴每件售价定为50元时,每星期的销售利润最大,最大利润为4
000元.
(3)①由题意得-10(x-50)2+4
000=3
910,
解得x=53或47,∴当每件童装售价定为53元或47元时,该店一星期可获得3
910元的利润.
②由(1)知抛物线y=-10(x-50)2+4
000过点(53,3
910),(47,3
910),当y>3
910时,x的取值范围为47≤x≤53,
∵y=-10x+700.∴170≤y≤230,∴每星期至少要销售该款童装170件.
25.(12分)如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大.求出此时P点坐标和△PBC的最大面积.
解:(1)由于抛物线与x轴交于
点A(-1,0),B(4,0),可设抛物线解析式为y=a(x+1)(x-4),
将点C(0,-4)代入得a(0+1)(0-4)=-4.
解得a=1,
所求抛物线解析式为y=(x+1)(x-4),
即y=x2-3x-4.
(2)存在.
如解图①,取OC的中点D(0,-2),过D作PD⊥y轴,交抛物线点P,且点P在第四象限,则点P的纵坐标为-2,
∴x2-3x-4=-2,解得x=(负值舍去),
满足条件的P点的坐标为;
(3)∵点B(4,0),点C(0,-4),
∴直线BC的解析式为y=x-4,
设点P的坐标为(t,t2-3t-4),
如解图②,过P作PQ∥y轴交BC于Q,则点Q的坐标为(t,t-4),
∴|PQ|=t-4-(t2-3t-4)=-t2+4t=
-(t-2)2+4,
∴当t=2时,PQ取最大值,最大值为4,
∵S△PBC=S△PCQ+S△PBQ=PQ·xB=PQ·4=2PQ,
∴当PQ最大时,S△PBC最大,最大值为8.
此时点P的坐标为(2,-6).
同课章节目录
