2020-2021学年人教版八年级下册数学 17.1勾股定理 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 17.1勾股定理 同步练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 11:11:01 | ||
图片预览



文档简介
17.1勾股定理 同步练习
一.选择题
1.在Rt△ABC中,∠C=90°,已知a:b=3:4,c=10,其中a,b,c分别为∠A,∠B,∠C的对边,则a的长为( )
A.3 B.6 C.8 D.12
2.Rt△一直角边的长为11,另两边为自然数,则Rt△的周长为( )
A.121 B.120 C.132 D.不能确定
3.在△ABC中,若∠A:∠B:∠C=1:2:3,则a:b:c=( )
A.1:2:3 B.1:2: C.1::2 D.:1:2
4.以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则S1,S2,S3之间的关系是( )
A.S1+S2>S3 B.S1+S2<S3
C.S1+S2=S3 D.S12+S22=S32
5.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB,则CD等于( )
A.4.8 B.14 C.10 D.2.4
6.如图所示,在△ABC中,∠ABC=90°,分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
A.175 B.600 C.25 D.625
7.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.AB= B.∠BAC=90°
C.S△ABC=10 D.点A到直线BC的距离是2
8.如图数轴上的点O表示的数是0,点A表示的数是2,OB⊥OA,垂足为O,且OB=1,以A为圆心,AB长为半径画弧,交数轴于点C,则点C表示的数为( )
A.﹣ B.﹣2+ C.2﹣ D.﹣2﹣
9.如图,已知在△ABC中,∠C=90°,D为AC一点,AB=,BD=3,AD=1,则CD的长为( )
A. B. C. D.
10.如图在四边形ABCD中,对角线AC,BD交于点E,∠BDA=90°,∠CBE=30°,∠CEB=45°,AE=4EC,BC=4,则CD的长为( )
A.6 B.2 C.2 D.6
二.填空题
11.如果一个直角三角形的两条直角边的长分别是5和12,那么这个直角三角形斜边长是 .
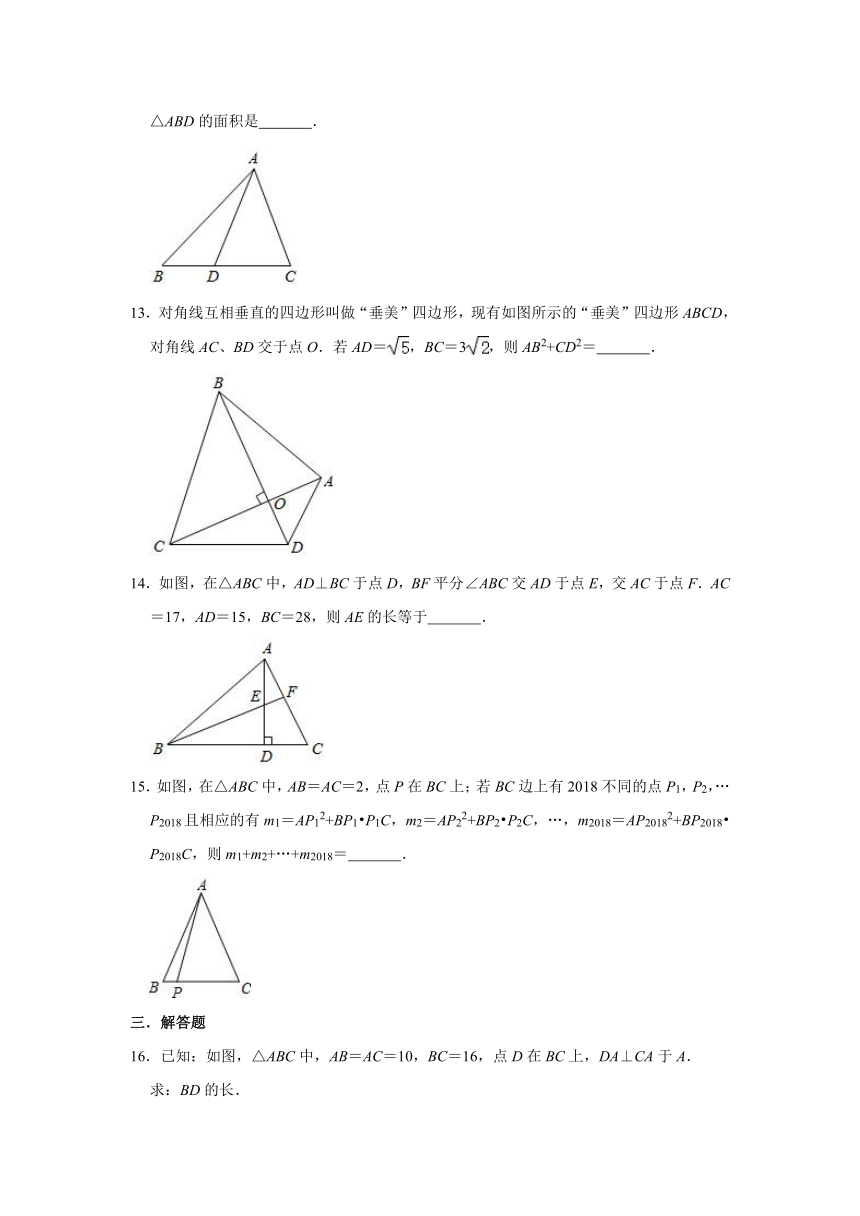
12.如图,在△ABC中,点D边BC上一点,∠DAC=∠B=45°,AB=6,BC=,则△ABD的面积是 .
13.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=,BC=3,则AB2+CD2= .
14.如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.AC=17,AD=15,BC=28,则AE的长等于 .
15.如图,在△ABC中,AB=AC=2,点P在BC上;若BC边上有2018不同的点P1,P2,…P2018且相应的有m1=AP12+BP1?P1C,m2=AP22+BP2?P2C,…,m2018=AP20182+BP2018?P2018C,则m1+m2+…+m2018= .
三.解答题
16.已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
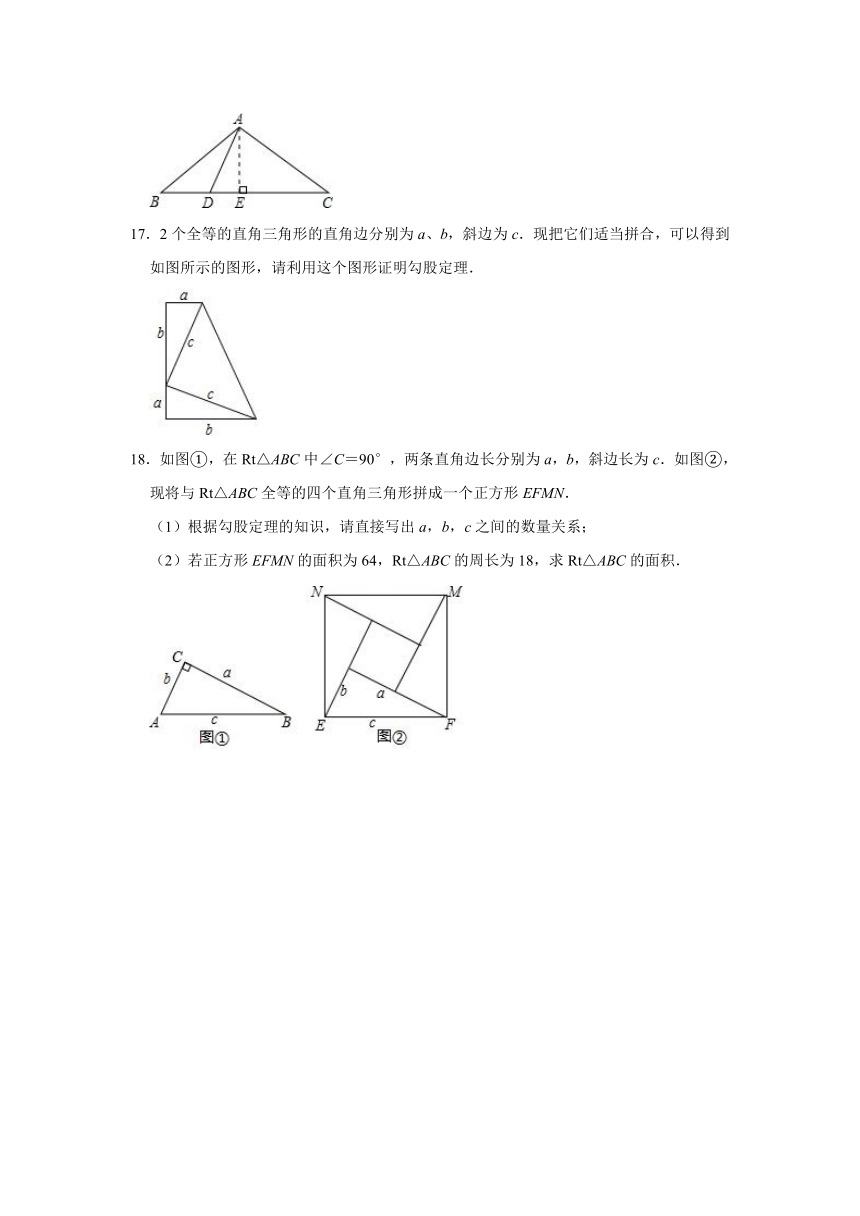
17.2个全等的直角三角形的直角边分别为a、b,斜边为c.现把它们适当拼合,可以得到如图所示的图形,请利用这个图形证明勾股定理.
18.如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
参考答案
一.选择题
1.解:由a:b=3:4,设a=3k,b=4k,
在Rt△ABC中,a=3k,b=4k,c=10,
根据勾股定理得:a2+b2=c2,即9k2+16k2=100,
解得:k=2或k=﹣2(舍去),
则a=3k=6.
故选:B.
2.解:设另一直角边为x,斜边为y.
根据勾股定理得:
y2=x2+121,即y2﹣x2=121,
(y+x)(y﹣x)=121=121×1,
∵x,y为自然数,
∴x+y=121,y﹣x=1,
∴x=60,y=61,
∴周长为:11+61+60=132.
故选:C.
3.解:∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°.
设a=k,则c=2k,
根据勾股定理,得
b=k.
则a:b:c=1::2.
故选:C.
4.解:设直角三角形三边分别为a,b,c,则a2+b2=c2
以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则分别是,,,
∴它们之间的关系为S1+S2=S3
故选:C.
5.解:∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∴AC?BC=AB?CD,即6×8=10×CD,
解得,CD=4.8,
故选:A.
6.解:由勾股定理得,AB2+BC2=AC2,
则S=25+400=625,
故选:D.
7.解:由题意可得,
AB==2,故选项A正确;
AC==,
BC==5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,故选项B正确;
∴S△ABC==5,故选项C错误;
作AD⊥BC于点D,
则=5,
即=5,
解得,AD=2,
即点A到直线BC的距离是2,故选项D正确;
故选:C.
8.解:在Rt△AOB中,AB===,
∴AB=AC=,
∴OC=AC﹣OA=﹣2,
∵C点在x轴负半轴,
∴点C表示的数为2﹣.
故选:C.
9.解:设CD=x,则AC=x+1,
∵∠C=90°,
∴BC2=BD2﹣CD2=AB2﹣AC2,
∴32﹣x2=13﹣(x+1)2,
∴x=,
∴CD=,
故选:D.
10.解:如图,过点C作CH⊥BD于点H.
∵∠CBE=30°,BC=4,
∴CH=BC=2,
又∵∠CEB=45°,
∴EH=CH=2,则CE=2,
∵AE=4EC=8.
在直角△ADE中,∠EDA=90°,∠AED=∠CEB=45°,则AD=DE=AE=8,
∴DH=DE+EH=10,
在直角△DCH中,根据勾股定理得到CD===2.
故选:B.
二.填空题
11.解:∵两条直角边的长分别是5和12,
∴斜边=,
故答案为:13.
12.解:如图,过点A作EA⊥AB交BC的延长线于E,过点C作CF⊥AE于点F,过点A作AG⊥BC于G,
∵∠B=45°,
∴∠E=90°﹣45°=45°,
∴AE=AB=6,
由勾股定理得BE==6,
∴AG=3,CE=BE﹣BC=2,
∵EF⊥AE,∠E=45°,
∴△CFE为等腰直角三角形,
∴CF=FE=CE=2,
∴AF=AE﹣EF=4,
在Rt△ACF中,
AC==2,
∵∠DAC=∠B=45°,∠ACB=∠ACB,
∴△ACB∽△DCA,
∴=,
∴=,
∴DC=,
∴BD=BC﹣DC=,
∴△ABD的面积=×BD×AG=××3=.
故答案为:.
13.解:∵AC⊥BD,
∴∠BOC=∠COD=∠DOA=∠AOB=90°,
∴OB2+OC2=BC2,OA2+OD2=AD2,OB2+OA2=AB2,OC2+OD2=CD2,
∴AB2+CD2=OB2+OA2+OC2+OD2=BC2+AD2,
∵AD=,BC=3,
∴BC2+AD2=(3)2+()2=18+5=23,
∴AB2+CD2=23,
故答案为:23.
14.解:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵AD=15,AC=17,
∴DC=,
∵BC=28,
∴BD=28﹣8=20,
由勾股定理得:AB=,
过点E作EG⊥AB于G,
∵BF平分∠ABC,AD⊥BC,
∴EG=ED,
在Rt△BDE和Rt△BGE中,
∵,
∴Rt△BDE≌Rt△BGE(HL),
∴BG=BD=20,
∴AG=25﹣20=5,
设AE=x,则ED=15﹣x,
∴EG=15﹣x,
Rt△AGE中,x2=52+(15﹣x)2,
x=,
∴AE=.
故答案为:.
15.解:如图所示:
过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD.
在Rt△ABD中,AB2=AD2+BD2①,
在Rt△APD中,AP12=AD2+P1D2②,
①﹣②得:AB2﹣AP12=BD2﹣P1D2=(BD+P1D)(BD﹣P1D)=P1C?BP1,
∴m1=AB2=AP12+BP1?P1C=4,
同理:m2=AB2=AP22+BP2?P2C=4,
m3=AB2=AP32+BP3?P3C,
…
m1+m2+…+m2018=4×2018=8072,
故答案为:8072.
三.解答题
16.解:过点A作AE⊥BC于点E,
∵AB=AC=10,BC=16,
∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE===6,
设BD=x,则DE=8﹣x,DC=16﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,
代入为:62+(8﹣x)2=(16﹣x)2﹣102,解得:x=.
即BD=.
17.证明:∵四边形ABCD是梯形,
∴梯形的面积=(a+b)(a+b)=2××ab+c2,
即(a2+2ab+b2)=ab+c2,
∴a2+b2=c2.
18.解:(1)由勾股定理得,a2+b2=c2;
(2)∵正方形EFMN的面积为64,
∴c2=64,即c=8,
∵Rt△ABC的周长为18,
∴a+b+c=18,
∴a+b=10,
则Rt△ABC的面积=ab
=[(a+b)2﹣(a2+b2)]
=9.
一.选择题
1.在Rt△ABC中,∠C=90°,已知a:b=3:4,c=10,其中a,b,c分别为∠A,∠B,∠C的对边,则a的长为( )
A.3 B.6 C.8 D.12
2.Rt△一直角边的长为11,另两边为自然数,则Rt△的周长为( )
A.121 B.120 C.132 D.不能确定
3.在△ABC中,若∠A:∠B:∠C=1:2:3,则a:b:c=( )
A.1:2:3 B.1:2: C.1::2 D.:1:2
4.以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则S1,S2,S3之间的关系是( )
A.S1+S2>S3 B.S1+S2<S3
C.S1+S2=S3 D.S12+S22=S32
5.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB,则CD等于( )
A.4.8 B.14 C.10 D.2.4
6.如图所示,在△ABC中,∠ABC=90°,分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
A.175 B.600 C.25 D.625
7.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.AB= B.∠BAC=90°
C.S△ABC=10 D.点A到直线BC的距离是2
8.如图数轴上的点O表示的数是0,点A表示的数是2,OB⊥OA,垂足为O,且OB=1,以A为圆心,AB长为半径画弧,交数轴于点C,则点C表示的数为( )
A.﹣ B.﹣2+ C.2﹣ D.﹣2﹣
9.如图,已知在△ABC中,∠C=90°,D为AC一点,AB=,BD=3,AD=1,则CD的长为( )
A. B. C. D.
10.如图在四边形ABCD中,对角线AC,BD交于点E,∠BDA=90°,∠CBE=30°,∠CEB=45°,AE=4EC,BC=4,则CD的长为( )
A.6 B.2 C.2 D.6
二.填空题
11.如果一个直角三角形的两条直角边的长分别是5和12,那么这个直角三角形斜边长是 .
12.如图,在△ABC中,点D边BC上一点,∠DAC=∠B=45°,AB=6,BC=,则△ABD的面积是 .
13.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=,BC=3,则AB2+CD2= .
14.如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.AC=17,AD=15,BC=28,则AE的长等于 .
15.如图,在△ABC中,AB=AC=2,点P在BC上;若BC边上有2018不同的点P1,P2,…P2018且相应的有m1=AP12+BP1?P1C,m2=AP22+BP2?P2C,…,m2018=AP20182+BP2018?P2018C,则m1+m2+…+m2018= .
三.解答题
16.已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
17.2个全等的直角三角形的直角边分别为a、b,斜边为c.现把它们适当拼合,可以得到如图所示的图形,请利用这个图形证明勾股定理.
18.如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
参考答案
一.选择题
1.解:由a:b=3:4,设a=3k,b=4k,
在Rt△ABC中,a=3k,b=4k,c=10,
根据勾股定理得:a2+b2=c2,即9k2+16k2=100,
解得:k=2或k=﹣2(舍去),
则a=3k=6.
故选:B.
2.解:设另一直角边为x,斜边为y.
根据勾股定理得:
y2=x2+121,即y2﹣x2=121,
(y+x)(y﹣x)=121=121×1,
∵x,y为自然数,
∴x+y=121,y﹣x=1,
∴x=60,y=61,
∴周长为:11+61+60=132.
故选:C.
3.解:∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°.
设a=k,则c=2k,
根据勾股定理,得
b=k.
则a:b:c=1::2.
故选:C.
4.解:设直角三角形三边分别为a,b,c,则a2+b2=c2
以一直角三角形三边为直径所作的半圆面积,由小到大依次为S1,S2,S3,则分别是,,,
∴它们之间的关系为S1+S2=S3
故选:C.
5.解:∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∴AC?BC=AB?CD,即6×8=10×CD,
解得,CD=4.8,
故选:A.
6.解:由勾股定理得,AB2+BC2=AC2,
则S=25+400=625,
故选:D.
7.解:由题意可得,
AB==2,故选项A正确;
AC==,
BC==5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,故选项B正确;
∴S△ABC==5,故选项C错误;
作AD⊥BC于点D,
则=5,
即=5,
解得,AD=2,
即点A到直线BC的距离是2,故选项D正确;
故选:C.
8.解:在Rt△AOB中,AB===,
∴AB=AC=,
∴OC=AC﹣OA=﹣2,
∵C点在x轴负半轴,
∴点C表示的数为2﹣.
故选:C.
9.解:设CD=x,则AC=x+1,
∵∠C=90°,
∴BC2=BD2﹣CD2=AB2﹣AC2,
∴32﹣x2=13﹣(x+1)2,
∴x=,
∴CD=,
故选:D.
10.解:如图,过点C作CH⊥BD于点H.
∵∠CBE=30°,BC=4,
∴CH=BC=2,
又∵∠CEB=45°,
∴EH=CH=2,则CE=2,
∵AE=4EC=8.
在直角△ADE中,∠EDA=90°,∠AED=∠CEB=45°,则AD=DE=AE=8,
∴DH=DE+EH=10,
在直角△DCH中,根据勾股定理得到CD===2.
故选:B.
二.填空题
11.解:∵两条直角边的长分别是5和12,
∴斜边=,
故答案为:13.
12.解:如图,过点A作EA⊥AB交BC的延长线于E,过点C作CF⊥AE于点F,过点A作AG⊥BC于G,
∵∠B=45°,
∴∠E=90°﹣45°=45°,
∴AE=AB=6,
由勾股定理得BE==6,
∴AG=3,CE=BE﹣BC=2,
∵EF⊥AE,∠E=45°,
∴△CFE为等腰直角三角形,
∴CF=FE=CE=2,
∴AF=AE﹣EF=4,
在Rt△ACF中,
AC==2,
∵∠DAC=∠B=45°,∠ACB=∠ACB,
∴△ACB∽△DCA,
∴=,
∴=,
∴DC=,
∴BD=BC﹣DC=,
∴△ABD的面积=×BD×AG=××3=.
故答案为:.
13.解:∵AC⊥BD,
∴∠BOC=∠COD=∠DOA=∠AOB=90°,
∴OB2+OC2=BC2,OA2+OD2=AD2,OB2+OA2=AB2,OC2+OD2=CD2,
∴AB2+CD2=OB2+OA2+OC2+OD2=BC2+AD2,
∵AD=,BC=3,
∴BC2+AD2=(3)2+()2=18+5=23,
∴AB2+CD2=23,
故答案为:23.
14.解:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵AD=15,AC=17,
∴DC=,
∵BC=28,
∴BD=28﹣8=20,
由勾股定理得:AB=,
过点E作EG⊥AB于G,
∵BF平分∠ABC,AD⊥BC,
∴EG=ED,
在Rt△BDE和Rt△BGE中,
∵,
∴Rt△BDE≌Rt△BGE(HL),
∴BG=BD=20,
∴AG=25﹣20=5,
设AE=x,则ED=15﹣x,
∴EG=15﹣x,
Rt△AGE中,x2=52+(15﹣x)2,
x=,
∴AE=.
故答案为:.
15.解:如图所示:
过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD.
在Rt△ABD中,AB2=AD2+BD2①,
在Rt△APD中,AP12=AD2+P1D2②,
①﹣②得:AB2﹣AP12=BD2﹣P1D2=(BD+P1D)(BD﹣P1D)=P1C?BP1,
∴m1=AB2=AP12+BP1?P1C=4,
同理:m2=AB2=AP22+BP2?P2C=4,
m3=AB2=AP32+BP3?P3C,
…
m1+m2+…+m2018=4×2018=8072,
故答案为:8072.
三.解答题
16.解:过点A作AE⊥BC于点E,
∵AB=AC=10,BC=16,
∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE===6,
设BD=x,则DE=8﹣x,DC=16﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,
代入为:62+(8﹣x)2=(16﹣x)2﹣102,解得:x=.
即BD=.
17.证明:∵四边形ABCD是梯形,
∴梯形的面积=(a+b)(a+b)=2××ab+c2,
即(a2+2ab+b2)=ab+c2,
∴a2+b2=c2.
18.解:(1)由勾股定理得,a2+b2=c2;
(2)∵正方形EFMN的面积为64,
∴c2=64,即c=8,
∵Rt△ABC的周长为18,
∴a+b+c=18,
∴a+b=10,
则Rt△ABC的面积=ab
=[(a+b)2﹣(a2+b2)]
=9.
