2020-2021学年七年级数学人教版 下册 5.2 平行线及其判定 同步课时训练(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学人教版 下册 5.2 平行线及其判定 同步课时训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 11:13:22 | ||
图片预览


文档简介
人教版
七年级数学下册
5.2
平行线及其判定
同步课时训练
一、选择题
1.
图是一条街道的路线图,若AB∥CD,且∠ABC=130°,则当∠CDE等于 时,BC∥DE
( )?
A.40°
B.50°
C.70°
D.130°
2.
如图,∠1=120°,要使a∥b,则∠2的大小是
( )
A.60°
B.80°
C.100°
D.120°
3.
学员在广场上练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是(
)
A.第一次向左拐,第二次向右拐
B.第一次向右拐,第二次向左拐
C.第一次向右拐,第二次向右拐
D.第一次向左拐,第二次向左拐
4.
如图,在下列给出的条件中,不能判定AB∥CD的是
()
A.∠BAD+∠ADC=180°
B.∠ABD=∠BDC
C.∠ADB=∠DBC
D.∠ABE=∠DCE
5.
如图,已知AB∥CD,下列能判定BE∥CF的条件是
( )
A.∠1=∠3
B.∠2=∠4
C.∠1=∠4
D.∠1=∠2
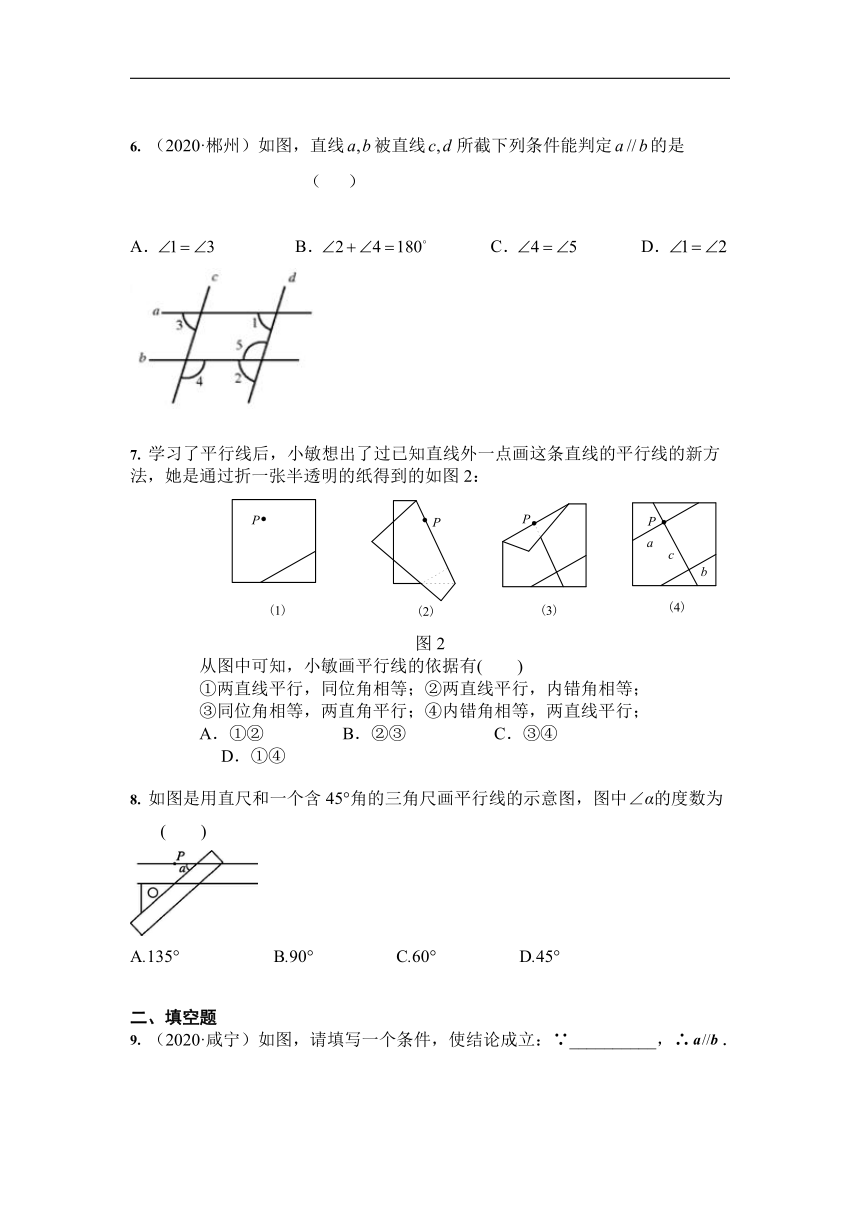
6.
(2020·郴州)如图,直线被直线所截下列条件能判定的是
(
)
A.
B.
C.
D.
7.
学行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的如图2:
图2
从图中可知,小敏画平行线的依据有(
)
①两直线平行,同位角相等;②两直线平行,内错角相等;
③同位角相等,两直角平行;④内错角相等,两直线平行;
A.①②
B.②③
C.③④
D.①④
8.
如图是用直尺和一个含45°角的三角尺画平行线的示意图,图中∠α的度数为
( )
A.135°
B.90°
C.60°
D.45°
二、填空题
9.
(2020·咸宁)如图,请填写一个条件,使结论成立:∵__________,∴.
10.
已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,那么AD是∠BAC的平分线吗?若是,请说明理由.请补全下面解答过程及依据.
解:是.理由如下:
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直的定义),
∴AD∥EG( ),?
∴∠1=∠E( ),?
∠2=∠3( ).?
∵∠E=∠3(已知),
∴ = ( ),?
∴AD是∠BAC的平分线(角平分线的定义).
11.
如图,∠1=∠2,试说明AB∥CD.
请补全以下说理过程.
解:∵∠1=∠2(已知),
且∠3=∠2(
),?
∴∠1= ( ),?
∴AB∥CD(
).?
12.
如图,如果∠BAC=∠ ,那么根据 ,?
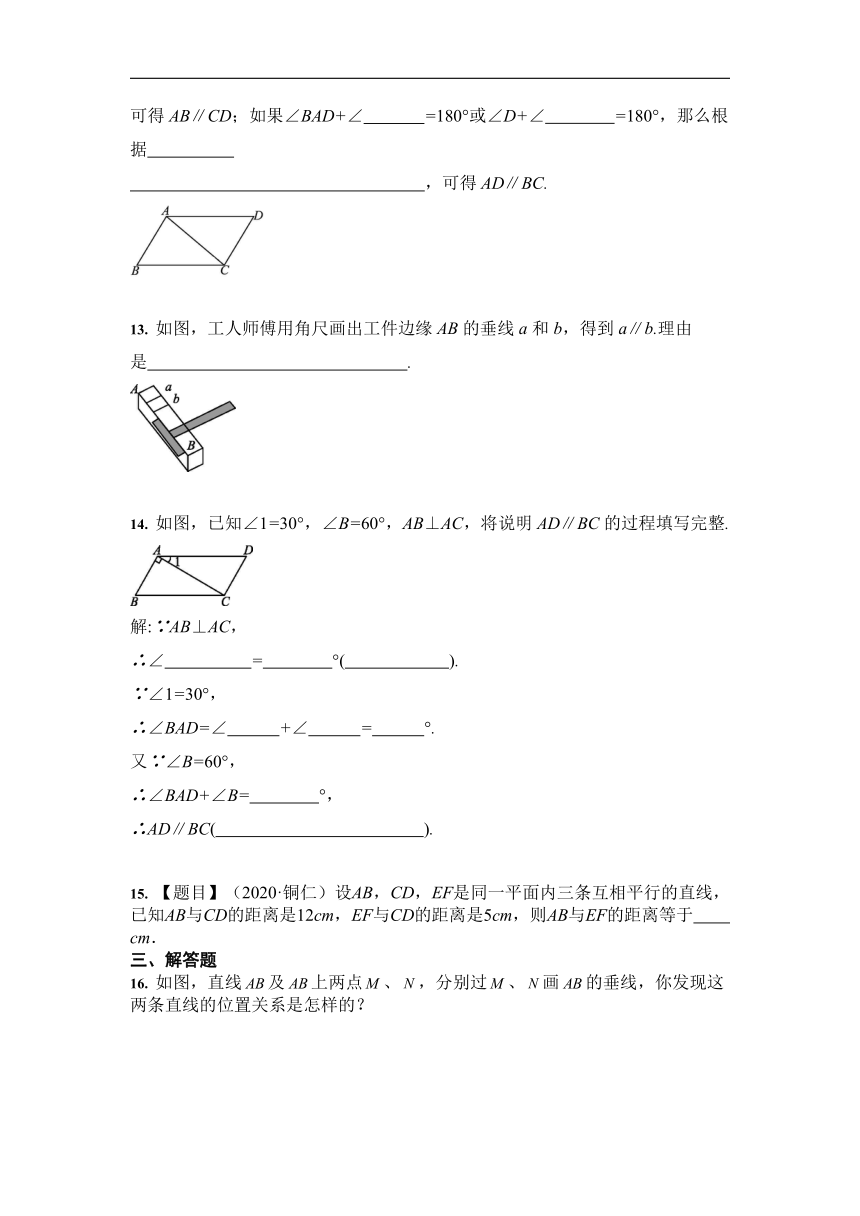
可得AB∥CD;如果∠BAD+∠
=180°或∠D+∠ =180°,那么根据
,可得AD∥BC.?
13.
如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是 .?
14.
如图,已知∠1=30°,∠B=60°,AB⊥AC,将说明AD∥BC的过程填写完整.
解:∵AB⊥AC,
∴∠ = °( ).?
∵∠1=30°,
∴∠BAD=∠ +∠ = °.?
又∵∠B=60°,
∴∠BAD+∠B= °,?
∴AD∥BC( ).?
15.
【题目】(2020·铜仁)设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于
cm.
三、解答题
16.
如图,直线及上两点、,分别过、画的垂线,你发现这两条直线的位置关系是怎样的?
17.
已知:如图,、交于点,,平分,平分,那么与平行吗?为什么?
18.
已知,如图,,试用两种方法证明
19.
我们知道,光线从空气摄入水中会发色很那个折射现象.光线从水射入空气中,同样也会发生折射现象.如图,为光线从空气射入水中,再从水射入空气中的示意图.由于折射率相同,因此有,.请你用所学的知识来判断光线与是否平行?并说明理由.
人教版
七年级数学下册
5.2
平行线及其判定
同步课时训练-答案
一、选择题
1.
【答案】B
2.
【答案】D
3.
【答案】A
【解析】选择A,注意区分拐角是与前进方向所成的角,本题考察了同位角相等,两直线平行.教师可将此题的后三个选项拓展,让学生求出两次拐角后与原方向的夹角.
4.
【答案】C
5.
【答案】C
6.
【答案】D
【解析】
A、当∠1=∠3时,c∥d,故此选项不合题意;B、当∠2+∠4=180°时,c∥d,故此选项不合题意;C、当∠4=∠5时,c∥d,故此选项不合题意;D、当∠1=∠2时,a∥b,故此选项符合题意;故选:D.
7.
【答案】由折纸方法可知,直线,都和直线互相垂直.所以,理由是③或④.故选C
8.
【答案】D
二、填空题
9.
【答案】:∠1=∠4或∠2=∠4或∠3+∠4=180°
【解析】本题考查了平行线的判定,∵∠1=∠4或∠2=∠4或∠3+∠4=180°,∴a∥b,因此本题填:∠1=∠4或∠2=∠4或∠3+∠4=180°.
10.
【答案】同位角相等,两直线平行 两直线平行,同位角相等 两直线平行,内错角相等 ∠1 ∠2 等量代换
11.
【答案】对顶角相等 ∠3 等量代换 同位角相等,两直线平行
12.
【答案】ACD 内错角相等,两直线平行 B DCB 同旁内角互补,两直线平行
13.
【答案】同位角相等,两直线平行(或同旁内角互补,两直线平行)
14.
【答案】BAC 90 垂直的定义 BAC 1 120 180
同旁内角互补,两直线平行
15.
【答案】
【解析】解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,∴EF与AB的距离为12﹣5=7(cm).
②当EF在AB,CD同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.故答案为:7或17.
三、解答题
16.
【答案】
如图,∵,,∴,
∴(同位角相等,两直线平行)
这个结论以后可以当作一个定理来用——垂直于同一直线的两直线平行.
17.
【答案】
∵(已知),∴(内错角相等,两直线平行)
∵平分,平分(已知),
∴,从而(内错角相等,两直线平行)
18.
【答案】
解法一:过点作,则,
又,
∴,
∴
解法二:作,
则,
∵,
∴,
∴,
∴,
∴
19.
【答案】
如图:
∵,,
∴(等角的补角相等)
又∵
∴
∴(内错角相等,两直线平行)
七年级数学下册
5.2
平行线及其判定
同步课时训练
一、选择题
1.
图是一条街道的路线图,若AB∥CD,且∠ABC=130°,则当∠CDE等于 时,BC∥DE
( )?
A.40°
B.50°
C.70°
D.130°
2.
如图,∠1=120°,要使a∥b,则∠2的大小是
( )
A.60°
B.80°
C.100°
D.120°
3.
学员在广场上练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是(
)
A.第一次向左拐,第二次向右拐
B.第一次向右拐,第二次向左拐
C.第一次向右拐,第二次向右拐
D.第一次向左拐,第二次向左拐
4.
如图,在下列给出的条件中,不能判定AB∥CD的是
()
A.∠BAD+∠ADC=180°
B.∠ABD=∠BDC
C.∠ADB=∠DBC
D.∠ABE=∠DCE
5.
如图,已知AB∥CD,下列能判定BE∥CF的条件是
( )
A.∠1=∠3
B.∠2=∠4
C.∠1=∠4
D.∠1=∠2
6.
(2020·郴州)如图,直线被直线所截下列条件能判定的是
(
)
A.
B.
C.
D.
7.
学行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的如图2:
图2
从图中可知,小敏画平行线的依据有(
)
①两直线平行,同位角相等;②两直线平行,内错角相等;
③同位角相等,两直角平行;④内错角相等,两直线平行;
A.①②
B.②③
C.③④
D.①④
8.
如图是用直尺和一个含45°角的三角尺画平行线的示意图,图中∠α的度数为
( )
A.135°
B.90°
C.60°
D.45°
二、填空题
9.
(2020·咸宁)如图,请填写一个条件,使结论成立:∵__________,∴.
10.
已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,那么AD是∠BAC的平分线吗?若是,请说明理由.请补全下面解答过程及依据.
解:是.理由如下:
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直的定义),
∴AD∥EG( ),?
∴∠1=∠E( ),?
∠2=∠3( ).?
∵∠E=∠3(已知),
∴ = ( ),?
∴AD是∠BAC的平分线(角平分线的定义).
11.
如图,∠1=∠2,试说明AB∥CD.
请补全以下说理过程.
解:∵∠1=∠2(已知),
且∠3=∠2(
),?
∴∠1= ( ),?
∴AB∥CD(
).?
12.
如图,如果∠BAC=∠ ,那么根据 ,?
可得AB∥CD;如果∠BAD+∠
=180°或∠D+∠ =180°,那么根据
,可得AD∥BC.?
13.
如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是 .?
14.
如图,已知∠1=30°,∠B=60°,AB⊥AC,将说明AD∥BC的过程填写完整.
解:∵AB⊥AC,
∴∠ = °( ).?
∵∠1=30°,
∴∠BAD=∠ +∠ = °.?
又∵∠B=60°,
∴∠BAD+∠B= °,?
∴AD∥BC( ).?
15.
【题目】(2020·铜仁)设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于
cm.
三、解答题
16.
如图,直线及上两点、,分别过、画的垂线,你发现这两条直线的位置关系是怎样的?
17.
已知:如图,、交于点,,平分,平分,那么与平行吗?为什么?
18.
已知,如图,,试用两种方法证明
19.
我们知道,光线从空气摄入水中会发色很那个折射现象.光线从水射入空气中,同样也会发生折射现象.如图,为光线从空气射入水中,再从水射入空气中的示意图.由于折射率相同,因此有,.请你用所学的知识来判断光线与是否平行?并说明理由.
人教版
七年级数学下册
5.2
平行线及其判定
同步课时训练-答案
一、选择题
1.
【答案】B
2.
【答案】D
3.
【答案】A
【解析】选择A,注意区分拐角是与前进方向所成的角,本题考察了同位角相等,两直线平行.教师可将此题的后三个选项拓展,让学生求出两次拐角后与原方向的夹角.
4.
【答案】C
5.
【答案】C
6.
【答案】D
【解析】
A、当∠1=∠3时,c∥d,故此选项不合题意;B、当∠2+∠4=180°时,c∥d,故此选项不合题意;C、当∠4=∠5时,c∥d,故此选项不合题意;D、当∠1=∠2时,a∥b,故此选项符合题意;故选:D.
7.
【答案】由折纸方法可知,直线,都和直线互相垂直.所以,理由是③或④.故选C
8.
【答案】D
二、填空题
9.
【答案】:∠1=∠4或∠2=∠4或∠3+∠4=180°
【解析】本题考查了平行线的判定,∵∠1=∠4或∠2=∠4或∠3+∠4=180°,∴a∥b,因此本题填:∠1=∠4或∠2=∠4或∠3+∠4=180°.
10.
【答案】同位角相等,两直线平行 两直线平行,同位角相等 两直线平行,内错角相等 ∠1 ∠2 等量代换
11.
【答案】对顶角相等 ∠3 等量代换 同位角相等,两直线平行
12.
【答案】ACD 内错角相等,两直线平行 B DCB 同旁内角互补,两直线平行
13.
【答案】同位角相等,两直线平行(或同旁内角互补,两直线平行)
14.
【答案】BAC 90 垂直的定义 BAC 1 120 180
同旁内角互补,两直线平行
15.
【答案】
【解析】解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,∴EF与AB的距离为12﹣5=7(cm).
②当EF在AB,CD同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.故答案为:7或17.
三、解答题
16.
【答案】
如图,∵,,∴,
∴(同位角相等,两直线平行)
这个结论以后可以当作一个定理来用——垂直于同一直线的两直线平行.
17.
【答案】
∵(已知),∴(内错角相等,两直线平行)
∵平分,平分(已知),
∴,从而(内错角相等,两直线平行)
18.
【答案】
解法一:过点作,则,
又,
∴,
∴
解法二:作,
则,
∵,
∴,
∴,
∴,
∴
19.
【答案】
如图:
∵,,
∴(等角的补角相等)
又∵
∴
∴(内错角相等,两直线平行)
