第一章《算法初步》1.1 算法与程序框图(提高练,含解析)—2020-2021学年人教A版必修三同步必刷题
文档属性
| 名称 | 第一章《算法初步》1.1 算法与程序框图(提高练,含解析)—2020-2021学年人教A版必修三同步必刷题 |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 23:27:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修三同步必刷题提高练
第一章《算法初步》
1.1
算法与程序框图
一.选择题
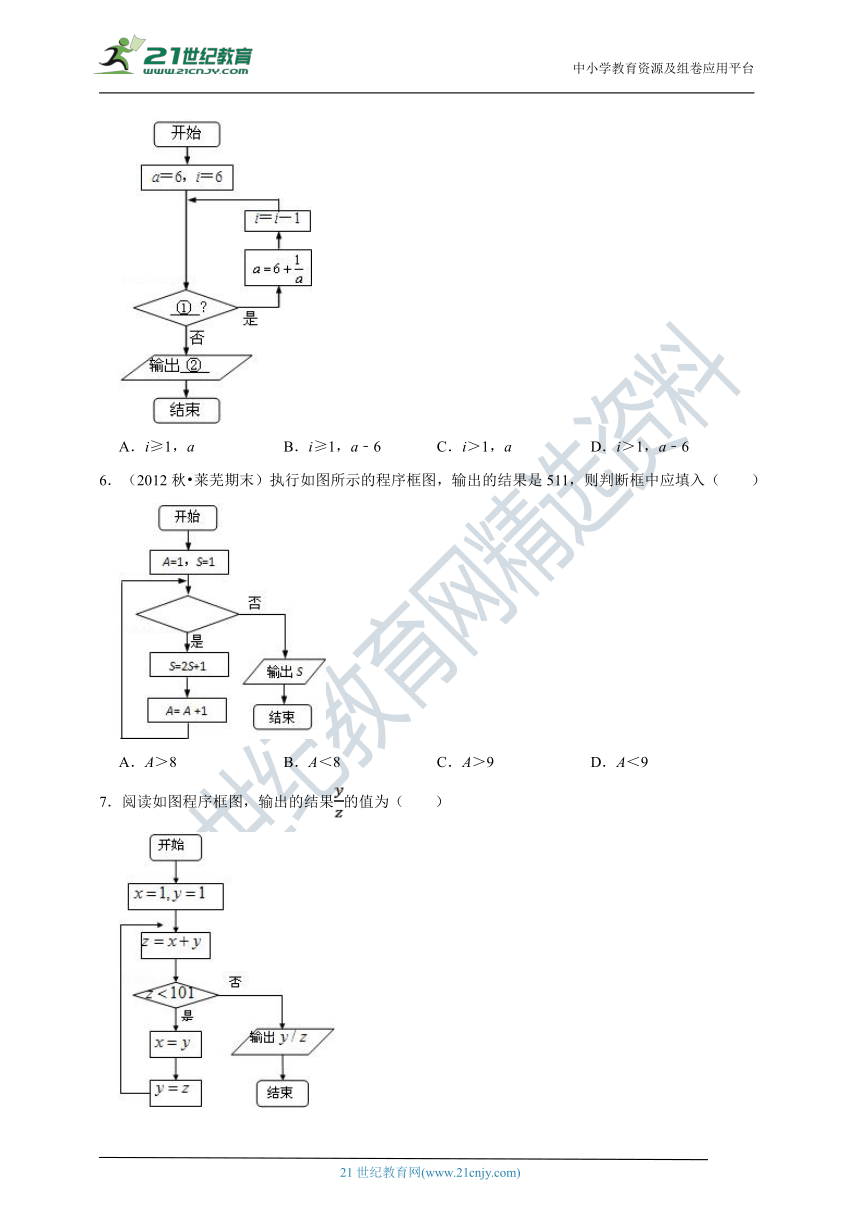
1.(2016?平果县模拟)在如图所示的程序框图中,输入A=22,B=4,则输出的结果是( )
A.0
B.2
C.4
D.6
2.(2016?甲卷模拟)对任意非零实数a,b,若a?b的运算原理如图所示,则20.5?log0.5的值为( )
A.
B.
C.
D.
3.(2015秋?三明期末)运行如图的程序后,输出的结果为( )
A.
B.
C.
D.
4.(2015秋?汉川市校级期末)如图给出的是计算1的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句分别是( )
A.n=n+2,i>5?
B.n=n+2,i=5?
C.n=n+1,i=5?
D.n=n+1,i>5?
5.(2016?河南模拟)右边程序框图的功能是求出的值,则框图中①、②两处应分别填写的是( )
A.i≥1,a
B.i≥1,a﹣6
C.i>1,a
D.i>1,a﹣6
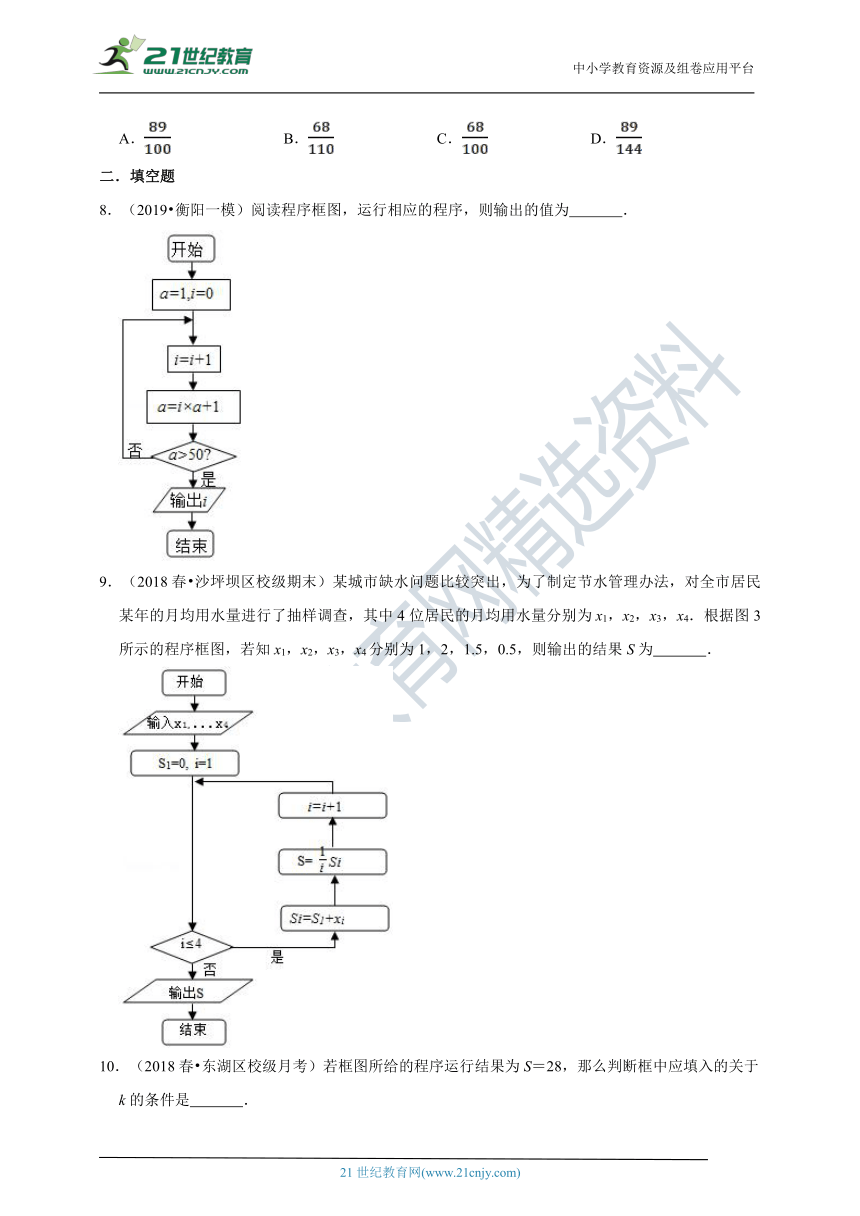
6.(2012秋?莱芜期末)执行如图所示的程序框图,输出的结果是511,则判断框中应填入( )
A.A>8
B.A<8
C.A>9
D.A<9
7.阅读如图程序框图,输出的结果的值为( )
A.
B.
C.
D.
二.填空题
8.(2019?衡阳一模)阅读程序框图,运行相应的程序,则输出的值为
.
9.(2018春?沙坪坝区校级期末)某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为x1,x2,x3,x4.根据图3所示的程序框图,若知x1,x2,x3,x4分别为1,2,1.5,0.5,则输出的结果S为
.
10.(2018春?东湖区校级月考)若框图所给的程序运行结果为S=28,那么判断框中应填入的关于k的条件是
.
11.(2018?平度市校级模拟)阅读程序框图(如图),输出的结果的值为
.
12.(2018春?陆川县校级期末)给出如图的程序框图,程序输出的结果是
.
13.(2018?河南二模)将“杨辉三角”中的数从左到右、从上到下排成一数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,如图所示程序框图用来输出此数列的前若干项并求其和,若输入m=4则相应最后的输出S的值是
.
14.(2015春?城关区校级期末)下面的程序运行后,输出的值是
15.(2015春?临沂校级月考)定义某种运算?,S=a?b的运算原理如图所示.设f(x)=(0?x)x﹣(3?x).则f(3)=
;f(x)在区间[﹣3,3]上的最小值为
.
三.解答题
16.(2013秋?清流县校级月考)在某音乐唱片超市里,每张唱片售价12元,顾客如果购买5张以上(含5张)唱片,则按照九折收费;如果购买10张以上(含10张)唱片,则按照八折收费.请将下面计费的程序框图补充完整.
17.(2016秋?晋江市校级月考)把求n!的程序补充完整.
18.(2015春?郴州校级期中)已知一个程序语句如图:
(1)若输入X的值为0,求输出Y的值?
(2)若输出Y的值为3,求输入X的值?
19.(2012秋?泰宁县校级月考)(1)辗转相除法求840与1764的最大公约数;
(2)更相减损术求153与119的最大公约数.
20.(2019春?北海期中)在如图所示的程序框图中,有这样一个执行框xi=f(xi﹣1),其中的函数关系式为f(x),程序框图中的D为函数f(x)的定义域.
(1)若输入x0,请写出输出的所有x的值;
(2)若输出的所有xi都相等,试求输入的初始值x0.
21.(2016秋?松桃县校级期中)从高二抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.
试利用频率分布直方图(图1),求(精确到小数点后一位):
(1)估算这50名学生成绩的众数;
(2)在上述统计数据的分析中有一项计算见算法流程图(图2),求输出S的值.(注:mi,fi分别是第i组分数的组中值和频率).
22.(2016春?鼓楼区期中)如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(Ⅲ)若要使输入的x的值与输出的y的值相等,则输入x的值的集合为多少?
参考答案与试题解析
一.选择题
1.【解答】解:当B=4,满足进行循环的条件,C=2,A=4,B=2,
当B=2,满足进行循环的条件,C=0,A=2,B=0,
当B=0,不满足进行循环的条件,
故输出的A值为2,
故选:B.
2.【解答】解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算分段函数y函数值,
∵20.5?log0.5?2,
此时ab=2,
∴y.
故选:C.
3.【解答】解:根据程序语言的运行过程,得
该程序运行后输出的是S;
计算S=(1)+()+()+()+()=1.
所以输出S.
故选:C.
4.【解答】解:模拟程序框图的运行过程,知;
①处表示各项的分母变化过程,
而分母相差为2,
∴n=n+2;
②处为直到型循环结构满足跳出循环体的条件,
而分母从1到9共5项,
∴i>5?.
故选:A.
5.【解答】解:程序框图是计算的值,
则利用累积加,则第一个处理框应为i>1,然后计算i是增加1个,i=i+1,
第二空输出结果a﹣6.
故选:D.
6.【解答】解:经判断此循环为“直到型“结构,判断框内为跳出循环的语句
第1次循环:S=3,A=2;第2次循环:S=7,A=3;第3次循环:S=15,A=4;第4次循环:S=31,A=5;第5次循环:S=63,A=6;第6次循环:S=127,A=7;第7次循环:S=255,A=8;第9次循环:S=511,此时退出循环,
根据判断框内为跳出循环的语句
∴A<9
故选:D.
7.【解答】解:模拟程序的运行过程:
z
继续循环
x
y
循环前
/
1
1
第一圈
2
是
1
2
第二圈
3
是
2
3
第三圈
5
是
3
5
第四圈
8
是
5
8
第五圈
13
是
8
13
第六圈
21
是
13
21
第七圈
34
是
21
34
第八圈
55
是
34
55
第九圈
89
是
55
89
第十圈
144
否
此时
故选:D.
二.填空题
8.【解答】解:第一次循环,i=1,a=2;第二次循环,i=2,a=2×2+1=5;第三次循环,i=3,a=3×5+1=16;第四次循环,i=4,a=4×16+1=65>50,退出循环,此时输出的值为4
故答案为4:
9.【解答】解:程序运行过程中,各变量值变化情况如下表:1,2,1.5,0.5
第一(i=1)步:s1=s1+xi=0+1=1
第二(i=2)步:s1=s1+xi=1+2=3
第三(i=3)步:s1=s1+xi=3+1.5=4.5
第四(i=4)步:s1=s1+xi=4.5+0.5=5,s5
第五(i=5)步:i=5>4,输出s
故答案为:
10.【解答】解:由题意可知输出结果为S=28,
第1次循环,S=11,K=9,
第2次循环,S=20,K=8,
第3次循环,S=28,K=7
此时S满足输出结果,退出循环,所以判断框中的条件为k≥8.
故答案为:k≥8.
11.【解答】解:如图所示的是当型循环结构,
第一次循环:S=0,
n=1+1=2;
第二次循环:S,
n=2+1=3;
第三次循环:S,
n=3+1=4;
第四次循环:Ssin,
n=4+1=5;
第五次循环:Ssin0,
n=5+1=6;
第六次循环:S=0+sin2π=0,
n=6+1=7.
第七次循环:S=0,
n=7+1=8;
第八次循环:S,
n=8+1=9;
…
所以,S的取值的周期是6,
∵2011=335×6+1,
∴第2011次循环时,S=0,
n=2011+1=2012,
∵n=2012,n<2012不成立,
∴输出的结果S为:.
故答案为:.
12.【解答】解:由已知变量初始值为:i=1,累加变量S=0;
每次变量i递增1,而i≤10时执行程序,i>10就终止循环,输出S,
因此有S=1+2+3+4+…+10=55.
故答案为:55
13.【解答】解:i=1,m=4,满足条件i<m,j=0,满足条件j≤i,则a1,S=1+1=2;
j=1,满足条件j≤i,则a1,S=2+1=3;
j=2,不满足条件j≤i,则i=2,j=0,满足条件j≤i,则a1,S=3+1=4;
j=1,满足条件j≤i,则a2,S=4+2=6;
j=2,满足条件j≤i,则a1,S=6+1=7;
j=3,不满足条件j≤i,则i=3,j=0,满足条件j≤i,则a1,S=7+1=8;
j=1,满足条件j≤i,则a3,S=8+3=11;
j=2,满足条件j≤i,则a3,S=11+3=14;
j=3,满足条件j≤i,则a1,S=14+1=15;
j=4,不满足条件j≤i,则i=4,不满足条件i<m,输出S=15;
故答案为:15
14.【解答】解:由算法语句知,本程序是直到型循环结构的算法,
第一次循环i=1,2i=2>2000不成立;
第二次循环i=2,2i=4>2000不成立;
第三次循环i=3,2i=8>2000不成立;
第四次循环i=4,2i=16>2000不成立;
第五次循环i=5,2i=32>2000不成立;
第六次循环i=6,2i=64>2000不成立;
第七次循环i=7,2i=128>2000不成立;
第八次循环i=8,2i=256>2000不成立;
第九次循环i=9,2i=512>2000不成立;
第十次循环i=10,2i=1024>2000不成立;
第十一次循环i=11,2i=2048>2000成立,跳出循环体,i=10,输出i=10.
故答案为:10
15.【解答】解:由程序框图知:算法的功能是求S═a?b的值,
∴0?3=0,3?3=3,∴f(3)=0×3﹣3=﹣3,
当0≤x≤3时,f(x)=﹣3,
当﹣3≤x<0时,0?x=﹣x,3?x=﹣x,∴f(x)=﹣x2+x,
函数在[﹣3,0)上单调递增,∴f(x)在区间[﹣3,3]上的最小值为f(﹣3)=﹣12.
故答案为:﹣3,﹣12.
三.解答题
16.【解答】解:根据题意,第①判断框内条件成立时,按12元每张收费,
不成立时,进入第②判断框再判断,故第①判断框内应该填上:x<5?;
再看第②判断框,当条件成立时按照九折收费,不成立时按照八折收费,
因此第②判断框内应该填上x<10?,
且应该在③内填上y=0.9×12x,即y=10.8x,在④内填上y=0.8×12x,即y=9.6x
故答案为:①x<5?,②x<10?,③10.8x,④9.6x
17.【解答】解:输入语句用“INPUT”
当型循环语句用WHILE、WEND
故答案为:INPUT、WHILE、WEND
18.【解答】解:模拟执行程序,可得程序的功能是计算并输出y的值,
(1)输入X的值为0,由x<2,故y=x2=0,
故输出Y的值为0.
(2)若输出Y的值为3,y,
可解得:,或3.
19.【解答】解:(1)用辗转相除法求840与1764的最大公约数.
1764=840×2+84,840=84×10+0
∴840与1764的最大公约数是84.
(2)153﹣119=34
119﹣34=85
85﹣34=51
51﹣34=17
34﹣17=17
所以153与119的最大公约数就是17.
20.【解答】解:(1)当时,x1
而x1∈D,x2
而x2∈D,x31
而﹣1?D,退出循环,
故xi的所有项为或;
(2)数列{xn}是一个常数列,则有x1=x2=…=xn=x0即
x0=f(x0),解得:x0=1或x0=2,
所以输入的初始值x0为1或2时输出的所有xi都相等.
21.【解答】解:(1)由频率分布直方图知:众数P=75;
(2)由S←S+mifi得
S=45×0.04+55×0.06+65×0.2+75×0.3+85×0.24+95×0.16=76.2.
所以输出的S的值为76.2
22.【解答】解:(I)程序框图所使用的逻辑结构是条件结构和顺序结构;…(2分)
(Ⅱ)解析式为:f(x)(7分)
(Ⅲ)依题意得,或,或,解得x=0,或x=1,或x=3
故所求的集合为{0,1,3}.…(13分)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修三同步必刷题提高练
第一章《算法初步》
1.1
算法与程序框图
一.选择题
1.(2016?平果县模拟)在如图所示的程序框图中,输入A=22,B=4,则输出的结果是( )
A.0
B.2
C.4
D.6
2.(2016?甲卷模拟)对任意非零实数a,b,若a?b的运算原理如图所示,则20.5?log0.5的值为( )
A.
B.
C.
D.
3.(2015秋?三明期末)运行如图的程序后,输出的结果为( )
A.
B.
C.
D.
4.(2015秋?汉川市校级期末)如图给出的是计算1的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句分别是( )
A.n=n+2,i>5?
B.n=n+2,i=5?
C.n=n+1,i=5?
D.n=n+1,i>5?
5.(2016?河南模拟)右边程序框图的功能是求出的值,则框图中①、②两处应分别填写的是( )
A.i≥1,a
B.i≥1,a﹣6
C.i>1,a
D.i>1,a﹣6
6.(2012秋?莱芜期末)执行如图所示的程序框图,输出的结果是511,则判断框中应填入( )
A.A>8
B.A<8
C.A>9
D.A<9
7.阅读如图程序框图,输出的结果的值为( )
A.
B.
C.
D.
二.填空题
8.(2019?衡阳一模)阅读程序框图,运行相应的程序,则输出的值为
.
9.(2018春?沙坪坝区校级期末)某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为x1,x2,x3,x4.根据图3所示的程序框图,若知x1,x2,x3,x4分别为1,2,1.5,0.5,则输出的结果S为
.
10.(2018春?东湖区校级月考)若框图所给的程序运行结果为S=28,那么判断框中应填入的关于k的条件是
.
11.(2018?平度市校级模拟)阅读程序框图(如图),输出的结果的值为
.
12.(2018春?陆川县校级期末)给出如图的程序框图,程序输出的结果是
.
13.(2018?河南二模)将“杨辉三角”中的数从左到右、从上到下排成一数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,如图所示程序框图用来输出此数列的前若干项并求其和,若输入m=4则相应最后的输出S的值是
.
14.(2015春?城关区校级期末)下面的程序运行后,输出的值是
15.(2015春?临沂校级月考)定义某种运算?,S=a?b的运算原理如图所示.设f(x)=(0?x)x﹣(3?x).则f(3)=
;f(x)在区间[﹣3,3]上的最小值为
.
三.解答题
16.(2013秋?清流县校级月考)在某音乐唱片超市里,每张唱片售价12元,顾客如果购买5张以上(含5张)唱片,则按照九折收费;如果购买10张以上(含10张)唱片,则按照八折收费.请将下面计费的程序框图补充完整.
17.(2016秋?晋江市校级月考)把求n!的程序补充完整.
18.(2015春?郴州校级期中)已知一个程序语句如图:
(1)若输入X的值为0,求输出Y的值?
(2)若输出Y的值为3,求输入X的值?
19.(2012秋?泰宁县校级月考)(1)辗转相除法求840与1764的最大公约数;
(2)更相减损术求153与119的最大公约数.
20.(2019春?北海期中)在如图所示的程序框图中,有这样一个执行框xi=f(xi﹣1),其中的函数关系式为f(x),程序框图中的D为函数f(x)的定义域.
(1)若输入x0,请写出输出的所有x的值;
(2)若输出的所有xi都相等,试求输入的初始值x0.
21.(2016秋?松桃县校级期中)从高二抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.
试利用频率分布直方图(图1),求(精确到小数点后一位):
(1)估算这50名学生成绩的众数;
(2)在上述统计数据的分析中有一项计算见算法流程图(图2),求输出S的值.(注:mi,fi分别是第i组分数的组中值和频率).
22.(2016春?鼓楼区期中)如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(Ⅲ)若要使输入的x的值与输出的y的值相等,则输入x的值的集合为多少?
参考答案与试题解析
一.选择题
1.【解答】解:当B=4,满足进行循环的条件,C=2,A=4,B=2,
当B=2,满足进行循环的条件,C=0,A=2,B=0,
当B=0,不满足进行循环的条件,
故输出的A值为2,
故选:B.
2.【解答】解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算分段函数y函数值,
∵20.5?log0.5?2,
此时ab=2,
∴y.
故选:C.
3.【解答】解:根据程序语言的运行过程,得
该程序运行后输出的是S;
计算S=(1)+()+()+()+()=1.
所以输出S.
故选:C.
4.【解答】解:模拟程序框图的运行过程,知;
①处表示各项的分母变化过程,
而分母相差为2,
∴n=n+2;
②处为直到型循环结构满足跳出循环体的条件,
而分母从1到9共5项,
∴i>5?.
故选:A.
5.【解答】解:程序框图是计算的值,
则利用累积加,则第一个处理框应为i>1,然后计算i是增加1个,i=i+1,
第二空输出结果a﹣6.
故选:D.
6.【解答】解:经判断此循环为“直到型“结构,判断框内为跳出循环的语句
第1次循环:S=3,A=2;第2次循环:S=7,A=3;第3次循环:S=15,A=4;第4次循环:S=31,A=5;第5次循环:S=63,A=6;第6次循环:S=127,A=7;第7次循环:S=255,A=8;第9次循环:S=511,此时退出循环,
根据判断框内为跳出循环的语句
∴A<9
故选:D.
7.【解答】解:模拟程序的运行过程:
z
继续循环
x
y
循环前
/
1
1
第一圈
2
是
1
2
第二圈
3
是
2
3
第三圈
5
是
3
5
第四圈
8
是
5
8
第五圈
13
是
8
13
第六圈
21
是
13
21
第七圈
34
是
21
34
第八圈
55
是
34
55
第九圈
89
是
55
89
第十圈
144
否
此时
故选:D.
二.填空题
8.【解答】解:第一次循环,i=1,a=2;第二次循环,i=2,a=2×2+1=5;第三次循环,i=3,a=3×5+1=16;第四次循环,i=4,a=4×16+1=65>50,退出循环,此时输出的值为4
故答案为4:
9.【解答】解:程序运行过程中,各变量值变化情况如下表:1,2,1.5,0.5
第一(i=1)步:s1=s1+xi=0+1=1
第二(i=2)步:s1=s1+xi=1+2=3
第三(i=3)步:s1=s1+xi=3+1.5=4.5
第四(i=4)步:s1=s1+xi=4.5+0.5=5,s5
第五(i=5)步:i=5>4,输出s
故答案为:
10.【解答】解:由题意可知输出结果为S=28,
第1次循环,S=11,K=9,
第2次循环,S=20,K=8,
第3次循环,S=28,K=7
此时S满足输出结果,退出循环,所以判断框中的条件为k≥8.
故答案为:k≥8.
11.【解答】解:如图所示的是当型循环结构,
第一次循环:S=0,
n=1+1=2;
第二次循环:S,
n=2+1=3;
第三次循环:S,
n=3+1=4;
第四次循环:Ssin,
n=4+1=5;
第五次循环:Ssin0,
n=5+1=6;
第六次循环:S=0+sin2π=0,
n=6+1=7.
第七次循环:S=0,
n=7+1=8;
第八次循环:S,
n=8+1=9;
…
所以,S的取值的周期是6,
∵2011=335×6+1,
∴第2011次循环时,S=0,
n=2011+1=2012,
∵n=2012,n<2012不成立,
∴输出的结果S为:.
故答案为:.
12.【解答】解:由已知变量初始值为:i=1,累加变量S=0;
每次变量i递增1,而i≤10时执行程序,i>10就终止循环,输出S,
因此有S=1+2+3+4+…+10=55.
故答案为:55
13.【解答】解:i=1,m=4,满足条件i<m,j=0,满足条件j≤i,则a1,S=1+1=2;
j=1,满足条件j≤i,则a1,S=2+1=3;
j=2,不满足条件j≤i,则i=2,j=0,满足条件j≤i,则a1,S=3+1=4;
j=1,满足条件j≤i,则a2,S=4+2=6;
j=2,满足条件j≤i,则a1,S=6+1=7;
j=3,不满足条件j≤i,则i=3,j=0,满足条件j≤i,则a1,S=7+1=8;
j=1,满足条件j≤i,则a3,S=8+3=11;
j=2,满足条件j≤i,则a3,S=11+3=14;
j=3,满足条件j≤i,则a1,S=14+1=15;
j=4,不满足条件j≤i,则i=4,不满足条件i<m,输出S=15;
故答案为:15
14.【解答】解:由算法语句知,本程序是直到型循环结构的算法,
第一次循环i=1,2i=2>2000不成立;
第二次循环i=2,2i=4>2000不成立;
第三次循环i=3,2i=8>2000不成立;
第四次循环i=4,2i=16>2000不成立;
第五次循环i=5,2i=32>2000不成立;
第六次循环i=6,2i=64>2000不成立;
第七次循环i=7,2i=128>2000不成立;
第八次循环i=8,2i=256>2000不成立;
第九次循环i=9,2i=512>2000不成立;
第十次循环i=10,2i=1024>2000不成立;
第十一次循环i=11,2i=2048>2000成立,跳出循环体,i=10,输出i=10.
故答案为:10
15.【解答】解:由程序框图知:算法的功能是求S═a?b的值,
∴0?3=0,3?3=3,∴f(3)=0×3﹣3=﹣3,
当0≤x≤3时,f(x)=﹣3,
当﹣3≤x<0时,0?x=﹣x,3?x=﹣x,∴f(x)=﹣x2+x,
函数在[﹣3,0)上单调递增,∴f(x)在区间[﹣3,3]上的最小值为f(﹣3)=﹣12.
故答案为:﹣3,﹣12.
三.解答题
16.【解答】解:根据题意,第①判断框内条件成立时,按12元每张收费,
不成立时,进入第②判断框再判断,故第①判断框内应该填上:x<5?;
再看第②判断框,当条件成立时按照九折收费,不成立时按照八折收费,
因此第②判断框内应该填上x<10?,
且应该在③内填上y=0.9×12x,即y=10.8x,在④内填上y=0.8×12x,即y=9.6x
故答案为:①x<5?,②x<10?,③10.8x,④9.6x
17.【解答】解:输入语句用“INPUT”
当型循环语句用WHILE、WEND
故答案为:INPUT、WHILE、WEND
18.【解答】解:模拟执行程序,可得程序的功能是计算并输出y的值,
(1)输入X的值为0,由x<2,故y=x2=0,
故输出Y的值为0.
(2)若输出Y的值为3,y,
可解得:,或3.
19.【解答】解:(1)用辗转相除法求840与1764的最大公约数.
1764=840×2+84,840=84×10+0
∴840与1764的最大公约数是84.
(2)153﹣119=34
119﹣34=85
85﹣34=51
51﹣34=17
34﹣17=17
所以153与119的最大公约数就是17.
20.【解答】解:(1)当时,x1
而x1∈D,x2
而x2∈D,x31
而﹣1?D,退出循环,
故xi的所有项为或;
(2)数列{xn}是一个常数列,则有x1=x2=…=xn=x0即
x0=f(x0),解得:x0=1或x0=2,
所以输入的初始值x0为1或2时输出的所有xi都相等.
21.【解答】解:(1)由频率分布直方图知:众数P=75;
(2)由S←S+mifi得
S=45×0.04+55×0.06+65×0.2+75×0.3+85×0.24+95×0.16=76.2.
所以输出的S的值为76.2
22.【解答】解:(I)程序框图所使用的逻辑结构是条件结构和顺序结构;…(2分)
(Ⅱ)解析式为:f(x)(7分)
(Ⅲ)依题意得,或,或,解得x=0,或x=1,或x=3
故所求的集合为{0,1,3}.…(13分)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
