第二章《统计》2.2 用样本估计总体(基础练,含解析)—2020-2021学年人教A版必修三同步必刷题
文档属性
| 名称 | 第二章《统计》2.2 用样本估计总体(基础练,含解析)—2020-2021学年人教A版必修三同步必刷题 | 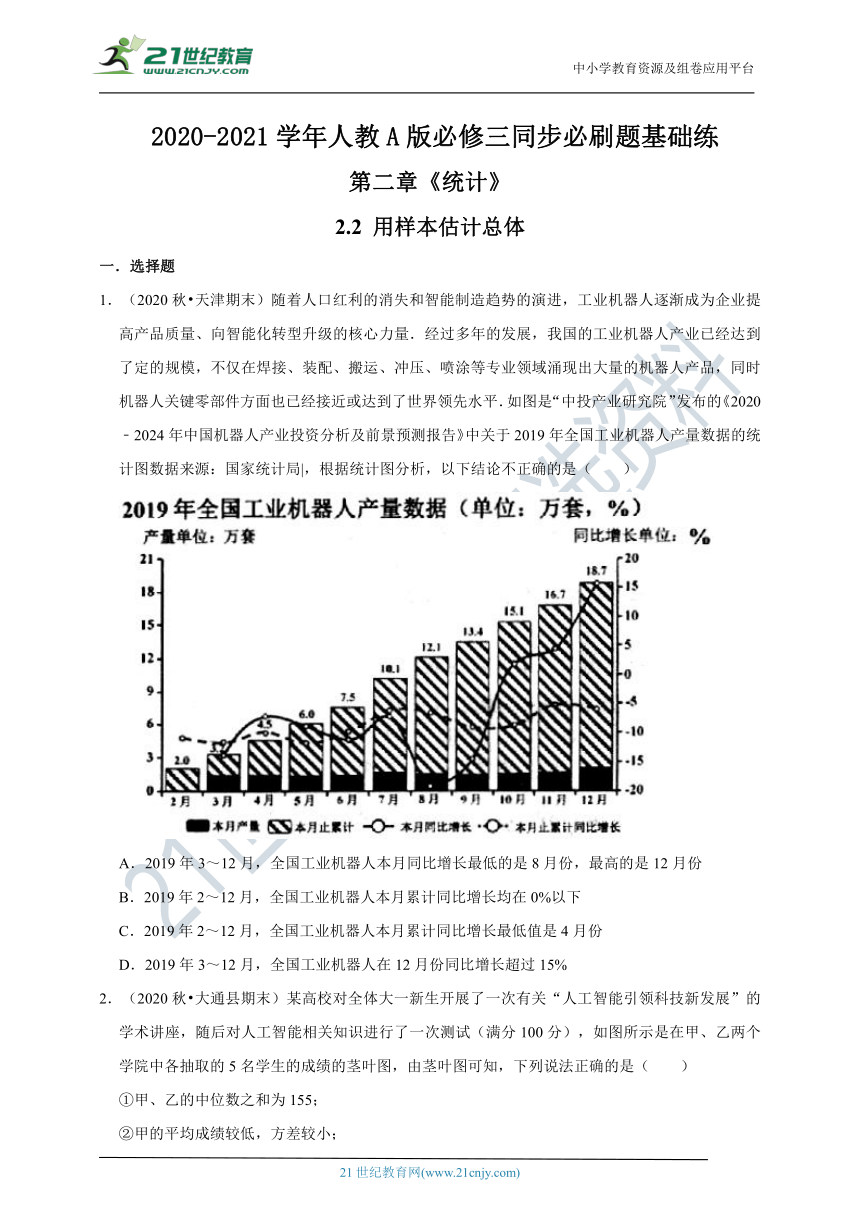 | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 23:38:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修三同步必刷题基础练
第二章《统计》
2.2
用样本估计总体
一.选择题
1.(2020秋?天津期末)随着人口红利的消失和智能制造趋势的演进,工业机器人逐渐成为企业提高产品质量、向智能化转型升级的核心力量.经过多年的发展,我国的工业机器人产业已经达到了定的规模,不仅在焊接、装配、搬运、冲压、喷涂等专业领域涌现出大量的机器人产品,同时机器人关键零部件方面也已经接近或达到了世界领先水平.如图是“中投产业研究院”发布的《2020﹣2024年中国机器人产业投资分析及前景预测报告》中关于2019年全国工业机器人产量数据的统计图数据来源:国家统计局|,根据统计图分析,以下结论不正确的是( )
A.2019年3~12月,全国工业机器人本月同比增长最低的是8月份,最高的是12月份
B.2019年2~12月,全国工业机器人本月累计同比增长均在0%以下
C.2019年2~12月,全国工业机器人本月累计同比增长最低值是4月份
D.2019年3~12月,全国工业机器人在12月份同比增长超过15%
2.(2020秋?大通县期末)某高校对全体大一新生开展了一次有关“人工智能引领科技新发展”的学术讲座,随后对人工智能相关知识进行了一次测试(满分100分),如图所示是在甲、乙两个学院中各抽取的5名学生的成绩的茎叶图,由茎叶图可知,下列说法正确的是( )
①甲、乙的中位数之和为155;
②甲的平均成绩较低,方差较小;
③甲的平均成绩较低,方差较大;
④乙的平均成绩较高,方差较小;
⑤乙的平均成绩较高,方差较大
A.①②④
B.①③④
C.①③⑤
D.②⑤
3.(2020秋?辽宁期末)已知数据x1,x2,…,xn,t的平均数为t,方差为s12,数据x1,x2,…,xn的方差为s22,则( )
A.s12>s22
B.s12=s22
C.s12<s22
D.s12与s22的大小关系无法判断
4.(2020秋?和平区期末)已知某校一次数学测验所有学生得分都在[80,150]内,根据学生得分情况绘制的频率分布直方图如图所示,则图中a的值是( )
A.0.015
B.0.020
C.0.030
D.0.040
5.(2020秋?思明区校级月考)如图①、②分别是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大
B.乙户比甲户大
C.甲、乙两户一般大
D.无法确定哪一户大
6.(2021?郑州一模)某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论错误的是( )
注:90后指1990年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后一定比80前多
D.互联网行业中从事技术岗位的人数90后一定比80后多
7.(2021?郑州一模)调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列所有正确结论的编号是( )
注:90后指1900年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
①互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
②互联网行业中从事技术岗位的人数超过总人数的20%
③互联网行业中从事运营岗位的人数90后比80前多
④互联网行业中从事技术岗位的人数90后比80后多
A.①②③
B.①②④
C.①③④
D.②③④
二.填空题
8.(2020秋?辽宁期末)甲、乙两位同学高三8次物理模拟考试成绩如图所示,甲同学的平均成绩与乙同学的众数相等,则m=
.
9.(2021?十九模拟)某小区物业为了让居民更好地对垃圾进行分类,决定对小区居民进行培训,并从培训的学员中随机抽取了50名进行培训结果测试,物业将这50名学员的成绩(满分100分)按照[50,60),[60,70),…,[90,100]分成了5组,并制成了如图所示的频率分布直方图,则这50名学员的平均成绩为
分(每组数以该组区间的中点值作代表).
10.(2021?三模拟)随着现在短视频App的推行,很多人都喜欢看有特色的短视频.现对某小区居民使用“抖音APP”观看短视频的情况进行统计,有20个人的使用率为0.9,有20个人的使用率为0.8,有10个人的使用率为0.6,则该小区居民“抖音APP”的平均使用率的估计值为
.
11.(2021?长宁区一模)数组2.7、3.1、2.5、4.8、2.9、3.6的中位数为
.
12.(2021?十二模拟)2019年11月12日,中国人民银行首次发布双十一“剁手”数据,全国居民人均消费超过1000元.某调查机构调查某地区不同年龄段的居民人均消费情况,得到如图所示的扇形统计图.已知年龄小于25岁的居民人均消费700元,则年龄在25~35岁之间的居民人均消费
元.
13.(2021?八模拟)疫情期间,某校高一(1)班组织团员参加志愿者捐款活动,该班级40名团员参加捐款活动的数额(单位:元)统计如表:
数额
30
40
50
60
人数
5
20
10
5
则平均每人捐款的数额为
.
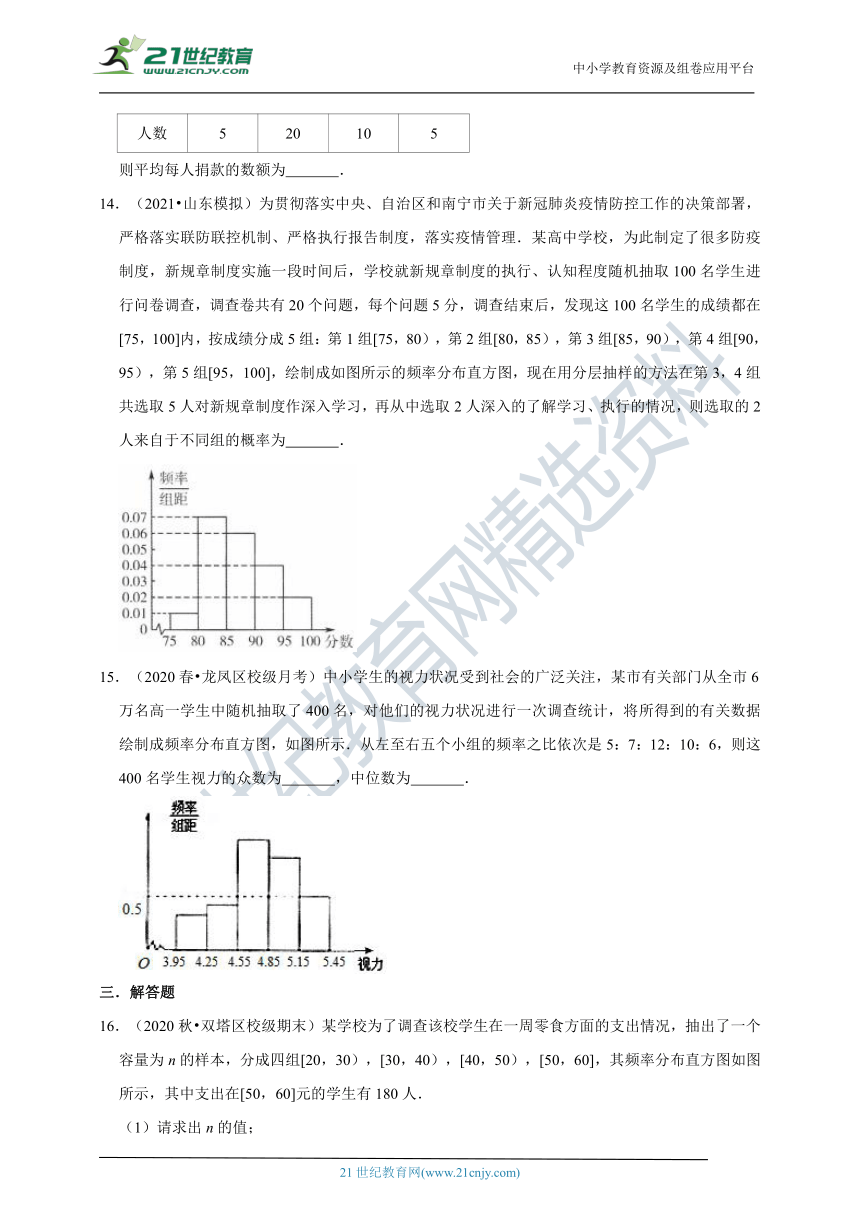
14.(2021?山东模拟)为贯彻落实中央、自治区和南宁市关于新冠肺炎疫情防控工作的决策部署,严格落实联防联控机制、严格执行报告制度,落实疫情管理.某高中学校,为此制定了很多防疫制度,新规章制度实施一段时间后,学校就新规章制度的执行、认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,现在用分层抽样的方法在第3,4组共选取5人对新规章制度作深入学习,再从中选取2人深入的了解学习、执行的情况,则选取的2人来自于不同组的概率为
.
15.(2020春?龙凤区校级月考)中小学生的视力状况受到社会的广泛关注,某市有关部门从全市6万名高一学生中随机抽取了400名,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示.从左至右五个小组的频率之比依次是5:7:12:10:6,则这400名学生视力的众数为
,中位数为
.
三.解答题
16.(2020秋?双塔区校级期末)某学校为了调查该校学生在一周零食方面的支出情况,抽出了一个容量为n的样本,分成四组[20,30),[30,40),[40,50),[50,60],其频率分布直方图如图所示,其中支出在[50,60]元的学生有180人.
(1)请求出n的值;
(2)请以样本估计全校学生的平均支出为多少元(同一组的数据用该区间的中点值作代表);
(3)如果采用分层抽样的方法从[30,40),[40,50)共抽取5人,然后从中选取2人参加学校进一步的座谈会,求在[30,40),[40,50)中正好各抽取一人的概率为多少.
17.(2021?一模拟)从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.
(Ⅰ)求直方图中x的值;
(Ⅱ)(ⅰ)求在这些用户中,用电量在区间[100,250)内的居民数;
(ⅱ)如果按分层抽样方法,在这些用户中按1:10的比例抽取用户进一步调查,那么用电量在[150,200)内的居民数应抽取多少?
18.(2020秋?番禺区校级期中)今年年初,一场突如其来的新型冠状病毒感染的肺炎疫情牵动着亿万人民的心,疫情发生后,党中央、国务院高度重视,习近平总书记强调,生命重于素山,疫情就是命令,防控就是责任,把人民群众生命安全和身体健康放在第一位,把疫情防控作为当前最重要的工作来抓.某市为增强市民的防疫保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在该6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组志愿者有人被抽中的概率.
19.(2020春?海珠区校级月考)新冠肺炎疫情在我国爆发以来,我国举国上下众志成城、团结一致抗击新冠肺炎疫情,经过两个月的努力,我国的疫情已经得到有效控制,武汉也在逐渐恢复往日的活力.为了解大众对新冠肺炎相关知识的掌握情况,某网站发布了调查问卷,问卷满分100分,并搜集到50份问卷反馈表.根据这50份问卷得分情况,绘制了频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100).
(1)求频率分布直方图中a的值;
(2)由频率分布直方图估计评分的中位数(保留两位小数)与平均数;
(3)从评分在[40,60)的观影者中随机抽取2人,求至少有一人评分在[40,50)的概率.
20.(2020秋?锦州期末)某中学高一年级举行了一次数学竞赛,从中随机抽取了一批学生的成绩,经统计,这批学生的成绩全部介于50至100之间,将数据按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示.
(1)求频率分布直方图中a的值;
(2)若从高一学生中随机抽取一人,估计这名学生数学竞赛成绩不低于80分的概率;
(3)假设同组中的每个数据都用该组区间的中点值代替,估计高一年级学生本次数学竞赛的平均分.
21.(2020秋?大连期末)我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,1),[1,2),[2,3),[3,4),[4,5]分成5组,制成了如图所示的频率分布直方图.
(Ⅰ)求图中a的值;
(Ⅱ)假设同组中的每个数据都用该组区间的中值点代替,估计全市家庭月均用水量的平均数.
22.(2020秋?辽宁期末)某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:每一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.
(1)估计此次百米测试成绩的中位数(精确到001);
(2)为了尽快提高学生的体育成绩,对此次百米测试成绩不小于17秒的两组同学进行特训,特训一段时间后有两位同学成绩符合要求,求这两位同学来自同一组的概率.
23.(2020秋?秦安县校级期末)某单位对三个车间的人数统计情况如表:用分层抽样的方法从三个车间抽取30人,其中三车间有12人.
一车间
二车间
三车间
男职工
200
100
250
女职工
600
k
550
(1)求k的值.
(2)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,则75对应的编号是多少?并求这五个人加班天数的方差.
参考答案与试题解析
一.选择题
1.【解答】解:由《2020﹣2024年中国机器人产业投资分析及前景预测报告》中关于2019年全国工业机器人产量数据的统计图,知:
对于A,由本月同比增长拆线图得:
2019年3~12月,全国工业机器人本月同比增长最低的是8月份,最高的是12月份,故A正确;
对于B,由本月累计同比增长拆线图得:
2019年2~12月,全国工业机器人本月累计同比增长均在0%以下,故B正确;
对于C,由本月同比增长拆线图得:
2019年2~12月,全国工业机器人本月累计同比增长最低值是8月份,故C错误;
对于D,2019年3~12月,全国工业机器人在12月份同比增长超过15%,故D正确.
故选:C.
2.【解答】解:由茎叶图可得甲、乙两组数据的中位数分别为76,79,
∴甲、乙的中位数之和为155,故①正确;
78,
81,
[(63﹣78)2+(72﹣78)2+(76﹣78)2+(83﹣78)2+(96﹣78)2]=122.8,
.
故②错误,③正确,④正确,⑤错误.
所以正确的说法是①③④.
故选:B.
3.【解答】解:由t,得x1+x2+…+xn+t=t(n+1),
所以x1+x2+…+xn=tn,所以t,
故两组数据的平均数都是t,
则[(t﹣t)2],
[],
∵,∴,
故选:C.
4.【解答】解:由频率分布直方图可得(0.003+0.007+0.012+2a+0.03+0.008)×10=1,
解得a=0.020.
故选:B.
5.【解答】解:由题意,根据条形图,可得甲户教育支出占,
由饼形图,可得乙户教育支出占25%.可得25%>20%.
所以乙户全年总支出的百分比比甲户全年总支出的百分比大.
故选:B.
6.【解答】解:由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×(39.6%+17%)=31.696%>30%,
互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上,故A正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%>20%,
互联网行业中从事技术岗位的人数超过总人数的20%,故B正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
17%×56%=9.52%>3%,
互联网行业中从事运营岗位的人数90后比80前多,故C正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%<41%,
互联网行业中从事技术岗位的人数90后不一定比80后多,故D错误.
故选:D.
7.【解答】解:由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×(39.6%+17%)=31.696%>30%,
互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上,故①正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%>20%,
互联网行业中从事技术岗位的人数超过总人数的20%,故②正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
17%×56%=9.52%>3%,
互联网行业中从事运营岗位的人数90后比80前多,故③正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%<41%,
互联网行业中从事技术岗位的人数90后不一定比80后多,故④错误.
故正确结论的编号是①②③.
故选:A.
二.填空题
8.【解答】解:由茎叶图知,甲同学的平均成绩与乙同学的众数相等,
即(73+79+82+85+80+m+83+92+93)=84,
解得m=5.
故答案为:5.
9.【解答】解:由频率分布直方图得成绩在[80,90)的频率为:
1﹣(0.01+0.03+0.03+0.01)×10=0.2.
解得x=0.02,
∴这50名学员的平均成绩为:
(55×0.01+65×0.03+75×0.03+85×0.02+95×0.01)×10=74(分).
故答案为:74.
10.【解答】解:该小区居民“抖音APP”的平均使用率的估计值:
0.8,
故答案为:0.8.
11.【解答】解:该组数据按从小到大排列为:2.5,2.7,2.9,3.1,3.6,4.8;
所以这组数据的中位数为
(2.9+3.1)=3.0.
故答案为:3.0.
12.【解答】解:由图可知,年龄在25~35岁之间所对应的扇形圆心角为360°﹣70°﹣130°=160°,
所以年龄小于25岁、年龄在25~35岁之间、年龄大于35岁的居民人均消费之比为70°:160°:130°=7:16:13.
设年龄在25~35岁之间的居民人均消费x元,
则,解得x=1600.
则年龄在25~35岁之间的居民人均消费1600元.
故答案为:1600.
13.【解答】解:利用平均数公式可得这组数据的平均数为:
43.75(元).
故答案为:43.75元.
14.【解答】解:由题可知第3组的人数为0.06×5×100=30;第4组的人数为0.04×5×100=20.
现在用分层抽样的方法在第3,4组共50人中选取5人对新规章制度作深入学习,即抽取比例为,
则采用分层抽样在两组中选取的人数分别为3,2,
则选取的2人来自于不同组的概率为,
故答案为:.
15.【解答】解:由图可知,众数为(4.55+4.85)÷2=4.7;
第五组的频率为0.5×0.3=0.15;
从左至右五个小组的频率之比依次是5:7:12:10:6,可得,
第一小组的频率为0.125;
第二小组的频率为;
第三小组的频率为;
所以中位数在第三小组,第三小组矩形面积为0.3,
则第三小组的高为,
设中位数为x,则0.125+0.175+(x﹣4.55)×1=0.5,
解得x=4.75.
故答案为:4.7,4.75
三.解答题
16.【解答】解:(1)支出在[50,60]元的学生的频率为:1﹣(0.01+0.024+0.036)×10=0.3,
所以,n600;
(2)由频率分布直方图可知,平均支出为:25×0.01×10+35×0.024×10+45×0.036×10+55×0.03×10=43.6;
(3)由题意可知[30,40),[40,50)分别有600×0.024×10=144,600×0.036×10=216,故在[30,40)中抽取2人,在[40,50)中抽取3人,
设事件A为:在[30,40),[40,50)中正好各抽取一人,则P(A).
17.【解答】解:(Ⅰ)由频率分布直方图得:
(0.0012+0.0024×2+0.0036+x+0.0060)×50=1,
解得直方图中x=0.0044.
(Ⅱ)(ⅰ)用电量在[100,250)内的频率为:
(0.0036+0.0060+0.0044)×50=0.7,
∴在这些用户中,用电量在区间[100,250)内的居民数为100×0.7=70户.
(ⅱ)用电量在[150,200)内的户数为0.0060×50×100=30(户),
按分层抽样方法,在这些用户中按1:10的比例抽取用户进一步调查,
用电量在[150,200)内的居民数应该抽取:303(户).
18.【解答】解:(1)从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,
应从第3组抽取:63名志愿者,
从第4组抽取:62名志愿者,
从第5组抽取:61名志愿者.
(2)在(1)的条件下,该市决定在该6名志愿者中随机抽取2名志愿者介绍宣传经验,
基本事件总数n15,
第4组志愿者有人被抽中包含的基本事件个数m9,
∴第4组志愿者有人被抽中的概率P.
19.【解答】解:(1)由频率分布直方图得:
(0.004+a+0.022+0.028+0.022+0.018)×10=1,
解得a=0.006.
(2)由频率分布直方图得:
[40,70)的频率为:(0.004+0.006+0.022)×10=0.32,
[70,80)的频率为:0.028×10=0.28,
∴估计评分的中位数为:
7070.64.
平均数为:45×0.004×10+55×0.006×10+65×0.022×10+75×0.028×10+85×0.022×10+95×0.018×10=76.2.
(3)评分在[40,50)的观影者有:0.004×10×50=2人,评分在[50,60)的观影者有0.006×10×50=3人,
从评分在[40,60)的观影者中随机抽取2人,基本事件总数n10,
至少有一人评分在[40,50)包含的基本事件个数m7,
∴至少有一人评分在[40,50)的概率P.
20.【解答】解:(1)由题意可知(0.005+0.030+0.035+a+0.010)×10=1,
解得a=0.020.
(2)抽取的样本中,
成绩不低于80分的学生所占的比例是(a+0.010)×10=(0.020+0.010)×10=0.3,
所以若从高一学生中随机抽取一人,
估计这名学生数学竞赛成绩不低于80分的概率为0.3.
(3)因为(55×0.005+65×0.030+75×0.035+85×0.020+95×0.010)×10=75,
因此估计高一年级学生本次数学竞赛的平均分为75.
21.【解答】解:(Ⅰ)由频率和为1,得a=1﹣0.12﹣0.22﹣0.36﹣0.12=0.18.
(Ⅱ)计算平均数为0.5×0.12+1.5×0.22+2.5×0.36+3.5×0.18+4.5×0.12=2.46(t),
估计全市家庭月均用水量的平均数为2.46t.
22.【解答】解:(1)前两组的概率和为0.02+0.18=0.2,前三组的概率和为0.02+0.18+036=0.56,
所以0.5﹣0.2=0.3,
故中位数为1515.83;
(2)由已知记第五组的频数为50×0.06×1=3,同理第六组的频数为2,
记第五组的学生为a1,a2,a3,第六组的学生为b1,b2,
因为不小于17秒的两组同学进行特训,特训一段时间后有两位同学成绩符合要求,
则样本空间中所有基本事件为Ω={(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}
共10个样本点,
记事件A:两位同学来自同一组,则
A={(a1,a2),(a1,a3),(a2,a3),(b1,b2)}共4个基本事件样本点;
故P(A).
故这两位同学来自同一组的概率为.
23.【解答】解:(1)由题意得,解得k=300;
(2)由题意得,抽取间距d40,
设75对应的编号是m,则145=m+(4﹣1)×40,m=25,
所以75对应的编号是25,
故(75+79+82+73+81)=78,
s2[(75﹣78)2+(79﹣78)2+(82﹣78)2+(73﹣78)2+(81﹣78)2]=12.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修三同步必刷题基础练
第二章《统计》
2.2
用样本估计总体
一.选择题
1.(2020秋?天津期末)随着人口红利的消失和智能制造趋势的演进,工业机器人逐渐成为企业提高产品质量、向智能化转型升级的核心力量.经过多年的发展,我国的工业机器人产业已经达到了定的规模,不仅在焊接、装配、搬运、冲压、喷涂等专业领域涌现出大量的机器人产品,同时机器人关键零部件方面也已经接近或达到了世界领先水平.如图是“中投产业研究院”发布的《2020﹣2024年中国机器人产业投资分析及前景预测报告》中关于2019年全国工业机器人产量数据的统计图数据来源:国家统计局|,根据统计图分析,以下结论不正确的是( )
A.2019年3~12月,全国工业机器人本月同比增长最低的是8月份,最高的是12月份
B.2019年2~12月,全国工业机器人本月累计同比增长均在0%以下
C.2019年2~12月,全国工业机器人本月累计同比增长最低值是4月份
D.2019年3~12月,全国工业机器人在12月份同比增长超过15%
2.(2020秋?大通县期末)某高校对全体大一新生开展了一次有关“人工智能引领科技新发展”的学术讲座,随后对人工智能相关知识进行了一次测试(满分100分),如图所示是在甲、乙两个学院中各抽取的5名学生的成绩的茎叶图,由茎叶图可知,下列说法正确的是( )
①甲、乙的中位数之和为155;
②甲的平均成绩较低,方差较小;
③甲的平均成绩较低,方差较大;
④乙的平均成绩较高,方差较小;
⑤乙的平均成绩较高,方差较大
A.①②④
B.①③④
C.①③⑤
D.②⑤
3.(2020秋?辽宁期末)已知数据x1,x2,…,xn,t的平均数为t,方差为s12,数据x1,x2,…,xn的方差为s22,则( )
A.s12>s22
B.s12=s22
C.s12<s22
D.s12与s22的大小关系无法判断
4.(2020秋?和平区期末)已知某校一次数学测验所有学生得分都在[80,150]内,根据学生得分情况绘制的频率分布直方图如图所示,则图中a的值是( )
A.0.015
B.0.020
C.0.030
D.0.040
5.(2020秋?思明区校级月考)如图①、②分别是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大
B.乙户比甲户大
C.甲、乙两户一般大
D.无法确定哪一户大
6.(2021?郑州一模)某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论错误的是( )
注:90后指1990年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后一定比80前多
D.互联网行业中从事技术岗位的人数90后一定比80后多
7.(2021?郑州一模)调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列所有正确结论的编号是( )
注:90后指1900年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
①互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
②互联网行业中从事技术岗位的人数超过总人数的20%
③互联网行业中从事运营岗位的人数90后比80前多
④互联网行业中从事技术岗位的人数90后比80后多
A.①②③
B.①②④
C.①③④
D.②③④
二.填空题
8.(2020秋?辽宁期末)甲、乙两位同学高三8次物理模拟考试成绩如图所示,甲同学的平均成绩与乙同学的众数相等,则m=
.
9.(2021?十九模拟)某小区物业为了让居民更好地对垃圾进行分类,决定对小区居民进行培训,并从培训的学员中随机抽取了50名进行培训结果测试,物业将这50名学员的成绩(满分100分)按照[50,60),[60,70),…,[90,100]分成了5组,并制成了如图所示的频率分布直方图,则这50名学员的平均成绩为
分(每组数以该组区间的中点值作代表).
10.(2021?三模拟)随着现在短视频App的推行,很多人都喜欢看有特色的短视频.现对某小区居民使用“抖音APP”观看短视频的情况进行统计,有20个人的使用率为0.9,有20个人的使用率为0.8,有10个人的使用率为0.6,则该小区居民“抖音APP”的平均使用率的估计值为
.
11.(2021?长宁区一模)数组2.7、3.1、2.5、4.8、2.9、3.6的中位数为
.
12.(2021?十二模拟)2019年11月12日,中国人民银行首次发布双十一“剁手”数据,全国居民人均消费超过1000元.某调查机构调查某地区不同年龄段的居民人均消费情况,得到如图所示的扇形统计图.已知年龄小于25岁的居民人均消费700元,则年龄在25~35岁之间的居民人均消费
元.
13.(2021?八模拟)疫情期间,某校高一(1)班组织团员参加志愿者捐款活动,该班级40名团员参加捐款活动的数额(单位:元)统计如表:
数额
30
40
50
60
人数
5
20
10
5
则平均每人捐款的数额为
.
14.(2021?山东模拟)为贯彻落实中央、自治区和南宁市关于新冠肺炎疫情防控工作的决策部署,严格落实联防联控机制、严格执行报告制度,落实疫情管理.某高中学校,为此制定了很多防疫制度,新规章制度实施一段时间后,学校就新规章制度的执行、认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,现在用分层抽样的方法在第3,4组共选取5人对新规章制度作深入学习,再从中选取2人深入的了解学习、执行的情况,则选取的2人来自于不同组的概率为
.
15.(2020春?龙凤区校级月考)中小学生的视力状况受到社会的广泛关注,某市有关部门从全市6万名高一学生中随机抽取了400名,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示.从左至右五个小组的频率之比依次是5:7:12:10:6,则这400名学生视力的众数为
,中位数为
.
三.解答题
16.(2020秋?双塔区校级期末)某学校为了调查该校学生在一周零食方面的支出情况,抽出了一个容量为n的样本,分成四组[20,30),[30,40),[40,50),[50,60],其频率分布直方图如图所示,其中支出在[50,60]元的学生有180人.
(1)请求出n的值;
(2)请以样本估计全校学生的平均支出为多少元(同一组的数据用该区间的中点值作代表);
(3)如果采用分层抽样的方法从[30,40),[40,50)共抽取5人,然后从中选取2人参加学校进一步的座谈会,求在[30,40),[40,50)中正好各抽取一人的概率为多少.
17.(2021?一模拟)从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.
(Ⅰ)求直方图中x的值;
(Ⅱ)(ⅰ)求在这些用户中,用电量在区间[100,250)内的居民数;
(ⅱ)如果按分层抽样方法,在这些用户中按1:10的比例抽取用户进一步调查,那么用电量在[150,200)内的居民数应抽取多少?
18.(2020秋?番禺区校级期中)今年年初,一场突如其来的新型冠状病毒感染的肺炎疫情牵动着亿万人民的心,疫情发生后,党中央、国务院高度重视,习近平总书记强调,生命重于素山,疫情就是命令,防控就是责任,把人民群众生命安全和身体健康放在第一位,把疫情防控作为当前最重要的工作来抓.某市为增强市民的防疫保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在该6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组志愿者有人被抽中的概率.
19.(2020春?海珠区校级月考)新冠肺炎疫情在我国爆发以来,我国举国上下众志成城、团结一致抗击新冠肺炎疫情,经过两个月的努力,我国的疫情已经得到有效控制,武汉也在逐渐恢复往日的活力.为了解大众对新冠肺炎相关知识的掌握情况,某网站发布了调查问卷,问卷满分100分,并搜集到50份问卷反馈表.根据这50份问卷得分情况,绘制了频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100).
(1)求频率分布直方图中a的值;
(2)由频率分布直方图估计评分的中位数(保留两位小数)与平均数;
(3)从评分在[40,60)的观影者中随机抽取2人,求至少有一人评分在[40,50)的概率.
20.(2020秋?锦州期末)某中学高一年级举行了一次数学竞赛,从中随机抽取了一批学生的成绩,经统计,这批学生的成绩全部介于50至100之间,将数据按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示.
(1)求频率分布直方图中a的值;
(2)若从高一学生中随机抽取一人,估计这名学生数学竞赛成绩不低于80分的概率;
(3)假设同组中的每个数据都用该组区间的中点值代替,估计高一年级学生本次数学竞赛的平均分.
21.(2020秋?大连期末)我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,1),[1,2),[2,3),[3,4),[4,5]分成5组,制成了如图所示的频率分布直方图.
(Ⅰ)求图中a的值;
(Ⅱ)假设同组中的每个数据都用该组区间的中值点代替,估计全市家庭月均用水量的平均数.
22.(2020秋?辽宁期末)某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:每一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.
(1)估计此次百米测试成绩的中位数(精确到001);
(2)为了尽快提高学生的体育成绩,对此次百米测试成绩不小于17秒的两组同学进行特训,特训一段时间后有两位同学成绩符合要求,求这两位同学来自同一组的概率.
23.(2020秋?秦安县校级期末)某单位对三个车间的人数统计情况如表:用分层抽样的方法从三个车间抽取30人,其中三车间有12人.
一车间
二车间
三车间
男职工
200
100
250
女职工
600
k
550
(1)求k的值.
(2)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,则75对应的编号是多少?并求这五个人加班天数的方差.
参考答案与试题解析
一.选择题
1.【解答】解:由《2020﹣2024年中国机器人产业投资分析及前景预测报告》中关于2019年全国工业机器人产量数据的统计图,知:
对于A,由本月同比增长拆线图得:
2019年3~12月,全国工业机器人本月同比增长最低的是8月份,最高的是12月份,故A正确;
对于B,由本月累计同比增长拆线图得:
2019年2~12月,全国工业机器人本月累计同比增长均在0%以下,故B正确;
对于C,由本月同比增长拆线图得:
2019年2~12月,全国工业机器人本月累计同比增长最低值是8月份,故C错误;
对于D,2019年3~12月,全国工业机器人在12月份同比增长超过15%,故D正确.
故选:C.
2.【解答】解:由茎叶图可得甲、乙两组数据的中位数分别为76,79,
∴甲、乙的中位数之和为155,故①正确;
78,
81,
[(63﹣78)2+(72﹣78)2+(76﹣78)2+(83﹣78)2+(96﹣78)2]=122.8,
.
故②错误,③正确,④正确,⑤错误.
所以正确的说法是①③④.
故选:B.
3.【解答】解:由t,得x1+x2+…+xn+t=t(n+1),
所以x1+x2+…+xn=tn,所以t,
故两组数据的平均数都是t,
则[(t﹣t)2],
[],
∵,∴,
故选:C.
4.【解答】解:由频率分布直方图可得(0.003+0.007+0.012+2a+0.03+0.008)×10=1,
解得a=0.020.
故选:B.
5.【解答】解:由题意,根据条形图,可得甲户教育支出占,
由饼形图,可得乙户教育支出占25%.可得25%>20%.
所以乙户全年总支出的百分比比甲户全年总支出的百分比大.
故选:B.
6.【解答】解:由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×(39.6%+17%)=31.696%>30%,
互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上,故A正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%>20%,
互联网行业中从事技术岗位的人数超过总人数的20%,故B正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
17%×56%=9.52%>3%,
互联网行业中从事运营岗位的人数90后比80前多,故C正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%<41%,
互联网行业中从事技术岗位的人数90后不一定比80后多,故D错误.
故选:D.
7.【解答】解:由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×(39.6%+17%)=31.696%>30%,
互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上,故①正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%>20%,
互联网行业中从事技术岗位的人数超过总人数的20%,故②正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
17%×56%=9.52%>3%,
互联网行业中从事运营岗位的人数90后比80前多,故③正确;
由整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图得到:
56%×39.6%=22.176%<41%,
互联网行业中从事技术岗位的人数90后不一定比80后多,故④错误.
故正确结论的编号是①②③.
故选:A.
二.填空题
8.【解答】解:由茎叶图知,甲同学的平均成绩与乙同学的众数相等,
即(73+79+82+85+80+m+83+92+93)=84,
解得m=5.
故答案为:5.
9.【解答】解:由频率分布直方图得成绩在[80,90)的频率为:
1﹣(0.01+0.03+0.03+0.01)×10=0.2.
解得x=0.02,
∴这50名学员的平均成绩为:
(55×0.01+65×0.03+75×0.03+85×0.02+95×0.01)×10=74(分).
故答案为:74.
10.【解答】解:该小区居民“抖音APP”的平均使用率的估计值:
0.8,
故答案为:0.8.
11.【解答】解:该组数据按从小到大排列为:2.5,2.7,2.9,3.1,3.6,4.8;
所以这组数据的中位数为
(2.9+3.1)=3.0.
故答案为:3.0.
12.【解答】解:由图可知,年龄在25~35岁之间所对应的扇形圆心角为360°﹣70°﹣130°=160°,
所以年龄小于25岁、年龄在25~35岁之间、年龄大于35岁的居民人均消费之比为70°:160°:130°=7:16:13.
设年龄在25~35岁之间的居民人均消费x元,
则,解得x=1600.
则年龄在25~35岁之间的居民人均消费1600元.
故答案为:1600.
13.【解答】解:利用平均数公式可得这组数据的平均数为:
43.75(元).
故答案为:43.75元.
14.【解答】解:由题可知第3组的人数为0.06×5×100=30;第4组的人数为0.04×5×100=20.
现在用分层抽样的方法在第3,4组共50人中选取5人对新规章制度作深入学习,即抽取比例为,
则采用分层抽样在两组中选取的人数分别为3,2,
则选取的2人来自于不同组的概率为,
故答案为:.
15.【解答】解:由图可知,众数为(4.55+4.85)÷2=4.7;
第五组的频率为0.5×0.3=0.15;
从左至右五个小组的频率之比依次是5:7:12:10:6,可得,
第一小组的频率为0.125;
第二小组的频率为;
第三小组的频率为;
所以中位数在第三小组,第三小组矩形面积为0.3,
则第三小组的高为,
设中位数为x,则0.125+0.175+(x﹣4.55)×1=0.5,
解得x=4.75.
故答案为:4.7,4.75
三.解答题
16.【解答】解:(1)支出在[50,60]元的学生的频率为:1﹣(0.01+0.024+0.036)×10=0.3,
所以,n600;
(2)由频率分布直方图可知,平均支出为:25×0.01×10+35×0.024×10+45×0.036×10+55×0.03×10=43.6;
(3)由题意可知[30,40),[40,50)分别有600×0.024×10=144,600×0.036×10=216,故在[30,40)中抽取2人,在[40,50)中抽取3人,
设事件A为:在[30,40),[40,50)中正好各抽取一人,则P(A).
17.【解答】解:(Ⅰ)由频率分布直方图得:
(0.0012+0.0024×2+0.0036+x+0.0060)×50=1,
解得直方图中x=0.0044.
(Ⅱ)(ⅰ)用电量在[100,250)内的频率为:
(0.0036+0.0060+0.0044)×50=0.7,
∴在这些用户中,用电量在区间[100,250)内的居民数为100×0.7=70户.
(ⅱ)用电量在[150,200)内的户数为0.0060×50×100=30(户),
按分层抽样方法,在这些用户中按1:10的比例抽取用户进一步调查,
用电量在[150,200)内的居民数应该抽取:303(户).
18.【解答】解:(1)从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,
应从第3组抽取:63名志愿者,
从第4组抽取:62名志愿者,
从第5组抽取:61名志愿者.
(2)在(1)的条件下,该市决定在该6名志愿者中随机抽取2名志愿者介绍宣传经验,
基本事件总数n15,
第4组志愿者有人被抽中包含的基本事件个数m9,
∴第4组志愿者有人被抽中的概率P.
19.【解答】解:(1)由频率分布直方图得:
(0.004+a+0.022+0.028+0.022+0.018)×10=1,
解得a=0.006.
(2)由频率分布直方图得:
[40,70)的频率为:(0.004+0.006+0.022)×10=0.32,
[70,80)的频率为:0.028×10=0.28,
∴估计评分的中位数为:
7070.64.
平均数为:45×0.004×10+55×0.006×10+65×0.022×10+75×0.028×10+85×0.022×10+95×0.018×10=76.2.
(3)评分在[40,50)的观影者有:0.004×10×50=2人,评分在[50,60)的观影者有0.006×10×50=3人,
从评分在[40,60)的观影者中随机抽取2人,基本事件总数n10,
至少有一人评分在[40,50)包含的基本事件个数m7,
∴至少有一人评分在[40,50)的概率P.
20.【解答】解:(1)由题意可知(0.005+0.030+0.035+a+0.010)×10=1,
解得a=0.020.
(2)抽取的样本中,
成绩不低于80分的学生所占的比例是(a+0.010)×10=(0.020+0.010)×10=0.3,
所以若从高一学生中随机抽取一人,
估计这名学生数学竞赛成绩不低于80分的概率为0.3.
(3)因为(55×0.005+65×0.030+75×0.035+85×0.020+95×0.010)×10=75,
因此估计高一年级学生本次数学竞赛的平均分为75.
21.【解答】解:(Ⅰ)由频率和为1,得a=1﹣0.12﹣0.22﹣0.36﹣0.12=0.18.
(Ⅱ)计算平均数为0.5×0.12+1.5×0.22+2.5×0.36+3.5×0.18+4.5×0.12=2.46(t),
估计全市家庭月均用水量的平均数为2.46t.
22.【解答】解:(1)前两组的概率和为0.02+0.18=0.2,前三组的概率和为0.02+0.18+036=0.56,
所以0.5﹣0.2=0.3,
故中位数为1515.83;
(2)由已知记第五组的频数为50×0.06×1=3,同理第六组的频数为2,
记第五组的学生为a1,a2,a3,第六组的学生为b1,b2,
因为不小于17秒的两组同学进行特训,特训一段时间后有两位同学成绩符合要求,
则样本空间中所有基本事件为Ω={(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}
共10个样本点,
记事件A:两位同学来自同一组,则
A={(a1,a2),(a1,a3),(a2,a3),(b1,b2)}共4个基本事件样本点;
故P(A).
故这两位同学来自同一组的概率为.
23.【解答】解:(1)由题意得,解得k=300;
(2)由题意得,抽取间距d40,
设75对应的编号是m,则145=m+(4﹣1)×40,m=25,
所以75对应的编号是25,
故(75+79+82+73+81)=78,
s2[(75﹣78)2+(79﹣78)2+(82﹣78)2+(73﹣78)2+(81﹣78)2]=12.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
