第二章《统计》2.3 变量间的相关关系(提高练,含解析)—2020-2021学年人教A版必修三同步必刷题
文档属性
| 名称 | 第二章《统计》2.3 变量间的相关关系(提高练,含解析)—2020-2021学年人教A版必修三同步必刷题 |
|
|
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修三同步必刷题提高练
第二章《统计》
2.3
变量间的相关关系
一.选择题
1.(2020秋?湖南期中)已知x,y的取值如表所示,若y与x线性相关,且0.6x,则( )
x
1
2
3
4
5
y
5.5
6
7
7
8
A.4.2
B.4.6
C.4.7
D.4.9
2.(2020秋?河南月考)已知变量y关于变量x的回归方程为,其一组数据如表所示:
x
1
2
3
4
y
e
e3
e4
e6
若,则x=( )
A.5
B.6
C.7
D.8
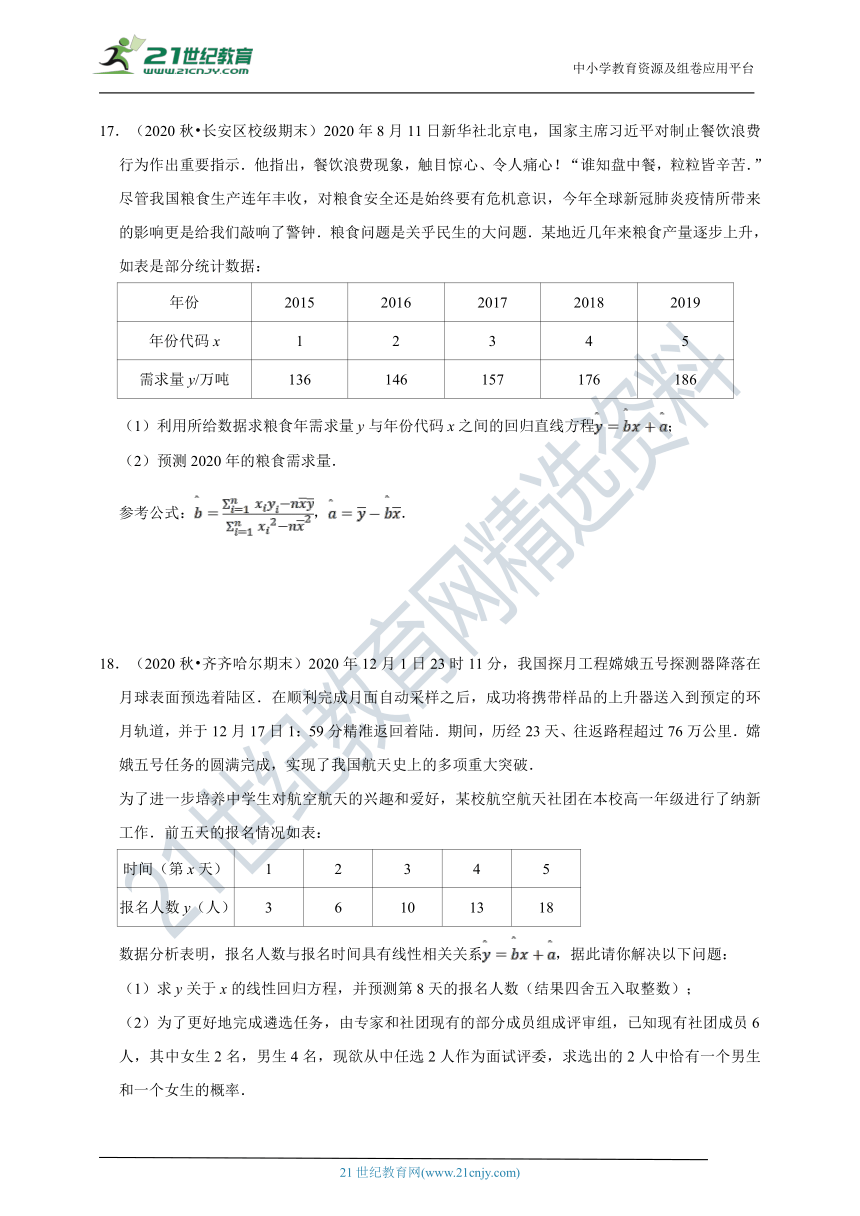
3.(2020秋?垫江县校级月考)某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),图1为选取的15名志愿者身高与臂展的折线图,图2为身高与臂展所对应的散点图,并求得其回归方程为,以下结论中正确的为( )
A.15名志愿者身高的极差大于臂展的极差
B.身高相差10厘米的两人臂展都相差11.6厘米
C.身高为190厘米的人臂展一定为189.65厘米
D.15名志愿者身高和臂展成正相关关系
4.(2020秋?安徽期中)已知x,y的取值如表所示,若y与x线性相关,且回归直线方程为1.46x﹣0.61,则表格中实数m的值为( )
x
2
3
4
5
y
2.2
3.8
5.5
m
A.7.
69
B.7.5
C.6.69
D.6.5
5.(2020?沈阳三模)已知x与y之间的几组数据如表:
x
1
2
3
4
y
1
m
n
4
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为y=b1x+a1,y=b2x+a2,y=b3x+a3,对应的相关系数分别为r1,r2,r3,下列结论中错误的是( )
参考公式:线性回归方程y中,其中,.相关系数r.
A.三条回归直线有共同交点
B.相关系数中,r2最大
C.b1>b2
D.a1>a2
6.(2020?衡阳模拟)某单位为了落实“绿水青山就是金山银山”理念,制定节能减排的目标,先调查了用电量y(单位:度)与气温x(单位:℃)之间的关系,随机选取了4天的用电量与当天气温,并制作了对照表:
x(单位:℃)
17
14
10
﹣1
y(单位:度)
24
34
38
a
由表中数据得线性回归方程:.则a的值为( )
A.48
B.62
C.64
D.68
7.(2019?湖北模拟)为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,得到5组数据:(x1,y1)(x2,y2)(x3,y3),(x4,y4)(x5,y5)根据收集到的数据可知x1+x2+x3+x4+x5=100,由最小二乘法求得回归直线方程为y=0.67x+54.8,则y1+y2+y3+y4+y5的值为( )
A.68.2
B.341
C.355
D.366.2
8.(2018秋?泸州期末)某市为调查某社区居民的家庭收入与年支出的关系,现随机调查了该社区5户家庭,得到如下统计数据:
收入x(万元)
8.5
9
10
11
11.5
支出y(万元)
6.2
7.5
8.0
8.5
9.8
若该社区居民家庭收入与年支出存在线性相关关系,且根据上表得到的回归直线方程是,其中0.76,据此估计,该社区一户年收入为15万元的家庭的年支出约为( )
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元
二.填空题
9.(2020秋?龙岩期中)具有线性相关关系的变量x、y的一组数据如表所示,y与x的回归直线方程为,则b的值为
.
x
0
1
2
3
y
﹣1
1
4
8
10.(2020秋?太和县校级月考)随着我国对新冠肺炎疫情的控制,全国消费市场逐渐回暖,某商场统计的人流量x(单位:百人)与销售额y(单位:万元)的数据表有部分污损,如表所示.
x
2
3
4
5
6
y
2.2
3.8
6.5
7.0
已知x与y具有线性相关关系,且线性回归方程,则表中污损数据应为
.
11.(2020秋?潍坊月考)为了解某社区居民的2019年家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元)
8.2
8.6
10.0
11.3
11.9
支出y(万元)
6.2
7.5
8.0
t
9.8
根据上表可得回归直线方程,则t=
.
12.(2020秋?鼓楼区校级月考)随着新冠肺炎疫情得到控制,消费市场逐渐回暖,某商场统计的客流量x(单位:百人)与销售额y(单位:万元)的数据如表,已知x与y具有线性相关关系,且线性回归方程为1.23x+0.08,则表中的m是
.
x
2
3
4
5
6
y
2.2
3.8
m
6.5
7.0
13.(2018秋?黄冈期末)一个车间为了规定工作原理,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
零件数x(个)
15
20
30
40
50
加工时间y(分钟)
65
70
75
80
90
由表中数据,求得线性回归方程y=0.66x+a,则估计加工70个零件时间为
分钟(精确到0.1).
14.(2018秋?太原期末)如表记录了某公司投入广告费x与销售额y的统计结果,由表可得线性回归方程为yx,据此方程预报当x=6时,y=
x
4
2
3
5
y
49
26
39
54
附:参考公式:,
15.(2019?乐山模拟)为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元)
8.1
8.7
10.1
11.2
11.9
支出y(万元)
6.1
7.6
8.0
8.4
9.9
根据上表可得回归直线方程,,据此估计,该社区一户收入为20万元家庭年支出为
万元.
16.(2018秋?哈尔滨期末)已知x与y之间的一组数据如下,且它们之间存在较好的线性关系.
x
0
2
4
6
y
1
2m+1
2﹣m
3﹣m
则y与x的回归直线方程必过定点
.
三.解答题
17.(2020秋?长安区校级期末)2020年8月11日新华社北京电,国家主席习近平对制止餐饮浪费行为作出重要指示.他指出,餐饮浪费现象,触目惊心、令人痛心!“谁知盘中餐,粒粒皆辛苦.”尽管我国粮食生产连年丰收,对粮食安全还是始终要有危机意识,今年全球新冠肺炎疫情所带来的影响更是给我们敲响了警钟.粮食问题是关乎民生的大问题.某地近几年来粮食产量逐步上升,如表是部分统计数据:
年份
2015
2016
2017
2018
2019
年份代码x
1
2
3
4
5
需求量y/万吨
136
146
157
176
186
(1)利用所给数据求粮食年需求量y与年份代码x之间的回归直线方程;
(2)预测2020年的粮食需求量.
参考公式:,.
18.(2020秋?齐齐哈尔期末)2020年12月1日23时11分,我国探月工程嫦娥五号探测器降落在月球表面预选着陆区.在顺利完成月面自动采样之后,成功将携带样品的上升器送入到预定的环月轨道,并于12月17日1:59分精准返回着陆.期间,历经23天、往返路程超过76万公里.嫦娥五号任务的圆满完成,实现了我国航天史上的多项重大突破.
为了进一步培养中学生对航空航天的兴趣和爱好,某校航空航天社团在本校高一年级进行了纳新工作.前五天的报名情况如表:
时间(第x天)
1
2
3
4
5
报名人数y(人)
3
6
10
13
18
数据分析表明,报名人数与报名时间具有线性相关关系,据此请你解决以下问题:
(1)求y关于x的线性回归方程,并预测第8天的报名人数(结果四舍五入取整数);
(2)为了更好地完成遴选任务,由专家和社团现有的部分成员组成评审组,已知现有社团成员6人,其中女生2名,男生4名,现欲从中任选2人作为面试评委,求选出的2人中恰有一个男生和一个女生的概率.
参考公式:,.
19.(2020秋?香坊区校级期末)2020年初,武汉出现新型冠状病毒肺炎疫情,并快速席卷我国其他地区,口罩成了重要的防疫物资.某口罩生产厂不断加大投入,高速生产,现对其2月1日~2月9日连续9天的日生产量yi(单位:十万只,i=1,2,…,9)数据作了初步处理,得到如图所示的散点图及一些统计量的值:
2.72
19
139.09
1095
注:图中日期代码1~9分别对应2月1日~2月9日;表中zi=e,.
(1)由散点图分析,样本点都集中在曲线y=ln(bt+a)的附近,求y关于t的方程y=ln(bt+a).
(2)估计该厂从什么时候开始日生产量超过四十万只.
参考公式:回归直线方程是vμ,,.
参考数据:e4≈54.6.
20.(2020秋?齐齐哈尔期末)流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春季该园患流感小朋友按照年龄与人数统计,得到如表数据:
年龄(x)
2
3
4
5
6
患病人数(y)
32
32
27
24
20
(1)求y关于x的线性回归方程;
(2)计算变量x、y的相关系数r(计算结果精确到0.01),并回答是否可以认为该幼儿园去年春季患流感人数与年龄相关性很强?
(若|r|∈[0.75,1],则x、y相关性很强;若|r|∈[0.3,0.75),则x、y相关性一般;
若|r|∈[0,0.25],则x、y相关性较弱.)参考数据:.
参考公式:回归方程:,其中,
相关系数:.
21.(2021?十七模拟)中国茶文化博大精深,已知茶水的口感与茶叶类型以及水温有关.经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮用,可以产生最佳口感.某学习研究小组通过测量,得到了下面表格中的数据(室温是20℃).
泡制时间x/min
0
1
2
3
4
水温y/℃
85
79
74
71
65
(1)小组成员根据上面表格中的数据绘制散点图,并根据散点图分布情况,考虑到茶水温度降到室温(即20℃)就不能再降的事实,决定选择函数模型y=kcx+20(x≥0)来刻画.
①令z=ln(y﹣20),求出z关于x的线性回归方程;
②利用①的结论,求出y=kcx+20(x≥0,c>0)中的k与c.
(2)你认为该品种绿茶用85℃的水大约泡制多久后饮用,可以产生最佳口感?
参考数据:ln65≈4.2,ln59≈4.1,ln54≈4.0,ln51≈3.9,ln45≈3.8,log0.90.6≈4.8,e﹣0.1≈0.9,e4.2≈66.7,0.6.
参考公式:x,,.
22.(2021?十八模拟)中国茶文化博大精深,茶水的口感与茶叶类型以及水温有关.经验表明,若某种绿茶用85℃的水泡制,等到茶水温度降至60℃时饮用,则口感最佳.某研究小组通过测量(室温恒为20℃),到下面的表格及散点图:
泡制时间x/min
0
1
2
3
4
水温y/℃
85
79
74
71
65
(1)小组成员根据散点图并考虑茶水温度降到室温(即20℃)就不能再降的事实,决定选择函数模型y=kcx+20(x≥0)来表示x和y的关系.
①令z=ln(y﹣20),求出z关于x的线性回归方程;
②利用①的结论,求出y=kcx+20(x≥0)中的k与c的值.
(2)你认为该品种绿茶用85℃的水泡制多久后饮用,口感最佳?
参考数据:ln65≈4.2,ln59≈4.1,ln54≈4.0,ln51≈3.9,ln45≈3.8,log0.90.6≈4.8,e﹣0.1≈0.9,e4.2≈66.7,0.6.
参考公式:线性回归方程x中,,.
23.(2020秋?城关区校级期末)某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1:
年份x
2015
2016
2017
2018
2019
储蓄存款y(千亿元)
5
6
7
8
10
表1
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x﹣2014,z=y﹣5得到如表2:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
表2
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出得关于x的回归方程;
(Ⅲ)用所求回归方程预测到2022年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程x,其中,.)
24.(2020秋?二道区校级期末)某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
(注:b,a.
参考答案与试题解析
一.选择题
1.【解答】解:由表中数据可知,3,
6.7,
因为样本中心点(3,6.7)在线性回归方程上,所以6.7=0.6×3,
所以4.9.
故选:D.
2.【解答】解:把两边同取对数,得到lnbx﹣0.5,
设bx﹣0.5,得:
x
1
2
3
4
z
1
3
4
6
,,
由,得3.5=2.5b﹣0.5,∴b=1.6,
则1.6x﹣0.5,即e1.6x﹣0.5,
取,得e1.6x﹣0.5=e9.1,即x=6.
故选:B.
3.【解答】解:由图1可知,身高的最大值略小于臂展的最大值,身高的最小值大于臂展的最小值,
则身高极差小于臂展的极差,故A错误;
由回归方程为,
可知身高相差10厘米的两人展臂的估计值相差11.6厘米,不是准确值,故B错误;
把身高190厘米,代入回归方程可得展臂大约为189.65厘米,不是准确值,故C错误;
由相关系数0,可知15名志愿者身高和臂展成正相关关系,故D正确.
故选:D.
4.【解答】解:由题意可得:,,
因为回归直线经过样本中心,1.460.61,
解得m=6.5.
故选:D.
5.【解答】解:由题意,1+m+n+4=10,即m+n=5.
若m=1.5,则n=3.5,此时,.
(1﹣2.5)(1﹣2.5)+(2﹣2.5)(1.5﹣2.5)
+(3﹣2.5)(3.5﹣2.5)+(4﹣2.5)(4﹣2.5)=5.5,
(﹣1.5)2+(﹣0.5)2+0.52+1.52=5,
(﹣1.5)2+(﹣1)2+12+1.52=6.5.
则,a1=2.5﹣1.1×2.5=﹣0.25,;
若m=2,则n=3,此时,.
(1﹣2.5)(1﹣2.5)+(2﹣2.5)(2﹣2.5)+(3﹣2.5)(3﹣2.5)+(4﹣2.5)(4﹣2.5)=5,
5,(﹣1.5)2+(﹣0.5)2+0.52+1.52=5.
,a2=2.5﹣1×2.5=0,;
若m=2.5,则n=2.5,此时,.
(1﹣2.5)(1﹣2.5)+(2﹣2.5)(2.5﹣2.5)
+(3﹣2.5)(2.5﹣2.5)+(4﹣2.5)(4﹣2.5)=4.5,
5,(﹣1.5)2+1.52=4.5,.
由样本点的中心相同,故A正确;
由以上计算可得,相关系数中,r2最大,b1>b2,a1<a2,故B,C正确,D错误.
故选:D.
6.【解答】解:10,24,又回归直线y=﹣2x+60过(,),
∴242×10+60,解得a=64,
故选:C.
7.【解答】解:依题意可得:20,又样本中心点(,)在回归直线y=0.67x+54.8上可得0.67×20+54.8=68.2,
故y1+y2+y3+y4+y5=55×68.2=341,
故选:B.
8.【解答】解:10,8,
再根据样本中心点(,)在回归直线上,所以8=0.76×10可得0.4,
所以线性回归直线方程为0.76x+0.4,
当x=15时,y=0.76×15+0.4,解得y=11.8元.
故选:B.
二.填空题
9.【解答】解:1.5,3,
∴样本点的中心为(1.5,3),
代入,得31.5﹣1.5,解得3.
故答案为:3.
10.【解答】解:设表中污损数据为a,
∵4,
,
∴这组数据的样本中心点是(4,),
∵回归方程,
把样本中心点代入得,1.23×4+0.08,
可得a=5.5.
故答案为:5.5.
11.【解答】解:10..
∴样本点的中心的坐标为(10,).
代入y=0.76x+0.4,得0.76×10+0.4
解得:t=8.5.
故答案为:8.5.
12.【解答】解:由题意,4,,
∵线性回归方程为1.23x+0.08,
根据线性回归方程必过样本的中心,
∴1.23×4+0.08,
∴m=5.5.
故答案为:5.5.
13.【解答】解:31,76,
∴76=0.66×31,解得55.54,
∴0.66x+55.54,
∴x=70时,y=101.7,
故答案为:101.7.
14.【解答】解:根据表中数据,计算(4+2+3+5)=3.5,(49+26+39+54)=42;…(2分)
(xi)(yi)=(4﹣3.5)(49﹣42)+(2﹣3.5)(26﹣42)+(3﹣3.5)(39﹣42)+(5﹣3.5)(54﹣42)=47;
(xi)2=(4﹣3.5)2+(2﹣3.5)2+(3﹣3.5)2+(5﹣3.5)2=5;…(4分)
∴9.4,42﹣9.4×3.5=9.1;…(6分)
所以y关于x的线性回归方程为9.4x+9.1;…(8分)
当x=6时,y=9.4×6+9.1=65.5万元;
由此预测广告费用为7万元时销售额为65.5万元,
故答案为:65.5…(12分)
15.【解答】解:由已知得10,8,
故8﹣0.76×10=0.4,所以回归直线方程为:0.76x+0.4,
令x=20,解得0.76×20+0.4=15.6.
故答案为:15.6.
16.【解答】解:根据题意得,回归直线过样本中心点
∵3,
∴y与x的回归直线方程必过定点(3,)
故答案为(3,).
三.解答题
17.【解答】解:(1)计算样本平均数:3,160.2,
1×136+2×146+3×157+4×176+5×186=2533,
12+22+32+42+52=55,
则13,
160.2﹣13×3=121.2.
故y关于x的线性回归方程为,
(2)将2020年的年份代码x=6代入回归直线方程,
可预测2020年的粮食需求量为:13×6+121.2=199.2.
故预测2020年的粮食需求量199.2万吨.
18.【解答】解:(1)由题意,计算(1+2+3+4+5)=3,
(2+6+10+13+18)=10,
所以3.7,
10﹣3.7×3=﹣1.1,
所以y关于x的线性回归方程为3.7x﹣1.1,
计算x=8时,3.7×8﹣1.1=28.5≈29,
即可预测第8天的报名人数约为29人;
(2)设社团成员6人中女生2名为A、B,男生4名为c、d、e、f,
现从中任选2人,基本事件为AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种,
选出的2人中恰有一个男生和一个女生的基本事件是Ac、Ad、Ae、Af、Bc、Bd、Be、Bf共8种,
故所求的概率值为P.
19.【解答】解:(1)由题意知,y=ln(bt+a),
所以z=ey=bt+a,
计算(1+2+3+4+5+6+7+8+9)=5,
12+22+32+42+52+62+72+82+92=285,
所以4,
19﹣4×5=﹣1,
所以y关于t的方程为y=ln(4t﹣1).
(2)令ln(4t﹣1)>4,解得t13.9,即t≥14,
所以估计该厂从2月14日开始日生产量超过四十万只.
20.【解答】解:(1)由题意得,计算(2+3+4+5+6)=4,
(32+32+27+24+20)=27,
则3.2,
27+3.2×4=39.8,
所以y关于x的线性回归方程为3.2x+39.8.
(2)计算相关系数0.97,
|r|=0.97∈[0.75,1],这说明x、y的相关性很强.
因此可以认为该幼儿园去年春季患流感的人数与年龄相关性很强.
21.【解答】解:(1)①由已知得出x与z的关系,如下表:
泡制时间x/min
0
1
2
3
4
z
4.2
4.1
4.0
3.9
3.8
设线性回归方程,
由题意,得,,
∴(﹣2)×0.2+(﹣1)×0.1+1×(﹣0.1)+2×(﹣0.2)=﹣1,
,
则,
,
则z关于x的线性回归方程为;
②由y=kcx+20(x≥0),得y﹣20=kcx(x≥0),
两边取对数得,ln(y﹣20)=lnk+xlnc,
利用①的结论得:lnc=﹣0.1,lnk=4.2,
∴c=e﹣0.1≈0.9,k=e4.2≈66.7;
(2)由(1)得,y=66.7×0.9x+20(x≥0),
令y=60,得x≈log0.90.6≈4.8.
∴该品种绿茶用85℃的水泡制4.8min后饮用,口感最佳.
22.【解答】解:(1)①由已知得出x与z的关系,如下表:
泡制时间x/min
0
1
2
3
4
z
4.2
4.1
4.0
3.9
3.8
设线性回归方程,
由题意,得,,
∴(﹣2)×0.2+(﹣1)×0.1+1×(﹣0.1)+2×(﹣0.2)=﹣1,
,
则,
,
则z关于x的线性回归方程为;
②由y=kcx+20(x≥0),得y﹣20=kcx(x≥0),
两边取对数得,ln(y﹣20)=lnk+xlnc,
利用①的结论得:lnc=﹣0.1,lnk=4.2,
∴c=e﹣0.1≈0.9,k=e4.2≈66.7;
(2)由(1)得,y=66.7×0.9x+20(x≥0),
令y=60,得x≈log0.90.6≈4.8.
∴该品种绿茶用85℃的水泡制4.8min后饮用,口感最佳.
23.【解答】解:(Ⅰ)3,2.2,45,55,
1.2,
2.2﹣3×1.2=﹣1.4,
所以1.2t﹣1.4.
(Ⅱ)将t=x﹣2014,z=y﹣5,代入1.2t﹣1.4,
得5=1.2(x﹣2014)﹣1.4,即1.2x﹣2413.2.
(Ⅲ)因为1.2×2022﹣2413.2=13.2,
所以预测到2022年底,该地储蓄额可达13.2千亿元.
24.【解答】解:(1)根据表中所列数据可得散点图如图:
(2)5,50,145,13500,xiyi=1380,
∴b6.5,a=50﹣6.5×5=17.5,
∴y=6.5x+17.5;
(3)x=10时,y=6.5×10+17.5=82.5(百万元).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修三同步必刷题提高练
第二章《统计》
2.3
变量间的相关关系
一.选择题
1.(2020秋?湖南期中)已知x,y的取值如表所示,若y与x线性相关,且0.6x,则( )
x
1
2
3
4
5
y
5.5
6
7
7
8
A.4.2
B.4.6
C.4.7
D.4.9
2.(2020秋?河南月考)已知变量y关于变量x的回归方程为,其一组数据如表所示:
x
1
2
3
4
y
e
e3
e4
e6
若,则x=( )
A.5
B.6
C.7
D.8
3.(2020秋?垫江县校级月考)某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),图1为选取的15名志愿者身高与臂展的折线图,图2为身高与臂展所对应的散点图,并求得其回归方程为,以下结论中正确的为( )
A.15名志愿者身高的极差大于臂展的极差
B.身高相差10厘米的两人臂展都相差11.6厘米
C.身高为190厘米的人臂展一定为189.65厘米
D.15名志愿者身高和臂展成正相关关系
4.(2020秋?安徽期中)已知x,y的取值如表所示,若y与x线性相关,且回归直线方程为1.46x﹣0.61,则表格中实数m的值为( )
x
2
3
4
5
y
2.2
3.8
5.5
m
A.7.
69
B.7.5
C.6.69
D.6.5
5.(2020?沈阳三模)已知x与y之间的几组数据如表:
x
1
2
3
4
y
1
m
n
4
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为y=b1x+a1,y=b2x+a2,y=b3x+a3,对应的相关系数分别为r1,r2,r3,下列结论中错误的是( )
参考公式:线性回归方程y中,其中,.相关系数r.
A.三条回归直线有共同交点
B.相关系数中,r2最大
C.b1>b2
D.a1>a2
6.(2020?衡阳模拟)某单位为了落实“绿水青山就是金山银山”理念,制定节能减排的目标,先调查了用电量y(单位:度)与气温x(单位:℃)之间的关系,随机选取了4天的用电量与当天气温,并制作了对照表:
x(单位:℃)
17
14
10
﹣1
y(单位:度)
24
34
38
a
由表中数据得线性回归方程:.则a的值为( )
A.48
B.62
C.64
D.68
7.(2019?湖北模拟)为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,得到5组数据:(x1,y1)(x2,y2)(x3,y3),(x4,y4)(x5,y5)根据收集到的数据可知x1+x2+x3+x4+x5=100,由最小二乘法求得回归直线方程为y=0.67x+54.8,则y1+y2+y3+y4+y5的值为( )
A.68.2
B.341
C.355
D.366.2
8.(2018秋?泸州期末)某市为调查某社区居民的家庭收入与年支出的关系,现随机调查了该社区5户家庭,得到如下统计数据:
收入x(万元)
8.5
9
10
11
11.5
支出y(万元)
6.2
7.5
8.0
8.5
9.8
若该社区居民家庭收入与年支出存在线性相关关系,且根据上表得到的回归直线方程是,其中0.76,据此估计,该社区一户年收入为15万元的家庭的年支出约为( )
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元
二.填空题
9.(2020秋?龙岩期中)具有线性相关关系的变量x、y的一组数据如表所示,y与x的回归直线方程为,则b的值为
.
x
0
1
2
3
y
﹣1
1
4
8
10.(2020秋?太和县校级月考)随着我国对新冠肺炎疫情的控制,全国消费市场逐渐回暖,某商场统计的人流量x(单位:百人)与销售额y(单位:万元)的数据表有部分污损,如表所示.
x
2
3
4
5
6
y
2.2
3.8
6.5
7.0
已知x与y具有线性相关关系,且线性回归方程,则表中污损数据应为
.
11.(2020秋?潍坊月考)为了解某社区居民的2019年家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元)
8.2
8.6
10.0
11.3
11.9
支出y(万元)
6.2
7.5
8.0
t
9.8
根据上表可得回归直线方程,则t=
.
12.(2020秋?鼓楼区校级月考)随着新冠肺炎疫情得到控制,消费市场逐渐回暖,某商场统计的客流量x(单位:百人)与销售额y(单位:万元)的数据如表,已知x与y具有线性相关关系,且线性回归方程为1.23x+0.08,则表中的m是
.
x
2
3
4
5
6
y
2.2
3.8
m
6.5
7.0
13.(2018秋?黄冈期末)一个车间为了规定工作原理,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
零件数x(个)
15
20
30
40
50
加工时间y(分钟)
65
70
75
80
90
由表中数据,求得线性回归方程y=0.66x+a,则估计加工70个零件时间为
分钟(精确到0.1).
14.(2018秋?太原期末)如表记录了某公司投入广告费x与销售额y的统计结果,由表可得线性回归方程为yx,据此方程预报当x=6时,y=
x
4
2
3
5
y
49
26
39
54
附:参考公式:,
15.(2019?乐山模拟)为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元)
8.1
8.7
10.1
11.2
11.9
支出y(万元)
6.1
7.6
8.0
8.4
9.9
根据上表可得回归直线方程,,据此估计,该社区一户收入为20万元家庭年支出为
万元.
16.(2018秋?哈尔滨期末)已知x与y之间的一组数据如下,且它们之间存在较好的线性关系.
x
0
2
4
6
y
1
2m+1
2﹣m
3﹣m
则y与x的回归直线方程必过定点
.
三.解答题
17.(2020秋?长安区校级期末)2020年8月11日新华社北京电,国家主席习近平对制止餐饮浪费行为作出重要指示.他指出,餐饮浪费现象,触目惊心、令人痛心!“谁知盘中餐,粒粒皆辛苦.”尽管我国粮食生产连年丰收,对粮食安全还是始终要有危机意识,今年全球新冠肺炎疫情所带来的影响更是给我们敲响了警钟.粮食问题是关乎民生的大问题.某地近几年来粮食产量逐步上升,如表是部分统计数据:
年份
2015
2016
2017
2018
2019
年份代码x
1
2
3
4
5
需求量y/万吨
136
146
157
176
186
(1)利用所给数据求粮食年需求量y与年份代码x之间的回归直线方程;
(2)预测2020年的粮食需求量.
参考公式:,.
18.(2020秋?齐齐哈尔期末)2020年12月1日23时11分,我国探月工程嫦娥五号探测器降落在月球表面预选着陆区.在顺利完成月面自动采样之后,成功将携带样品的上升器送入到预定的环月轨道,并于12月17日1:59分精准返回着陆.期间,历经23天、往返路程超过76万公里.嫦娥五号任务的圆满完成,实现了我国航天史上的多项重大突破.
为了进一步培养中学生对航空航天的兴趣和爱好,某校航空航天社团在本校高一年级进行了纳新工作.前五天的报名情况如表:
时间(第x天)
1
2
3
4
5
报名人数y(人)
3
6
10
13
18
数据分析表明,报名人数与报名时间具有线性相关关系,据此请你解决以下问题:
(1)求y关于x的线性回归方程,并预测第8天的报名人数(结果四舍五入取整数);
(2)为了更好地完成遴选任务,由专家和社团现有的部分成员组成评审组,已知现有社团成员6人,其中女生2名,男生4名,现欲从中任选2人作为面试评委,求选出的2人中恰有一个男生和一个女生的概率.
参考公式:,.
19.(2020秋?香坊区校级期末)2020年初,武汉出现新型冠状病毒肺炎疫情,并快速席卷我国其他地区,口罩成了重要的防疫物资.某口罩生产厂不断加大投入,高速生产,现对其2月1日~2月9日连续9天的日生产量yi(单位:十万只,i=1,2,…,9)数据作了初步处理,得到如图所示的散点图及一些统计量的值:
2.72
19
139.09
1095
注:图中日期代码1~9分别对应2月1日~2月9日;表中zi=e,.
(1)由散点图分析,样本点都集中在曲线y=ln(bt+a)的附近,求y关于t的方程y=ln(bt+a).
(2)估计该厂从什么时候开始日生产量超过四十万只.
参考公式:回归直线方程是vμ,,.
参考数据:e4≈54.6.
20.(2020秋?齐齐哈尔期末)流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春季该园患流感小朋友按照年龄与人数统计,得到如表数据:
年龄(x)
2
3
4
5
6
患病人数(y)
32
32
27
24
20
(1)求y关于x的线性回归方程;
(2)计算变量x、y的相关系数r(计算结果精确到0.01),并回答是否可以认为该幼儿园去年春季患流感人数与年龄相关性很强?
(若|r|∈[0.75,1],则x、y相关性很强;若|r|∈[0.3,0.75),则x、y相关性一般;
若|r|∈[0,0.25],则x、y相关性较弱.)参考数据:.
参考公式:回归方程:,其中,
相关系数:.
21.(2021?十七模拟)中国茶文化博大精深,已知茶水的口感与茶叶类型以及水温有关.经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮用,可以产生最佳口感.某学习研究小组通过测量,得到了下面表格中的数据(室温是20℃).
泡制时间x/min
0
1
2
3
4
水温y/℃
85
79
74
71
65
(1)小组成员根据上面表格中的数据绘制散点图,并根据散点图分布情况,考虑到茶水温度降到室温(即20℃)就不能再降的事实,决定选择函数模型y=kcx+20(x≥0)来刻画.
①令z=ln(y﹣20),求出z关于x的线性回归方程;
②利用①的结论,求出y=kcx+20(x≥0,c>0)中的k与c.
(2)你认为该品种绿茶用85℃的水大约泡制多久后饮用,可以产生最佳口感?
参考数据:ln65≈4.2,ln59≈4.1,ln54≈4.0,ln51≈3.9,ln45≈3.8,log0.90.6≈4.8,e﹣0.1≈0.9,e4.2≈66.7,0.6.
参考公式:x,,.
22.(2021?十八模拟)中国茶文化博大精深,茶水的口感与茶叶类型以及水温有关.经验表明,若某种绿茶用85℃的水泡制,等到茶水温度降至60℃时饮用,则口感最佳.某研究小组通过测量(室温恒为20℃),到下面的表格及散点图:
泡制时间x/min
0
1
2
3
4
水温y/℃
85
79
74
71
65
(1)小组成员根据散点图并考虑茶水温度降到室温(即20℃)就不能再降的事实,决定选择函数模型y=kcx+20(x≥0)来表示x和y的关系.
①令z=ln(y﹣20),求出z关于x的线性回归方程;
②利用①的结论,求出y=kcx+20(x≥0)中的k与c的值.
(2)你认为该品种绿茶用85℃的水泡制多久后饮用,口感最佳?
参考数据:ln65≈4.2,ln59≈4.1,ln54≈4.0,ln51≈3.9,ln45≈3.8,log0.90.6≈4.8,e﹣0.1≈0.9,e4.2≈66.7,0.6.
参考公式:线性回归方程x中,,.
23.(2020秋?城关区校级期末)某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1:
年份x
2015
2016
2017
2018
2019
储蓄存款y(千亿元)
5
6
7
8
10
表1
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x﹣2014,z=y﹣5得到如表2:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
表2
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出得关于x的回归方程;
(Ⅲ)用所求回归方程预测到2022年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程x,其中,.)
24.(2020秋?二道区校级期末)某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
(注:b,a.
参考答案与试题解析
一.选择题
1.【解答】解:由表中数据可知,3,
6.7,
因为样本中心点(3,6.7)在线性回归方程上,所以6.7=0.6×3,
所以4.9.
故选:D.
2.【解答】解:把两边同取对数,得到lnbx﹣0.5,
设bx﹣0.5,得:
x
1
2
3
4
z
1
3
4
6
,,
由,得3.5=2.5b﹣0.5,∴b=1.6,
则1.6x﹣0.5,即e1.6x﹣0.5,
取,得e1.6x﹣0.5=e9.1,即x=6.
故选:B.
3.【解答】解:由图1可知,身高的最大值略小于臂展的最大值,身高的最小值大于臂展的最小值,
则身高极差小于臂展的极差,故A错误;
由回归方程为,
可知身高相差10厘米的两人展臂的估计值相差11.6厘米,不是准确值,故B错误;
把身高190厘米,代入回归方程可得展臂大约为189.65厘米,不是准确值,故C错误;
由相关系数0,可知15名志愿者身高和臂展成正相关关系,故D正确.
故选:D.
4.【解答】解:由题意可得:,,
因为回归直线经过样本中心,1.460.61,
解得m=6.5.
故选:D.
5.【解答】解:由题意,1+m+n+4=10,即m+n=5.
若m=1.5,则n=3.5,此时,.
(1﹣2.5)(1﹣2.5)+(2﹣2.5)(1.5﹣2.5)
+(3﹣2.5)(3.5﹣2.5)+(4﹣2.5)(4﹣2.5)=5.5,
(﹣1.5)2+(﹣0.5)2+0.52+1.52=5,
(﹣1.5)2+(﹣1)2+12+1.52=6.5.
则,a1=2.5﹣1.1×2.5=﹣0.25,;
若m=2,则n=3,此时,.
(1﹣2.5)(1﹣2.5)+(2﹣2.5)(2﹣2.5)+(3﹣2.5)(3﹣2.5)+(4﹣2.5)(4﹣2.5)=5,
5,(﹣1.5)2+(﹣0.5)2+0.52+1.52=5.
,a2=2.5﹣1×2.5=0,;
若m=2.5,则n=2.5,此时,.
(1﹣2.5)(1﹣2.5)+(2﹣2.5)(2.5﹣2.5)
+(3﹣2.5)(2.5﹣2.5)+(4﹣2.5)(4﹣2.5)=4.5,
5,(﹣1.5)2+1.52=4.5,.
由样本点的中心相同,故A正确;
由以上计算可得,相关系数中,r2最大,b1>b2,a1<a2,故B,C正确,D错误.
故选:D.
6.【解答】解:10,24,又回归直线y=﹣2x+60过(,),
∴242×10+60,解得a=64,
故选:C.
7.【解答】解:依题意可得:20,又样本中心点(,)在回归直线y=0.67x+54.8上可得0.67×20+54.8=68.2,
故y1+y2+y3+y4+y5=55×68.2=341,
故选:B.
8.【解答】解:10,8,
再根据样本中心点(,)在回归直线上,所以8=0.76×10可得0.4,
所以线性回归直线方程为0.76x+0.4,
当x=15时,y=0.76×15+0.4,解得y=11.8元.
故选:B.
二.填空题
9.【解答】解:1.5,3,
∴样本点的中心为(1.5,3),
代入,得31.5﹣1.5,解得3.
故答案为:3.
10.【解答】解:设表中污损数据为a,
∵4,
,
∴这组数据的样本中心点是(4,),
∵回归方程,
把样本中心点代入得,1.23×4+0.08,
可得a=5.5.
故答案为:5.5.
11.【解答】解:10..
∴样本点的中心的坐标为(10,).
代入y=0.76x+0.4,得0.76×10+0.4
解得:t=8.5.
故答案为:8.5.
12.【解答】解:由题意,4,,
∵线性回归方程为1.23x+0.08,
根据线性回归方程必过样本的中心,
∴1.23×4+0.08,
∴m=5.5.
故答案为:5.5.
13.【解答】解:31,76,
∴76=0.66×31,解得55.54,
∴0.66x+55.54,
∴x=70时,y=101.7,
故答案为:101.7.
14.【解答】解:根据表中数据,计算(4+2+3+5)=3.5,(49+26+39+54)=42;…(2分)
(xi)(yi)=(4﹣3.5)(49﹣42)+(2﹣3.5)(26﹣42)+(3﹣3.5)(39﹣42)+(5﹣3.5)(54﹣42)=47;
(xi)2=(4﹣3.5)2+(2﹣3.5)2+(3﹣3.5)2+(5﹣3.5)2=5;…(4分)
∴9.4,42﹣9.4×3.5=9.1;…(6分)
所以y关于x的线性回归方程为9.4x+9.1;…(8分)
当x=6时,y=9.4×6+9.1=65.5万元;
由此预测广告费用为7万元时销售额为65.5万元,
故答案为:65.5…(12分)
15.【解答】解:由已知得10,8,
故8﹣0.76×10=0.4,所以回归直线方程为:0.76x+0.4,
令x=20,解得0.76×20+0.4=15.6.
故答案为:15.6.
16.【解答】解:根据题意得,回归直线过样本中心点
∵3,
∴y与x的回归直线方程必过定点(3,)
故答案为(3,).
三.解答题
17.【解答】解:(1)计算样本平均数:3,160.2,
1×136+2×146+3×157+4×176+5×186=2533,
12+22+32+42+52=55,
则13,
160.2﹣13×3=121.2.
故y关于x的线性回归方程为,
(2)将2020年的年份代码x=6代入回归直线方程,
可预测2020年的粮食需求量为:13×6+121.2=199.2.
故预测2020年的粮食需求量199.2万吨.
18.【解答】解:(1)由题意,计算(1+2+3+4+5)=3,
(2+6+10+13+18)=10,
所以3.7,
10﹣3.7×3=﹣1.1,
所以y关于x的线性回归方程为3.7x﹣1.1,
计算x=8时,3.7×8﹣1.1=28.5≈29,
即可预测第8天的报名人数约为29人;
(2)设社团成员6人中女生2名为A、B,男生4名为c、d、e、f,
现从中任选2人,基本事件为AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种,
选出的2人中恰有一个男生和一个女生的基本事件是Ac、Ad、Ae、Af、Bc、Bd、Be、Bf共8种,
故所求的概率值为P.
19.【解答】解:(1)由题意知,y=ln(bt+a),
所以z=ey=bt+a,
计算(1+2+3+4+5+6+7+8+9)=5,
12+22+32+42+52+62+72+82+92=285,
所以4,
19﹣4×5=﹣1,
所以y关于t的方程为y=ln(4t﹣1).
(2)令ln(4t﹣1)>4,解得t13.9,即t≥14,
所以估计该厂从2月14日开始日生产量超过四十万只.
20.【解答】解:(1)由题意得,计算(2+3+4+5+6)=4,
(32+32+27+24+20)=27,
则3.2,
27+3.2×4=39.8,
所以y关于x的线性回归方程为3.2x+39.8.
(2)计算相关系数0.97,
|r|=0.97∈[0.75,1],这说明x、y的相关性很强.
因此可以认为该幼儿园去年春季患流感的人数与年龄相关性很强.
21.【解答】解:(1)①由已知得出x与z的关系,如下表:
泡制时间x/min
0
1
2
3
4
z
4.2
4.1
4.0
3.9
3.8
设线性回归方程,
由题意,得,,
∴(﹣2)×0.2+(﹣1)×0.1+1×(﹣0.1)+2×(﹣0.2)=﹣1,
,
则,
,
则z关于x的线性回归方程为;
②由y=kcx+20(x≥0),得y﹣20=kcx(x≥0),
两边取对数得,ln(y﹣20)=lnk+xlnc,
利用①的结论得:lnc=﹣0.1,lnk=4.2,
∴c=e﹣0.1≈0.9,k=e4.2≈66.7;
(2)由(1)得,y=66.7×0.9x+20(x≥0),
令y=60,得x≈log0.90.6≈4.8.
∴该品种绿茶用85℃的水泡制4.8min后饮用,口感最佳.
22.【解答】解:(1)①由已知得出x与z的关系,如下表:
泡制时间x/min
0
1
2
3
4
z
4.2
4.1
4.0
3.9
3.8
设线性回归方程,
由题意,得,,
∴(﹣2)×0.2+(﹣1)×0.1+1×(﹣0.1)+2×(﹣0.2)=﹣1,
,
则,
,
则z关于x的线性回归方程为;
②由y=kcx+20(x≥0),得y﹣20=kcx(x≥0),
两边取对数得,ln(y﹣20)=lnk+xlnc,
利用①的结论得:lnc=﹣0.1,lnk=4.2,
∴c=e﹣0.1≈0.9,k=e4.2≈66.7;
(2)由(1)得,y=66.7×0.9x+20(x≥0),
令y=60,得x≈log0.90.6≈4.8.
∴该品种绿茶用85℃的水泡制4.8min后饮用,口感最佳.
23.【解答】解:(Ⅰ)3,2.2,45,55,
1.2,
2.2﹣3×1.2=﹣1.4,
所以1.2t﹣1.4.
(Ⅱ)将t=x﹣2014,z=y﹣5,代入1.2t﹣1.4,
得5=1.2(x﹣2014)﹣1.4,即1.2x﹣2413.2.
(Ⅲ)因为1.2×2022﹣2413.2=13.2,
所以预测到2022年底,该地储蓄额可达13.2千亿元.
24.【解答】解:(1)根据表中所列数据可得散点图如图:
(2)5,50,145,13500,xiyi=1380,
∴b6.5,a=50﹣6.5×5=17.5,
∴y=6.5x+17.5;
(3)x=10时,y=6.5×10+17.5=82.5(百万元).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
