第三章《概率》3.2 古典概型(提高练,含解析)—2020-2021学年人教A版必修三同步必刷题
文档属性
| 名称 | 第三章《概率》3.2 古典概型(提高练,含解析)—2020-2021学年人教A版必修三同步必刷题 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-13 23:56:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修三同步必刷题提高练
第三章《概率》
3.2
古典概型
一.选择题
1.(2020秋?南关区校级期末)2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款、法国8款、荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国.A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香烃矿物油成分,则随机抽取3袋,恰有2袋含有芳香烃矿物油成分的概率为( )
A.
B.
C.
D.
2.(2020秋?湖北月考)党的十八大要求全面实施素质教育,培养德智体美劳全面发展的社会主义建设者和接班人,劳动教育受到全社会广泛关注.某学校的某班级将5名同学分配到甲、乙、丙三个村参加劳动锻炼,每个村至少分配一位同学,则甲村恰好分配2位同学的概率为( )
A.
B.
C.
D.
3.(2020秋?垫江县校级月考)马林?梅森(MarinMersenne,1588﹣1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物.梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为纪念梅森在数论方面的这一贡献,将形如2p﹣1(其中p是素数)的素数,称为梅森素数.在不超过50的素数中,随机选取两个不同的数,至少有一个为梅森素数的概率是( )
A.
B.
C.
D.
4.(2020秋?建邺区校级月考)若从甲、乙、丙、丁4人中选出3名代表参加学校会议,则甲被选中的概率为( )
A.
B.
C.
D.
5.(2020?Ⅱ卷模拟)《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“─”表示一个阳爻,“﹣﹣”表示一个阴爻).若从含有两个及以上阳爻的卦中任取两卦,这两卦的六个爻中都恰有两个阳爻的概率为( )
A.
B.
C.
D.
6.(2020?青羊区校级模拟)从2名男生和3名女生中任选三人参加比赛,选中1名男生和2名女生的概率为( )
A.
B.
C.
D.
7.(2020?合肥二模)为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着A,B,C三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择A,B,C三个项目的意向如表:
扶贫项目
A
B
C
选择意向贫困户
甲、乙、丙、丁
甲、乙、丙
丙、丁
若每个贫困户只能从自己登记的选择意向中随机选取一项,且每个项目至多有两户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.
B.
C.
D.
8.(2020?梧州模拟)数学与文学有许多奇妙的联系,如诗中有回文诗:“儿忆父兮妻忆夫”,既可以顺读也可以逆读,数学中有回文数,如343、12521等,两位数的回文数有11、22、33、…、99共9个,则三位数的回文数中为偶数的概率是( )
A.
B.
C.
D.
二.填空题
9.(2020秋?历城区校级期中)已知7件产品中有5件合格品,2件次品.为找出这2件次品,每次任取一件检验,检验后不放回,则“恰好第一次检验出正品且第五次检验出最后一件次品”的概率为
.
10.(2020秋?浦东新区校级月考)有五张写有1、2、3、4、5的卡片,每次抽取1张记好数字后放回,这样抽4次,则抽到的最大数与最小数的差小于4的概率是
.
11.(2020?北京自主招生)从0﹣9共10个数中任取5个组成一个5位或4位(0在首位)数,则该数被396整除概率为
.
12.(2020秋?闵行区校级月考)我校5位同学报考了北京大学“强基计划”第I专业组,并顺利通过各项考核,已知5位同学将根据综合成绩和志愿顺序随机地进入教学类、物理学类、力学类这三个专业中的某一个专业,则这三个专业都有我校学生的概率是
(结果用最简分数表示).
13.(2020春?闵行区校级月考)假设一个随机数发生器一次只能从1,2,3,…,9这九个数学中等可能地选一个数,则该随机数发生器完成了n(n>1)次选择后,选出的n个数的乘积能被10整除的概率为
(用含n的代数式示).
14.(2020秋?浙江月考)甲从集合{1,2,3,4,5,6,7,8,9}中任取三个不同的元素,并按降序排列得到十进制三位数a,乙从集合{1,2,3,4,5,6,7,8}中任取三个不同的元素,按降序排列得到十进制三位数b,则a>b的概率为
.
15.(2020?普陀区三模)若实数a、b、c满足═,则a,b,c是调和的.设含有三个元素的集合P是集合M={x||x|≤2020,x∈Z}的子集,当集合P中的元素a、b、c既是等差的又是调和的时,称集合P为“好集”.则三元子集中“好集”的概率是
.
16.(2020春?滨海县校级期末)某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为
.
三.解答题
17.(2021?八模拟)2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗击疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课,每天共240分钟,请学生自主学习.区教育局为了了解学生网上学习情况,上课几天后在全区学生中采取随机抽样的方法抽取了200名学生进行问卷调查,为了方便表述把学习时间在[0,120)分钟的学生称为A类,把学习时间在[120,240]分钟的学生称为B类,调查的200名学生学习时间的人数频率分布表如表:
学习时间
[0,40)
[40,80)
[80,120)
[120,160)
[160,200)
[200,240]
频数
20
35
n
60
10
10
频率
以频率估计概率回答下列问题:
(Ⅰ)求表中n的值并完成上表,并估算这200名学生学习时间的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(Ⅱ)在A,B两类学生中,按分层抽样的方法从上述200名学生中抽取5人,求从这五人中抽取的两人都是A类学生的概率.
18.(2020秋?广西期中)(1)从2,3,8,9中任取两个不同的数字,分别记为a,b,求a+b为奇数的概率;
(2)已知a∈[﹣5,5],关于x的一元二次方程x2﹣ax+4=0,求此方程没有实根的概率.
19.(2020秋?湖北期中)(1)一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射后与y轴交于点H,求反射光线QH所在直线的方程.
(2)已知甲罐中有四个相同的小球,标号为1,2,3,4;乙罐中有五个相同的小球,标号为1,2,3,5,6,现从甲罐、乙罐中分别随机抽取1个小球,记事件A=“抽取的两个小球标号之和大于5”,事件B=“抽取的两个小球标号之积大于8”,求事件“A∪B”发生的概率.
20.(2020秋?聊城期中)某次联欢会上设有一个抽奖游戏抽奖箱中共有16个四种不同颜色且形状大小完全相同的小球,分别代表﹣等奖、二等奖、三等奖、无奖四种奖项.其中红球代表一等奖且只有1个,黄球代表三等奖.从中任取一个小球,若中二等奖或三等奖的概率.小华同学获得一次摸奖机会.
(1)求他不能中奖的概率;
(2)若该同学中一等奖或二等奖的概率是,试计算黄球的个数.
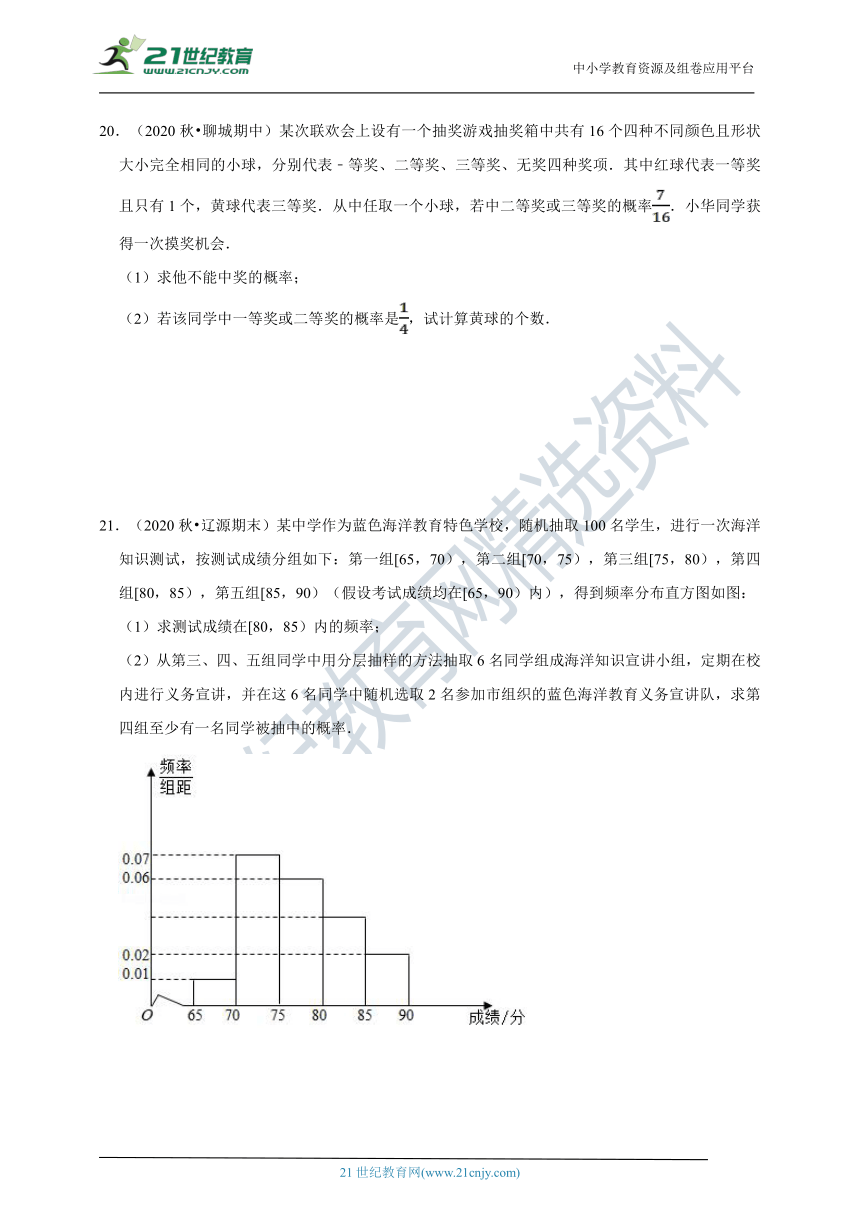
21.(2020秋?辽源期末)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的概率.
22.(2020秋?湖南月考)某质量检测部门为评估工厂某自动化设备生产零件T的性能情况,从该自动化设备生产零件T的流水线上随机抽取100件零件T为样本,测量其直径后,整理得到如表:
直径(单位:mm)
78
79
81
82
83
84
85
件数
1
1
3
5
6
19
33
直径(单位:mm)
86
87
88
89
90
91
93
件数
18
4
4
3
1
1
1
经计算,样本的平均值84.98,标准差s=2.2,用频率值作为概率的估计值.
(1)从该自动化设备加工的零件T中任意抽取一件,记其直径为d,根据下列不等式评估该自动化设备的性能:①P(s<ds)≥0.68;②P(2s<d2s)≥0.95;P(3s<d3s)≥0.99(P表示相应事件的概率).等级评估方法为:若同时满足上述三个式子,则自动化设备等级为A;若仅满足其中两个,自动化设备等级为B;若仅满足其中一个,则自动化设备等级为C;若全部都不满足,则自动化设备等级为D.试评估该自动化设备性能的等级情况;
(2)从样本中直径尺寸在(2x,2s)之外的零件T中随机抽取2件,求至少有1件直径尺寸在(3s,3s)之外的概率.
23.(2020春?通州区期末)为了解学生“课外阅读日”的活动情况,某校以10%的比例对高二年级500名学生按选修物理和选修历史进行分层抽样调查,测得阅读时间(单位:分钟)的频数统计图如图:
(1)分别估计该校高二年级选修物理和选修历史的人数;
(2)估计该校高二年级学生阅读时间在60分钟以上的概率;
(3)从样本中阅读时间在60~90分钟的选修物理的学生中任选2人,求至少有1人阅读时间在75~90之间的概率.
24.(2020春?咸阳期末)某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人5次数学考试的成绩,统计结果如表:
第一次
第二次
第三次
第四次
第五次
甲的成绩(分)
80
85
71
92
87
乙的成绩(分)
90
76
75
92
82
(Ⅰ)已知甲、乙两名学生这5次数学考试成绩的平均分都为83分,若从甲、乙两名学生中选一人参加数学竞赛,请从统计学的角度考虑,你认为选谁参加数学竞赛较合适?并说明理由;
(Ⅱ)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.
已知学生甲、乙都只会5道备选题中的3道,那么你推荐的选手选择哪种答题方案进入复赛的可能性更大?并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:记6袋奶粉中,不含芳香烃矿物油成分的奶粉为A、B,含芳香烃矿物油成分的奶粉为a、b、c、d,
任取3袋,所有的情况为:
(A,B,a),(A,B,b),(A,B,c),(A,B,d),(A,a,b),(A,a,c),(A,a,d),
(A,b,c),(A,b,d),(A,c,d),(B,a,b),(B,a,c),(B,a,d),(B,b,c),
(B,b,d),(B,c,d),(a,b,c),(a,b,d),(a,c,d),(b,c,d),共20种,
其中恰有2袋含有芳香烃矿物油成分包含的基本事件有:
(A,a,b),(A,a,c),(A,a,d),(A,b,c),(A,b,d),(A,c,d),(B,a,b),
(B,a,c),(B,a,d),(B,b,c),(B,b,d),(B,c,d),共12种,
故恰有2袋含有芳香烃矿物油成分的概率为:.
故选:D.
2.【解答】解:某学校的某班级将5名同学分配到甲、乙、丙三个村参加劳动锻炼,
每个村至少分配一位同学,
基本事件总数n150,
其中甲村恰好分配2位同学包含的基本事件个数m60,
∴甲村恰好分配2位同学的概率为P.
故选:B.
3.【解答】解:在不超过50的素数有:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,共15个,
其中梅森素数有:3,7,31,共3个,
在不超过50的素数中,随机选取两个不同的数包含的基本事件个数n105,
至少有一个为梅森素数包的基本事件个数m39.
∴至少有一个为梅森素数的概率P.
故选:B.
4.【解答】解:从甲,乙,丙,丁4位同学中选出3名代表参加学校会议,
基本事件总数n4,
甲被选中包含的基本事件个数m3,
则甲被选中的概率p.
故选:D.
5.【解答】解:含有两个阳爻的卦有3个,含有三个阳爻的卦有1个,
从含有两个及以上阳爻的卦中任取两卦,
基本事件总数n6,
这两卦的六个爻中都恰有两个阳爻包含的基本事件个数m3,
∴这两卦的六个爻中都恰有两个阳爻的概率为p.
故选:B.
6.【解答】解:记2名男生为A1,A2,3名女生为B1,B2,B3,
所有的结果为:A1A2B1,A1A2B2,A1A2B3,A1B1B2,A1B1B3,
A1B2B3,A2B1B2,A2B1B3,A2B2B3,B1B2B3,一共有10种情况,
符合条件的有:A1B1B2,A1B1B3,A1B2B3,
A2B1B2,A2B1B3,A2B2B3,共6种情况,
所以概率为,
故选:C.
7.【解答】解:由题意:甲乙只能选A,B项目,丁只能选A,C项目,丙则都可以.
由题意基本事件可分以下三类:
(1)甲乙都选A,则丁只能选C,丙则可以选B,C任一个,故共有2种方法;
(2)甲乙都选B,则丁可以选A或C,丙也可选A或C,故共有种方法.
(3)甲乙分别选AB之一,然后丁选A时,丙只能选B或C;丁选C时,丙则A,B,C都可以选.故有种方法.
故基本事件共有2+4+10=16种.
甲乙选同一种项目的共有2+4=6种.
故甲乙选同一项目的概率P.
故选:A.
8.【解答】解:三位数的回文数为ABA,
A共有1到9共9种可能,即1B1、2B2、3B3…
B共有0到9共10种可能,即A0A、A1A、A2A、A3A、…
共有9×10=90个,
其中偶数为A是偶数,共4种可能,即2B2,4B4,6B6,8B8,
B共有0到9共10种可能,即A0A、A1A、A2A、A3A、…
其有4×10=40个,
∴三位数的回文数中,偶数的概率P;
故选:D.
二.填空题
9.【解答】解:考查两件次品的位置,共有n21种取法,
因为恰好第五次取出最后一件次品,
依题意另一件次品只能排2,3,4位,共有m3种取法.
故“恰好第一次检验出正品且第五次检验出最后一件次品”的概率为p.
故答案为:.
10.【解答】解:有五张写有1、2、3、4、5的卡片,每次抽取1张记好数字后放回,这样抽4次,
共有54种不同的取法,差值可能为1,2,3,4,
最大数与最小数的差等于4,则4次抽取中5或1没有抽到,
没有抽到1的有44,没有抽到5的有44,5和1都没有抽到的有34,
所以抽到的最大数与最小数的差小于4有2×44﹣34种,
所以抽到的最大数与最小数的差小于4的概率.
故答案为:.
11.【解答】解:396=9×4×11,
先考虑被9整除的组合,
(1,8),(2,7),(3,6),(4,5),任意两组,加上0,9,(1)
(1,2,3,4,8),(1,2,3,5,7),(1,2,4,5,6),(2)
(1,2,6),(1,3,5),(2,3,4),加上0,9,(3)
再考虑被11整除,(1)中只能加0,
最后考虑被4整除,(1,2,3,5,7)舍去,(1,3,5)加上0,9舍去,
(1)中所有情况数为:48,
(2)中所有情况数为:8,
(3)中所有情况数为8,
综上共有:8+8+48=64种情况,
∴该数被396整除概率为P.
故答案为:.
12.【解答】解:5位同学将根据综合成绩和志愿顺序随机地进入教学类、物理学类、力学类这三个专业中的某一个专业,
基本事件总数n=35=243,
这三个专业都有我校学生包含的情况有两种,各个专业的学生数分别为1,1,3和2,2,1,
∴这三个专业都有我校学生包含的基本事件个数m=()?150,
则这三个专业都有我校学生的概率是p.
故答案为:.
13.【解答】解:要便n个数之积平衡车10整除,必须有一个数是5,有一个数是偶数,
n次选择的方法总共有9n种,其中:
A、每一次均不取5的取法,有8n种,
B、每一次均不取偶数的取法,有5n种,
C、每一次均在{1,3,7,9}中取数的方法有4n种,
由题意中C中的取法既包含于A,也包含于B,
∴该随机数发生器完成了n(n>1)次选择后,选出的n个数的乘积能被10整除的概率为:
P=1.
故答案为:1.
14.【解答】解:甲从集合{1,2,3,4,5,6,7,8,9}中任取三个不同的元素,并按降序排列得到十进制三位数a,
共有84种情况,
乙从集合{1,2,3,4,5,6,7,8}中任取三个不同的元素,按降序排列得到十进制三位数b,
共有56种情况,
故三位数a,b进行比较可得到84×56种情况,
乙取到的三位数甲都能取到,若乙取到的数是123,这在甲中是取得的最小的三位数,
则在甲取得的数中,除了123外,其它的数都比123大,共有84﹣1=83种情况,
当乙取得其它数时,分析同理,则可以得到在所有数的比较中,a>b的情况共有:
83+82+81+…+29+28种,
故a>b的概率为,
故答案为:.
15.【解答】解:因为P为三元素集合,
所以实数a,b,c互不相等,且均不为0,
根据题意可得,得2b2﹣ab﹣a2=0,
解得a=b(舍),或a=﹣2b,则c=4b
所以集合P={b,﹣2b,4b},
又因为含有三个元素的集合P是集合M={x||x|≤2020,x∈Z}的子集,
所以﹣2020≤4b≤2020,即﹣505≤b≤505,且b≠0
所以集合P的个数为:2×505=1010,
集合M中共由4041个元素,
所以三元子集中“好集”的概率是,
故答案为:.
16.【解答】解:我们把从顶点A到3的路线图单独画出来:
分析可得,
从顶点A到3总共有C52=10种走法,每一种走法的概率都是,
∴珠子从出口3出来是()5.
三.解答题
17.【解答】解:(Ⅰ)由题知被调查者一共200人,
∴35+60+n+20+10+10=200,解得n=65.
则被调查人员各组学习时间的频率分别为0.1,0.175,0.325,0.3,0.05,0.05,
∴调查的200名学生学习时间的人数频率分布表如表:
学习时间
[0,40)
[40,80)
[80,120)
[120,160)
[160,200)
[200,240]
频数
20
35
65
60
10
10
频率
0.1
0.175
0.325
0.3
0.05
0.05
平均值为:
20×0.1+60×0.175+100×0.325+140×0.3+180×0.05+220×0.05=107.
(Ⅱ)由题意A类学生抽取人数为53(人),
将A类学生分别记为x,y,z,B类学生分别记为a,b,
设“选中的2人都是A类学生”为事件A,
则从5名学生中任选2人,所有可能情况有10种,分别为:
(x,y),(x,z),(x,a),(x,b),(y,z),(y,a),(y,b),(z,a),(z,b),(a,b),
其中事件A包含的基本事件有3种,分别为:(x,y),(x,z),(y,z),
∴从这五人中抽取的两人都是A类学生的概率为:
P(A).
18.【解答】解:(1)根据题意,任取两个不同的数字,(2,3),(2,8),(2,9),(3,8),(3,9),(8,9)所有的基本事件共有6个,
若a+b为奇数,则a和b一个是奇数一个是偶数,共有4种情况,
故所求的概率为.
(2)由题意知本题是一个几何概型问题,试验的全部结果构成区域Ω={a|﹣5≤a≤5},其长度为10,
若关于x的一元二次方程x2﹣ax+4=0没有实根,则Δ=a2﹣4×4<0,解得﹣4<a<4.
因此,所求的概率为.
19.【解答】解:(1)点P(6,4)关于轴的对称点的坐标P1(6,﹣4),
则反射光线所在的直线过点P1和Q,所以k1,
所以反射光线QH的方程为y=﹣(x﹣2),即y=﹣x+2.
(2)由题意,从甲罐、乙罐中分别随机抽取1个小球,共包含20个基本事件;
“抽取的两个小球标号之和大于5”包含的基本事件有:(1,5),(1,6),(2,5),(2,6),(3,3),(3,5),(3,6),(4,2),(4,3),(4,5),(4,6),共11个基本事件;
“抽取的两个小球标号之积大于8”包含的基本事件有:(2,5),(2,6),(3,3),(3,5),(3,6),(4,3),(4,5),(4,6),共8个基本事件;
即事件B是事件A的子事件;所以事件A∪B包含的基本事件个数为11个,
所以事件A∪B发生的概率为.
20.【解答】解:(1)设小华同学任取一个小球,抽得一等奖、二等奖、三等奖、不中奖的事件分别为A,B,C,D,
它们彼此是互斥事件,
由题意得P(A),P(B+C)=P(B)+P(C),
由对立事件的概率公式得P(D)=1﹣P(A+B+C)=1﹣P(B+C)﹣P(A)=1,
∴不能中奖的概率为.
(2)∵P(A+B),又P(A+B)=P(A)+P(B),
∴P(B),
∵P(B+C)=P(B)+P(C),
∴P(C),
∴中三等奖的概率为,
∴黄球个数为164(个).
21.【解答】解:(1)设测试成绩在[80,85)内的频率为x,根据所给的频率分布直方图可得,
0.01×5+0.07×5+0.06×5+x+0.02×5=1,解得x=0.2.
(2)第三、四、五组同学的数量之比为
0.3:0.2:0.1=3:2:1,
故抽取的这6名同学中,第三、四、五组同学的数量分别为3,2,1.
在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,所有的抽法共有15种,
而第四组至少有一名同学被抽中的抽法有?9种,
第四组至少有一名同学被抽中的概率为
.
22.【解答】解:(1)s=82.78,s=87.18,2s=80.58,2s=89.38,3s=78.38,3s=91.58,
由图表知,P(s<ds)0.80>0.68,P(2s<d2s)0.95≥0.95;P(3s<d3s)0.98<0.99,
所以该自动化设备的等级为B.
(2)直径尺寸在(2s,2s)之外的零件共5件,分别记为A,B,C,a,b,其中a,b为直径尺寸在(3s,3s)之外的零件,
从5件零件中随意抽取2件,所有情况:{A,B},{A,C},{A,a},{A,b},{B,C},{B,a},{B,b},{C,a},{C,b},{a,b},共10种,
至少有一个在(3s,3s)之外的所有情况:{A,a},{A,b},{B,a},{B,b},{C,a},{C,b},{a,b},共7种,
记至少有1件直径尺寸在(3s,3s)之外为事件Y,
则.
23.【解答】解:(1)∵以10%的比例对高二年级500名学生按选修物理和选修历史进行分层抽样,
∴该校高二年级选修物理的人数约为:
(6+9+9+3+2+1)×10=300(人),
∴该校高二年级选修历史的人数约为:500﹣300=200(人).
(2)样本中,阅读时间在60分钟以上的人数为:
(3+2+1)+(9+6+1)=22(人),
∵样本总数为:10%×500=50,
∴样本中阅读时间在60分钟以上的频率为:.
(3)样本中阅读时间在60~90分钟的选修物理的学生分两类:
一类是阅读时间在60~75分钟的共有3人,记为a1,a2,a3,
另一类是阅读时间在75~90分钟的共有2人,记为b1,b2,
从这5人中任选2人,共有10种等可能基本事件,分别为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2),
记事件A为:“至少有1人阅读时间在75~90之间”,
则事件为:“2人阅读都在60~75之间”,且包含3个基本事件:
(a1,a2),(a1,a3),(a2,a3),
∴至少有1人阅读时间在75~90之间的概率为:
P=1﹣P()=1.
24.【解答】解:(Ⅰ)选派乙参加数学竞赛较合适.
理由如下:
由题知83,
∴甲成绩的方差()2=50.8,
乙成绩的方差48.8,
由,,可知甲乙平均分相同,但乙的成绩比甲稳定,
故选派乙参加数学竞赛较合适.
(Ⅱ)5道备选题中学生会的3道分别记为a,b,c,不会的2道分别记为E,F,
方案一:学生从5道备选题中任意抽出1道的结果有:a,b,c,E,F,共5
种,
抽中会的备选题的结果有a,b,c,共3种,
∴此方案学生可参加复赛的概率P1.
方案二:学生从5道备选题中任意抽出3道的结果有:
(a,b,c),(a,b,E),(a,b,F),(a,c,E),(a,c,F),(a,E,F),(b,c,E),(b,c,F),(b,E,F),(c,E,F),共10种,
抽中至少2道会的备选题的结果有:
(a,b,c),(a,b,E),(a,b,F),(a,c,E),(a,c,F),(b,c,E),(b,c,F),共7种,
∴此方案学生可参加复赛的概率P2.
∵P1<P2,∴推荐的选手选择方案二答题方案进入复赛的可能性更大.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修三同步必刷题提高练
第三章《概率》
3.2
古典概型
一.选择题
1.(2020秋?南关区校级期末)2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款、法国8款、荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国.A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香烃矿物油成分,则随机抽取3袋,恰有2袋含有芳香烃矿物油成分的概率为( )
A.
B.
C.
D.
2.(2020秋?湖北月考)党的十八大要求全面实施素质教育,培养德智体美劳全面发展的社会主义建设者和接班人,劳动教育受到全社会广泛关注.某学校的某班级将5名同学分配到甲、乙、丙三个村参加劳动锻炼,每个村至少分配一位同学,则甲村恰好分配2位同学的概率为( )
A.
B.
C.
D.
3.(2020秋?垫江县校级月考)马林?梅森(MarinMersenne,1588﹣1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物.梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为纪念梅森在数论方面的这一贡献,将形如2p﹣1(其中p是素数)的素数,称为梅森素数.在不超过50的素数中,随机选取两个不同的数,至少有一个为梅森素数的概率是( )
A.
B.
C.
D.
4.(2020秋?建邺区校级月考)若从甲、乙、丙、丁4人中选出3名代表参加学校会议,则甲被选中的概率为( )
A.
B.
C.
D.
5.(2020?Ⅱ卷模拟)《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“─”表示一个阳爻,“﹣﹣”表示一个阴爻).若从含有两个及以上阳爻的卦中任取两卦,这两卦的六个爻中都恰有两个阳爻的概率为( )
A.
B.
C.
D.
6.(2020?青羊区校级模拟)从2名男生和3名女生中任选三人参加比赛,选中1名男生和2名女生的概率为( )
A.
B.
C.
D.
7.(2020?合肥二模)为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着A,B,C三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择A,B,C三个项目的意向如表:
扶贫项目
A
B
C
选择意向贫困户
甲、乙、丙、丁
甲、乙、丙
丙、丁
若每个贫困户只能从自己登记的选择意向中随机选取一项,且每个项目至多有两户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.
B.
C.
D.
8.(2020?梧州模拟)数学与文学有许多奇妙的联系,如诗中有回文诗:“儿忆父兮妻忆夫”,既可以顺读也可以逆读,数学中有回文数,如343、12521等,两位数的回文数有11、22、33、…、99共9个,则三位数的回文数中为偶数的概率是( )
A.
B.
C.
D.
二.填空题
9.(2020秋?历城区校级期中)已知7件产品中有5件合格品,2件次品.为找出这2件次品,每次任取一件检验,检验后不放回,则“恰好第一次检验出正品且第五次检验出最后一件次品”的概率为
.
10.(2020秋?浦东新区校级月考)有五张写有1、2、3、4、5的卡片,每次抽取1张记好数字后放回,这样抽4次,则抽到的最大数与最小数的差小于4的概率是
.
11.(2020?北京自主招生)从0﹣9共10个数中任取5个组成一个5位或4位(0在首位)数,则该数被396整除概率为
.
12.(2020秋?闵行区校级月考)我校5位同学报考了北京大学“强基计划”第I专业组,并顺利通过各项考核,已知5位同学将根据综合成绩和志愿顺序随机地进入教学类、物理学类、力学类这三个专业中的某一个专业,则这三个专业都有我校学生的概率是
(结果用最简分数表示).
13.(2020春?闵行区校级月考)假设一个随机数发生器一次只能从1,2,3,…,9这九个数学中等可能地选一个数,则该随机数发生器完成了n(n>1)次选择后,选出的n个数的乘积能被10整除的概率为
(用含n的代数式示).
14.(2020秋?浙江月考)甲从集合{1,2,3,4,5,6,7,8,9}中任取三个不同的元素,并按降序排列得到十进制三位数a,乙从集合{1,2,3,4,5,6,7,8}中任取三个不同的元素,按降序排列得到十进制三位数b,则a>b的概率为
.
15.(2020?普陀区三模)若实数a、b、c满足═,则a,b,c是调和的.设含有三个元素的集合P是集合M={x||x|≤2020,x∈Z}的子集,当集合P中的元素a、b、c既是等差的又是调和的时,称集合P为“好集”.则三元子集中“好集”的概率是
.
16.(2020春?滨海县校级期末)某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为
.
三.解答题
17.(2021?八模拟)2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗击疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课,每天共240分钟,请学生自主学习.区教育局为了了解学生网上学习情况,上课几天后在全区学生中采取随机抽样的方法抽取了200名学生进行问卷调查,为了方便表述把学习时间在[0,120)分钟的学生称为A类,把学习时间在[120,240]分钟的学生称为B类,调查的200名学生学习时间的人数频率分布表如表:
学习时间
[0,40)
[40,80)
[80,120)
[120,160)
[160,200)
[200,240]
频数
20
35
n
60
10
10
频率
以频率估计概率回答下列问题:
(Ⅰ)求表中n的值并完成上表,并估算这200名学生学习时间的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(Ⅱ)在A,B两类学生中,按分层抽样的方法从上述200名学生中抽取5人,求从这五人中抽取的两人都是A类学生的概率.
18.(2020秋?广西期中)(1)从2,3,8,9中任取两个不同的数字,分别记为a,b,求a+b为奇数的概率;
(2)已知a∈[﹣5,5],关于x的一元二次方程x2﹣ax+4=0,求此方程没有实根的概率.
19.(2020秋?湖北期中)(1)一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射后与y轴交于点H,求反射光线QH所在直线的方程.
(2)已知甲罐中有四个相同的小球,标号为1,2,3,4;乙罐中有五个相同的小球,标号为1,2,3,5,6,现从甲罐、乙罐中分别随机抽取1个小球,记事件A=“抽取的两个小球标号之和大于5”,事件B=“抽取的两个小球标号之积大于8”,求事件“A∪B”发生的概率.
20.(2020秋?聊城期中)某次联欢会上设有一个抽奖游戏抽奖箱中共有16个四种不同颜色且形状大小完全相同的小球,分别代表﹣等奖、二等奖、三等奖、无奖四种奖项.其中红球代表一等奖且只有1个,黄球代表三等奖.从中任取一个小球,若中二等奖或三等奖的概率.小华同学获得一次摸奖机会.
(1)求他不能中奖的概率;
(2)若该同学中一等奖或二等奖的概率是,试计算黄球的个数.
21.(2020秋?辽源期末)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的概率.
22.(2020秋?湖南月考)某质量检测部门为评估工厂某自动化设备生产零件T的性能情况,从该自动化设备生产零件T的流水线上随机抽取100件零件T为样本,测量其直径后,整理得到如表:
直径(单位:mm)
78
79
81
82
83
84
85
件数
1
1
3
5
6
19
33
直径(单位:mm)
86
87
88
89
90
91
93
件数
18
4
4
3
1
1
1
经计算,样本的平均值84.98,标准差s=2.2,用频率值作为概率的估计值.
(1)从该自动化设备加工的零件T中任意抽取一件,记其直径为d,根据下列不等式评估该自动化设备的性能:①P(s<ds)≥0.68;②P(2s<d2s)≥0.95;P(3s<d3s)≥0.99(P表示相应事件的概率).等级评估方法为:若同时满足上述三个式子,则自动化设备等级为A;若仅满足其中两个,自动化设备等级为B;若仅满足其中一个,则自动化设备等级为C;若全部都不满足,则自动化设备等级为D.试评估该自动化设备性能的等级情况;
(2)从样本中直径尺寸在(2x,2s)之外的零件T中随机抽取2件,求至少有1件直径尺寸在(3s,3s)之外的概率.
23.(2020春?通州区期末)为了解学生“课外阅读日”的活动情况,某校以10%的比例对高二年级500名学生按选修物理和选修历史进行分层抽样调查,测得阅读时间(单位:分钟)的频数统计图如图:
(1)分别估计该校高二年级选修物理和选修历史的人数;
(2)估计该校高二年级学生阅读时间在60分钟以上的概率;
(3)从样本中阅读时间在60~90分钟的选修物理的学生中任选2人,求至少有1人阅读时间在75~90之间的概率.
24.(2020春?咸阳期末)某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人5次数学考试的成绩,统计结果如表:
第一次
第二次
第三次
第四次
第五次
甲的成绩(分)
80
85
71
92
87
乙的成绩(分)
90
76
75
92
82
(Ⅰ)已知甲、乙两名学生这5次数学考试成绩的平均分都为83分,若从甲、乙两名学生中选一人参加数学竞赛,请从统计学的角度考虑,你认为选谁参加数学竞赛较合适?并说明理由;
(Ⅱ)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.
已知学生甲、乙都只会5道备选题中的3道,那么你推荐的选手选择哪种答题方案进入复赛的可能性更大?并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:记6袋奶粉中,不含芳香烃矿物油成分的奶粉为A、B,含芳香烃矿物油成分的奶粉为a、b、c、d,
任取3袋,所有的情况为:
(A,B,a),(A,B,b),(A,B,c),(A,B,d),(A,a,b),(A,a,c),(A,a,d),
(A,b,c),(A,b,d),(A,c,d),(B,a,b),(B,a,c),(B,a,d),(B,b,c),
(B,b,d),(B,c,d),(a,b,c),(a,b,d),(a,c,d),(b,c,d),共20种,
其中恰有2袋含有芳香烃矿物油成分包含的基本事件有:
(A,a,b),(A,a,c),(A,a,d),(A,b,c),(A,b,d),(A,c,d),(B,a,b),
(B,a,c),(B,a,d),(B,b,c),(B,b,d),(B,c,d),共12种,
故恰有2袋含有芳香烃矿物油成分的概率为:.
故选:D.
2.【解答】解:某学校的某班级将5名同学分配到甲、乙、丙三个村参加劳动锻炼,
每个村至少分配一位同学,
基本事件总数n150,
其中甲村恰好分配2位同学包含的基本事件个数m60,
∴甲村恰好分配2位同学的概率为P.
故选:B.
3.【解答】解:在不超过50的素数有:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,共15个,
其中梅森素数有:3,7,31,共3个,
在不超过50的素数中,随机选取两个不同的数包含的基本事件个数n105,
至少有一个为梅森素数包的基本事件个数m39.
∴至少有一个为梅森素数的概率P.
故选:B.
4.【解答】解:从甲,乙,丙,丁4位同学中选出3名代表参加学校会议,
基本事件总数n4,
甲被选中包含的基本事件个数m3,
则甲被选中的概率p.
故选:D.
5.【解答】解:含有两个阳爻的卦有3个,含有三个阳爻的卦有1个,
从含有两个及以上阳爻的卦中任取两卦,
基本事件总数n6,
这两卦的六个爻中都恰有两个阳爻包含的基本事件个数m3,
∴这两卦的六个爻中都恰有两个阳爻的概率为p.
故选:B.
6.【解答】解:记2名男生为A1,A2,3名女生为B1,B2,B3,
所有的结果为:A1A2B1,A1A2B2,A1A2B3,A1B1B2,A1B1B3,
A1B2B3,A2B1B2,A2B1B3,A2B2B3,B1B2B3,一共有10种情况,
符合条件的有:A1B1B2,A1B1B3,A1B2B3,
A2B1B2,A2B1B3,A2B2B3,共6种情况,
所以概率为,
故选:C.
7.【解答】解:由题意:甲乙只能选A,B项目,丁只能选A,C项目,丙则都可以.
由题意基本事件可分以下三类:
(1)甲乙都选A,则丁只能选C,丙则可以选B,C任一个,故共有2种方法;
(2)甲乙都选B,则丁可以选A或C,丙也可选A或C,故共有种方法.
(3)甲乙分别选AB之一,然后丁选A时,丙只能选B或C;丁选C时,丙则A,B,C都可以选.故有种方法.
故基本事件共有2+4+10=16种.
甲乙选同一种项目的共有2+4=6种.
故甲乙选同一项目的概率P.
故选:A.
8.【解答】解:三位数的回文数为ABA,
A共有1到9共9种可能,即1B1、2B2、3B3…
B共有0到9共10种可能,即A0A、A1A、A2A、A3A、…
共有9×10=90个,
其中偶数为A是偶数,共4种可能,即2B2,4B4,6B6,8B8,
B共有0到9共10种可能,即A0A、A1A、A2A、A3A、…
其有4×10=40个,
∴三位数的回文数中,偶数的概率P;
故选:D.
二.填空题
9.【解答】解:考查两件次品的位置,共有n21种取法,
因为恰好第五次取出最后一件次品,
依题意另一件次品只能排2,3,4位,共有m3种取法.
故“恰好第一次检验出正品且第五次检验出最后一件次品”的概率为p.
故答案为:.
10.【解答】解:有五张写有1、2、3、4、5的卡片,每次抽取1张记好数字后放回,这样抽4次,
共有54种不同的取法,差值可能为1,2,3,4,
最大数与最小数的差等于4,则4次抽取中5或1没有抽到,
没有抽到1的有44,没有抽到5的有44,5和1都没有抽到的有34,
所以抽到的最大数与最小数的差小于4有2×44﹣34种,
所以抽到的最大数与最小数的差小于4的概率.
故答案为:.
11.【解答】解:396=9×4×11,
先考虑被9整除的组合,
(1,8),(2,7),(3,6),(4,5),任意两组,加上0,9,(1)
(1,2,3,4,8),(1,2,3,5,7),(1,2,4,5,6),(2)
(1,2,6),(1,3,5),(2,3,4),加上0,9,(3)
再考虑被11整除,(1)中只能加0,
最后考虑被4整除,(1,2,3,5,7)舍去,(1,3,5)加上0,9舍去,
(1)中所有情况数为:48,
(2)中所有情况数为:8,
(3)中所有情况数为8,
综上共有:8+8+48=64种情况,
∴该数被396整除概率为P.
故答案为:.
12.【解答】解:5位同学将根据综合成绩和志愿顺序随机地进入教学类、物理学类、力学类这三个专业中的某一个专业,
基本事件总数n=35=243,
这三个专业都有我校学生包含的情况有两种,各个专业的学生数分别为1,1,3和2,2,1,
∴这三个专业都有我校学生包含的基本事件个数m=()?150,
则这三个专业都有我校学生的概率是p.
故答案为:.
13.【解答】解:要便n个数之积平衡车10整除,必须有一个数是5,有一个数是偶数,
n次选择的方法总共有9n种,其中:
A、每一次均不取5的取法,有8n种,
B、每一次均不取偶数的取法,有5n种,
C、每一次均在{1,3,7,9}中取数的方法有4n种,
由题意中C中的取法既包含于A,也包含于B,
∴该随机数发生器完成了n(n>1)次选择后,选出的n个数的乘积能被10整除的概率为:
P=1.
故答案为:1.
14.【解答】解:甲从集合{1,2,3,4,5,6,7,8,9}中任取三个不同的元素,并按降序排列得到十进制三位数a,
共有84种情况,
乙从集合{1,2,3,4,5,6,7,8}中任取三个不同的元素,按降序排列得到十进制三位数b,
共有56种情况,
故三位数a,b进行比较可得到84×56种情况,
乙取到的三位数甲都能取到,若乙取到的数是123,这在甲中是取得的最小的三位数,
则在甲取得的数中,除了123外,其它的数都比123大,共有84﹣1=83种情况,
当乙取得其它数时,分析同理,则可以得到在所有数的比较中,a>b的情况共有:
83+82+81+…+29+28种,
故a>b的概率为,
故答案为:.
15.【解答】解:因为P为三元素集合,
所以实数a,b,c互不相等,且均不为0,
根据题意可得,得2b2﹣ab﹣a2=0,
解得a=b(舍),或a=﹣2b,则c=4b
所以集合P={b,﹣2b,4b},
又因为含有三个元素的集合P是集合M={x||x|≤2020,x∈Z}的子集,
所以﹣2020≤4b≤2020,即﹣505≤b≤505,且b≠0
所以集合P的个数为:2×505=1010,
集合M中共由4041个元素,
所以三元子集中“好集”的概率是,
故答案为:.
16.【解答】解:我们把从顶点A到3的路线图单独画出来:
分析可得,
从顶点A到3总共有C52=10种走法,每一种走法的概率都是,
∴珠子从出口3出来是()5.
三.解答题
17.【解答】解:(Ⅰ)由题知被调查者一共200人,
∴35+60+n+20+10+10=200,解得n=65.
则被调查人员各组学习时间的频率分别为0.1,0.175,0.325,0.3,0.05,0.05,
∴调查的200名学生学习时间的人数频率分布表如表:
学习时间
[0,40)
[40,80)
[80,120)
[120,160)
[160,200)
[200,240]
频数
20
35
65
60
10
10
频率
0.1
0.175
0.325
0.3
0.05
0.05
平均值为:
20×0.1+60×0.175+100×0.325+140×0.3+180×0.05+220×0.05=107.
(Ⅱ)由题意A类学生抽取人数为53(人),
将A类学生分别记为x,y,z,B类学生分别记为a,b,
设“选中的2人都是A类学生”为事件A,
则从5名学生中任选2人,所有可能情况有10种,分别为:
(x,y),(x,z),(x,a),(x,b),(y,z),(y,a),(y,b),(z,a),(z,b),(a,b),
其中事件A包含的基本事件有3种,分别为:(x,y),(x,z),(y,z),
∴从这五人中抽取的两人都是A类学生的概率为:
P(A).
18.【解答】解:(1)根据题意,任取两个不同的数字,(2,3),(2,8),(2,9),(3,8),(3,9),(8,9)所有的基本事件共有6个,
若a+b为奇数,则a和b一个是奇数一个是偶数,共有4种情况,
故所求的概率为.
(2)由题意知本题是一个几何概型问题,试验的全部结果构成区域Ω={a|﹣5≤a≤5},其长度为10,
若关于x的一元二次方程x2﹣ax+4=0没有实根,则Δ=a2﹣4×4<0,解得﹣4<a<4.
因此,所求的概率为.
19.【解答】解:(1)点P(6,4)关于轴的对称点的坐标P1(6,﹣4),
则反射光线所在的直线过点P1和Q,所以k1,
所以反射光线QH的方程为y=﹣(x﹣2),即y=﹣x+2.
(2)由题意,从甲罐、乙罐中分别随机抽取1个小球,共包含20个基本事件;
“抽取的两个小球标号之和大于5”包含的基本事件有:(1,5),(1,6),(2,5),(2,6),(3,3),(3,5),(3,6),(4,2),(4,3),(4,5),(4,6),共11个基本事件;
“抽取的两个小球标号之积大于8”包含的基本事件有:(2,5),(2,6),(3,3),(3,5),(3,6),(4,3),(4,5),(4,6),共8个基本事件;
即事件B是事件A的子事件;所以事件A∪B包含的基本事件个数为11个,
所以事件A∪B发生的概率为.
20.【解答】解:(1)设小华同学任取一个小球,抽得一等奖、二等奖、三等奖、不中奖的事件分别为A,B,C,D,
它们彼此是互斥事件,
由题意得P(A),P(B+C)=P(B)+P(C),
由对立事件的概率公式得P(D)=1﹣P(A+B+C)=1﹣P(B+C)﹣P(A)=1,
∴不能中奖的概率为.
(2)∵P(A+B),又P(A+B)=P(A)+P(B),
∴P(B),
∵P(B+C)=P(B)+P(C),
∴P(C),
∴中三等奖的概率为,
∴黄球个数为164(个).
21.【解答】解:(1)设测试成绩在[80,85)内的频率为x,根据所给的频率分布直方图可得,
0.01×5+0.07×5+0.06×5+x+0.02×5=1,解得x=0.2.
(2)第三、四、五组同学的数量之比为
0.3:0.2:0.1=3:2:1,
故抽取的这6名同学中,第三、四、五组同学的数量分别为3,2,1.
在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,所有的抽法共有15种,
而第四组至少有一名同学被抽中的抽法有?9种,
第四组至少有一名同学被抽中的概率为
.
22.【解答】解:(1)s=82.78,s=87.18,2s=80.58,2s=89.38,3s=78.38,3s=91.58,
由图表知,P(s<ds)0.80>0.68,P(2s<d2s)0.95≥0.95;P(3s<d3s)0.98<0.99,
所以该自动化设备的等级为B.
(2)直径尺寸在(2s,2s)之外的零件共5件,分别记为A,B,C,a,b,其中a,b为直径尺寸在(3s,3s)之外的零件,
从5件零件中随意抽取2件,所有情况:{A,B},{A,C},{A,a},{A,b},{B,C},{B,a},{B,b},{C,a},{C,b},{a,b},共10种,
至少有一个在(3s,3s)之外的所有情况:{A,a},{A,b},{B,a},{B,b},{C,a},{C,b},{a,b},共7种,
记至少有1件直径尺寸在(3s,3s)之外为事件Y,
则.
23.【解答】解:(1)∵以10%的比例对高二年级500名学生按选修物理和选修历史进行分层抽样,
∴该校高二年级选修物理的人数约为:
(6+9+9+3+2+1)×10=300(人),
∴该校高二年级选修历史的人数约为:500﹣300=200(人).
(2)样本中,阅读时间在60分钟以上的人数为:
(3+2+1)+(9+6+1)=22(人),
∵样本总数为:10%×500=50,
∴样本中阅读时间在60分钟以上的频率为:.
(3)样本中阅读时间在60~90分钟的选修物理的学生分两类:
一类是阅读时间在60~75分钟的共有3人,记为a1,a2,a3,
另一类是阅读时间在75~90分钟的共有2人,记为b1,b2,
从这5人中任选2人,共有10种等可能基本事件,分别为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2),
记事件A为:“至少有1人阅读时间在75~90之间”,
则事件为:“2人阅读都在60~75之间”,且包含3个基本事件:
(a1,a2),(a1,a3),(a2,a3),
∴至少有1人阅读时间在75~90之间的概率为:
P=1﹣P()=1.
24.【解答】解:(Ⅰ)选派乙参加数学竞赛较合适.
理由如下:
由题知83,
∴甲成绩的方差()2=50.8,
乙成绩的方差48.8,
由,,可知甲乙平均分相同,但乙的成绩比甲稳定,
故选派乙参加数学竞赛较合适.
(Ⅱ)5道备选题中学生会的3道分别记为a,b,c,不会的2道分别记为E,F,
方案一:学生从5道备选题中任意抽出1道的结果有:a,b,c,E,F,共5
种,
抽中会的备选题的结果有a,b,c,共3种,
∴此方案学生可参加复赛的概率P1.
方案二:学生从5道备选题中任意抽出3道的结果有:
(a,b,c),(a,b,E),(a,b,F),(a,c,E),(a,c,F),(a,E,F),(b,c,E),(b,c,F),(b,E,F),(c,E,F),共10种,
抽中至少2道会的备选题的结果有:
(a,b,c),(a,b,E),(a,b,F),(a,c,E),(a,c,F),(b,c,E),(b,c,F),共7种,
∴此方案学生可参加复赛的概率P2.
∵P1<P2,∴推荐的选手选择方案二答题方案进入复赛的可能性更大.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
