第26章反比例函数专题二 反比例函数中的数学思想方法-人教版九年级数学下册同步练习(Word版 含解析)
文档属性
| 名称 | 第26章反比例函数专题二 反比例函数中的数学思想方法-人教版九年级数学下册同步练习(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 12:59:23 | ||
图片预览




文档简介
专题二
反比例函数中的数学思想方法
1.已知反比例函数y的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是( )
A.y1<y2<0
B.0<y2<y1
C.y1<0<y2
D.y2<0<y1
2.若M(﹣4,y1)、N(﹣2,y2)、P(2,y3)三点都在函数y(k<0)的图象上,则y1,y2,y3的大小关系为( )
A.y2>y3>y1
B.y2>y1>y3
C.y3>y1>y2
D.y3>y2>y1
3.已知:如图,两点A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b(k≠0)和反比例函数y(m≠0)图象的两个交点.
(1)求一次函数和反比例函数的的解析式.
(2)求△AOB的面积.
(3)观察图象,直接写出不等式kx+b的解集.
4.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y的解析式为
.
5.已知正比例函数y=kx的图象与反比例函数y(k为常数,k≠0)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标.
(2)若点A(x1,y1),B(x2,y2)是反比例函数y图象上的两点,且x1<x2,试比较y1,y2的大小.
6.已知,反比例函数y(k≠0)与正比例函数yx,在平面直角坐标系内相交于A、B两点,点A的坐标是(2,m).
(1)求m和k的值.
(2)求点B的坐标.
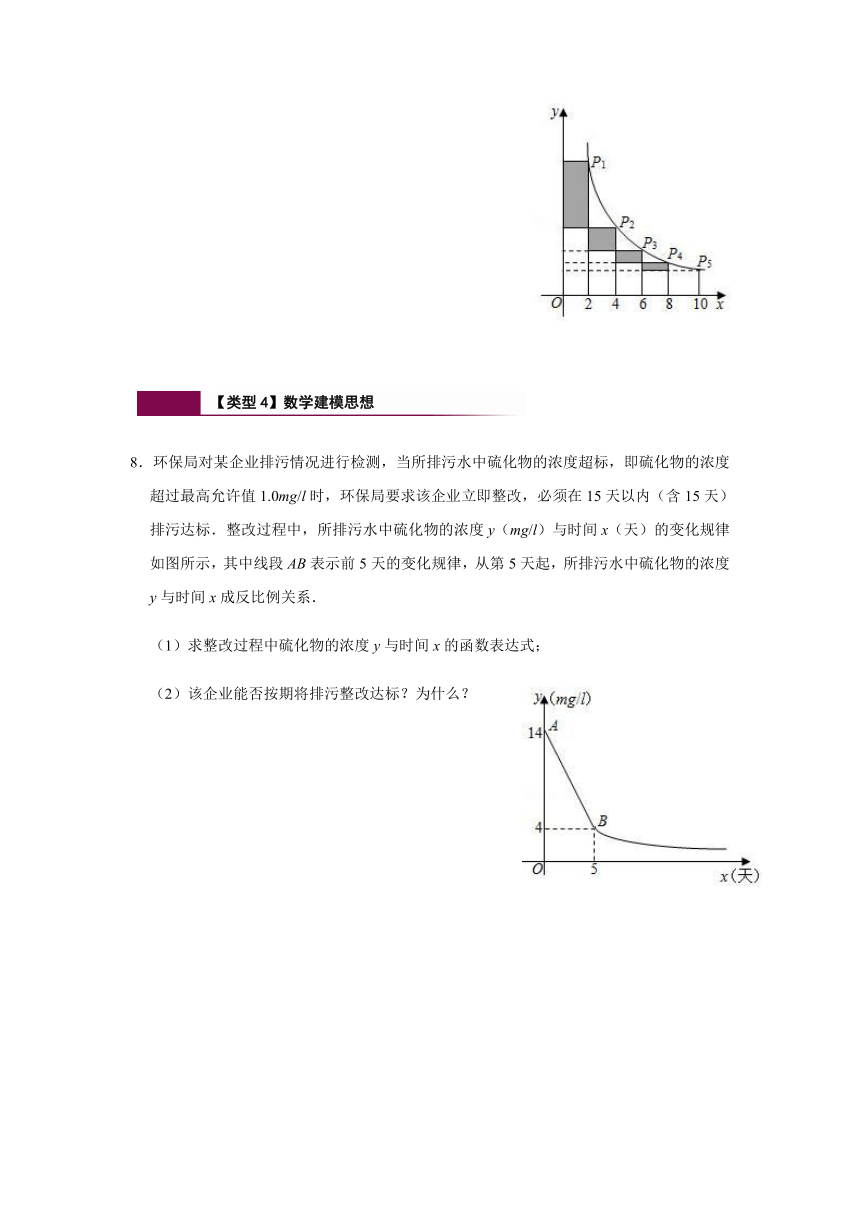
7.如图,在反比例函数y(x>0)的图象上有点P1,P2,P3,P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则点P1的坐标为
,阴影部分的面积S1+S2+S3+S4=
.
8.环保局对某企业排污情况进行检测,当所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许值1.0mg/l时,环保局要求该企业立即整改,必须在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/l)与时间x(天)的变化规律如图所示,其中线段AB表示前5天的变化规律,从第5天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业能否按期将排污整改达标?为什么?
9.心理学家研究发现,一般情况下,一节课45分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,BC∥x轴,CD为双曲线的一部分),其中AB段的关系式为y=2x+20.
(1)根据图中数据,求出CD段双曲线的关系式;
(2)一道数学竞赛题,需要讲20分钟,为了效果较好,要求学生的注意力指标数最低达到32,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
参考答案与试题解析
1.【解答】解:如图,
若x1<0<x2,则y2<0<y1.
故选:D.
2.【解答】解:∵k<0,故反比例函数图象的两个分支在第二四象限,且在每个象限内y随x的增大而增大.
又∵M(﹣4,y1)、N(﹣2,y2)是双曲线y(k<0)上的两点,且﹣4<﹣2<0,
∴0<y1<y2.
又∵2>0,P(2,y3)在第四象限,
∴y3<0,故y1,y2,y3的大小关系为y2>y1>y3.
故选:B.
3.【解答】解:(1)∵A(﹣4,2)在上,
∴m=﹣4×2=﹣8.
∴反比例函数的解析式为.
∵B(n,﹣4)在上,
∴n=2,
∵y=kx+b经过A(﹣4,2),B(2,﹣4),
∴,
解之得,
∴一次函数的解析式为y=﹣x﹣2;
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=﹣2.
∴点C(﹣2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO6;
(3)由图可得,不等式kx+b的解集为x≤﹣4或0<x≤2.
4.【解答】解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
设点A(﹣a,0)
∴AO=a,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣a,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣a,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣a,AO=GN=a,
∴AN=2,
∴点P(2﹣2a,﹣2),
∴直线OP解析式为:yx,
联立方程组
∴
∴点H的纵坐标为,
∴点E(﹣a,)
∵反比例函数y的图象过点E,
∴k=﹣a×(2,
∴反比例函数解析式为:y,
故答案为:y.
5.【解答】解:(1)将x=2代入正比例函数y=kx的图象与反比例函数y中,得:2k,
解得:k=﹣1,
∴正比例函数的表达式为y=x,反比例函数的表达式为y.
∴﹣x,
即x2=4,
得x=±2.
∴两函数图象交点的坐标为(2,﹣2),(﹣2,2);
(2)∵反比例函数y的图象分别在第二,四象限内,在每一象限内y的值随x值的增大而增大,
∴当x1<x2<0时,y1<y2,
当x1<0<x2时,因为y1,y2,所以y1>y2,
当0<x1<x2,时,y1<y2.
6.【解答】解:(1)∵点A(2,m)在正比例函数的图象上,
∴,
解得:m=﹣1.
∴点A的坐标为(2,﹣1);
∵点A(2,﹣1)在反比例函数的图象上,
∴k=﹣2;
(2)解得或,
∴点B的坐标为(﹣2,1).
7.【解答】解:当x=2时,y10,
∴点P1的坐标为(2,10),
如图所示,将右边三个矩形平移,
把x=10代入反比例解析式得:y=2,
∴P1C=AB=10﹣2=8,
则S1+S2+S3+S4=S矩形ABCP1=2×8=16,
故答案为:(2,10);16.
8.【解答】解:(1)由图象知,点A、B的坐标分别为(0,14)、(4,5),
当0≤x≤5时,设AB的表达式为y=kx+b,
将点A、B的坐标代入上式得,解得,
故y=﹣2x+14;
当x>5时,设函数的表达式为y,
把点B的坐标(4,5)代入上式并解得:k=20,
故y;
故函数的表达式为y;
(2)不能,理由:
当x=15时,y1,
故不能按期完成排污整改达标.
9.【解答】解:(1)∵AB段的关系式为y=2x+20,
∴当x=10时,y=40,
∴点B的坐标为(10,40),点C的坐标为(24,40),
设C、D所在双曲线的解析式为y2,
把C(24,40)代入得,k=960,
∴y.
(2)令y=2x+20=32,
∴32=2x+20,
∴x=6
令y32,
∴x=30,
∵30﹣6=24>20,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
反比例函数中的数学思想方法
1.已知反比例函数y的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是( )
A.y1<y2<0
B.0<y2<y1
C.y1<0<y2
D.y2<0<y1
2.若M(﹣4,y1)、N(﹣2,y2)、P(2,y3)三点都在函数y(k<0)的图象上,则y1,y2,y3的大小关系为( )
A.y2>y3>y1
B.y2>y1>y3
C.y3>y1>y2
D.y3>y2>y1
3.已知:如图,两点A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b(k≠0)和反比例函数y(m≠0)图象的两个交点.
(1)求一次函数和反比例函数的的解析式.
(2)求△AOB的面积.
(3)观察图象,直接写出不等式kx+b的解集.
4.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y的解析式为
.
5.已知正比例函数y=kx的图象与反比例函数y(k为常数,k≠0)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标.
(2)若点A(x1,y1),B(x2,y2)是反比例函数y图象上的两点,且x1<x2,试比较y1,y2的大小.
6.已知,反比例函数y(k≠0)与正比例函数yx,在平面直角坐标系内相交于A、B两点,点A的坐标是(2,m).
(1)求m和k的值.
(2)求点B的坐标.
7.如图,在反比例函数y(x>0)的图象上有点P1,P2,P3,P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则点P1的坐标为
,阴影部分的面积S1+S2+S3+S4=
.
8.环保局对某企业排污情况进行检测,当所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许值1.0mg/l时,环保局要求该企业立即整改,必须在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/l)与时间x(天)的变化规律如图所示,其中线段AB表示前5天的变化规律,从第5天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业能否按期将排污整改达标?为什么?
9.心理学家研究发现,一般情况下,一节课45分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,BC∥x轴,CD为双曲线的一部分),其中AB段的关系式为y=2x+20.
(1)根据图中数据,求出CD段双曲线的关系式;
(2)一道数学竞赛题,需要讲20分钟,为了效果较好,要求学生的注意力指标数最低达到32,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
参考答案与试题解析
1.【解答】解:如图,
若x1<0<x2,则y2<0<y1.
故选:D.
2.【解答】解:∵k<0,故反比例函数图象的两个分支在第二四象限,且在每个象限内y随x的增大而增大.
又∵M(﹣4,y1)、N(﹣2,y2)是双曲线y(k<0)上的两点,且﹣4<﹣2<0,
∴0<y1<y2.
又∵2>0,P(2,y3)在第四象限,
∴y3<0,故y1,y2,y3的大小关系为y2>y1>y3.
故选:B.
3.【解答】解:(1)∵A(﹣4,2)在上,
∴m=﹣4×2=﹣8.
∴反比例函数的解析式为.
∵B(n,﹣4)在上,
∴n=2,
∵y=kx+b经过A(﹣4,2),B(2,﹣4),
∴,
解之得,
∴一次函数的解析式为y=﹣x﹣2;
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=﹣2.
∴点C(﹣2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO6;
(3)由图可得,不等式kx+b的解集为x≤﹣4或0<x≤2.
4.【解答】解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
设点A(﹣a,0)
∴AO=a,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣a,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣a,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣a,AO=GN=a,
∴AN=2,
∴点P(2﹣2a,﹣2),
∴直线OP解析式为:yx,
联立方程组
∴
∴点H的纵坐标为,
∴点E(﹣a,)
∵反比例函数y的图象过点E,
∴k=﹣a×(2,
∴反比例函数解析式为:y,
故答案为:y.
5.【解答】解:(1)将x=2代入正比例函数y=kx的图象与反比例函数y中,得:2k,
解得:k=﹣1,
∴正比例函数的表达式为y=x,反比例函数的表达式为y.
∴﹣x,
即x2=4,
得x=±2.
∴两函数图象交点的坐标为(2,﹣2),(﹣2,2);
(2)∵反比例函数y的图象分别在第二,四象限内,在每一象限内y的值随x值的增大而增大,
∴当x1<x2<0时,y1<y2,
当x1<0<x2时,因为y1,y2,所以y1>y2,
当0<x1<x2,时,y1<y2.
6.【解答】解:(1)∵点A(2,m)在正比例函数的图象上,
∴,
解得:m=﹣1.
∴点A的坐标为(2,﹣1);
∵点A(2,﹣1)在反比例函数的图象上,
∴k=﹣2;
(2)解得或,
∴点B的坐标为(﹣2,1).
7.【解答】解:当x=2时,y10,
∴点P1的坐标为(2,10),
如图所示,将右边三个矩形平移,
把x=10代入反比例解析式得:y=2,
∴P1C=AB=10﹣2=8,
则S1+S2+S3+S4=S矩形ABCP1=2×8=16,
故答案为:(2,10);16.
8.【解答】解:(1)由图象知,点A、B的坐标分别为(0,14)、(4,5),
当0≤x≤5时,设AB的表达式为y=kx+b,
将点A、B的坐标代入上式得,解得,
故y=﹣2x+14;
当x>5时,设函数的表达式为y,
把点B的坐标(4,5)代入上式并解得:k=20,
故y;
故函数的表达式为y;
(2)不能,理由:
当x=15时,y1,
故不能按期完成排污整改达标.
9.【解答】解:(1)∵AB段的关系式为y=2x+20,
∴当x=10时,y=40,
∴点B的坐标为(10,40),点C的坐标为(24,40),
设C、D所在双曲线的解析式为y2,
把C(24,40)代入得,k=960,
∴y.
(2)令y=2x+20=32,
∴32=2x+20,
∴x=6
令y32,
∴x=30,
∵30﹣6=24>20,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
