第27章专题五 利用相似的性质解三角形中的内接多边形问题人教版九年级数学下册同步练习(Word版 含解析)
文档属性
| 名称 | 第27章专题五 利用相似的性质解三角形中的内接多边形问题人教版九年级数学下册同步练习(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 00:00:00 | ||
图片预览



文档简介
专题五
利用相似的性质解三角形中的内接多边形问题
1.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题.
画法:
①在△AOB内画等边△CDE使点C在OA上,点D在OB上;
②连结OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;
③连结C′D′,则△C′D′E′是△AOB的内接三角形.求证:△C′D′E′是等边三角形.
2.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15
B.20
C.25
D.30
3.如图,正三角形ABC的边长为3,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边CB上,点P、N分别在边CA、AB上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A.
B.
C.3
D.
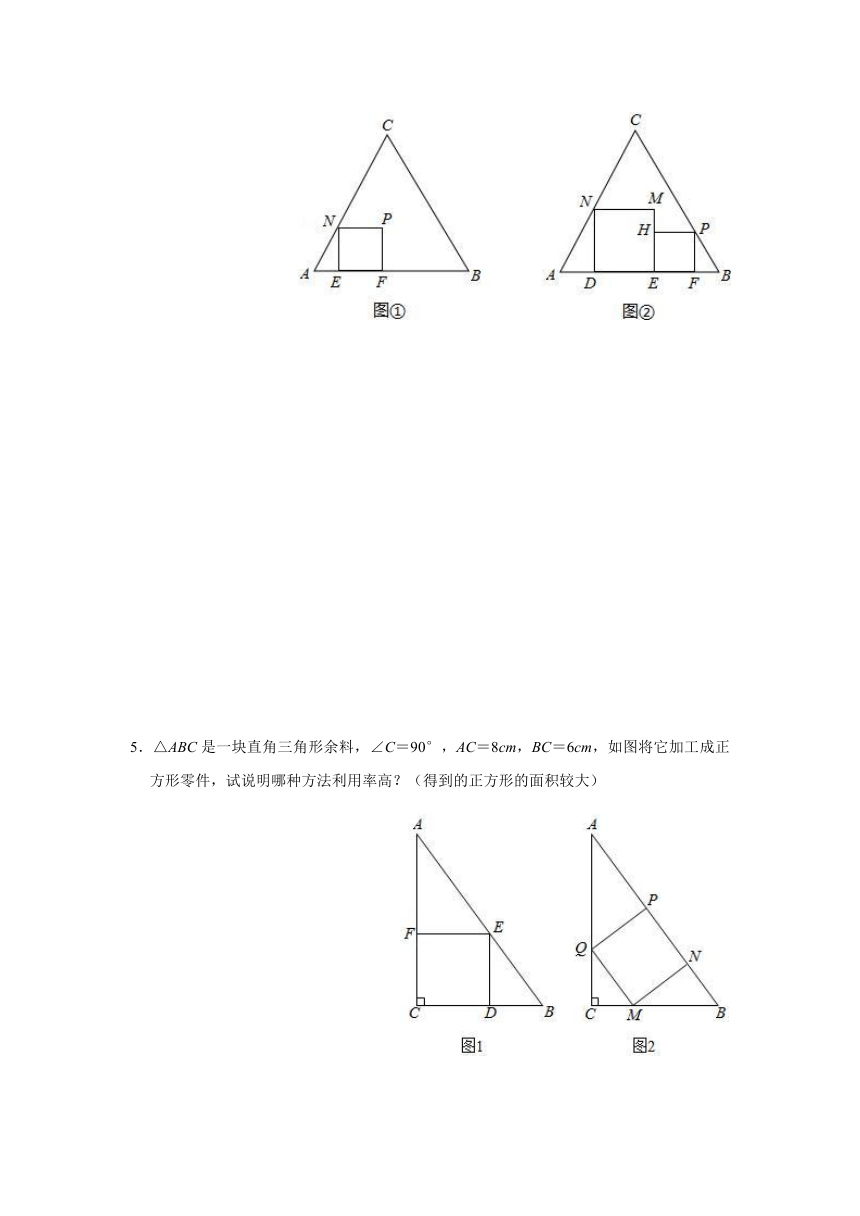
4.如图,正三角形ABC的边长为3.
(1)如图①,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE、EF在边AB上,点P、N分别在边CB、CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
5.△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
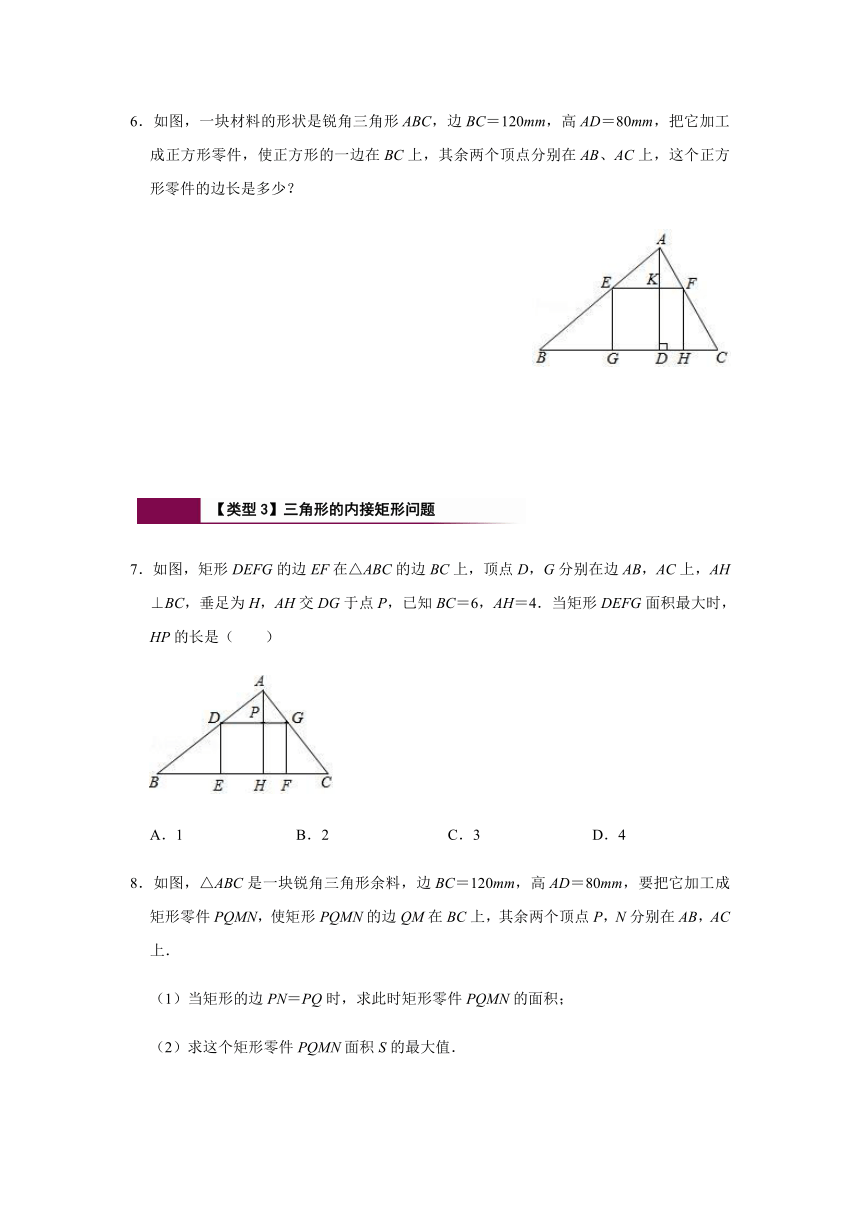
6.如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
7.如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
A.1
B.2
C.3
D.4
8.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
9.如图,要从一块Rt△ABC的白铁皮零料上截出一块矩形EFGH白铁皮.已知∠A=90°,AB=16cm,AC=12cm,要求截出的矩形的长与宽的比为2:1,且较长边在BC上,点E,F分别在AB,AC上,所截矩形的长和宽各是多少?
如图,有一块三角形余料ABC,它的边BC=18cm,高AD=12cm,现在要把它加工成长与宽的比为3:2的矩形零件EFCH,要求一条长边在BC上,其余两个顶点分别在AB,AC上,求矩形EFGH的周长.
参考答案与试题解析
1.证明:∵E′C′∥EC,E′D′∥ED,
∴△OCE∽△OC′E′,△ODE∽△OD′E′,
∴CE:C′E′=OE:OE′,DE:D′E′=OE:OE′,∠CEO=∠C′E′O,∠DEO=∠D′E′O,
∴CE:C′E′=DE:D′E′,∠CED=∠C′E′D′,
∴△CDE∽△C′D′E′,
∵△CDE是等边三角形,
∴△C′D′E′是等边三角形.
2.解:设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC,
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x,
∵△AEF∽△ABC,
∴(相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,
∴AN=60﹣x,
∴,
解得:x=40,
∴AN=60﹣x=60﹣40=20.
故选:B.
3.解:设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,
∵△ABC为等边三角形,
∴∠A=∠B=60°,AB=3,
在Rt△BDN中,BDDNm,
在Rt△CPF中,CFPFn,
∵BD+DE+EF+CF=AB,
∴m+m+nn=3,
∴m+n=3,
∴n=3﹣m,
∴S=m2+n2=m2+(3﹣m)2=2(m)2,
当点M落在AC上,则正方形DEMN的边长最小,正方形EFPH的边长最大,如图,
在Rt△BDN中,BDDN,BNDN,
∴DNDN=3,解得DN=33,
在Rt△CPF中,CFPF,
∴(33)+33+EFPF=3,
解得PF=69,
∴6﹣3m≤33,
∴当m时,S最小,S的最小值为.
故选:D.
4.解:(1)如图①,正方形E′F′P′N′即为所求.
(2)设正方形E′F′P′N′的边长为x,
∵△ABC为正三角形,
∴AE′=BF′x.
∵E′F′+AE′+BF′=AB,
∴xxx=3,
∴x,即x=33,(x≈2.20也正确)
(3)如图②,连接NE、EP、PN,则∠NEP=90°.
设正方形DEMN、正方形EFPH的边长分别为m、n(m≥n),
它们的面积和为S,则NE,PEn.
∴PN2=NE2+PE2=2m2+2n2=2(m2+n2).
∴S=m2+n2PN2,
延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m﹣n)2.
∵AD+DE+EF+BF=AB,即m+m+nn3,化简得m+n=3.
∴S[32+(m﹣n)2](m﹣n)2
①当(m﹣n)2=0时,即m=n时,S最小.
∴S最小;
②当(m﹣n)2最大时,S最大.
即当m最大且n最小时,S最大.
∵m+n=3,
由(2)知,m最大=33.
∴S最大[9+(m最大﹣n最小)2]
[9+(33﹣6+3)2]
=99﹣54.
(S最大≈5.47也正确)
综上所述,S最大=99﹣54,S最小.
5.解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴,即,
解得:x(cm),
即正方形BDEF边长为cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB10,
∵CH?ABAC?BC
∴CH(cm),
设正方形MNPQ边长为x,则QM=x,CJx,
∵QM∥AB,
∴△CMQ∽△CBA,
∴,即,
解得:x(cm),
即正方形BDEF边长为(cm);
∵,
∴图1利用率高.
6.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x
mm,则KD=EF=xmm,AK=(80﹣x)mm,
∵AD⊥BC,
∴,
∴,
解得:x=48.
答:正方形零件的边长为48mm.
7.解:设HP=x,则DE=GF=x,
∵四边形DEFG是矩形,
∴DG=EF,DE=GF=HP=x,DG∥EF,
∵AH⊥BC,
∴AH⊥DG,
∵DG∥EF,
∴△ADG∽△ABC,
∴,
∴,
解得:DG=6x,
∴矩形DEFG的面积S=DG×DE=(6x)x(x﹣2)2+6,
∵0,
∴S有最大值,当x=2时,S的最大值是6,
即当HP=2时,矩形DEFG的面积最大,
故选:B.
8.解:(1)设矩形零件PQMN的边PN=a,PQ=x,则AE=80﹣a.
∵PN∥BC,∴△APN∽△ABC.
∴.
因此,,
解得a=120x.
∴120x=x,
解得:x=48
所以长方形PQMN的面积S=xa=x(120x)x2+120x482+120×48=2304mm2
所以矩形零件PQMN的面积为2304mm2.
(2)由Sx2+120x,
当x40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
9.解:过点A作AN⊥BC交HF于点M,交BC于点N.
∵∠BAC=90°,
∴∠BNA=∠BAC,BC20(cm),
又∵∠B=∠B,
∴△ABN∽△CBA,
∴
∴AN(cm),
∵四边形EFGH是矩形,
∴EF∥HD,
∴∠AHF=∠B,∠AFM=∠C.
∴△AHF∽△ABC.
∴.
设EF=x,则MN=x,由截出的矩形的长与宽的比为2:1可知HF=2x.
.
解得x.
∴2x.
答:截得的矩形的长为cm,宽为cm.
10.解:∵矩形EFGH中,EH∥FG,EH=GF,
∴△AEH∽△ABC,
又∵AD⊥BC,
∴AM⊥EH,
∴,
设EH=3x,则MD=EF=2x,AM=12﹣2x,
∴,
解得:x=3,
∴EH=3x=9,EF=2x=6,
∴矩形EFGH的周长为:2×(9+6)=30(cm).
利用相似的性质解三角形中的内接多边形问题
1.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题.
画法:
①在△AOB内画等边△CDE使点C在OA上,点D在OB上;
②连结OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;
③连结C′D′,则△C′D′E′是△AOB的内接三角形.求证:△C′D′E′是等边三角形.
2.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15
B.20
C.25
D.30
3.如图,正三角形ABC的边长为3,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边CB上,点P、N分别在边CA、AB上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A.
B.
C.3
D.
4.如图,正三角形ABC的边长为3.
(1)如图①,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE、EF在边AB上,点P、N分别在边CB、CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
5.△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
6.如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
7.如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
A.1
B.2
C.3
D.4
8.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
9.如图,要从一块Rt△ABC的白铁皮零料上截出一块矩形EFGH白铁皮.已知∠A=90°,AB=16cm,AC=12cm,要求截出的矩形的长与宽的比为2:1,且较长边在BC上,点E,F分别在AB,AC上,所截矩形的长和宽各是多少?
如图,有一块三角形余料ABC,它的边BC=18cm,高AD=12cm,现在要把它加工成长与宽的比为3:2的矩形零件EFCH,要求一条长边在BC上,其余两个顶点分别在AB,AC上,求矩形EFGH的周长.
参考答案与试题解析
1.证明:∵E′C′∥EC,E′D′∥ED,
∴△OCE∽△OC′E′,△ODE∽△OD′E′,
∴CE:C′E′=OE:OE′,DE:D′E′=OE:OE′,∠CEO=∠C′E′O,∠DEO=∠D′E′O,
∴CE:C′E′=DE:D′E′,∠CED=∠C′E′D′,
∴△CDE∽△C′D′E′,
∵△CDE是等边三角形,
∴△C′D′E′是等边三角形.
2.解:设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC,
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x,
∵△AEF∽△ABC,
∴(相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,
∴AN=60﹣x,
∴,
解得:x=40,
∴AN=60﹣x=60﹣40=20.
故选:B.
3.解:设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,
∵△ABC为等边三角形,
∴∠A=∠B=60°,AB=3,
在Rt△BDN中,BDDNm,
在Rt△CPF中,CFPFn,
∵BD+DE+EF+CF=AB,
∴m+m+nn=3,
∴m+n=3,
∴n=3﹣m,
∴S=m2+n2=m2+(3﹣m)2=2(m)2,
当点M落在AC上,则正方形DEMN的边长最小,正方形EFPH的边长最大,如图,
在Rt△BDN中,BDDN,BNDN,
∴DNDN=3,解得DN=33,
在Rt△CPF中,CFPF,
∴(33)+33+EFPF=3,
解得PF=69,
∴6﹣3m≤33,
∴当m时,S最小,S的最小值为.
故选:D.
4.解:(1)如图①,正方形E′F′P′N′即为所求.
(2)设正方形E′F′P′N′的边长为x,
∵△ABC为正三角形,
∴AE′=BF′x.
∵E′F′+AE′+BF′=AB,
∴xxx=3,
∴x,即x=33,(x≈2.20也正确)
(3)如图②,连接NE、EP、PN,则∠NEP=90°.
设正方形DEMN、正方形EFPH的边长分别为m、n(m≥n),
它们的面积和为S,则NE,PEn.
∴PN2=NE2+PE2=2m2+2n2=2(m2+n2).
∴S=m2+n2PN2,
延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m﹣n)2.
∵AD+DE+EF+BF=AB,即m+m+nn3,化简得m+n=3.
∴S[32+(m﹣n)2](m﹣n)2
①当(m﹣n)2=0时,即m=n时,S最小.
∴S最小;
②当(m﹣n)2最大时,S最大.
即当m最大且n最小时,S最大.
∵m+n=3,
由(2)知,m最大=33.
∴S最大[9+(m最大﹣n最小)2]
[9+(33﹣6+3)2]
=99﹣54.
(S最大≈5.47也正确)
综上所述,S最大=99﹣54,S最小.
5.解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴,即,
解得:x(cm),
即正方形BDEF边长为cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB10,
∵CH?ABAC?BC
∴CH(cm),
设正方形MNPQ边长为x,则QM=x,CJx,
∵QM∥AB,
∴△CMQ∽△CBA,
∴,即,
解得:x(cm),
即正方形BDEF边长为(cm);
∵,
∴图1利用率高.
6.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x
mm,则KD=EF=xmm,AK=(80﹣x)mm,
∵AD⊥BC,
∴,
∴,
解得:x=48.
答:正方形零件的边长为48mm.
7.解:设HP=x,则DE=GF=x,
∵四边形DEFG是矩形,
∴DG=EF,DE=GF=HP=x,DG∥EF,
∵AH⊥BC,
∴AH⊥DG,
∵DG∥EF,
∴△ADG∽△ABC,
∴,
∴,
解得:DG=6x,
∴矩形DEFG的面积S=DG×DE=(6x)x(x﹣2)2+6,
∵0,
∴S有最大值,当x=2时,S的最大值是6,
即当HP=2时,矩形DEFG的面积最大,
故选:B.
8.解:(1)设矩形零件PQMN的边PN=a,PQ=x,则AE=80﹣a.
∵PN∥BC,∴△APN∽△ABC.
∴.
因此,,
解得a=120x.
∴120x=x,
解得:x=48
所以长方形PQMN的面积S=xa=x(120x)x2+120x482+120×48=2304mm2
所以矩形零件PQMN的面积为2304mm2.
(2)由Sx2+120x,
当x40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
9.解:过点A作AN⊥BC交HF于点M,交BC于点N.
∵∠BAC=90°,
∴∠BNA=∠BAC,BC20(cm),
又∵∠B=∠B,
∴△ABN∽△CBA,
∴
∴AN(cm),
∵四边形EFGH是矩形,
∴EF∥HD,
∴∠AHF=∠B,∠AFM=∠C.
∴△AHF∽△ABC.
∴.
设EF=x,则MN=x,由截出的矩形的长与宽的比为2:1可知HF=2x.
.
解得x.
∴2x.
答:截得的矩形的长为cm,宽为cm.
10.解:∵矩形EFGH中,EH∥FG,EH=GF,
∴△AEH∽△ABC,
又∵AD⊥BC,
∴AM⊥EH,
∴,
设EH=3x,则MD=EF=2x,AM=12﹣2x,
∴,
解得:x=3,
∴EH=3x=9,EF=2x=6,
∴矩形EFGH的周长为:2×(9+6)=30(cm).
