2020-2021学年北师大版九年级数学下册3.1---3.3 考点检测题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册3.1---3.3 考点检测题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 00:00:00 | ||
图片预览


文档简介
3.1圆
一、单选题
1.⊙O的半径为5,点P到圆心O的距离为4,点P与⊙O的位置关系是
A.无法确定
B.点P在⊙O外
C.点P在⊙O上
D.点P在⊙O内
2.已知,的半径为2,圆心为坐标原点,则点与的位置关系是(???)
A.点在上
B.点在内
C.点在外
D.不确定
3.已知⊙O的半径为10cm,点p到圆心O的距离为8cm,则点p和圆的位置关系(???)
A.点在圆内
B.点在圆外
C.点在圆上
D.无法判断
4.若的半径是,点在内,则的长可能是(???)
A.
B.
C.
D.
5.已知△ABC,以AB为直径作⊙O,∠C=88°,则点C在( )
A.⊙O上
B.⊙O外
C.⊙O
内
D.无法确定
6.点P到圆上各点的最大距离为10cm,最小距离为6cm,则此圆的半径为(???)
A.8cm
B.5cm或3cm
C.8cm或2cm
D.3cm
7.已知⊙O的半径r=3,点P和圆心O之间的距离为d,且方程没有实数根,则点P与⊙O的位置关系是(????)
A.在圆上
B.在圆内
C.在圆外
D.不能确定
8.到圆心的距离不大于半径的点的集合是(?)
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
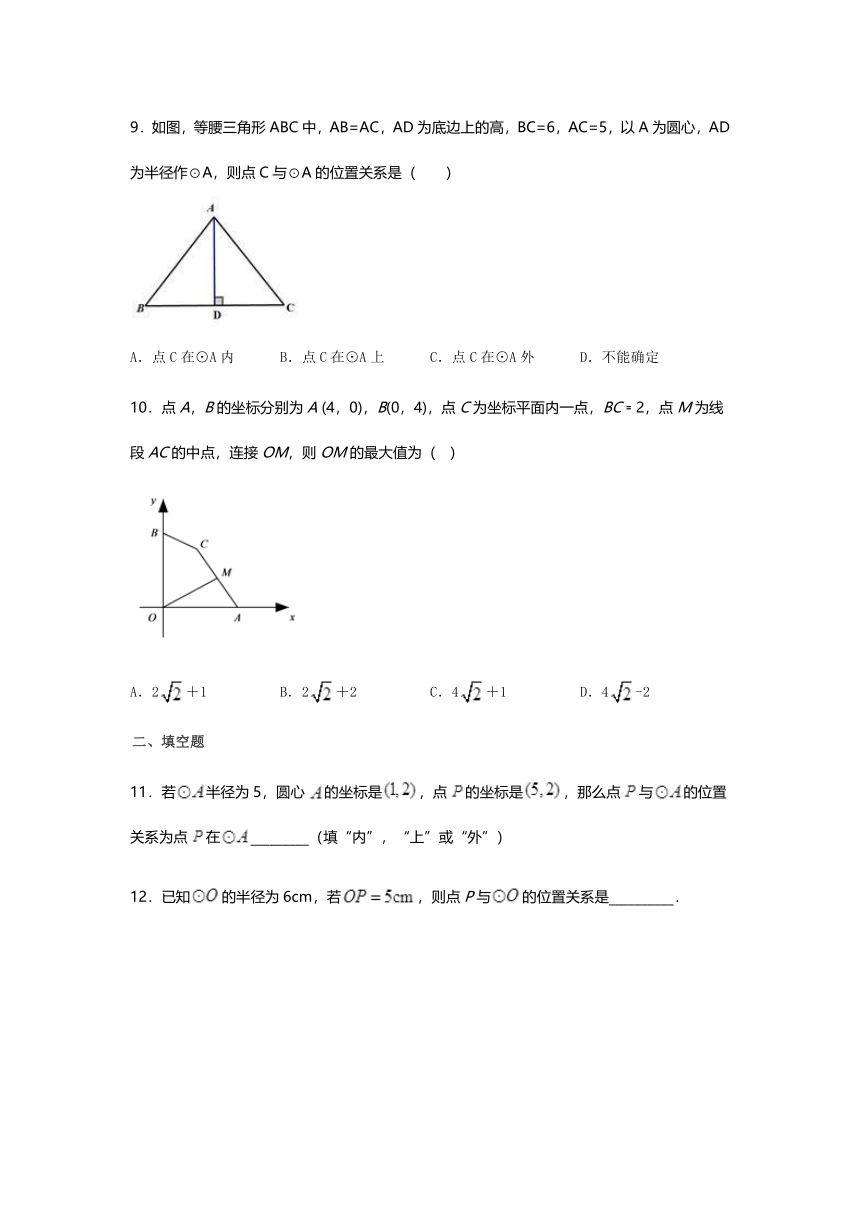
9.如图,等腰三角形ABC中,AB=AC,AD为底边上的高,BC=6,AC=5,以A为圆心,AD为半径作⊙A,则点C与⊙A的位置关系是( )
A.点C在⊙A内
B.点C在⊙A上
C.点C在⊙A外
D.不能确定
10.点A,B的坐标分别为A?(4,0),B(0,4),点C为坐标平面内一点,BC﹦2,点M为线段AC的中点,连接OM,则OM的最大值为(???)
A.2+1
B.2+2
C.4+1
D.4-2
二、填空题
11.若半径为5,圆心的坐标是,点的坐标是,那么点与的位置关系为点在_________(填“内”,“上”或“外”)
12.已知的半径为6cm,若,则点P与的位置关系是__________.
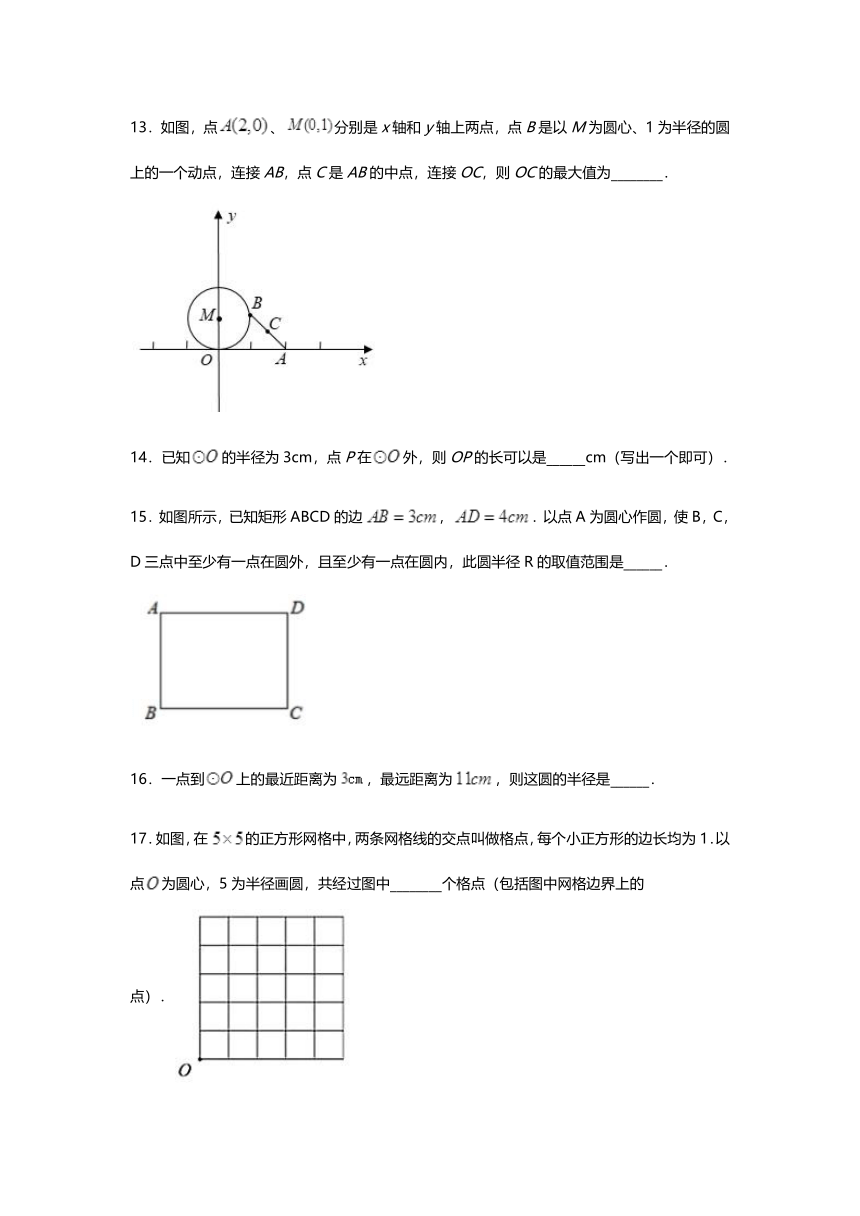
13.如图,点、分别是x轴和y轴上两点,点B是以M为圆心、1为半径的圆上的一个动点,连接AB,点C是AB的中点,连接OC,则OC的最大值为________.
14.已知的半径为3cm,点P在外,则OP的长可以是______cm(写出一个即可).
15.如图所示,已知矩形ABCD的边,.以点A为圆心作圆,使B,C,D三点中至少有一点在圆外,且至少有一点在圆内,此圆半径R的取值范围是______.
16.一点到上的最近距离为,最远距离为,则这圆的半径是______.
17.如图,在的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均为1.以点为圆心,5为半径画圆,共经过图中________个格点(包括图中网格边界上的点).
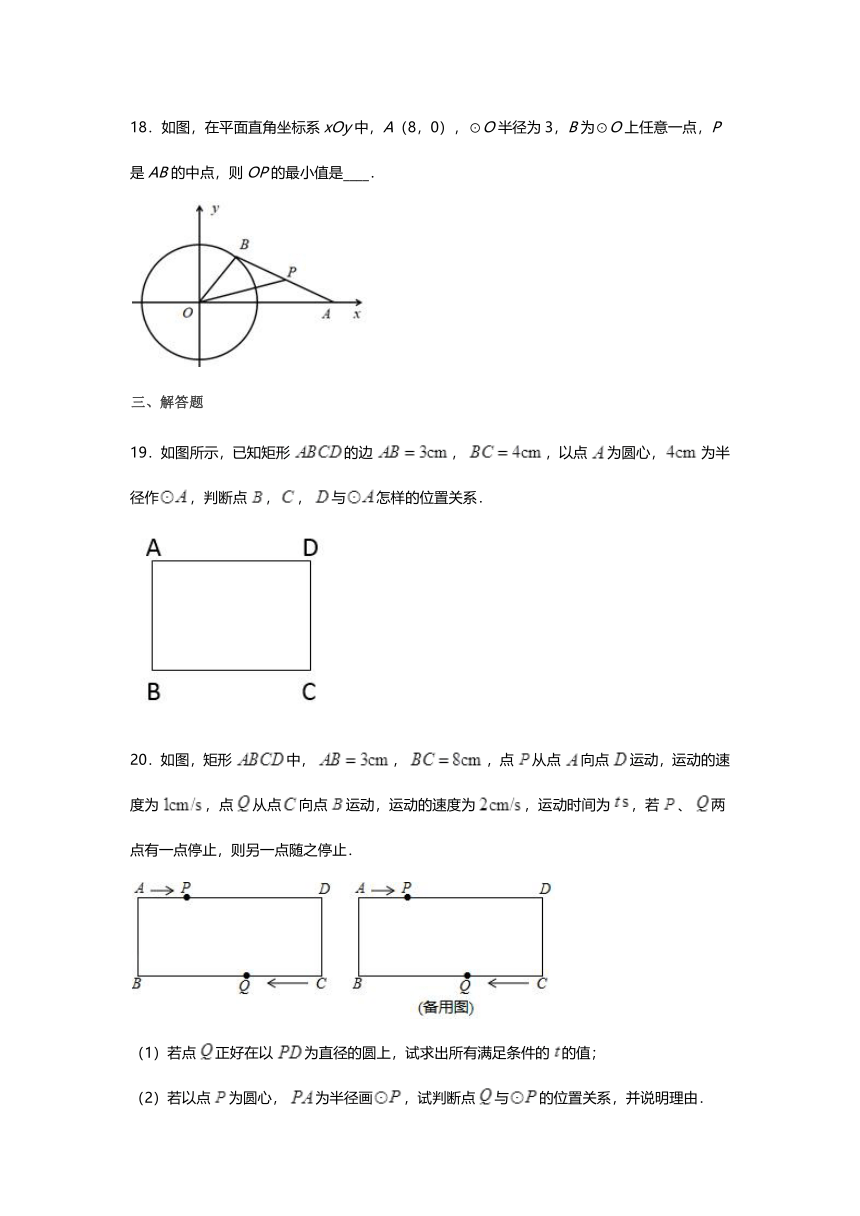
18.如图,在平面直角坐标系xOy中,A(8,0),⊙O半径为3,B为⊙O上任意一点,P是AB的中点,则OP的最小值是____.
三、解答题
19.如图所示,已知矩形的边,,以点为圆心,为半径作,判断点,,与怎样的位置关系.
20.如图,矩形中,,,点从点向点运动,运动的速度为,点从点向点运动,运动的速度为,运动时间为,若、两点有一点停止,则另一点随之停止.
(1)若点正好在以为直径的圆上,试求出所有满足条件的的值;
(2)若以点为圆心,为半径画,试判断点与的位置关系,并说明理由.
21.如图所示,已知△ABC中,∠C=90°,AC=3,BC=4,M为AB的中点.
(1)以C为圆心,3为半径作⊙C,则点A、B、M与⊙C的位置关系如何?
(2)若以C为圆心,作⊙C,使A、M两点在⊙A内且B点在⊙C外,求⊙C的半径r的取值范围.
3.2
圆的对称性
选择题
1.下列说法中,正确的是(
)
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等所对的圆心角相等
2.如图,在⊙O中,∠ABC=60°,则∠AOC等于(? )
A.30°?????B.60°?????C.100°????D.120°
3.下列命题中,正确的有(
)
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
4.下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等。其中是真命题的是(????)
A.?①②????B.?②③????C.?①③????D.?①②③
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,,,则∠DAC的度数是(
)
A.
70°
B.
45°
C.
35°
D.
30°
6.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
A.20°?????B.30°?????C.40°?????D.70°
7.如图所示,在⊙O中,,
∠A=30°,则∠B=( )
A.?150°???B.?75°???C.?60°????D.?15°
8.下列命题中,不正确的是(
)
A.圆是轴对称图形
B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形
D.以上都不对
9.若⊙O内一条弦把圆周分为3∶1的两段弧,且⊙O的半径为R,那么这条弦的长为(
)
A.R
B.2R
C.R
D.R
10..如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x,则x的取值范围是(????
)
A.30≤x≤60???B.30≤x≤90??C.30≤x≤120??D.60≤x≤120
填空题
11.如图,A、B、C、D是⊙上四点,且D是AB的中点,CD交OB于E,,=
度.
12..如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=________.
13.如图,AB是半圆的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为
cm.
14.在同圆中,若,
则AB?________2CD(填>,<,=).
15.如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,A、B、P是⊙O上的点,则tan∠APB=________.
综合题
16.如图,在⊙O中,
AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
17.储油罐截面直径650mm,装入一些油后,若油面宽AB=600mm,求油的最大深度.
18.我们已经知道在⊙O中,如果2∠AOB=∠COD,则CD=2AB,那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
19..如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。
(1)求证:∠DAC=∠BAC;
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。
3.2
圆的对称性
同步测试答案
选择题
1.B
2.D
3.D
4.A
5.C
6.A
7.B
8.C
9.C
10.A
二、填空题
11.800
12.1400
13.2
14.<
15.
(
⌒
⌒
)三、综合题
16.证明:∵AB=CD,
∴
AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
17.200mm
18.解:CD=2AB不成立.理由如下:
取的中点E,连接OE,CE,DE.
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
19.?(1)证明:如解图,连接OC,
则OC=OA,
∴∠BAC=∠OCA,
∵EF切⊙O于点C,
∴OC⊥EF,
∵AD⊥EF,
∴OC∥AD,
∴∠OCA=∠DAC,
∴∠DAC=∠BAC;
(2)解:如解图,连接BC,
∵AB是⊙O的直径,AD⊥EF,
∴∠ACB=∠ADC=90°,
由(Ⅰ)知∠DAC=∠BAC,
∴△ADC∽△ACB,
∴AC2=AD?AB=3×4=12,
∴AC=2,
在Rt△ABC中,cos∠BAC=,
∴∠BAC=30°?.?
?
3.3垂径定理
一.选择题
1.如图,⊙O的半径为3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠P=30°,则弦AB的长为( )
A.2
B.2
C.
D.2
2.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.cm
B.8cm
C.6cm
D.4cm
3.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
4.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17
B.18
C.19
D.20
5.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为( )
A.2
B.2
C.
D.
6.《九章算术》是我国古代著名数学暮作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长.”则CD=( )
A.13寸
B.20寸
C.26寸
D.28寸
7.如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
A.3mm
B.4mm
C.5mm
D.8mm
8.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.
B.
C.
D.
9.如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是上一点,则∠APB的度数为( )
A.30°
B.45°
C.60°
D.75°
10.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
A.3
B.
C.2.5
D.2
11.如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
12.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )
A.5
B.
C.3
D.
13.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4
B.5
C.6
D.6
14.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
A.2
B.4
C.4
D.8
15.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
A.
B.
C.1
D.2
16.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
17.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7
B.17
C.7或17
D.34
18.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EB.若AB=4,CD=1,则EB的长为( )
A.3
B.4
C.5
D.2.5
二.填空题
19.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O半径为
.
20.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为
.
21.如图,AC是⊙O的直径,弦BD⊥AO,垂足为点E,连接BC,过点O作OF⊥BC,垂足为F,若BD=8cm,AE=2cm,则OF的长度是
cm.
22.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为
.
23.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为
.
24.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是
.
25.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有
个.
26.如图,矩形ABCD的边AB过⊙O的圆心,E、F分别为AB、CD与⊙O的交点,若AE=3cm,AD=4cm,DF=5cm,则⊙O的直径等于
.
27.如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是
.
28.王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为
m.
29.蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为
m.
30.某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备
cm内径的管道(内径指内部直径).
三.解答题
31.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
32.如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
(1)试确定所在圆的圆心O;
(2)设△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
33.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
34.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
35.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
36.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
37.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
38.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2),C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为
;
(2)连结AD,CD,求⊙D的半径(结果保留根号).
39.如图为桥洞的形状,其正视图是由和矩形ABCD构成.O点为所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F
)EF为2米.求所在⊙O的半径DO.
40.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F
(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径.
参考答案
一.选择题
1.【解答】解:连接OA,作OC⊥AB于C,则AC=BC,∵OP=4,∠P=30°,∴OC=2,
∴AC==,∴AB=2AC=2,故选:A.
2.【解答】解:如图所示,连接OA.⊙O的直径CD=10cm,则⊙O的半径为5cm,即OA=OC=5,
又∵OM:OC=3:5,所以OM=3,∵AB⊥CD,垂足为M,∴AM=BM,
在Rt△AOM中,AM==4,∴AB=2AM=2×4=8.故选:B.
3.【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,∴BD=AB=×48=24(cm),∵⊙O的直径为52cm,∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),故选:C.
4.【解答】解:连接OP,OQ,分别交AC,BC于H,I,
∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,
∴H、I是AC、BC的中点,∴OH+OI=(AC+BC)=13,
∵MH+NI=AC+BC=13,MP+NQ=7,∴PH+QI=13﹣7=6,
∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,故选:C.
5.【解答】解:如图,连接OD,∵CD⊥OC,∴∠DCO=90°,∴CD==,
当OC的值最小时,CD的值最大,OC⊥AB时,OC最小,此时D、B两点重合,∴CD=CB=AB=2,
即CD的最大值为2,故选:B.
6.【解答】解:连接OA,∵AB⊥CD,且AB=10,∴AE=BE=5,
设圆O的半径OA的长为x寸,则OC=OD=x寸,∵DE=1,∴OE=x﹣1,
在直角三角形AOE中,根据勾股定理得:x2﹣(x﹣1)2=52,化简得:x2﹣x2+2x﹣1=25,
即2x=26,解得:x=13所以CD=26(寸).故选:C.
7.【解答】解:连接OA,∵OD⊥AB,∴AD=AB=4,由勾股定理得,OA==5,故选:C.
8.【解答】解:如图所示,
连接AO,过O作OD⊥AB,交于点D,交弦AB于点E,∵折叠后恰好经过圆心,∴OE=DE,
∵⊙O的半径为4,∴OE=OD=×4=2,∵OD⊥AB,∴AE=AB,
在Rt△AOE中,AE===2.∴AB=2AE=4.故选:A.
9.【解答】解:作半径OC⊥AB于D,连结OA、OB,如图,
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,∴OD=CD,∴OD=OC=OA,∴∠OAD=30°,
又OA=OB,∴∠OBA=30°,∴∠AOB=120°,
∴∠APB=∠AOB=60°.
故选:C.
10.【解答】解:如图:延长CP交⊙O于N,连接DN.∵AB⊥CN,∴CP=PN,∵CM=DM,∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为.故选:C.
11.【解答】解:如图,
连接OA,∵⊙O的直径CD=12cm,∴OD=OA=OC=6,∵OE:OC=1:3,∴OE=2,
∵AB⊥CD,∴AB=2AE,∠OEA=90°,在Rt△OAE中,AE===4,
∴AB=2AE=8cm.故选:D.
12.【解答】解:设⊙O的半径为r,则OA=r,OC=r﹣1,∵OD⊥AB,AB=4,∴AC=AB=2,
在Rt△ACO中,OA2=AC2+OC2,∴r2=22+(r﹣1)2,r=,故选:D.
13.【解答】解:∵OC⊥AB,OC过圆心O点,∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,故选:D.
14.【解答】解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
∵∠AMB=45°,∴∠AOB=2∠AMB=90°,∴△OAB为等腰直角三角形,∴AB=OA=2,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB?CD+AB?CE=AB(CD+CE)=AB?DE=×2×4=4.
故选:C.
15.【解答】解:∵OD⊥AC,AC=2,∴AD=CD=1,∵OD⊥AC,EF⊥AB,∴∠ADO=∠OFE=90°,
∵OE∥AC,∴∠DOE=∠ADO=90°,∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,在△ADO和△OFE中,,∴△ADO≌△OFE(AAS),
∴OF=AD=1,故选:C.
16.【解答】解:连接OA,∵⊙O的直径CD=20,OM:OC=3:5,∴OC=10,OM=6,
∵AB⊥CD,∴AM===8,∴AB=2AM=16.
故选:C.
17.【解答】解:如图,AE=AB=×24=12,CF=CD=×10=5,OE===5,
OF===12,
①当两弦在圆心同侧时,距离=OF﹣OE=12﹣5=7;②当两弦在圆心异侧时,距离=OE+OF=12+5=17.
所以距离为7或17.故选:C.
18.【解答】解:设⊙O的半径为r.∵OD⊥AB,∴AC=BC=2,在Rt△AOC中,∵∠ACO=90°,
∴OA2=OC2+AC2,∴r2=(r﹣1)2+22,∴r=,∴OC=,∵OA=OE,AC=CB,∴BE=2OC=3,
故选:A.
二.填空题
19.【解答】解:连结OC,设⊙O半径为r,则OC=r,OE=r﹣BE=r﹣2,
∵CD⊥AB,∴CE=DE=CD=6,在Rt△OCE中,∵OE2+CE2=OC2,∴(r﹣2)2+62=r2,解得r=10,
即⊙O半径为10.故答案为10.
20.【解答】解:连接OC,
∵CD⊥AB,∴CH=DH=CD=×8=4,∵直径AB=10,∴OC=5,
在Rt△OCH中,OH==3,故答案为:3.
21.【解答】解:连接AB,∵BD⊥AO,∴BE=ED=BD=4,
由勾股定理得,AB==2,∵OF⊥BC,∴CF=FB,又CO=OA,
∴OF=AB=(cm),故答案为:.
22.【解答】解:连接OD,
∵CD⊥AB于点E,直径AB过O,∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,即⊙O的半径为5.故答案为:5.
23.【解答】解:作OH⊥CD于H,连结OC,如图,∵OH⊥CD,∴HC=HD,∵AP=2,BP=6,∴AB=8,
∴OA=4,∴OP=OA﹣AP=2,在Rt△OPH中,∵∠OPH=30°,∴∠POH=60°,∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,∴CH=,
∴CD=2CH=2.故答案为:2
24.【解答】解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.故答案是:121°.
25.【解答】解:∵点A的坐标为(0,1),圆的半径为5,∴点B的坐标为(0,﹣4),
又∵点P的坐标为(0,﹣7),∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,连接BC,在Rt△BCP中,CP==4;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大,此时CD=直径AE=10;
所以,8≤CD≤10,
所以符合的弦有4条,整数值是8(一条弦),9(两条弦),10(一条弦),
综上可得:弦CD长的所有可能的整数值有:8,9,10,共3个,
故答案为:3.
26.【解答】解:连接OF,作FG⊥AB于点G.则EG=DF﹣AE=5﹣3=2cm.设⊙O的半径是R,
则OF=R,OG=R﹣2.在直角△OFG中,OF2=FG2+OG2,即R2=(R﹣2)2+42,
解得:R=5.则直径是10cm.故答案是:10.
27.【解答】解:过点O作OD⊥AB于点D,连接OA,由垂线段最短可知当M于点D重合时OM最短,当OM是半径时最长,∵,⊙O的直径为10,∴OA=5,∵弦AB的长为8,OD⊥AB,∴AD=AB=4,
在Rt△OAD中,OD===3,∴当OM=3时最短,
∴OM长的取值范围是:3≤OM≤5.故答案为:3≤OM≤5.
28.【解答】解:连接OA,∵OD⊥AB,∴AD=AB=3,
在Rt△AOD中,OA2=OD2+AD2,即OC2=(9﹣OC)2+32,解得,OC=5,
故答案为:5.
29.【解答】解:∵CD垂直平分AB,∴AD=8.∴OD==6m,
∴CD=OC﹣OD=10﹣6=4(m).故答案为:4.
30.【解答】解:如图,过O作OC⊥AB于C,连接AO,
∴AC=AB=×60=30,CO=AO﹣10,在Rt△AOC中,AO2=AC2+OC2,AO2=302+(AO﹣10)2,
解得AO=50cm.∴内径为2×50=100cm.故答案为:100.
三.解答题
31.【解答】解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4,
在Rt△AEO中,OE===3,
∴ED=OD﹣OE=5﹣3=2,
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
32.【解答】解:(1)作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)
设半径为r.连接OA,因为BA=AC,故AO⊥BC.
所以:CD=×10=5,AD==.
根据勾股定理,(R﹣)2+52=R2,解得R=.
33.【解答】解:作OP⊥CD于P,连接OD,∴CP=PD,∵AE=1,EB=5,∴AB=6,
∴OE=2,在Rt△OPE中,OP=OE?sin∠DEB=,∴PD==,
∴CD=2PD=2(cm).
34.【解答】解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,∵点C为弧ABD中点,∴=,∴∠ADC=∠DAC=β,∴∠DAB=β﹣α,
连接AD,∵AB为⊙O直径,∴∠ADB=90°,∴α+β=90°,∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),∴∠ABD=2α,∴∠ABD=2∠BDC;
(2)∵CE⊥AB,∴∠ACE+∠CAB=∠ADC+∠BDC=90°,∵∠CAB=∠CDB,∴∠ACE=∠ADC,
∵∠CAE=∠ADC,∴∠ACE=∠CAE,∴AE=CE;
(3)如图2,连接OC,∴∠COB=2∠CAB,∵∠ABD=2∠BDC,∠BDC=∠CAB,∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,∴△OCH∽△ABD,∴,∵OH=5,∴BD=10,
∴AB==26,∴AO=13,∴AH=18,∵△AHE∽△ADB,∴,即=,
∴AE=,∴DE=.
35.【解答】解:这辆卡车能通过厂门.理由如下:
如图M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
则CD=MN=1.6m,AB=2m,
由作法得,CE=DE=0.8m,又∵OC=OA=1m,
在Rt△OCE中,OE===0.6(m),∴CM=2.3+0.6=2.9m>2.5m.
所以这辆卡车能通过厂门.
36.【解答】解:(1)连结OA,由题意得:AD=AB=30(米),OD=(r﹣18)
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,解得,r=34(米);
(2)连结OA′,∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).∴A′B′=32(米).∵A′B′=32>30,
∴不需要采取紧急措施.
37.【解答】解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,∴OF=OE=1,在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,则CD=2DF=2.
38.【解答】解:(1)如图1,∵圆弧经过网格点A(0,2),B(4,2),∴圆心的横坐标为2,
作BC的垂直平分线与AB的垂直平分线交于D,则D(2,﹣2),故答案为:(2,﹣2);
(2)如图2,过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,AE=4,DE=2,
则r==2,所以⊙D的半径为2.
39.【解答】解:∵OE⊥弦CD于点F,CD为8米,EF为2米,∴EO垂直平分CD,DF=4m,FO=DO﹣2,
在Rt△DFO中,DO2=FO2+DF2,则DO2=(DO﹣2)2+42,解得:DO=5;
答:所在⊙O的半径DO为5m.
40.【解答】(1)证明:∵PD∥CB,∴=,∴∠FBC=∠FCB,∴FC=FB.
(2)解:如图:连接OC,设圆的半径为r,在Rt△OCE中,
OC=r,OE=r﹣8,CE=12,∴r2=(r﹣8)2+122,
解方程得:r=13.
所以⊙O的直径为26.
一、单选题
1.⊙O的半径为5,点P到圆心O的距离为4,点P与⊙O的位置关系是
A.无法确定
B.点P在⊙O外
C.点P在⊙O上
D.点P在⊙O内
2.已知,的半径为2,圆心为坐标原点,则点与的位置关系是(???)
A.点在上
B.点在内
C.点在外
D.不确定
3.已知⊙O的半径为10cm,点p到圆心O的距离为8cm,则点p和圆的位置关系(???)
A.点在圆内
B.点在圆外
C.点在圆上
D.无法判断
4.若的半径是,点在内,则的长可能是(???)
A.
B.
C.
D.
5.已知△ABC,以AB为直径作⊙O,∠C=88°,则点C在( )
A.⊙O上
B.⊙O外
C.⊙O
内
D.无法确定
6.点P到圆上各点的最大距离为10cm,最小距离为6cm,则此圆的半径为(???)
A.8cm
B.5cm或3cm
C.8cm或2cm
D.3cm
7.已知⊙O的半径r=3,点P和圆心O之间的距离为d,且方程没有实数根,则点P与⊙O的位置关系是(????)
A.在圆上
B.在圆内
C.在圆外
D.不能确定
8.到圆心的距离不大于半径的点的集合是(?)
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
9.如图,等腰三角形ABC中,AB=AC,AD为底边上的高,BC=6,AC=5,以A为圆心,AD为半径作⊙A,则点C与⊙A的位置关系是( )
A.点C在⊙A内
B.点C在⊙A上
C.点C在⊙A外
D.不能确定
10.点A,B的坐标分别为A?(4,0),B(0,4),点C为坐标平面内一点,BC﹦2,点M为线段AC的中点,连接OM,则OM的最大值为(???)
A.2+1
B.2+2
C.4+1
D.4-2
二、填空题
11.若半径为5,圆心的坐标是,点的坐标是,那么点与的位置关系为点在_________(填“内”,“上”或“外”)
12.已知的半径为6cm,若,则点P与的位置关系是__________.
13.如图,点、分别是x轴和y轴上两点,点B是以M为圆心、1为半径的圆上的一个动点,连接AB,点C是AB的中点,连接OC,则OC的最大值为________.
14.已知的半径为3cm,点P在外,则OP的长可以是______cm(写出一个即可).
15.如图所示,已知矩形ABCD的边,.以点A为圆心作圆,使B,C,D三点中至少有一点在圆外,且至少有一点在圆内,此圆半径R的取值范围是______.
16.一点到上的最近距离为,最远距离为,则这圆的半径是______.
17.如图,在的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均为1.以点为圆心,5为半径画圆,共经过图中________个格点(包括图中网格边界上的点).
18.如图,在平面直角坐标系xOy中,A(8,0),⊙O半径为3,B为⊙O上任意一点,P是AB的中点,则OP的最小值是____.
三、解答题
19.如图所示,已知矩形的边,,以点为圆心,为半径作,判断点,,与怎样的位置关系.
20.如图,矩形中,,,点从点向点运动,运动的速度为,点从点向点运动,运动的速度为,运动时间为,若、两点有一点停止,则另一点随之停止.
(1)若点正好在以为直径的圆上,试求出所有满足条件的的值;
(2)若以点为圆心,为半径画,试判断点与的位置关系,并说明理由.
21.如图所示,已知△ABC中,∠C=90°,AC=3,BC=4,M为AB的中点.
(1)以C为圆心,3为半径作⊙C,则点A、B、M与⊙C的位置关系如何?
(2)若以C为圆心,作⊙C,使A、M两点在⊙A内且B点在⊙C外,求⊙C的半径r的取值范围.
3.2
圆的对称性
选择题
1.下列说法中,正确的是(
)
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等所对的圆心角相等
2.如图,在⊙O中,∠ABC=60°,则∠AOC等于(? )
A.30°?????B.60°?????C.100°????D.120°
3.下列命题中,正确的有(
)
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
4.下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等。其中是真命题的是(????)
A.?①②????B.?②③????C.?①③????D.?①②③
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,,,则∠DAC的度数是(
)
A.
70°
B.
45°
C.
35°
D.
30°
6.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
A.20°?????B.30°?????C.40°?????D.70°
7.如图所示,在⊙O中,,
∠A=30°,则∠B=( )
A.?150°???B.?75°???C.?60°????D.?15°
8.下列命题中,不正确的是(
)
A.圆是轴对称图形
B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形
D.以上都不对
9.若⊙O内一条弦把圆周分为3∶1的两段弧,且⊙O的半径为R,那么这条弦的长为(
)
A.R
B.2R
C.R
D.R
10..如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x,则x的取值范围是(????
)
A.30≤x≤60???B.30≤x≤90??C.30≤x≤120??D.60≤x≤120
填空题
11.如图,A、B、C、D是⊙上四点,且D是AB的中点,CD交OB于E,,=
度.
12..如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=________.
13.如图,AB是半圆的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为
cm.
14.在同圆中,若,
则AB?________2CD(填>,<,=).
15.如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,A、B、P是⊙O上的点,则tan∠APB=________.
综合题
16.如图,在⊙O中,
AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
17.储油罐截面直径650mm,装入一些油后,若油面宽AB=600mm,求油的最大深度.
18.我们已经知道在⊙O中,如果2∠AOB=∠COD,则CD=2AB,那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
19..如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。
(1)求证:∠DAC=∠BAC;
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。
3.2
圆的对称性
同步测试答案
选择题
1.B
2.D
3.D
4.A
5.C
6.A
7.B
8.C
9.C
10.A
二、填空题
11.800
12.1400
13.2
14.<
15.
(
⌒
⌒
)三、综合题
16.证明:∵AB=CD,
∴
AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
17.200mm
18.解:CD=2AB不成立.理由如下:
取的中点E,连接OE,CE,DE.
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
19.?(1)证明:如解图,连接OC,
则OC=OA,
∴∠BAC=∠OCA,
∵EF切⊙O于点C,
∴OC⊥EF,
∵AD⊥EF,
∴OC∥AD,
∴∠OCA=∠DAC,
∴∠DAC=∠BAC;
(2)解:如解图,连接BC,
∵AB是⊙O的直径,AD⊥EF,
∴∠ACB=∠ADC=90°,
由(Ⅰ)知∠DAC=∠BAC,
∴△ADC∽△ACB,
∴AC2=AD?AB=3×4=12,
∴AC=2,
在Rt△ABC中,cos∠BAC=,
∴∠BAC=30°?.?
?
3.3垂径定理
一.选择题
1.如图,⊙O的半径为3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠P=30°,则弦AB的长为( )
A.2
B.2
C.
D.2
2.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.cm
B.8cm
C.6cm
D.4cm
3.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
4.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17
B.18
C.19
D.20
5.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为( )
A.2
B.2
C.
D.
6.《九章算术》是我国古代著名数学暮作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长.”则CD=( )
A.13寸
B.20寸
C.26寸
D.28寸
7.如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
A.3mm
B.4mm
C.5mm
D.8mm
8.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.
B.
C.
D.
9.如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是上一点,则∠APB的度数为( )
A.30°
B.45°
C.60°
D.75°
10.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
A.3
B.
C.2.5
D.2
11.如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
12.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )
A.5
B.
C.3
D.
13.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4
B.5
C.6
D.6
14.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
A.2
B.4
C.4
D.8
15.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
A.
B.
C.1
D.2
16.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
17.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7
B.17
C.7或17
D.34
18.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EB.若AB=4,CD=1,则EB的长为( )
A.3
B.4
C.5
D.2.5
二.填空题
19.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O半径为
.
20.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为
.
21.如图,AC是⊙O的直径,弦BD⊥AO,垂足为点E,连接BC,过点O作OF⊥BC,垂足为F,若BD=8cm,AE=2cm,则OF的长度是
cm.
22.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为
.
23.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为
.
24.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是
.
25.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有
个.
26.如图,矩形ABCD的边AB过⊙O的圆心,E、F分别为AB、CD与⊙O的交点,若AE=3cm,AD=4cm,DF=5cm,则⊙O的直径等于
.
27.如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是
.
28.王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为
m.
29.蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为
m.
30.某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备
cm内径的管道(内径指内部直径).
三.解答题
31.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
32.如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
(1)试确定所在圆的圆心O;
(2)设△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
33.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
34.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
35.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.
36.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
37.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
38.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2),C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为
;
(2)连结AD,CD,求⊙D的半径(结果保留根号).
39.如图为桥洞的形状,其正视图是由和矩形ABCD构成.O点为所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F
)EF为2米.求所在⊙O的半径DO.
40.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F
(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径.
参考答案
一.选择题
1.【解答】解:连接OA,作OC⊥AB于C,则AC=BC,∵OP=4,∠P=30°,∴OC=2,
∴AC==,∴AB=2AC=2,故选:A.
2.【解答】解:如图所示,连接OA.⊙O的直径CD=10cm,则⊙O的半径为5cm,即OA=OC=5,
又∵OM:OC=3:5,所以OM=3,∵AB⊥CD,垂足为M,∴AM=BM,
在Rt△AOM中,AM==4,∴AB=2AM=2×4=8.故选:B.
3.【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,∴BD=AB=×48=24(cm),∵⊙O的直径为52cm,∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),故选:C.
4.【解答】解:连接OP,OQ,分别交AC,BC于H,I,
∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,
∴H、I是AC、BC的中点,∴OH+OI=(AC+BC)=13,
∵MH+NI=AC+BC=13,MP+NQ=7,∴PH+QI=13﹣7=6,
∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,故选:C.
5.【解答】解:如图,连接OD,∵CD⊥OC,∴∠DCO=90°,∴CD==,
当OC的值最小时,CD的值最大,OC⊥AB时,OC最小,此时D、B两点重合,∴CD=CB=AB=2,
即CD的最大值为2,故选:B.
6.【解答】解:连接OA,∵AB⊥CD,且AB=10,∴AE=BE=5,
设圆O的半径OA的长为x寸,则OC=OD=x寸,∵DE=1,∴OE=x﹣1,
在直角三角形AOE中,根据勾股定理得:x2﹣(x﹣1)2=52,化简得:x2﹣x2+2x﹣1=25,
即2x=26,解得:x=13所以CD=26(寸).故选:C.
7.【解答】解:连接OA,∵OD⊥AB,∴AD=AB=4,由勾股定理得,OA==5,故选:C.
8.【解答】解:如图所示,
连接AO,过O作OD⊥AB,交于点D,交弦AB于点E,∵折叠后恰好经过圆心,∴OE=DE,
∵⊙O的半径为4,∴OE=OD=×4=2,∵OD⊥AB,∴AE=AB,
在Rt△AOE中,AE===2.∴AB=2AE=4.故选:A.
9.【解答】解:作半径OC⊥AB于D,连结OA、OB,如图,
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,∴OD=CD,∴OD=OC=OA,∴∠OAD=30°,
又OA=OB,∴∠OBA=30°,∴∠AOB=120°,
∴∠APB=∠AOB=60°.
故选:C.
10.【解答】解:如图:延长CP交⊙O于N,连接DN.∵AB⊥CN,∴CP=PN,∵CM=DM,∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为.故选:C.
11.【解答】解:如图,
连接OA,∵⊙O的直径CD=12cm,∴OD=OA=OC=6,∵OE:OC=1:3,∴OE=2,
∵AB⊥CD,∴AB=2AE,∠OEA=90°,在Rt△OAE中,AE===4,
∴AB=2AE=8cm.故选:D.
12.【解答】解:设⊙O的半径为r,则OA=r,OC=r﹣1,∵OD⊥AB,AB=4,∴AC=AB=2,
在Rt△ACO中,OA2=AC2+OC2,∴r2=22+(r﹣1)2,r=,故选:D.
13.【解答】解:∵OC⊥AB,OC过圆心O点,∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,故选:D.
14.【解答】解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
∵∠AMB=45°,∴∠AOB=2∠AMB=90°,∴△OAB为等腰直角三角形,∴AB=OA=2,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB?CD+AB?CE=AB(CD+CE)=AB?DE=×2×4=4.
故选:C.
15.【解答】解:∵OD⊥AC,AC=2,∴AD=CD=1,∵OD⊥AC,EF⊥AB,∴∠ADO=∠OFE=90°,
∵OE∥AC,∴∠DOE=∠ADO=90°,∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,在△ADO和△OFE中,,∴△ADO≌△OFE(AAS),
∴OF=AD=1,故选:C.
16.【解答】解:连接OA,∵⊙O的直径CD=20,OM:OC=3:5,∴OC=10,OM=6,
∵AB⊥CD,∴AM===8,∴AB=2AM=16.
故选:C.
17.【解答】解:如图,AE=AB=×24=12,CF=CD=×10=5,OE===5,
OF===12,
①当两弦在圆心同侧时,距离=OF﹣OE=12﹣5=7;②当两弦在圆心异侧时,距离=OE+OF=12+5=17.
所以距离为7或17.故选:C.
18.【解答】解:设⊙O的半径为r.∵OD⊥AB,∴AC=BC=2,在Rt△AOC中,∵∠ACO=90°,
∴OA2=OC2+AC2,∴r2=(r﹣1)2+22,∴r=,∴OC=,∵OA=OE,AC=CB,∴BE=2OC=3,
故选:A.
二.填空题
19.【解答】解:连结OC,设⊙O半径为r,则OC=r,OE=r﹣BE=r﹣2,
∵CD⊥AB,∴CE=DE=CD=6,在Rt△OCE中,∵OE2+CE2=OC2,∴(r﹣2)2+62=r2,解得r=10,
即⊙O半径为10.故答案为10.
20.【解答】解:连接OC,
∵CD⊥AB,∴CH=DH=CD=×8=4,∵直径AB=10,∴OC=5,
在Rt△OCH中,OH==3,故答案为:3.
21.【解答】解:连接AB,∵BD⊥AO,∴BE=ED=BD=4,
由勾股定理得,AB==2,∵OF⊥BC,∴CF=FB,又CO=OA,
∴OF=AB=(cm),故答案为:.
22.【解答】解:连接OD,
∵CD⊥AB于点E,直径AB过O,∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,即⊙O的半径为5.故答案为:5.
23.【解答】解:作OH⊥CD于H,连结OC,如图,∵OH⊥CD,∴HC=HD,∵AP=2,BP=6,∴AB=8,
∴OA=4,∴OP=OA﹣AP=2,在Rt△OPH中,∵∠OPH=30°,∴∠POH=60°,∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,∴CH=,
∴CD=2CH=2.故答案为:2
24.【解答】解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.故答案是:121°.
25.【解答】解:∵点A的坐标为(0,1),圆的半径为5,∴点B的坐标为(0,﹣4),
又∵点P的坐标为(0,﹣7),∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,连接BC,在Rt△BCP中,CP==4;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大,此时CD=直径AE=10;
所以,8≤CD≤10,
所以符合的弦有4条,整数值是8(一条弦),9(两条弦),10(一条弦),
综上可得:弦CD长的所有可能的整数值有:8,9,10,共3个,
故答案为:3.
26.【解答】解:连接OF,作FG⊥AB于点G.则EG=DF﹣AE=5﹣3=2cm.设⊙O的半径是R,
则OF=R,OG=R﹣2.在直角△OFG中,OF2=FG2+OG2,即R2=(R﹣2)2+42,
解得:R=5.则直径是10cm.故答案是:10.
27.【解答】解:过点O作OD⊥AB于点D,连接OA,由垂线段最短可知当M于点D重合时OM最短,当OM是半径时最长,∵,⊙O的直径为10,∴OA=5,∵弦AB的长为8,OD⊥AB,∴AD=AB=4,
在Rt△OAD中,OD===3,∴当OM=3时最短,
∴OM长的取值范围是:3≤OM≤5.故答案为:3≤OM≤5.
28.【解答】解:连接OA,∵OD⊥AB,∴AD=AB=3,
在Rt△AOD中,OA2=OD2+AD2,即OC2=(9﹣OC)2+32,解得,OC=5,
故答案为:5.
29.【解答】解:∵CD垂直平分AB,∴AD=8.∴OD==6m,
∴CD=OC﹣OD=10﹣6=4(m).故答案为:4.
30.【解答】解:如图,过O作OC⊥AB于C,连接AO,
∴AC=AB=×60=30,CO=AO﹣10,在Rt△AOC中,AO2=AC2+OC2,AO2=302+(AO﹣10)2,
解得AO=50cm.∴内径为2×50=100cm.故答案为:100.
三.解答题
31.【解答】解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4,
在Rt△AEO中,OE===3,
∴ED=OD﹣OE=5﹣3=2,
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
32.【解答】解:(1)作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)
设半径为r.连接OA,因为BA=AC,故AO⊥BC.
所以:CD=×10=5,AD==.
根据勾股定理,(R﹣)2+52=R2,解得R=.
33.【解答】解:作OP⊥CD于P,连接OD,∴CP=PD,∵AE=1,EB=5,∴AB=6,
∴OE=2,在Rt△OPE中,OP=OE?sin∠DEB=,∴PD==,
∴CD=2PD=2(cm).
34.【解答】解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,∵点C为弧ABD中点,∴=,∴∠ADC=∠DAC=β,∴∠DAB=β﹣α,
连接AD,∵AB为⊙O直径,∴∠ADB=90°,∴α+β=90°,∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),∴∠ABD=2α,∴∠ABD=2∠BDC;
(2)∵CE⊥AB,∴∠ACE+∠CAB=∠ADC+∠BDC=90°,∵∠CAB=∠CDB,∴∠ACE=∠ADC,
∵∠CAE=∠ADC,∴∠ACE=∠CAE,∴AE=CE;
(3)如图2,连接OC,∴∠COB=2∠CAB,∵∠ABD=2∠BDC,∠BDC=∠CAB,∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,∴△OCH∽△ABD,∴,∵OH=5,∴BD=10,
∴AB==26,∴AO=13,∴AH=18,∵△AHE∽△ADB,∴,即=,
∴AE=,∴DE=.
35.【解答】解:这辆卡车能通过厂门.理由如下:
如图M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
则CD=MN=1.6m,AB=2m,
由作法得,CE=DE=0.8m,又∵OC=OA=1m,
在Rt△OCE中,OE===0.6(m),∴CM=2.3+0.6=2.9m>2.5m.
所以这辆卡车能通过厂门.
36.【解答】解:(1)连结OA,由题意得:AD=AB=30(米),OD=(r﹣18)
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,解得,r=34(米);
(2)连结OA′,∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).∴A′B′=32(米).∵A′B′=32>30,
∴不需要采取紧急措施.
37.【解答】解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,∴OF=OE=1,在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,则CD=2DF=2.
38.【解答】解:(1)如图1,∵圆弧经过网格点A(0,2),B(4,2),∴圆心的横坐标为2,
作BC的垂直平分线与AB的垂直平分线交于D,则D(2,﹣2),故答案为:(2,﹣2);
(2)如图2,过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,AE=4,DE=2,
则r==2,所以⊙D的半径为2.
39.【解答】解:∵OE⊥弦CD于点F,CD为8米,EF为2米,∴EO垂直平分CD,DF=4m,FO=DO﹣2,
在Rt△DFO中,DO2=FO2+DF2,则DO2=(DO﹣2)2+42,解得:DO=5;
答:所在⊙O的半径DO为5m.
40.【解答】(1)证明:∵PD∥CB,∴=,∴∠FBC=∠FCB,∴FC=FB.
(2)解:如图:连接OC,设圆的半径为r,在Rt△OCE中,
OC=r,OE=r﹣8,CE=12,∴r2=(r﹣8)2+122,
解方程得:r=13.
所以⊙O的直径为26.
