人教A版必修三1.1算法与程序框图(81张PPT)
文档属性
| 名称 | 人教A版必修三1.1算法与程序框图(81张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览











文档简介
1.1算法与程序框图
1.1.1算法的概念
1.1.1 算法的概念
学习目标:
通过分析具体问题过程与步骤,体会算法的思想,了解算法的含义,能用自然语言描述解决具体问题的算法.
学习重点(难点):
通过实例体会算法思想,初步理解算法的含义.
问题1:请你写出解二元一次方程组的详细求解过程.
①
②
第一步:②-①×2得: 5y=3 ③
第二步: 解③得:
第三步: 将 代入①,解得 .
对于一般的二元一次方程组
其中 也可以按照上述步骤求解.
这些步骤就构成了解二元一次方程组的算法,我们可以根据这一算法编制计算机程序,让计算机来解二元一次方程组.
算法的概念与特征:
算法(algorithm)这个词出现于12世纪,指的是用阿拉伯数字进行算术运算的过程.
在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
说明:
(1)事实上算法并没有精确化的定义.
(2)算法虽然没有一个明确的定义,但其特点是鲜明的,不仅要注意算法的程序性、有限性、构造性、精确性的特点,还应该充分理解算法问题的指向性,即算法往往指向解决某一类问题,泛泛地谈算法是没有意义的。
算法学的发展
随着科学技术的日新月异,算法学也得到了前所未有的发展,现在已经发展到了各个领域.有遗传算法,排序算法,加密算法,蚁群算法等,与生物学,计算机科学等有着很广泛的联系,尤其是在现在的航空航天中,更是有着更广泛的应用.
很多复杂的运算都是借助计算机和算法来完成的,在高端科学技术中有着很重要的地位.
例1:
(1)设计一个算法,判断7是否为质数;
(2)设计一个算法,判断35是否为质数。
问题:任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定.
分析:请回顾这个问题的解题过程.
算法分析:
第一步:判断n是否等于2.
若n=2,则n是质数;
若n>2,则执行第二步.
第二步:依次检验2~(n-1)这些整数是不是n的因素,即是不是整除n的数.若有这样的数,则n不是质数;若没有这样的数,则n是质数.
说明:用语言描述一个算法,最便捷的方式就是按解决问题的步骤进行描述.每一步做一件事情.
问题:
设计一个算法,判断整数n(n>2)是否为质数.
第二步:令i=2.
第三步:用i除n,得到余数r
第一步:给定大于2的整数n;
第四步:判断“r=0”是否成立,若是,则n不是质数,结束算法;否则,将i的值增加1,仍用i表示
第五步:判断“i>(n-1)”是否成立,若是,则n是质数,结束算法;否则,返回第三步。
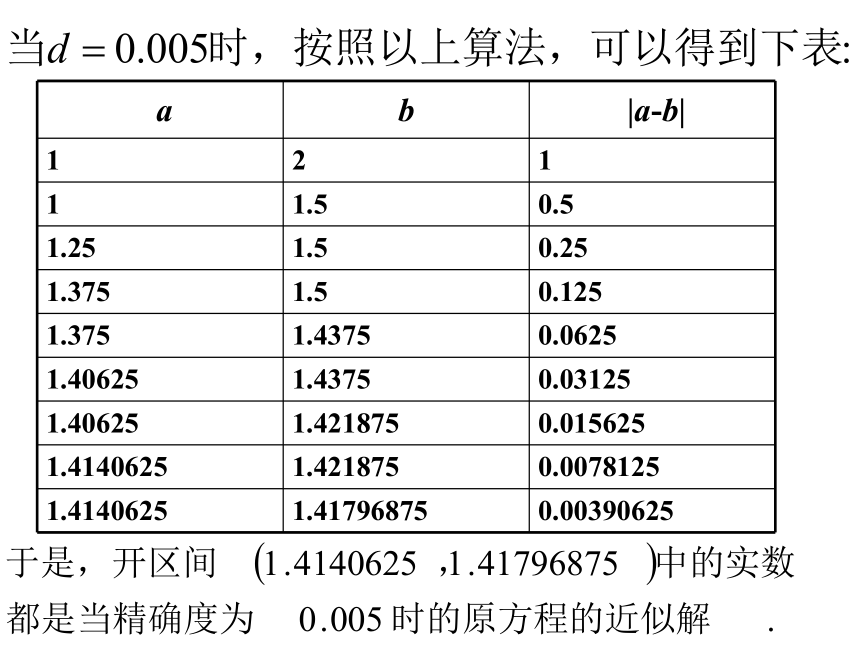
例2:用二分法设计一个求方程x2-2=0的近似根的算法.
算法分析:
设所求近似根与精确解的差的绝对值不超过ε=0.005.
例2.用二分法设计一个求方程x2-2=0是近似根的算法。
算法分析:假设精确度为0.005
第一步:令f(x)=x2-2,因为f (1)<0,f (2)>0,所以设a=1,b=2;
第二步:令 ,判断f (m)是否为0,若是,则m为所求;
若否,则继续判断f (a)·f (m)大于0还是小于0;
a
b
|a-b|
1
2
1
1
1.5
0.5
1.25
1.5
0.25
1.375
1.5
0.125
1.375
1.4375
0.0625
1.40625
1.4375
0.03125
1.40625
1.421875
0.015625
1.4140625
1.421875
0.0078125
1.4140625
1.41796875
0.00390625
点评: (1)上述算法也是求 的近似值的算法.
(2)与一般的解决问题的过程比较,算法有以下特征:
①设计一个具体问题的算法时,与过去熟悉地解数学题的过程有直接的联系,但这个过程必须被分解成若干个明确的步骤,而且这些步骤必须是有效的.
②算法要“面面俱到”,不能省略任何一个细小的步骤,只有这样,才能在人设计出算法后,把具体的执行过程交给计算机完成.
计算机解决任何问题都要依赖于算法.只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”准确地描述出来,计算机才能够解决问题.
例3.试给出一个判断一元二次方程ax2+bx+c=0解的个数的算法.
算法:
第一步:输入a、b、c的值.
第二步:计算? =b2-4ac的值.
第三步:若?>0,则原方程有两个不等的实根;
若?=0,则原方程只有一个实根;
若?<0,则原方程无实根.
第四步:输出结果.
小结:
1、算法:解决问题的过程或步骤;
2、算法的特点:
(1)有限性;
(2)确定性;
(3)可行性;
(4)不唯一性.
作业:
课堂练习:P5 练习1、2
课外作业:P20 习题1.1 A组 1、2
(只需用自然语言写出算法步骤)
练习一:任意给定一个正实数,设计一个算法求以这个数为半径的圆的面积.
算法分析:
第一步:输入任意一个正实数r;
第二步:计算以r为半径的圆的面积S=πr2;
第三步:输出圆的面积.
练习二:任意给定一个大于1的正整数n,设计一个算法求出n的所有因数.
算法分析:
第一步:依次从2~(n-1)为除数去除n,判断余数是否为0,若是,则是n的因数;若不是,则不是n的因数.
第二步:在n的因数中加入1和n;
第三步:输出n的所有因数.
练习三:为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m3的部分,每立方米收费1.5元,并加收0.4元的城市污水处理费,请你写出某户居民每月应交纳的水费y(元)与用水量x(m3)之间的函数关系,然后设计一个求该函数值的算法.
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
求该函数值的算法分析:
第一步:输入每月用水量x;
第二步:判断x是否不超过7.若是,则y=1.2x;若否,则y=1.9x-4.9.
第三步:输出应交纳的水费y.
1.1.2 程序框图
学习目标:(1)在具体问题的解决过程中,掌握基本的程序框图的画法,理解程序框图的三种基本逻辑结构---顺序结构、条件结构、循环结构。
(2)通过模仿、操作、探索,经历通过设计程序框图表达解决问题的算法的过程。
学习重点:通过模仿、操作、探索,经历通过设计程序框图表达求解问题的过程,在具体问题解决过程中,理解程序框图的三种基本逻辑结构.
学习难点:用程序框图清晰表达含有循环结构的算法.
例1:任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定.
算法分析:
第一步:判断n是否等于2.
若n=2,则n是质数;
若n>2,则执行第二步.
第二步:依次检验2~(n-1)这些整数是不是n的因素,即是不是整除n的数.若有这样的数,则n不是质数;若没有这样的数,则n是质数.
从上节课我们知道:算法可以用自然语言来描述.如例1
为了使算法的程序或步骤表达得更为直观,我们更经常地用图形方式来表示它.
开始
输入n
i=2
求n除以i的余数r
i的值增加1仍用i表示
i≥n或r=0?
n不是质数
结束
是
否
是
n是质数
否
r=0?
设n是一个大于2的整数.
一般用i=i+1表示.
i=i+1
说明:i表示从2~(n-1)的所有正整数,用以判断例1步骤2是否终止,i是一个计数变量,有了这个变量,算法才能依次执行.逐步考察从2~(n-1)的所有正整数中是否有n的因数存在.
思考?通过上述算法的两种不同表达方式的比较,你觉得用程序框图来表达算法有哪些特点?
用程序框图表示的算法更加简练,直观,流向清楚.
程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
通常,程序框图由程序框和流程线组成.
一个或几个程序框的组合表示算法中的一个步骤;
流程线是方向箭头,按照算法进行的顺序将程序框连接起来.
1、程序框图
基本的程序框和它们各自表示的功能如下:
图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不”成立时标明“否”或“N”.
判断框
赋值、计算
流程线
连接程序框
连接点
连接程序框图的两部分
开始
输入n
i=2
求n除以i的余数r
i=i+1
i≥n或r=0?
n不是质数
结束
是
否
是
n是质数
否
r=0?
顺序结构
用程序框图来表示算法,有三种不同的基本逻辑结构:
条件结构
循环结构
程序框图的三种基本的逻辑结构
顺序结构
条件结构
循环结构
2、算法的基本逻辑结构:
输入n
i=2
顺序结构
是
n不是质数
n是质数
否
r=0?
条件结构
求n除以i的余数r
i=i+1
i≥n或r=0?
是
否
循环结构
(1)顺序结构-----是由若干个依次执行的处理步骤组成的.这是任何一个算法都离不开的基本结构.
思考?你能说出这三种基本逻辑结构的特点吗?条件结构与循环结构有什么区别和联系?
顺序结构可以用程序
框图表示为
步骤n
步骤n+1
已知三角形三边长分别为a,b,c,则三角形的面积为
其中
这个公式被称为海伦—秦九韶公式.
例3、已知一个三角形的三边边长分别为2,3,4,利用海伦-秦九韶公式设计一个算法,求出它的面积,画出算法的程序框图.
算法分析:
第一步:计算p的值.
第二步:由海伦-秦九韶公式求出三角形的面积S.
第三步:输出S的值.
程序框图:
开始
输出S
结束
画出:已知三角形的三边长a,b,c,求它的面积的程序框图.
开始
输出S
结束
输入a,b,c
(2)条件结构---在一个算法中,经常会遇到一些条件的判断,算法的流向根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.
常见的条件结构可以用程序框图表示为下面两种形式:
满足条件?
是
步骤A
否
步骤B
满足条件?
是
步骤A
否
例4、任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在.画出这个算法的程序框图.
算法分析:
第一步:输入3个正实数a,b,c;
第二步:判断a+b>c,a+c>b,b+c>a是否同时成立,若是,则能组成三角形;若否,则组不成三角形.
程序框图:
开始
输入a,b,c
a+b>c,a+c>b,b+c>a是否
同时成立?
是
存在这样的
三角形
不存在这样的
三角形
否
结束
补例、为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m3的部分,每立方米收费1.5元,并加收0.4元的城市污水处理费,请你写出某户居民每月应交纳的水费y(元)与用水量x(m3)之间的函数关系,然后设计一个求该函数值的算法,并画出程序框图.
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
算法分析:
第一步:输入每月用水量x;
第二步:判断x是否不超过7.若是,则y=1.2x;若否,则y=1.9x-4.9.
第三步:输出应交纳的水费y.
开始
输入x
0是
y=1.2x
否
y=1.9x-4.9
输出y
结束
程序框图
补例、画程序框图,对于输入的x值,输出相应的y值.
开始
程序框图
x<0?
是
y=0
否
0≤x<1?
是
y=1
否
y=x
输出y
结束
输入x
是
例5.设计一个求任意数的绝对值的算法,并画出程序框图.
算法分析:
第一步:输入数x;
第二步:判断x≥0是否成立?若是,则|x|=x;若否,则|x|=-x.
程序框图:
开始
输入x
x≥0?
输出x
否
输出-x
结束
算法分析:
解决这一问题的算法步骤如下:
开始
程序框图
输入a,b,c
结束
是
是
否
否
输出“方程没
有实数根”
作业:
课本P20页练习,
P21页A组T1;
(画出程序框图)
(3)循环结构---在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一步骤的情况,这就是循环结构.
反复执行的步骤称为循环体.
注意:循环结构不能是永无终止的“死循环”,一定要在某个条件下终止循环,这就需要条件结构来作出判断,因此,循环结构中一定包含条件结构.
说明:(1)一般地,循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,同时它的取值还用于判断循环是否终止,累加变量用于输出结果.累加变量和计数变量一般是同步执行的,累加一次,记数一次.
(2)循环结构分为两种------当型和直到型.
当型循环在每次执行循环体前对循环条件进行判断,当条件满足时执行循环体,不满足则停止;(当条件满足时反复执行循环体)
直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.(反复执行循环体,直到条件满足)
(2)循环结构分为两种------当型和直到型.
直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.(反复执行循环体,直到条件满足)
循环体
满足条件?
否
是
(2)循环结构分为两种------当型和直到型.
当型循环在每次执行循环体前对循环条件进行判断,当条件满足时执行循环体,不满足则停止;(当条件满足时反复执行循环体)
循环体
满足条件?
否
是
例6、设计一个计算1+2+3+……+100的值的算法,并画出程序框图.
算法分析:
第1步:0+1=1;
第2步:1+2=3;
第3步:3+3=6;
第4步:6+4=10
…………
第100步:4950+100=5050.
第(i-1)步的结果+i=第i步的结果
各步骤有共同的结构:
为了方便有效地表示上述过程,我们引进一个累加变量S来表示每一步的计算结果,从而把第i步表示为 S=S+i
S的初始值为0,i依次取1,2,…,100,
由于i同时记录了循环的次数,所以i称为计数变量.
程序框图:
开始
i=1
S=0
S=S+i
i=i+1
i>100?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤100?
是
S=S+i
i=i+1
否
输出S
结束
当型循环结构
思考?(P15)
程序框图:
开始
i=1
S=0
S=S+i
i=i+1
i>n?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤n?
是
S=S+i
i=i+1
否
输出S
结束
当型循环结构
输入n
输入n
例7、某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.
算法分析:
先写出解决本例的算法步骤:
第一步,输入2005年的年生产总值.
第二步,计算下一年的年生产总值.
第三步,判断所得的结果是否大于300.若是,则输出该年的年份;否则,返回第二步.
由于“第二步”是重复操作的步骤,所以本例可以用循环结构来实现.我们按照“确定循环体”“初始化变量”“设定循环控制条件”的顺序来构造循环结构.
程序框图:
开始
n=2005
a=200
t=0.05a
a=a+t
a>300?
是
结束
直到型循环结构
n=n+1
输出n
否
3、程序框图的画法:
在用自然语言表述一个算法后,可以画出程序框图,用顺序结构、条件结构和循环结构来表示这个算法.这样表示的算法清楚、简练,便于阅读和交流.
若是,则m
为所求;
探究:画出用二分法求方程x2-2=0的近似根(精确度为0.005)的程序框图.
算法分析:
第一步:令f(x)=x2-2.
因为f(1)<0,f(2)>0,
所以设a=1,b=2.
第二步:令
判断f(m)是否为0.
若否,则继续判断f(a) f(m)大于0还是小于0.
第三步:若f(a) f(m)>0,则令a=m;否则,令b=m.
第四步:判断|a-b|<ε是否成立?若是,则a或b为满足条件的近似根;若否,则返回第二步.
(1)算法步骤中的“第一步”“第二步”和“第三步”可以用顺序结构来表示(图1.1-17)
图1.1-17
f(x)=x2-2
输入精确度d
和初始值a,b
b=m
f(a) f(m)<0?
是
a=m
否
图1.1-18
是
第三步
第四步
图1.1-19
否
(4)将各步骤的程序框图连接起来,并画出“开始”与“结束”两个终端框,就得到了表示整个算法的程序框图.
从以上过程可以看出,设计一个算法的程序框图通常要经过以下步骤:
第一步,用自然语言表述算法步骤.
第二步,确定每一个算法步骤所包含的逻辑结构,并用相应的程序框图表示,得到该步骤的程序框图.
第三步,将所有步骤的程序框图用流程线连接起来,并加上终端框,得到表示整个算法的程序框图.
是
是
否
f(a) f(m)>0?
程序框图
开始
f(x)=x2-2
输入误差ε
和初值a,b
a=m
否
b=m
|a-b|<ε或f(m)=0?
输出m
结束
否
是
是
否
f(a) f(m)>0?
程序框图
开始
f(x)=x2-2
输入误差ε
和初值a,b
f(m)=0?
a=m
否
b=m
|a-b|<ε?
1
2
2
输出a和b
结束
输出m
3
1
3
是
课堂小结
本节主要讲述了程序框图的基本知识:包括常用的图形符号、算法的基本逻辑结构.
算法的基本逻辑结构有三种,即顺序结构、条件结构和循环结构.
其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,它们共同构成了算法的基本结构,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达.
作业:
课本P20 A组2、3.
习题练习
是
1.(P20页A组T3)某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元。设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图。
程序框图:
开始
输入x
x>3?
否
结束
输入y
y=5
y=1.2x+1.4
是
2.(P50页A组T3)某市固定电话(市话)的收费标准为:3分钟之内(包括3分钟)收取0.30元;超过3分钟,每分钟(不足一分钟,按一分钟计算)按0.10元收费。设计一个算法,根据通话时间计算话费。
程序框图:
开始
输入t
0否
结束
输出y
y=0.3
y=0.1t
3.P50页A组T1(1)画程序框图,对于输入的x值,输出相应的y值:
开始
程序框图
x<0?
是
y=0
否
0≤x<1?
是
y=1
否
y=x
输出y
结束
输入x
4.P50页A组T1(2)画程序框图,对于输入的x值,输出相应的y值:
开始
程序框图
x<0?
是
y=(x+2)2
否
x=0?
是
y=4
否
输出y
结束
输入x
y=(x-2)2
开始
i=1
S=0
S=S+i2
i=i+1
i>100?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤100?
是
S=S+i2
i=i+1
否
输出S
结束
当型循环结构
5.P20页A组T2.
开始
i=1
S=0
S=S+
i=i+1
i>n?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤n?
是
S=S+
i=i+1
否
输出S
结束
当型循环结构
6.P50页A组T4.
输入n
输入n
7.(P20BT2).某高中男子体育小组的50m跑成绩(单位:s)为: 6.4, 6.5, 7.0, 6.8, 7.1, 7.3, 6.9, 7.4, 7.5.
设计一个算法,从这些成绩中搜出小于6.8s的成绩.
算法分析:
第一步:把计数变量n的初值设为1.
第二步:输入一个成绩r,判断r与6.8的大小.若r≥6.8,则执行下一步;若r<6.8,则输出r,并执行下一步.
第三步:使计数变量n的值增加1.
第四步:判断计数变量n与成绩个数9的大小;若n≤9,则返回第二步;若n>9,则结束.
开始
n=1
程序框图
输入r
r≥6.8?
是
n=n+1
n>9?
是
否
输出r
否
结束
直到型循环结构
8.(P20BT1)设计一个求解二元一次方程组
其中 的算法,并画出程序框图.
①
②
算法分析:
第一步:判断a1是否等于0.
如果a1≠0,
由②+①×u,得 (b2+b1u)y=c2+c1u; ③
如果a1=0,
执行第三步.
第二步:解③,得
输出y.
第三步:将y值代入②,得
输出x.
开始
程序框图
输入a1,b1,c1,a2,b2,c2
a1≠0?
是
u=-a2/a1
b=b2+b1u
c=c2+c1u
y=c/b
x=(c2-b2y)/a2
否
y=c1/b1
输出x,y
结束
回文数是指从左到右读与从右到左读都是一样的正整数,如121,676,94249,234432等.
9.(P51页B组T3)设计一个算法,判断一个正的n(n>2)位数是不是回文数,用自然语言描述算法步骤.
算法步骤:
第一步:输入一个正整数x和它的位数.
第二步:判断n是不是偶数,如果是偶数,令m=n/2;如果是奇数,令m=(n-1)/2.
第三步:当i从1取到m值时,依次判断x的第i位与第(n+1-i)位上的数字是不是相等,如果都相等,则x是回文数;否则,x不是回文数.
开始
程序框图
输入正整数x和它的位数n
n是偶数?
是
m=n/2
否
m=(n-1)/2
第i位与第(n+1-i)(i=1,2,…,m)位上的数字相等?
是
x是回文数
否
x不是回文数
结束
1.1.1算法的概念
1.1.1 算法的概念
学习目标:
通过分析具体问题过程与步骤,体会算法的思想,了解算法的含义,能用自然语言描述解决具体问题的算法.
学习重点(难点):
通过实例体会算法思想,初步理解算法的含义.
问题1:请你写出解二元一次方程组的详细求解过程.
①
②
第一步:②-①×2得: 5y=3 ③
第二步: 解③得:
第三步: 将 代入①,解得 .
对于一般的二元一次方程组
其中 也可以按照上述步骤求解.
这些步骤就构成了解二元一次方程组的算法,我们可以根据这一算法编制计算机程序,让计算机来解二元一次方程组.
算法的概念与特征:
算法(algorithm)这个词出现于12世纪,指的是用阿拉伯数字进行算术运算的过程.
在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
说明:
(1)事实上算法并没有精确化的定义.
(2)算法虽然没有一个明确的定义,但其特点是鲜明的,不仅要注意算法的程序性、有限性、构造性、精确性的特点,还应该充分理解算法问题的指向性,即算法往往指向解决某一类问题,泛泛地谈算法是没有意义的。
算法学的发展
随着科学技术的日新月异,算法学也得到了前所未有的发展,现在已经发展到了各个领域.有遗传算法,排序算法,加密算法,蚁群算法等,与生物学,计算机科学等有着很广泛的联系,尤其是在现在的航空航天中,更是有着更广泛的应用.
很多复杂的运算都是借助计算机和算法来完成的,在高端科学技术中有着很重要的地位.
例1:
(1)设计一个算法,判断7是否为质数;
(2)设计一个算法,判断35是否为质数。
问题:任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定.
分析:请回顾这个问题的解题过程.
算法分析:
第一步:判断n是否等于2.
若n=2,则n是质数;
若n>2,则执行第二步.
第二步:依次检验2~(n-1)这些整数是不是n的因素,即是不是整除n的数.若有这样的数,则n不是质数;若没有这样的数,则n是质数.
说明:用语言描述一个算法,最便捷的方式就是按解决问题的步骤进行描述.每一步做一件事情.
问题:
设计一个算法,判断整数n(n>2)是否为质数.
第二步:令i=2.
第三步:用i除n,得到余数r
第一步:给定大于2的整数n;
第四步:判断“r=0”是否成立,若是,则n不是质数,结束算法;否则,将i的值增加1,仍用i表示
第五步:判断“i>(n-1)”是否成立,若是,则n是质数,结束算法;否则,返回第三步。
例2:用二分法设计一个求方程x2-2=0的近似根的算法.
算法分析:
设所求近似根与精确解的差的绝对值不超过ε=0.005.
例2.用二分法设计一个求方程x2-2=0是近似根的算法。
算法分析:假设精确度为0.005
第一步:令f(x)=x2-2,因为f (1)<0,f (2)>0,所以设a=1,b=2;
第二步:令 ,判断f (m)是否为0,若是,则m为所求;
若否,则继续判断f (a)·f (m)大于0还是小于0;
a
b
|a-b|
1
2
1
1
1.5
0.5
1.25
1.5
0.25
1.375
1.5
0.125
1.375
1.4375
0.0625
1.40625
1.4375
0.03125
1.40625
1.421875
0.015625
1.4140625
1.421875
0.0078125
1.4140625
1.41796875
0.00390625
点评: (1)上述算法也是求 的近似值的算法.
(2)与一般的解决问题的过程比较,算法有以下特征:
①设计一个具体问题的算法时,与过去熟悉地解数学题的过程有直接的联系,但这个过程必须被分解成若干个明确的步骤,而且这些步骤必须是有效的.
②算法要“面面俱到”,不能省略任何一个细小的步骤,只有这样,才能在人设计出算法后,把具体的执行过程交给计算机完成.
计算机解决任何问题都要依赖于算法.只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”准确地描述出来,计算机才能够解决问题.
例3.试给出一个判断一元二次方程ax2+bx+c=0解的个数的算法.
算法:
第一步:输入a、b、c的值.
第二步:计算? =b2-4ac的值.
第三步:若?>0,则原方程有两个不等的实根;
若?=0,则原方程只有一个实根;
若?<0,则原方程无实根.
第四步:输出结果.
小结:
1、算法:解决问题的过程或步骤;
2、算法的特点:
(1)有限性;
(2)确定性;
(3)可行性;
(4)不唯一性.
作业:
课堂练习:P5 练习1、2
课外作业:P20 习题1.1 A组 1、2
(只需用自然语言写出算法步骤)
练习一:任意给定一个正实数,设计一个算法求以这个数为半径的圆的面积.
算法分析:
第一步:输入任意一个正实数r;
第二步:计算以r为半径的圆的面积S=πr2;
第三步:输出圆的面积.
练习二:任意给定一个大于1的正整数n,设计一个算法求出n的所有因数.
算法分析:
第一步:依次从2~(n-1)为除数去除n,判断余数是否为0,若是,则是n的因数;若不是,则不是n的因数.
第二步:在n的因数中加入1和n;
第三步:输出n的所有因数.
练习三:为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m3的部分,每立方米收费1.5元,并加收0.4元的城市污水处理费,请你写出某户居民每月应交纳的水费y(元)与用水量x(m3)之间的函数关系,然后设计一个求该函数值的算法.
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
求该函数值的算法分析:
第一步:输入每月用水量x;
第二步:判断x是否不超过7.若是,则y=1.2x;若否,则y=1.9x-4.9.
第三步:输出应交纳的水费y.
1.1.2 程序框图
学习目标:(1)在具体问题的解决过程中,掌握基本的程序框图的画法,理解程序框图的三种基本逻辑结构---顺序结构、条件结构、循环结构。
(2)通过模仿、操作、探索,经历通过设计程序框图表达解决问题的算法的过程。
学习重点:通过模仿、操作、探索,经历通过设计程序框图表达求解问题的过程,在具体问题解决过程中,理解程序框图的三种基本逻辑结构.
学习难点:用程序框图清晰表达含有循环结构的算法.
例1:任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定.
算法分析:
第一步:判断n是否等于2.
若n=2,则n是质数;
若n>2,则执行第二步.
第二步:依次检验2~(n-1)这些整数是不是n的因素,即是不是整除n的数.若有这样的数,则n不是质数;若没有这样的数,则n是质数.
从上节课我们知道:算法可以用自然语言来描述.如例1
为了使算法的程序或步骤表达得更为直观,我们更经常地用图形方式来表示它.
开始
输入n
i=2
求n除以i的余数r
i的值增加1仍用i表示
i≥n或r=0?
n不是质数
结束
是
否
是
n是质数
否
r=0?
设n是一个大于2的整数.
一般用i=i+1表示.
i=i+1
说明:i表示从2~(n-1)的所有正整数,用以判断例1步骤2是否终止,i是一个计数变量,有了这个变量,算法才能依次执行.逐步考察从2~(n-1)的所有正整数中是否有n的因数存在.
思考?通过上述算法的两种不同表达方式的比较,你觉得用程序框图来表达算法有哪些特点?
用程序框图表示的算法更加简练,直观,流向清楚.
程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
通常,程序框图由程序框和流程线组成.
一个或几个程序框的组合表示算法中的一个步骤;
流程线是方向箭头,按照算法进行的顺序将程序框连接起来.
1、程序框图
基本的程序框和它们各自表示的功能如下:
图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不”成立时标明“否”或“N”.
判断框
赋值、计算
流程线
连接程序框
连接点
连接程序框图的两部分
开始
输入n
i=2
求n除以i的余数r
i=i+1
i≥n或r=0?
n不是质数
结束
是
否
是
n是质数
否
r=0?
顺序结构
用程序框图来表示算法,有三种不同的基本逻辑结构:
条件结构
循环结构
程序框图的三种基本的逻辑结构
顺序结构
条件结构
循环结构
2、算法的基本逻辑结构:
输入n
i=2
顺序结构
是
n不是质数
n是质数
否
r=0?
条件结构
求n除以i的余数r
i=i+1
i≥n或r=0?
是
否
循环结构
(1)顺序结构-----是由若干个依次执行的处理步骤组成的.这是任何一个算法都离不开的基本结构.
思考?你能说出这三种基本逻辑结构的特点吗?条件结构与循环结构有什么区别和联系?
顺序结构可以用程序
框图表示为
步骤n
步骤n+1
已知三角形三边长分别为a,b,c,则三角形的面积为
其中
这个公式被称为海伦—秦九韶公式.
例3、已知一个三角形的三边边长分别为2,3,4,利用海伦-秦九韶公式设计一个算法,求出它的面积,画出算法的程序框图.
算法分析:
第一步:计算p的值.
第二步:由海伦-秦九韶公式求出三角形的面积S.
第三步:输出S的值.
程序框图:
开始
输出S
结束
画出:已知三角形的三边长a,b,c,求它的面积的程序框图.
开始
输出S
结束
输入a,b,c
(2)条件结构---在一个算法中,经常会遇到一些条件的判断,算法的流向根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.
常见的条件结构可以用程序框图表示为下面两种形式:
满足条件?
是
步骤A
否
步骤B
满足条件?
是
步骤A
否
例4、任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在.画出这个算法的程序框图.
算法分析:
第一步:输入3个正实数a,b,c;
第二步:判断a+b>c,a+c>b,b+c>a是否同时成立,若是,则能组成三角形;若否,则组不成三角形.
程序框图:
开始
输入a,b,c
a+b>c,a+c>b,b+c>a是否
同时成立?
是
存在这样的
三角形
不存在这样的
三角形
否
结束
补例、为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m3的部分,每立方米收费1.5元,并加收0.4元的城市污水处理费,请你写出某户居民每月应交纳的水费y(元)与用水量x(m3)之间的函数关系,然后设计一个求该函数值的算法,并画出程序框图.
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
解:y与x之间的函数关系为:
(当0≤x≤7时)
(当x>7时)
算法分析:
第一步:输入每月用水量x;
第二步:判断x是否不超过7.若是,则y=1.2x;若否,则y=1.9x-4.9.
第三步:输出应交纳的水费y.
开始
输入x
0
y=1.2x
否
y=1.9x-4.9
输出y
结束
程序框图
补例、画程序框图,对于输入的x值,输出相应的y值.
开始
程序框图
x<0?
是
y=0
否
0≤x<1?
是
y=1
否
y=x
输出y
结束
输入x
是
例5.设计一个求任意数的绝对值的算法,并画出程序框图.
算法分析:
第一步:输入数x;
第二步:判断x≥0是否成立?若是,则|x|=x;若否,则|x|=-x.
程序框图:
开始
输入x
x≥0?
输出x
否
输出-x
结束
算法分析:
解决这一问题的算法步骤如下:
开始
程序框图
输入a,b,c
结束
是
是
否
否
输出“方程没
有实数根”
作业:
课本P20页练习,
P21页A组T1;
(画出程序框图)
(3)循环结构---在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一步骤的情况,这就是循环结构.
反复执行的步骤称为循环体.
注意:循环结构不能是永无终止的“死循环”,一定要在某个条件下终止循环,这就需要条件结构来作出判断,因此,循环结构中一定包含条件结构.
说明:(1)一般地,循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,同时它的取值还用于判断循环是否终止,累加变量用于输出结果.累加变量和计数变量一般是同步执行的,累加一次,记数一次.
(2)循环结构分为两种------当型和直到型.
当型循环在每次执行循环体前对循环条件进行判断,当条件满足时执行循环体,不满足则停止;(当条件满足时反复执行循环体)
直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.(反复执行循环体,直到条件满足)
(2)循环结构分为两种------当型和直到型.
直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体,满足则停止.(反复执行循环体,直到条件满足)
循环体
满足条件?
否
是
(2)循环结构分为两种------当型和直到型.
当型循环在每次执行循环体前对循环条件进行判断,当条件满足时执行循环体,不满足则停止;(当条件满足时反复执行循环体)
循环体
满足条件?
否
是
例6、设计一个计算1+2+3+……+100的值的算法,并画出程序框图.
算法分析:
第1步:0+1=1;
第2步:1+2=3;
第3步:3+3=6;
第4步:6+4=10
…………
第100步:4950+100=5050.
第(i-1)步的结果+i=第i步的结果
各步骤有共同的结构:
为了方便有效地表示上述过程,我们引进一个累加变量S来表示每一步的计算结果,从而把第i步表示为 S=S+i
S的初始值为0,i依次取1,2,…,100,
由于i同时记录了循环的次数,所以i称为计数变量.
程序框图:
开始
i=1
S=0
S=S+i
i=i+1
i>100?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤100?
是
S=S+i
i=i+1
否
输出S
结束
当型循环结构
思考?(P15)
程序框图:
开始
i=1
S=0
S=S+i
i=i+1
i>n?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤n?
是
S=S+i
i=i+1
否
输出S
结束
当型循环结构
输入n
输入n
例7、某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.
算法分析:
先写出解决本例的算法步骤:
第一步,输入2005年的年生产总值.
第二步,计算下一年的年生产总值.
第三步,判断所得的结果是否大于300.若是,则输出该年的年份;否则,返回第二步.
由于“第二步”是重复操作的步骤,所以本例可以用循环结构来实现.我们按照“确定循环体”“初始化变量”“设定循环控制条件”的顺序来构造循环结构.
程序框图:
开始
n=2005
a=200
t=0.05a
a=a+t
a>300?
是
结束
直到型循环结构
n=n+1
输出n
否
3、程序框图的画法:
在用自然语言表述一个算法后,可以画出程序框图,用顺序结构、条件结构和循环结构来表示这个算法.这样表示的算法清楚、简练,便于阅读和交流.
若是,则m
为所求;
探究:画出用二分法求方程x2-2=0的近似根(精确度为0.005)的程序框图.
算法分析:
第一步:令f(x)=x2-2.
因为f(1)<0,f(2)>0,
所以设a=1,b=2.
第二步:令
判断f(m)是否为0.
若否,则继续判断f(a) f(m)大于0还是小于0.
第三步:若f(a) f(m)>0,则令a=m;否则,令b=m.
第四步:判断|a-b|<ε是否成立?若是,则a或b为满足条件的近似根;若否,则返回第二步.
(1)算法步骤中的“第一步”“第二步”和“第三步”可以用顺序结构来表示(图1.1-17)
图1.1-17
f(x)=x2-2
输入精确度d
和初始值a,b
b=m
f(a) f(m)<0?
是
a=m
否
图1.1-18
是
第三步
第四步
图1.1-19
否
(4)将各步骤的程序框图连接起来,并画出“开始”与“结束”两个终端框,就得到了表示整个算法的程序框图.
从以上过程可以看出,设计一个算法的程序框图通常要经过以下步骤:
第一步,用自然语言表述算法步骤.
第二步,确定每一个算法步骤所包含的逻辑结构,并用相应的程序框图表示,得到该步骤的程序框图.
第三步,将所有步骤的程序框图用流程线连接起来,并加上终端框,得到表示整个算法的程序框图.
是
是
否
f(a) f(m)>0?
程序框图
开始
f(x)=x2-2
输入误差ε
和初值a,b
a=m
否
b=m
|a-b|<ε或f(m)=0?
输出m
结束
否
是
是
否
f(a) f(m)>0?
程序框图
开始
f(x)=x2-2
输入误差ε
和初值a,b
f(m)=0?
a=m
否
b=m
|a-b|<ε?
1
2
2
输出a和b
结束
输出m
3
1
3
是
课堂小结
本节主要讲述了程序框图的基本知识:包括常用的图形符号、算法的基本逻辑结构.
算法的基本逻辑结构有三种,即顺序结构、条件结构和循环结构.
其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,它们共同构成了算法的基本结构,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达.
作业:
课本P20 A组2、3.
习题练习
是
1.(P20页A组T3)某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元。设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图。
程序框图:
开始
输入x
x>3?
否
结束
输入y
y=5
y=1.2x+1.4
是
2.(P50页A组T3)某市固定电话(市话)的收费标准为:3分钟之内(包括3分钟)收取0.30元;超过3分钟,每分钟(不足一分钟,按一分钟计算)按0.10元收费。设计一个算法,根据通话时间计算话费。
程序框图:
开始
输入t
0
结束
输出y
y=0.3
y=0.1t
3.P50页A组T1(1)画程序框图,对于输入的x值,输出相应的y值:
开始
程序框图
x<0?
是
y=0
否
0≤x<1?
是
y=1
否
y=x
输出y
结束
输入x
4.P50页A组T1(2)画程序框图,对于输入的x值,输出相应的y值:
开始
程序框图
x<0?
是
y=(x+2)2
否
x=0?
是
y=4
否
输出y
结束
输入x
y=(x-2)2
开始
i=1
S=0
S=S+i2
i=i+1
i>100?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤100?
是
S=S+i2
i=i+1
否
输出S
结束
当型循环结构
5.P20页A组T2.
开始
i=1
S=0
S=S+
i=i+1
i>n?
是
输出S
结束
否
直到型循环结构
开始
i=1
S=0
i≤n?
是
S=S+
i=i+1
否
输出S
结束
当型循环结构
6.P50页A组T4.
输入n
输入n
7.(P20BT2).某高中男子体育小组的50m跑成绩(单位:s)为: 6.4, 6.5, 7.0, 6.8, 7.1, 7.3, 6.9, 7.4, 7.5.
设计一个算法,从这些成绩中搜出小于6.8s的成绩.
算法分析:
第一步:把计数变量n的初值设为1.
第二步:输入一个成绩r,判断r与6.8的大小.若r≥6.8,则执行下一步;若r<6.8,则输出r,并执行下一步.
第三步:使计数变量n的值增加1.
第四步:判断计数变量n与成绩个数9的大小;若n≤9,则返回第二步;若n>9,则结束.
开始
n=1
程序框图
输入r
r≥6.8?
是
n=n+1
n>9?
是
否
输出r
否
结束
直到型循环结构
8.(P20BT1)设计一个求解二元一次方程组
其中 的算法,并画出程序框图.
①
②
算法分析:
第一步:判断a1是否等于0.
如果a1≠0,
由②+①×u,得 (b2+b1u)y=c2+c1u; ③
如果a1=0,
执行第三步.
第二步:解③,得
输出y.
第三步:将y值代入②,得
输出x.
开始
程序框图
输入a1,b1,c1,a2,b2,c2
a1≠0?
是
u=-a2/a1
b=b2+b1u
c=c2+c1u
y=c/b
x=(c2-b2y)/a2
否
y=c1/b1
输出x,y
结束
回文数是指从左到右读与从右到左读都是一样的正整数,如121,676,94249,234432等.
9.(P51页B组T3)设计一个算法,判断一个正的n(n>2)位数是不是回文数,用自然语言描述算法步骤.
算法步骤:
第一步:输入一个正整数x和它的位数.
第二步:判断n是不是偶数,如果是偶数,令m=n/2;如果是奇数,令m=(n-1)/2.
第三步:当i从1取到m值时,依次判断x的第i位与第(n+1-i)位上的数字是不是相等,如果都相等,则x是回文数;否则,x不是回文数.
开始
程序框图
输入正整数x和它的位数n
n是偶数?
是
m=n/2
否
m=(n-1)/2
第i位与第(n+1-i)(i=1,2,…,m)位上的数字相等?
是
x是回文数
否
x不是回文数
结束
