高中数学人教A版必修三课件-1.1.1 算法的概念(31张PPT)
文档属性
| 名称 | 高中数学人教A版必修三课件-1.1.1 算法的概念(31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览











文档简介
现代社会,计算机几乎已触及到人们生活的方方面面,为人们的生活提供了很多便利,那计算机是如何工作的呢?如何才能让它发挥更大的作用呢?事实上,计算机的应用离不开程序设计,而程序设计就是算法设计,所以要从算法说起.一起来认识算法吧!
1.1 算法与程序框图
第一章
1.1.1 算法的概念
在数学的学习中,我们经常会对一类问题的解法进行归纳总结,得出解决这一类问题的一般步骤或方法,如解一元二次不等式的一般步骤是:(1)化一元二次不等式为一般形式(ax2+bx+c≥0或ax2+bx+c≤0,其中a>0);(2)求出该一元二次不等式对应的一元二次方程的实数根;(3)写出不等式的解集.这实际上就是算法的思想。
随着计算机科学和信息技术的飞速发展,算法的思想已渗透到社会的方方面面,这一节我们就来学习算法.
●知识衔接
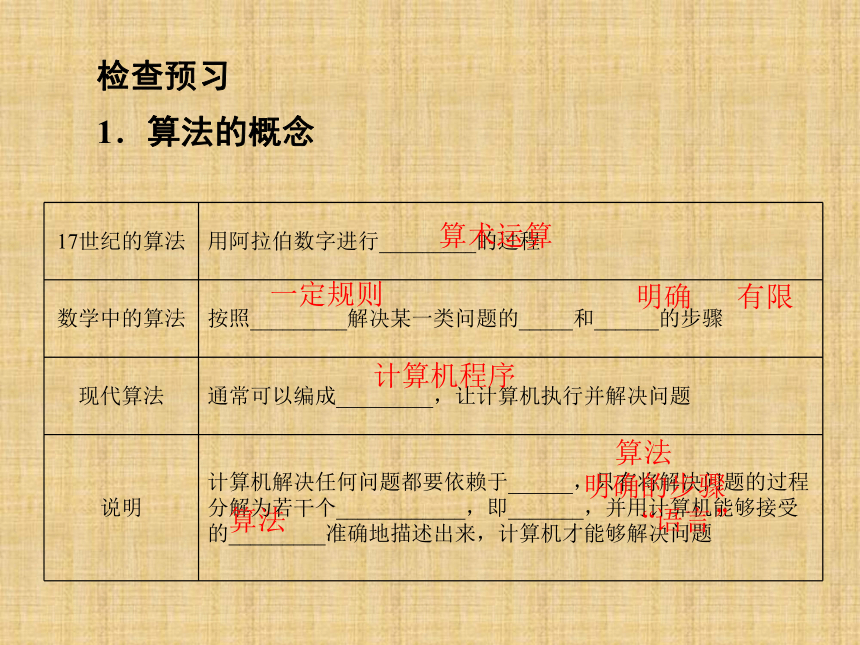
检查预习
1.算法的概念
17世纪的算法
用阿拉伯数字进行_________的过程
数学中的算法
按照_________解决某一类问题的_____和______的步骤
现代算法
通常可以编成_________,让计算机执行并解决问题
说明
计算机解决任何问题都要依赖于______,只有将解决问题的过程分解为若干个____________,即_______,并用计算机能够接受的_________准确地描述出来,计算机才能够解决问题
算术运算
一定规则
明确
有限
计算机程序
算法
明确的步骤
算法
“语言”
[破疑点]算法与一般意义上具体问题的解法既有联系又有区别,它们之间是一般与特殊、抽象与具体的关系.算法的获得要借助于一般意义上具体问题的求解方法,而任何一个具体问题都可以利用这类问题的一般算法来解决.在解决某些问题时,需要设计出一系列可操作或可计算的步骤,这些步骤称为解决这些问题的算法.这种用步骤呈现解决问题过程的思想方法称为算法的思想.
2.算法的特征
算法是做一件事情的方法和步骤.在生活中做一件事情的方法和步骤有多种,我们设计的算法应本着简捷方便的原则.要正确地设计一个算法就需要了解算法的特征:
特征
说明
有限性
一个算法当运行完有限个步骤后必须结束,而不能是无限地运行
确定性
算法的每一步计算,都必须有确定的结果,不能模棱两可,即算法的每一步只有唯一的执行路径,对于相同的输入只能得到相同的输出结果
特征
说明
可行性
算法中的每一步骤必须能用实现算法的工具精确表达,并能在有限步内完成
有序性
算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后续步骤,只有执行完前一步才能执行后一步
普遍性
算法一般要适用于输入值集合中不同形式的输入值,而不是局限于某些特殊的值,即算法具有一般性,一个算法总是针对某类问题设计的,所以对于求解这类问题中的任意一个问题都应该是有效的
不唯一性
解决一个或一类问题,可以有不同的方法和步骤,也就是说,解决这个或这类问题的算法不一定是唯一的
3.算法的设计
(1)算法设计的目的
设计算法的目的实际上是寻求__________的算法,它可以通过计算机来完成.设计算法的关键是把过程分解成若干个__________,然后用计算机能够接受的“语言”准确地描述出来,从而达到计算机执行的目的.
(2)算法设计的要求
①写出的算法必须能解决__________;
②要使算法尽量____、步骤尽量___;
③要保证算法____,且计算机能够_____.
一类问题
是确的步骤
一类问题
简单
少
正确
执行
(3)算法的描述
①展现形式:目前可使用文字语言表示.
②展现方式:算法常用下列方式来表示:
第一步,……
第二步,……
第三步,……
……
[答案] D
●跟踪测试
[解析] A、B两选项给出了解决问题的方法和步骤,是算法.C项,利用公式计算也属于算法.D项,只提出问题没有给出解决的方法,不是算法.
[警误区] 算法特征中的有限性不等同于步骤的有限步,在算法结构中会出现步骤的重复使用,也就是说算法执行的步数大于或等于步骤中的步数,很可能步骤中的步数较少而要执行的步骤很多,但不可以无限.
2.有蓝和黑两个墨水瓶,但现在却错把蓝墨水装在了黑墨水瓶中,黑墨水错装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题.
[分析] 由于两个墨水瓶中的墨水不能直接交换,故可以考虑通过引入第三个空墨水瓶的办法进行交换.
[答案] 解:算法步骤如下:
第一步,取一只空的墨水瓶,设其为白色.
第二步,将黑墨水瓶中的蓝墨水装入白瓶中.
第三步,将蓝墨水瓶中的黑墨水装入黑瓶中.
第四步,将白瓶中的蓝墨水装入蓝瓶中.
第五步,交换结束.
(1)下列关于算法的描述正确的是( )
A.算法与求解一个问题的方法相同
B.算法只能解决一个问题,不能重复使用
C.算法过程要一步一步执行,每步执行的操作必须确切
D.有的算法执行完后,可能无结果
算法含义的正确理解
●互动探究
(2)下列描述不能看作算法的是( )
A.做米饭需要刷锅,淘米,添水,加热这些步骤
B.洗衣机的使用说明书
C.解不等式2x2+x-1>0
D.求过M(1,2)与N(-3,-5)两点的直线方程可以先求MN的斜率,再利用点斜式方程求得.
[解析] (1)算法与求解一个问题的方法既有区别又有联系,故A项不对;算法能重复使用,故B项不对;每个算法执行后必须有结果,故D项不对;由算法的有序性和确定性可知C项正确.
(2)A、B、D都描述了解决问题的过程,可以看作算法,而C只描述了一个事实,没说明怎么解决问题,不是算法.
[答案] (1)C (2)C
[探究] 1.算法有何特点?
2.如何判断一个语句是否可以看作算法?
[规律总结] (1)算法实际上是一种程序性方法,它通常解决某一个或一类问题,在用算法解决问题时,显然体现了特殊与一般的数学思想.
(2)算法的特点有:①有限性,②确定性,③顺序性与正确性,④不唯一性,⑤普遍性.解答有关算法的概念判断题应根据算法的这五大特点.
课堂练习
(1)下列关于算法的说法正确的是( )
A.某个问题的解题过程就是算法
B.一个算法可以有无穷多个步骤
C.解决某一问题的算法可以有多个
D.算法执行完后可以有多个不同的结果
[解析] 算法与求解一个问题的方法过程是有区别的,故A不对;每一个算法的步骤是有限的,且执行后结果是唯一确定的,故B、D不对;解决某一问题的算法可以不同,故C正确.
[答案] (2)①④
(2)①是学习数学的一个有效的步骤,故它是算法;
②不是李华吃饭的步骤,只是说明他吃了多少东西,故它不是算法;
③执行结果不确定,故它也不是算法;
④是求菱形面积的步骤,故它是算法.
[规律总结] 判断算法的三个关注点
(1)明确算法的含义.
(2)明确算法的特点.
(3)明确算法与解法的区别.
写出求1+2+3+4+5+6的一个算法.
数值性问题的算法
[解析] 算法1:
第一步,计算1+2得到3;
第二步,将第一步中的运算结果3与3相加得到6;
第三步,将第二步中的运算结果6与4相加得到10;
第四步,将第三步中的运算结果10与5相加得到15;
第五步,将第四步中的运算结果15与6相加得到21;
第六步,输出运算结果.
[规律总结] (1)算法1是切合“算法”的含义.算法2是运用已知的结果作为公式进行计算.算法3据已知发现规律写出步骤.
(2)算法设计的步骤
设计一个具体的算法,通常按以下步骤:
非数值性问题的算法
试设计一个算法,求表面积为16π的球的体积.
算法的应用
●探索延拓
(1)一个算法的步骤如下:
第一步,输入x的值.
第二步,计算y=x2.
第三步,计算z=2y-log2y.
第四步,输出z的值.
若输入x的值为-2,则输出z的值为( )
A.2 B.4
C.12 D.14
[解析] (1)第一步,输入x的值为-2,第二步,计算得y=(-2)2=4;第三步,计算得z=24-log24=16-2=14.
[答案] (1)D
课堂 检 测
1.下面的结论正确的是( )
A.算法步骤是可逆的
B.一个算法可以无止境地运算下去
C.完成一件事情的算法有且只有一种
D.设计算法要本着简单方便的原则
[答案] D
[解析] A错,不一定可逆;B错,算法必须在有限步之内完成;C错,可以有多种;D正确.
2.下列可以看成算法的是( )
A.高中学习的基本步骤是预习、听课、做作业
B.今天餐厅的饭真好吃
C.这道数学题难做
D.方程2x2-x+1=0无实数根
[答案] A
3.判断5是否为质数的算法步骤如下:
第一步:用2除5,得余数为1.因为余数不为0,所以2不能整除5;
第二步:________;
第三步:用4除5,得余数为1.因为余数不为0,所以4不能整除5.因此,5是质数.
[答案] 用3除5,得余数为2.因为余数不为0,所以3不能整除5.
完成教科书第5页练习第1、2题
布置作业
1.1 算法与程序框图
第一章
1.1.1 算法的概念
在数学的学习中,我们经常会对一类问题的解法进行归纳总结,得出解决这一类问题的一般步骤或方法,如解一元二次不等式的一般步骤是:(1)化一元二次不等式为一般形式(ax2+bx+c≥0或ax2+bx+c≤0,其中a>0);(2)求出该一元二次不等式对应的一元二次方程的实数根;(3)写出不等式的解集.这实际上就是算法的思想。
随着计算机科学和信息技术的飞速发展,算法的思想已渗透到社会的方方面面,这一节我们就来学习算法.
●知识衔接
检查预习
1.算法的概念
17世纪的算法
用阿拉伯数字进行_________的过程
数学中的算法
按照_________解决某一类问题的_____和______的步骤
现代算法
通常可以编成_________,让计算机执行并解决问题
说明
计算机解决任何问题都要依赖于______,只有将解决问题的过程分解为若干个____________,即_______,并用计算机能够接受的_________准确地描述出来,计算机才能够解决问题
算术运算
一定规则
明确
有限
计算机程序
算法
明确的步骤
算法
“语言”
[破疑点]算法与一般意义上具体问题的解法既有联系又有区别,它们之间是一般与特殊、抽象与具体的关系.算法的获得要借助于一般意义上具体问题的求解方法,而任何一个具体问题都可以利用这类问题的一般算法来解决.在解决某些问题时,需要设计出一系列可操作或可计算的步骤,这些步骤称为解决这些问题的算法.这种用步骤呈现解决问题过程的思想方法称为算法的思想.
2.算法的特征
算法是做一件事情的方法和步骤.在生活中做一件事情的方法和步骤有多种,我们设计的算法应本着简捷方便的原则.要正确地设计一个算法就需要了解算法的特征:
特征
说明
有限性
一个算法当运行完有限个步骤后必须结束,而不能是无限地运行
确定性
算法的每一步计算,都必须有确定的结果,不能模棱两可,即算法的每一步只有唯一的执行路径,对于相同的输入只能得到相同的输出结果
特征
说明
可行性
算法中的每一步骤必须能用实现算法的工具精确表达,并能在有限步内完成
有序性
算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后续步骤,只有执行完前一步才能执行后一步
普遍性
算法一般要适用于输入值集合中不同形式的输入值,而不是局限于某些特殊的值,即算法具有一般性,一个算法总是针对某类问题设计的,所以对于求解这类问题中的任意一个问题都应该是有效的
不唯一性
解决一个或一类问题,可以有不同的方法和步骤,也就是说,解决这个或这类问题的算法不一定是唯一的
3.算法的设计
(1)算法设计的目的
设计算法的目的实际上是寻求__________的算法,它可以通过计算机来完成.设计算法的关键是把过程分解成若干个__________,然后用计算机能够接受的“语言”准确地描述出来,从而达到计算机执行的目的.
(2)算法设计的要求
①写出的算法必须能解决__________;
②要使算法尽量____、步骤尽量___;
③要保证算法____,且计算机能够_____.
一类问题
是确的步骤
一类问题
简单
少
正确
执行
(3)算法的描述
①展现形式:目前可使用文字语言表示.
②展现方式:算法常用下列方式来表示:
第一步,……
第二步,……
第三步,……
……
[答案] D
●跟踪测试
[解析] A、B两选项给出了解决问题的方法和步骤,是算法.C项,利用公式计算也属于算法.D项,只提出问题没有给出解决的方法,不是算法.
[警误区] 算法特征中的有限性不等同于步骤的有限步,在算法结构中会出现步骤的重复使用,也就是说算法执行的步数大于或等于步骤中的步数,很可能步骤中的步数较少而要执行的步骤很多,但不可以无限.
2.有蓝和黑两个墨水瓶,但现在却错把蓝墨水装在了黑墨水瓶中,黑墨水错装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题.
[分析] 由于两个墨水瓶中的墨水不能直接交换,故可以考虑通过引入第三个空墨水瓶的办法进行交换.
[答案] 解:算法步骤如下:
第一步,取一只空的墨水瓶,设其为白色.
第二步,将黑墨水瓶中的蓝墨水装入白瓶中.
第三步,将蓝墨水瓶中的黑墨水装入黑瓶中.
第四步,将白瓶中的蓝墨水装入蓝瓶中.
第五步,交换结束.
(1)下列关于算法的描述正确的是( )
A.算法与求解一个问题的方法相同
B.算法只能解决一个问题,不能重复使用
C.算法过程要一步一步执行,每步执行的操作必须确切
D.有的算法执行完后,可能无结果
算法含义的正确理解
●互动探究
(2)下列描述不能看作算法的是( )
A.做米饭需要刷锅,淘米,添水,加热这些步骤
B.洗衣机的使用说明书
C.解不等式2x2+x-1>0
D.求过M(1,2)与N(-3,-5)两点的直线方程可以先求MN的斜率,再利用点斜式方程求得.
[解析] (1)算法与求解一个问题的方法既有区别又有联系,故A项不对;算法能重复使用,故B项不对;每个算法执行后必须有结果,故D项不对;由算法的有序性和确定性可知C项正确.
(2)A、B、D都描述了解决问题的过程,可以看作算法,而C只描述了一个事实,没说明怎么解决问题,不是算法.
[答案] (1)C (2)C
[探究] 1.算法有何特点?
2.如何判断一个语句是否可以看作算法?
[规律总结] (1)算法实际上是一种程序性方法,它通常解决某一个或一类问题,在用算法解决问题时,显然体现了特殊与一般的数学思想.
(2)算法的特点有:①有限性,②确定性,③顺序性与正确性,④不唯一性,⑤普遍性.解答有关算法的概念判断题应根据算法的这五大特点.
课堂练习
(1)下列关于算法的说法正确的是( )
A.某个问题的解题过程就是算法
B.一个算法可以有无穷多个步骤
C.解决某一问题的算法可以有多个
D.算法执行完后可以有多个不同的结果
[解析] 算法与求解一个问题的方法过程是有区别的,故A不对;每一个算法的步骤是有限的,且执行后结果是唯一确定的,故B、D不对;解决某一问题的算法可以不同,故C正确.
[答案] (2)①④
(2)①是学习数学的一个有效的步骤,故它是算法;
②不是李华吃饭的步骤,只是说明他吃了多少东西,故它不是算法;
③执行结果不确定,故它也不是算法;
④是求菱形面积的步骤,故它是算法.
[规律总结] 判断算法的三个关注点
(1)明确算法的含义.
(2)明确算法的特点.
(3)明确算法与解法的区别.
写出求1+2+3+4+5+6的一个算法.
数值性问题的算法
[解析] 算法1:
第一步,计算1+2得到3;
第二步,将第一步中的运算结果3与3相加得到6;
第三步,将第二步中的运算结果6与4相加得到10;
第四步,将第三步中的运算结果10与5相加得到15;
第五步,将第四步中的运算结果15与6相加得到21;
第六步,输出运算结果.
[规律总结] (1)算法1是切合“算法”的含义.算法2是运用已知的结果作为公式进行计算.算法3据已知发现规律写出步骤.
(2)算法设计的步骤
设计一个具体的算法,通常按以下步骤:
非数值性问题的算法
试设计一个算法,求表面积为16π的球的体积.
算法的应用
●探索延拓
(1)一个算法的步骤如下:
第一步,输入x的值.
第二步,计算y=x2.
第三步,计算z=2y-log2y.
第四步,输出z的值.
若输入x的值为-2,则输出z的值为( )
A.2 B.4
C.12 D.14
[解析] (1)第一步,输入x的值为-2,第二步,计算得y=(-2)2=4;第三步,计算得z=24-log24=16-2=14.
[答案] (1)D
课堂 检 测
1.下面的结论正确的是( )
A.算法步骤是可逆的
B.一个算法可以无止境地运算下去
C.完成一件事情的算法有且只有一种
D.设计算法要本着简单方便的原则
[答案] D
[解析] A错,不一定可逆;B错,算法必须在有限步之内完成;C错,可以有多种;D正确.
2.下列可以看成算法的是( )
A.高中学习的基本步骤是预习、听课、做作业
B.今天餐厅的饭真好吃
C.这道数学题难做
D.方程2x2-x+1=0无实数根
[答案] A
3.判断5是否为质数的算法步骤如下:
第一步:用2除5,得余数为1.因为余数不为0,所以2不能整除5;
第二步:________;
第三步:用4除5,得余数为1.因为余数不为0,所以4不能整除5.因此,5是质数.
[答案] 用3除5,得余数为2.因为余数不为0,所以3不能整除5.
完成教科书第5页练习第1、2题
布置作业
