必修2 第八章 机械能守恒定律 第1节 功的计算 同步练习
文档属性
| 名称 | 必修2 第八章 机械能守恒定律 第1节 功的计算 同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 247.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-09 15:00:19 | ||
图片预览



文档简介
机械能守恒定律同步练习
功的计算同步练习
(答题时间:30分钟)
1. 质量为m=20 kg的物体,在大小恒定的水平外力F的作用下,沿水平面做直线运动。0~2 s内F与运动方向相反,2~4 s内F与运动方向相同,物体的v-t图象如图所示,g取10 m/s2,则( )
A. 拉力F的大小为100 N
B. 物体在4 s时拉力的瞬时功率为120 W
C. 4 s内拉力所做的功为480 J
D. 4 s内物体克服摩擦力做的功为320 J
2. 如图所示,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止。在前进的水平位移为l的过程中,斜面体对P做功为( )
A. Fl B. mgsinθ·l C. mgcosθ·l D. mgtanθ·l
3. 一滑块在水平地面上沿直线滑行,t=0时其速度为1 m/s。从此刻开始在滑块运动方向上再施加一水平作用力F,力F和滑块的速度v随时间的变化规律分别如图(甲)和(乙)所示。设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3,则以下关系式正确的是 ( )
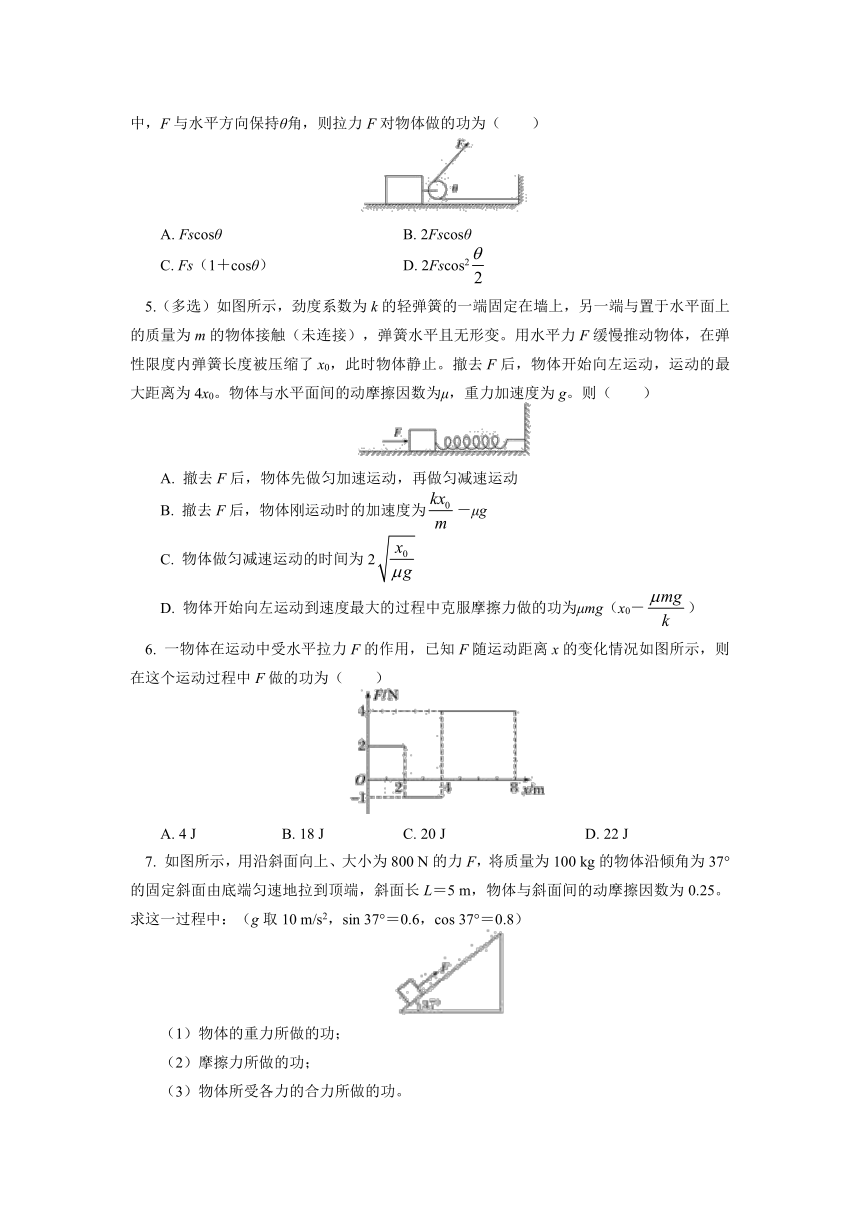
A. W1=W2=W3 B. W1C. W14.(多选)如图所示,一恒力F通过一动滑轮拉物体沿光滑水平面前进了s,在运动过程中,F与水平方向保持θ角,则拉力F对物体做的功为( )
A. Fscosθ B. 2Fscosθ
C. Fs(1+cosθ) D. 2Fscos2
5.(多选)如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上的质量为m的物体接触(未连接),弹簧水平且无形变。用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止。撤去F后,物体开始向左运动,运动的最大距离为4x0。物体与水平面间的动摩擦因数为μ,重力加速度为g。则( )
A. 撤去F后,物体先做匀加速运动,再做匀减速运动
B. 撤去F后,物体刚运动时的加速度为-μg
C. 物体做匀减速运动的时间为2
D. 物体开始向左运动到速度最大的过程中克服摩擦力做的功为μmg(x0-)
6. 一物体在运动中受水平拉力F的作用,已知F随运动距离x的变化情况如图所示,则在这个运动过程中F做的功为( )
A. 4 J B. 18 J C. 20 J D. 22 J
7. 如图所示,用沿斜面向上、大小为800 N的力F,将质量为100 kg的物体沿倾角为37°的固定斜面由底端匀速地拉到顶端,斜面长L=5 m,物体与斜面间的动摩擦因数为0.25。求这一过程中:(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
(1)物体的重力所做的功;
(2)摩擦力所做的功;
(3)物体所受各力的合力所做的功。
功的计算同步练习参考答案
1.【答案】B
【解析】由图象可得:0~2 s内物体做匀减速直线运动,加速度大小为:a1== m/s2=5 m/s2,匀减速过程有F+Ff=ma1。匀加速过程加速度大小为a2==m/s2=1 m/s2,有F-Ff=ma2,解得Ff=40 N,F=60 N,故A错误。物体在4 s时拉力的瞬时功率为P=Fv=60×2 W=120 W,故B正确。4 s内物体通过的位移为x=(×2×10-×2×2)m=8 m,拉力做功为W=-Fx=-480 J,故C错误。4 s内物体通过的路程为s=(×2×10+×2×2) m=12 m,摩擦力做功为Wf=-Ffs=-40×12 J=-480 J,故D错误。
2.【答案】D
【解析】斜面对P的作用力垂直于斜面,其竖直分量为mg,所以水平分量为mgtanθ,做功为水平分量的力乘以水平位移。
3.【答案】B
【解析】解析:由v-t图像可知,物体在第1秒内的位移为x1=0.5m、第2秒内的位移为x2=0.5m、第3秒内的位移为x3=1m;故第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1=F1x1=0.5J、W2=F2x2=1.5J、W3=F3x3=2J。故有W14.【答案】CD
【解析】对F的端点分析,F的作用力沿F的方向移动了,由题意可知,当物体向右移动s时,力的作用点沿力方向移动s的同时也会随滑轮向右移动s,则力的作用点的合位移如图所示,则s合=2scos,则F对物体做功W=Fs合cos=2Fscos2由数学知识可知:2Fscos2=Fs(1+cosθ)。
5.【答案】BD
【解析】撤去F后,在物体离开弹簧的过程中,弹簧弹力是变力,物体先做变加速运动,离开弹簧之后做匀减速运动,故A错;刚开始时,由kx0-μmg=ma可知B正确;离开弹簧之后做匀减速运动,减速时间满足3x0=a1t2,a1=μg则t=,C错;速度最大时合力为零,此时弹簧弹力F=μmg=kx,x=,所以物体开始向左运动到速度最大的过程中克服摩擦力做的功为Wf=μmg(x0-x)=μmg(x0-),D正确。
6.【答案】B
【解析】方法一 由图可知F在整个过程中做功分为三个小过程,分别做功为
W1=2×2 J=4 J,W2=-1×2 J=-2 J
W3=4×4 J=16 J,
所以W=W1+W2+W3=4 J+(-2)J+16 J=18 J。
方法二 F-x图象中图线与x轴所围成的面积表示做功的多少,x轴上方为正功,下方为负功,总功取三部分的代数和,即(2×2-2×1+4×4)J=18 J,B正确。
7.【答案】(1)-3 000 J (2)-1 000 J (3)0
【解析】物体受力情况如图所示
(1)WG=-mgLsinθ=-3 000 J
(2)Ff=μFN=μmgcosθ
Wf=-FfL=-μmgcosθ·L
=-1 000 J
(3)解法一:WF=FL=4 000 J
W=WF+WG+Wf=0
解法二:物体做匀速运动,F合=0
故W=0。
功率及机车启动问题同步练习
(答题时间:30分钟)
1. 水平面上一质量为m的物体,在水平力F作用下开始加速运动,力F的功率P保持恒定,运动过程所受的阻力Ff大小不变,物体速度最终达到稳定值vm,F作用过程物体的速度v的倒数与加速度a的关系图象如图所示,仅在已知功率P的情况下,根据图象所给的信息( )
A. 可求出m,Ff和vm
B. 不能求出m
C. 不能求出Ff
D. 可求出加速运动时间
2. 起重机将质量为m的货物由静止开始以加速度a匀加速提升,在t时间内上升h高度,设在t时间内起重机对货物的拉力做的功为W、平均功率为,则( )
A. W=mah
B. W=mgh
C. =
D. =
3. 一辆质量为m的轿车,在平直公路上运行,启动阶段轿车牵引力保持不变,而后以额定功率继续行驶,经过一定时间,其速度由零增大到最大值vm,若所受阻力恒为Ff。则关于轿车的速度v、加速度a、牵引力F、功率P的图象正确的是( )
A. B.
C. D.
4. 如图所示为某汽车在平直公路上启动时发动机功率P随时间t变化的图象,P0为发动机的额定功率。已知在t2时刻汽车的速度已经达到最大vm,汽车所受阻力不变。由此可得( )
A. 在t3时刻,汽车速度一定等于vm
B. 在t1~t2时间内,汽车一定做匀速运动
C. 在t2~t3时间内,汽车一定做匀速运动
D. 在发动机功率达到额定功率前,汽车一定做匀加速运动
5. 质量为m=5.0×106kg的列车以恒定不变的功率由静止沿平直轨道加速行驶,当速度增大到v1=2 m/s时,加速度a1=0.9 m/s2,当速度增大到v2=10 m/s时,加速度a2=0.1 m/s2,如果列车所受阻力大小不变,求:
(1)列车所受阻力是多少?
(2)在该功率下列车的最大速度是多少?
6. 质量为2 000 kg、额定功率为80 kW的汽车,在平直公路上行驶中的最大速度为20 m/s。若汽车从静止开始做匀加速直线运动,加速度大小为2 m/s2,运动中的阻力不变。求:
(1)汽车所受阻力的大小;
(2)3 s末汽车的瞬时功率;
(3)汽车做匀加速运动的时间;
(4)汽车在匀加速运动中牵引力所做的功;
功率及机车启动问题同步练习参考答案
1.【答案】A
【解析】当加速度为零时,物体做匀速运动,此时的牵引力等于阻力,速度为最大值;由功率的计算公式可得P=Fv,而F-Ff=ma,联立可得=a+,由图象可得斜率为,因此可求出m、Ff和vm,故A正确;物体做变加速运动,加速运动的时间不可求,故D错误。
2.【答案】D
【解析】对货物进行受力分析,货物受重力和起重机对货物的拉力F,根据牛顿第二定律得:F-mg=ma,解得:F=m(a+g),上升h高度,起重机对货物拉力做功W=Fh=m(a+g)h,故A、B错误;由于货物做匀加速运动,平均速度等于过程中的中间时刻速度,所以在t时间内的平均速度为=at,起重机对货物拉力做功平均功率为=F=ma(a+g)t,故C错误,D正确。
3.【答案】ACD
【解析】由于启动阶段轿车受到的牵引力不变,加速度不变,所以轿车在开始阶段做匀加速运动,当实际功率达到额定功率时,功率不增加了,再增加速度,就须减小牵引力,当牵引力减小到等于阻力时,加速度等于零,速度达到最大值vm==,所以A、C、D正确,B错误。
4.【答案】AC
【解析】已知在t2时刻汽车的速度已经达到最大vm,此后汽车做匀速直线运动,速度不变,所以在t3时刻,汽车速度一定等于vm,故A正确;0~t1时间内汽车的功率均匀增加,汽车所受阻力不变,牵引力不变,汽车做匀加速直线运动;汽车的功率在t1时刻达到额定功率,根据P=Fv,速度继续增大,牵引力减小,加速度减小,则在t1~t2时间内汽车做加速度减小的加速运动,故B错误;在t2~t3时间内,汽车已达到最大速度,且功率保持不变,汽车一定做匀速直线运动,故C正确;由此分析知,在发动机功率达到额定功率前,汽车先做匀加速运动,后做加速度减小的变加速运动,故D错误。
5.【答案】(1)5.0×105N (2)20 m/s
【解析】(1)设列车恒定不变的功率为P,大小不变的阻力为Ff,当列车速度增大到v1=2 m/s时,P=F1v1①
由牛顿第二定律可得:F1-Ff=ma1②
当列车速度增大到v2=10 m/s时,P=F2v2③
由牛顿第二定律可得:F2-Ff=ma2④
将①、③分别代入②、④联立方程可解得:
P=1.0×107W,Ff=5.0×105N
(2)该功率下列车以最大速度行驶时,牵引力等于阻力,有P=Fvm=Ffvm
解得vm==20 m/s。
6.【答案】(1)4 000 N (2)4.8×104W (3)5 s (4)2×105J
【解析】(1)以最大速度行驶时,根据P=Fv,得F=4 000 N。而此时牵引力和阻力大小相等。
(2)3 s时的速度v=at=6m/s,而牵引力由F-Ff=ma得F=8 000 N,故此时的功率为P=Fv=4.8×104W。
(3)设匀加速运动的时间为t,则t时刻的速度为v=at,这时汽车的功率为额定功率。由P=Fv,将F=8 000 N和v=at代入得t=5 s。
(4)匀加速运动阶段牵引力为恒力,牵引力所做的功W=Fl=Fat2=8000××2×52J=2×105J
功的计算同步练习
(答题时间:30分钟)
1. 质量为m=20 kg的物体,在大小恒定的水平外力F的作用下,沿水平面做直线运动。0~2 s内F与运动方向相反,2~4 s内F与运动方向相同,物体的v-t图象如图所示,g取10 m/s2,则( )
A. 拉力F的大小为100 N
B. 物体在4 s时拉力的瞬时功率为120 W
C. 4 s内拉力所做的功为480 J
D. 4 s内物体克服摩擦力做的功为320 J
2. 如图所示,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止。在前进的水平位移为l的过程中,斜面体对P做功为( )
A. Fl B. mgsinθ·l C. mgcosθ·l D. mgtanθ·l
3. 一滑块在水平地面上沿直线滑行,t=0时其速度为1 m/s。从此刻开始在滑块运动方向上再施加一水平作用力F,力F和滑块的速度v随时间的变化规律分别如图(甲)和(乙)所示。设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3,则以下关系式正确的是 ( )
A. W1=W2=W3 B. W1
A. Fscosθ B. 2Fscosθ
C. Fs(1+cosθ) D. 2Fscos2
5.(多选)如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上的质量为m的物体接触(未连接),弹簧水平且无形变。用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止。撤去F后,物体开始向左运动,运动的最大距离为4x0。物体与水平面间的动摩擦因数为μ,重力加速度为g。则( )
A. 撤去F后,物体先做匀加速运动,再做匀减速运动
B. 撤去F后,物体刚运动时的加速度为-μg
C. 物体做匀减速运动的时间为2
D. 物体开始向左运动到速度最大的过程中克服摩擦力做的功为μmg(x0-)
6. 一物体在运动中受水平拉力F的作用,已知F随运动距离x的变化情况如图所示,则在这个运动过程中F做的功为( )
A. 4 J B. 18 J C. 20 J D. 22 J
7. 如图所示,用沿斜面向上、大小为800 N的力F,将质量为100 kg的物体沿倾角为37°的固定斜面由底端匀速地拉到顶端,斜面长L=5 m,物体与斜面间的动摩擦因数为0.25。求这一过程中:(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
(1)物体的重力所做的功;
(2)摩擦力所做的功;
(3)物体所受各力的合力所做的功。
功的计算同步练习参考答案
1.【答案】B
【解析】由图象可得:0~2 s内物体做匀减速直线运动,加速度大小为:a1== m/s2=5 m/s2,匀减速过程有F+Ff=ma1。匀加速过程加速度大小为a2==m/s2=1 m/s2,有F-Ff=ma2,解得Ff=40 N,F=60 N,故A错误。物体在4 s时拉力的瞬时功率为P=Fv=60×2 W=120 W,故B正确。4 s内物体通过的位移为x=(×2×10-×2×2)m=8 m,拉力做功为W=-Fx=-480 J,故C错误。4 s内物体通过的路程为s=(×2×10+×2×2) m=12 m,摩擦力做功为Wf=-Ffs=-40×12 J=-480 J,故D错误。
2.【答案】D
【解析】斜面对P的作用力垂直于斜面,其竖直分量为mg,所以水平分量为mgtanθ,做功为水平分量的力乘以水平位移。
3.【答案】B
【解析】解析:由v-t图像可知,物体在第1秒内的位移为x1=0.5m、第2秒内的位移为x2=0.5m、第3秒内的位移为x3=1m;故第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1=F1x1=0.5J、W2=F2x2=1.5J、W3=F3x3=2J。故有W1
【解析】对F的端点分析,F的作用力沿F的方向移动了,由题意可知,当物体向右移动s时,力的作用点沿力方向移动s的同时也会随滑轮向右移动s,则力的作用点的合位移如图所示,则s合=2scos,则F对物体做功W=Fs合cos=2Fscos2由数学知识可知:2Fscos2=Fs(1+cosθ)。
5.【答案】BD
【解析】撤去F后,在物体离开弹簧的过程中,弹簧弹力是变力,物体先做变加速运动,离开弹簧之后做匀减速运动,故A错;刚开始时,由kx0-μmg=ma可知B正确;离开弹簧之后做匀减速运动,减速时间满足3x0=a1t2,a1=μg则t=,C错;速度最大时合力为零,此时弹簧弹力F=μmg=kx,x=,所以物体开始向左运动到速度最大的过程中克服摩擦力做的功为Wf=μmg(x0-x)=μmg(x0-),D正确。
6.【答案】B
【解析】方法一 由图可知F在整个过程中做功分为三个小过程,分别做功为
W1=2×2 J=4 J,W2=-1×2 J=-2 J
W3=4×4 J=16 J,
所以W=W1+W2+W3=4 J+(-2)J+16 J=18 J。
方法二 F-x图象中图线与x轴所围成的面积表示做功的多少,x轴上方为正功,下方为负功,总功取三部分的代数和,即(2×2-2×1+4×4)J=18 J,B正确。
7.【答案】(1)-3 000 J (2)-1 000 J (3)0
【解析】物体受力情况如图所示
(1)WG=-mgLsinθ=-3 000 J
(2)Ff=μFN=μmgcosθ
Wf=-FfL=-μmgcosθ·L
=-1 000 J
(3)解法一:WF=FL=4 000 J
W=WF+WG+Wf=0
解法二:物体做匀速运动,F合=0
故W=0。
功率及机车启动问题同步练习
(答题时间:30分钟)
1. 水平面上一质量为m的物体,在水平力F作用下开始加速运动,力F的功率P保持恒定,运动过程所受的阻力Ff大小不变,物体速度最终达到稳定值vm,F作用过程物体的速度v的倒数与加速度a的关系图象如图所示,仅在已知功率P的情况下,根据图象所给的信息( )
A. 可求出m,Ff和vm
B. 不能求出m
C. 不能求出Ff
D. 可求出加速运动时间
2. 起重机将质量为m的货物由静止开始以加速度a匀加速提升,在t时间内上升h高度,设在t时间内起重机对货物的拉力做的功为W、平均功率为,则( )
A. W=mah
B. W=mgh
C. =
D. =
3. 一辆质量为m的轿车,在平直公路上运行,启动阶段轿车牵引力保持不变,而后以额定功率继续行驶,经过一定时间,其速度由零增大到最大值vm,若所受阻力恒为Ff。则关于轿车的速度v、加速度a、牵引力F、功率P的图象正确的是( )
A. B.
C. D.
4. 如图所示为某汽车在平直公路上启动时发动机功率P随时间t变化的图象,P0为发动机的额定功率。已知在t2时刻汽车的速度已经达到最大vm,汽车所受阻力不变。由此可得( )
A. 在t3时刻,汽车速度一定等于vm
B. 在t1~t2时间内,汽车一定做匀速运动
C. 在t2~t3时间内,汽车一定做匀速运动
D. 在发动机功率达到额定功率前,汽车一定做匀加速运动
5. 质量为m=5.0×106kg的列车以恒定不变的功率由静止沿平直轨道加速行驶,当速度增大到v1=2 m/s时,加速度a1=0.9 m/s2,当速度增大到v2=10 m/s时,加速度a2=0.1 m/s2,如果列车所受阻力大小不变,求:
(1)列车所受阻力是多少?
(2)在该功率下列车的最大速度是多少?
6. 质量为2 000 kg、额定功率为80 kW的汽车,在平直公路上行驶中的最大速度为20 m/s。若汽车从静止开始做匀加速直线运动,加速度大小为2 m/s2,运动中的阻力不变。求:
(1)汽车所受阻力的大小;
(2)3 s末汽车的瞬时功率;
(3)汽车做匀加速运动的时间;
(4)汽车在匀加速运动中牵引力所做的功;
功率及机车启动问题同步练习参考答案
1.【答案】A
【解析】当加速度为零时,物体做匀速运动,此时的牵引力等于阻力,速度为最大值;由功率的计算公式可得P=Fv,而F-Ff=ma,联立可得=a+,由图象可得斜率为,因此可求出m、Ff和vm,故A正确;物体做变加速运动,加速运动的时间不可求,故D错误。
2.【答案】D
【解析】对货物进行受力分析,货物受重力和起重机对货物的拉力F,根据牛顿第二定律得:F-mg=ma,解得:F=m(a+g),上升h高度,起重机对货物拉力做功W=Fh=m(a+g)h,故A、B错误;由于货物做匀加速运动,平均速度等于过程中的中间时刻速度,所以在t时间内的平均速度为=at,起重机对货物拉力做功平均功率为=F=ma(a+g)t,故C错误,D正确。
3.【答案】ACD
【解析】由于启动阶段轿车受到的牵引力不变,加速度不变,所以轿车在开始阶段做匀加速运动,当实际功率达到额定功率时,功率不增加了,再增加速度,就须减小牵引力,当牵引力减小到等于阻力时,加速度等于零,速度达到最大值vm==,所以A、C、D正确,B错误。
4.【答案】AC
【解析】已知在t2时刻汽车的速度已经达到最大vm,此后汽车做匀速直线运动,速度不变,所以在t3时刻,汽车速度一定等于vm,故A正确;0~t1时间内汽车的功率均匀增加,汽车所受阻力不变,牵引力不变,汽车做匀加速直线运动;汽车的功率在t1时刻达到额定功率,根据P=Fv,速度继续增大,牵引力减小,加速度减小,则在t1~t2时间内汽车做加速度减小的加速运动,故B错误;在t2~t3时间内,汽车已达到最大速度,且功率保持不变,汽车一定做匀速直线运动,故C正确;由此分析知,在发动机功率达到额定功率前,汽车先做匀加速运动,后做加速度减小的变加速运动,故D错误。
5.【答案】(1)5.0×105N (2)20 m/s
【解析】(1)设列车恒定不变的功率为P,大小不变的阻力为Ff,当列车速度增大到v1=2 m/s时,P=F1v1①
由牛顿第二定律可得:F1-Ff=ma1②
当列车速度增大到v2=10 m/s时,P=F2v2③
由牛顿第二定律可得:F2-Ff=ma2④
将①、③分别代入②、④联立方程可解得:
P=1.0×107W,Ff=5.0×105N
(2)该功率下列车以最大速度行驶时,牵引力等于阻力,有P=Fvm=Ffvm
解得vm==20 m/s。
6.【答案】(1)4 000 N (2)4.8×104W (3)5 s (4)2×105J
【解析】(1)以最大速度行驶时,根据P=Fv,得F=4 000 N。而此时牵引力和阻力大小相等。
(2)3 s时的速度v=at=6m/s,而牵引力由F-Ff=ma得F=8 000 N,故此时的功率为P=Fv=4.8×104W。
(3)设匀加速运动的时间为t,则t时刻的速度为v=at,这时汽车的功率为额定功率。由P=Fv,将F=8 000 N和v=at代入得t=5 s。
(4)匀加速运动阶段牵引力为恒力,牵引力所做的功W=Fl=Fat2=8000××2×52J=2×105J
