人教版七年级数学下册5.1.3同位角、内错角、同旁内角 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册5.1.3同位角、内错角、同旁内角 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 378.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 16:41:58 | ||
图片预览




文档简介
5.1.3同位角、内错角、同旁内角
同步练习
一、单选题
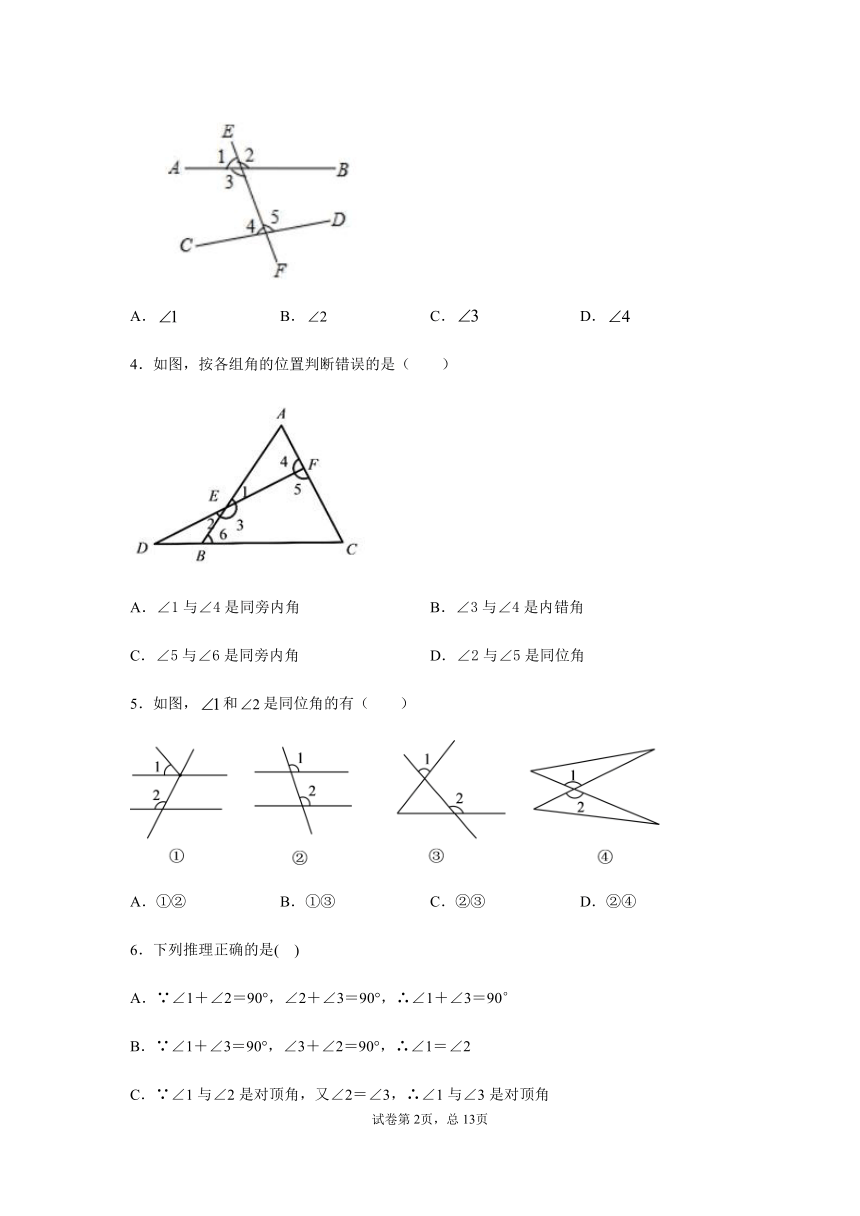
1.如图,和不是同旁内角的是(
)
A.
B.
C.
D.
2.下列所示的四个图形中,∠1和∠2是同位角的是(
)
A.②③
B.①②③
C.①②④
D.①④
3.如图,的同位角是(
)
A.
B.
C.
D.
4.如图,按各组角的位置判断错误的是(
)
A.∠1与∠4是同旁内角
B.∠3与∠4是内错角
C.∠5与∠6是同旁内角
D.∠2与∠5是同位角
5.如图,和是同位角的有(
)
A.①②
B.①③
C.②③
D.②④
6.下列推理正确的是(
)
A.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1+∠3=90°
B.∵∠1+∠3=90°,∠3+∠2=90°,∴∠1=∠2
C.∵∠1与∠2是对顶角,又∠2=∠3,∴∠1与∠3是对顶角
D.∵∠1与∠2是同位角,又∠2与∠3是同位角,∴∠1与∠3是同位角
7.如图,直线,被直线所截,则与是(
)
A.同位角
B.内错角
C.同旁内角
D.对顶角
8.如图,直线AB,CD被直线EF所截,与AB,CD分别交于点E,F,下列描述:
①∠1和∠2互为同位角
②∠3和∠4互为内错角
③∠1=∠4
④∠4+∠5=180°
其中,正确的是(
)
A.①③
B.②④
C.②③
D.③④
9.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2
B.∠2,∠6
C.∠5,∠4
D.∠2,∠4
10.如图,∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
11.如图所示,下列说法不正确的是(
)
A.∠1和∠2是同旁内角
B.∠1和∠3是对顶角
C.∠3和∠4是同位角
D.∠1和∠4是内错角
12.如图,直线a,b被直线c所截,则下列说法中错误的是(
)
A.∠1与∠2是邻补角
B.∠1与∠3是对顶角
C.∠2与∠4是同位角
D.∠3与∠4是内错角
13.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)不相等的两个角不是同位角;
(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(4)从直线外一点到这条直线的垂线段,叫做该点到直线的距离;
(5)过一点作已知直线的平行线,有且只有一条.
其中真命题的有(
)
A.0个
B.1个
C.2个
D.3个
14.如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A.30°
B.140°
C.50°
D.60°
15.如图的四个图中,∠1与∠2是同位角的有(
)
A.②③
B.①②③
C.①
D.①②④
二、填空题
16.如图,∠1和∠3是直线______
和______
被直线______
所截而成的______
角;图中与∠2是同旁内角的角有______
个.
17.如图,直线AF和AC被直线EB所截,∠EBC的同位角是∠EOF,直线DC、AC被直线AF所截,∠FAC同位角是_____.
18.如图所示,同位角有对,内错角有对,同旁内角有对,则的值是____________
19.如图,∠B的同位角是_____.
20.如图,直线AB、CD被直线EF所截,则∠1的内错角是______.
三、解答题
21.如图:∠1和∠4是AB、_______被_______所截得的________角,∠3和∠5是_______、_____被_______所截得的_________角,∠2和∠5是______、_______被_______所截得的________角,AC、BC被AB所截得的同旁内角是________.
22.完成下面的证明:
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD
(已知)
∴∠2=_________(
)
又∵∠1=∠3
∴∠3=∠_________(
)
∴BC//__________(
)
∴∠B+________=180°(
)
又∵∠B=50°
∴∠BDE=130°.
23.在同一个“三线八角”的基本图形中,如果已知一对内错角相等.
(1)图中其余的各对内错角相等吗?为什么?
(2)图中的各对同位角相等吗?为什么?
(3)猜想图中各对同旁内角有怎样的数量关系.
24.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
25.如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=
∠COF.
(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
参考答案
1--10DCACC
BACBD
ADBBD
16.AB
AC
DE
内错
3
17.∠COF.
18.6
19.∠DCF
20.∠3.
21.CD,
BE,
同位;
AB,
BC,
AC,
同旁内
AB,
CD,
AC,
内错;
∠4和∠5
试题解析:∠1和∠4是AB、CD被BE所截得的同位角,
∠3和∠5是BC、AB被AC所截得的同旁内角,
∠2和∠5是AB、CD被AC所截得的内错角,
AC、BC被AB所截得的同旁内角是∠4和∠5.
22.∠1;两直线平行,同位角相等;∠2;等量代换;DE;内错角相等,两直线平行;∠BDE;两直线平行,同旁内角互补
解:∵FG//CD?(已知)
∴∠2=∠1(两直线平行,同位角相等)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//DE(内错角相等,两直线平行)
∴∠B+∠BDE=180°(两直线平行,同旁内角互补)
又∵∠B=50°
∴∠BDE=130°.
故答案为:∠1;两直线平行,同位角相等;∠2;等量代换;DE;内错角相等,两直线平行;∠BDE;两直线平行,同旁内角互补.
23.(1)相等;
(2)相等;
(3)互补.
理由如下:
如图,
(1)由∠1=∠2,又∠3=∠4(等角的补角相等);
(2)
由∠1=∠2,
又∠1=∠5(对顶角相等),所以∠2=∠5,
同理可得:其他对同位角也相等;
(3)由∠1=∠2,又∠1+∠3=180°,所以∠2+∠3=180°(等量代换),
同理:∠1+∠4=180°.
24.(1)2;(2)6;(3)24;(4)
(1)如图
其中同旁内角有与,与,共2对
(2)如图
其中同旁内角有与,与,与,与,与,与,共6对,
(3)如图
其中的同位角有与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,
与,与,与,与,与,与,与,与共24对,
(4)根据以上规律,平面内条直线两两相交,最多可以形成对同旁内角
25.(1)60°(2)∠BMF(3)30°
(1)解:∵∠COM=120°,
∴∠DOF=120°,
∵OG平分∠DOF,
∴∠FOG=60°
(2)解:与∠FOG互为同位角的角是∠BMF
(3)解:∵∠COM=120°,
∴∠COF=60°,
∵∠EMB=
∠COF,
∴∠EMB=30°,
∴∠AMO=30°
试卷第1页,总3页
试卷第1页,总3页
同步练习
一、单选题
1.如图,和不是同旁内角的是(
)
A.
B.
C.
D.
2.下列所示的四个图形中,∠1和∠2是同位角的是(
)
A.②③
B.①②③
C.①②④
D.①④
3.如图,的同位角是(
)
A.
B.
C.
D.
4.如图,按各组角的位置判断错误的是(
)
A.∠1与∠4是同旁内角
B.∠3与∠4是内错角
C.∠5与∠6是同旁内角
D.∠2与∠5是同位角
5.如图,和是同位角的有(
)
A.①②
B.①③
C.②③
D.②④
6.下列推理正确的是(
)
A.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1+∠3=90°
B.∵∠1+∠3=90°,∠3+∠2=90°,∴∠1=∠2
C.∵∠1与∠2是对顶角,又∠2=∠3,∴∠1与∠3是对顶角
D.∵∠1与∠2是同位角,又∠2与∠3是同位角,∴∠1与∠3是同位角
7.如图,直线,被直线所截,则与是(
)
A.同位角
B.内错角
C.同旁内角
D.对顶角
8.如图,直线AB,CD被直线EF所截,与AB,CD分别交于点E,F,下列描述:
①∠1和∠2互为同位角
②∠3和∠4互为内错角
③∠1=∠4
④∠4+∠5=180°
其中,正确的是(
)
A.①③
B.②④
C.②③
D.③④
9.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2
B.∠2,∠6
C.∠5,∠4
D.∠2,∠4
10.如图,∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
11.如图所示,下列说法不正确的是(
)
A.∠1和∠2是同旁内角
B.∠1和∠3是对顶角
C.∠3和∠4是同位角
D.∠1和∠4是内错角
12.如图,直线a,b被直线c所截,则下列说法中错误的是(
)
A.∠1与∠2是邻补角
B.∠1与∠3是对顶角
C.∠2与∠4是同位角
D.∠3与∠4是内错角
13.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)不相等的两个角不是同位角;
(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(4)从直线外一点到这条直线的垂线段,叫做该点到直线的距离;
(5)过一点作已知直线的平行线,有且只有一条.
其中真命题的有(
)
A.0个
B.1个
C.2个
D.3个
14.如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A.30°
B.140°
C.50°
D.60°
15.如图的四个图中,∠1与∠2是同位角的有(
)
A.②③
B.①②③
C.①
D.①②④
二、填空题
16.如图,∠1和∠3是直线______
和______
被直线______
所截而成的______
角;图中与∠2是同旁内角的角有______
个.
17.如图,直线AF和AC被直线EB所截,∠EBC的同位角是∠EOF,直线DC、AC被直线AF所截,∠FAC同位角是_____.
18.如图所示,同位角有对,内错角有对,同旁内角有对,则的值是____________
19.如图,∠B的同位角是_____.
20.如图,直线AB、CD被直线EF所截,则∠1的内错角是______.
三、解答题
21.如图:∠1和∠4是AB、_______被_______所截得的________角,∠3和∠5是_______、_____被_______所截得的_________角,∠2和∠5是______、_______被_______所截得的________角,AC、BC被AB所截得的同旁内角是________.
22.完成下面的证明:
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD
(已知)
∴∠2=_________(
)
又∵∠1=∠3
∴∠3=∠_________(
)
∴BC//__________(
)
∴∠B+________=180°(
)
又∵∠B=50°
∴∠BDE=130°.
23.在同一个“三线八角”的基本图形中,如果已知一对内错角相等.
(1)图中其余的各对内错角相等吗?为什么?
(2)图中的各对同位角相等吗?为什么?
(3)猜想图中各对同旁内角有怎样的数量关系.
24.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
25.如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=
∠COF.
(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
参考答案
1--10DCACC
BACBD
ADBBD
16.AB
AC
DE
内错
3
17.∠COF.
18.6
19.∠DCF
20.∠3.
21.CD,
BE,
同位;
AB,
BC,
AC,
同旁内
AB,
CD,
AC,
内错;
∠4和∠5
试题解析:∠1和∠4是AB、CD被BE所截得的同位角,
∠3和∠5是BC、AB被AC所截得的同旁内角,
∠2和∠5是AB、CD被AC所截得的内错角,
AC、BC被AB所截得的同旁内角是∠4和∠5.
22.∠1;两直线平行,同位角相等;∠2;等量代换;DE;内错角相等,两直线平行;∠BDE;两直线平行,同旁内角互补
解:∵FG//CD?(已知)
∴∠2=∠1(两直线平行,同位角相等)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//DE(内错角相等,两直线平行)
∴∠B+∠BDE=180°(两直线平行,同旁内角互补)
又∵∠B=50°
∴∠BDE=130°.
故答案为:∠1;两直线平行,同位角相等;∠2;等量代换;DE;内错角相等,两直线平行;∠BDE;两直线平行,同旁内角互补.
23.(1)相等;
(2)相等;
(3)互补.
理由如下:
如图,
(1)由∠1=∠2,又∠3=∠4(等角的补角相等);
(2)
由∠1=∠2,
又∠1=∠5(对顶角相等),所以∠2=∠5,
同理可得:其他对同位角也相等;
(3)由∠1=∠2,又∠1+∠3=180°,所以∠2+∠3=180°(等量代换),
同理:∠1+∠4=180°.
24.(1)2;(2)6;(3)24;(4)
(1)如图
其中同旁内角有与,与,共2对
(2)如图
其中同旁内角有与,与,与,与,与,与,共6对,
(3)如图
其中的同位角有与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,
与,与,与,与,与,与,与,与共24对,
(4)根据以上规律,平面内条直线两两相交,最多可以形成对同旁内角
25.(1)60°(2)∠BMF(3)30°
(1)解:∵∠COM=120°,
∴∠DOF=120°,
∵OG平分∠DOF,
∴∠FOG=60°
(2)解:与∠FOG互为同位角的角是∠BMF
(3)解:∵∠COM=120°,
∴∠COF=60°,
∵∠EMB=
∠COF,
∴∠EMB=30°,
∴∠AMO=30°
试卷第1页,总3页
试卷第1页,总3页
