1.2 第1课时 直角三角形-2020-2021学年北师大版八年级数学下册课件(15张)
文档属性
| 名称 | 1.2 第1课时 直角三角形-2020-2021学年北师大版八年级数学下册课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 154.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 15:11:31 | ||
图片预览






文档简介
1.2 直角三角形
第1课时 直角三角形的性质与判定
一、复习旧知,引入新课
直角三角形的定义是什么?
有一个角是直角的三角形叫直角三角形。
三角形的内角和的性质是什么?
三角形的内角和等于180°
曾经探索过的直角三角形的哪些性质和判定方法?
直角三角形的性质
1.在直角三角形中,两锐角互余.
2.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形的判定
1.有一个角等于90°的三角形是直角三角形.
2.有两个角互余的三角形是直角三角形
二、情境导入
三、新课讲授
一、直角三角形的性质与判定
问题一:直角三角形的两锐角互余,为什么?
问题二:如果一个三角形有两个角互余,那么这个三角形是直角三角形,为什么?
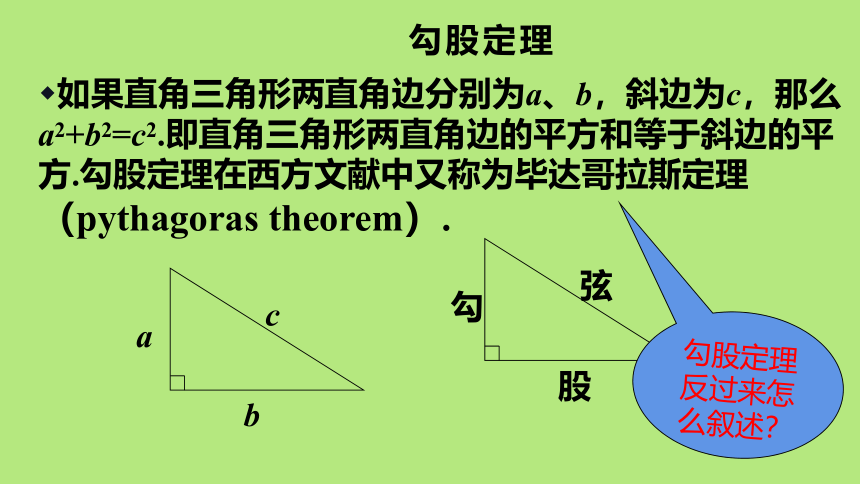
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理(pythagoras theorem).
a
c
b
勾
弦
股
勾股定理反过来怎么叙述?
勾股定理的逆定理
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
已知:如图(1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形.
A
B
C
A
B
C
证明:如图 1-12(2),作 Rt△A′B′C′,使
?? ∠?A′?= 90°,A′B′?= AB,A′C′?= AC,
则 (勾股定理).
∵
∴
∴ BC = B′C′.
∴ △ABC ≌ △A′B′C′ (SSS).
∴ ∠?A = ∠ A′ = 90°(全等三角形的对应角等).
因此,△ABC 是直角三角形.
几何的三种语言
勾股定理的逆定理
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
这是判定直角三角形的根据之一.
在△ABC中
∵AB2+AC2=BC2(已知),
∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形).
a
c
b
B
A
C
命题与逆命题
直角三角形两直角边的平方和等于斜边的平方.
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形
观察上面两个命题,它们的条件与结论之间有怎样的关系?与同伴交流.
再观察下面命题:
如果两个角是对顶角,那么它们相等,
如果两个角相等,那么它们是对顶角;
三角形中相等的边所对的角相等,
三角形中相等的角所对的边相等.
上面每组中两个命题的条件和
结论之间也有类似的关系吗?
与同伴进行交流.
命题与逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,如果把其中一个命题叫做原命题。那么另一个命题称为另一个命题的逆命题.
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?
它们都是真命题吗?
想一想:一个命题是真命题,它逆命题是真命题还是假命题?
定理与逆定理
一个命题是真命题,它逆命题却不一定是真命题.
我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.
你还能举出一些例子吗?
想一想:
互逆命题与互逆定理有何关系?
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
四、 巩固运用、深化拓展
1.直角三角形两锐角的平分线所夹的钝角的度数为( )A.100° B.120° C.135° D.140°
2.符合下列条件的△ABC中,直角三角形的个数为( )①a=3(1),b=4(1),c=5(1); ②a=6,∠A=45°; ③∠A=32°,∠B=58°; ④a=7,b=24,c=25.A.2 B.3 C.4 D.53. 下列说法正确的是( )A.每个命题都有逆命题 B.每个定理都有逆定理C.真命题的逆命题是真命题 D.假命题的逆命题是假命题
4、说出下列合理的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
5.如图,在四边形ABCD中,∠B=90°,AB=BC=3 ,CD=8,AD=10.(1)求∠BCD的度数; (2)求四边形ABCD的面积.
五、课堂小结
定理 直角三角形的两锐角互余
定理 有两个角互余的三角形是直角三角形
勾股定理 直角三角形的两直角边的平方的和等于斜边的平方
勾股定理的逆定理 如果一个三角形的两边的平方的和等于第三边的平方,那么这个三角形是直角三角形
第1课时 直角三角形的性质与判定
一、复习旧知,引入新课
直角三角形的定义是什么?
有一个角是直角的三角形叫直角三角形。
三角形的内角和的性质是什么?
三角形的内角和等于180°
曾经探索过的直角三角形的哪些性质和判定方法?
直角三角形的性质
1.在直角三角形中,两锐角互余.
2.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形的判定
1.有一个角等于90°的三角形是直角三角形.
2.有两个角互余的三角形是直角三角形
二、情境导入
三、新课讲授
一、直角三角形的性质与判定
问题一:直角三角形的两锐角互余,为什么?
问题二:如果一个三角形有两个角互余,那么这个三角形是直角三角形,为什么?
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理(pythagoras theorem).
a
c
b
勾
弦
股
勾股定理反过来怎么叙述?
勾股定理的逆定理
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
已知:如图(1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形.
A
B
C
A
B
C
证明:如图 1-12(2),作 Rt△A′B′C′,使
?? ∠?A′?= 90°,A′B′?= AB,A′C′?= AC,
则 (勾股定理).
∵
∴
∴ BC = B′C′.
∴ △ABC ≌ △A′B′C′ (SSS).
∴ ∠?A = ∠ A′ = 90°(全等三角形的对应角等).
因此,△ABC 是直角三角形.
几何的三种语言
勾股定理的逆定理
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
这是判定直角三角形的根据之一.
在△ABC中
∵AB2+AC2=BC2(已知),
∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形).
a
c
b
B
A
C
命题与逆命题
直角三角形两直角边的平方和等于斜边的平方.
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形
观察上面两个命题,它们的条件与结论之间有怎样的关系?与同伴交流.
再观察下面命题:
如果两个角是对顶角,那么它们相等,
如果两个角相等,那么它们是对顶角;
三角形中相等的边所对的角相等,
三角形中相等的角所对的边相等.
上面每组中两个命题的条件和
结论之间也有类似的关系吗?
与同伴进行交流.
命题与逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,如果把其中一个命题叫做原命题。那么另一个命题称为另一个命题的逆命题.
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?
它们都是真命题吗?
想一想:一个命题是真命题,它逆命题是真命题还是假命题?
定理与逆定理
一个命题是真命题,它逆命题却不一定是真命题.
我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.
你还能举出一些例子吗?
想一想:
互逆命题与互逆定理有何关系?
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
四、 巩固运用、深化拓展
1.直角三角形两锐角的平分线所夹的钝角的度数为( )A.100° B.120° C.135° D.140°
2.符合下列条件的△ABC中,直角三角形的个数为( )①a=3(1),b=4(1),c=5(1); ②a=6,∠A=45°; ③∠A=32°,∠B=58°; ④a=7,b=24,c=25.A.2 B.3 C.4 D.53. 下列说法正确的是( )A.每个命题都有逆命题 B.每个定理都有逆定理C.真命题的逆命题是真命题 D.假命题的逆命题是假命题
4、说出下列合理的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
5.如图,在四边形ABCD中,∠B=90°,AB=BC=3 ,CD=8,AD=10.(1)求∠BCD的度数; (2)求四边形ABCD的面积.
五、课堂小结
定理 直角三角形的两锐角互余
定理 有两个角互余的三角形是直角三角形
勾股定理 直角三角形的两直角边的平方的和等于斜边的平方
勾股定理的逆定理 如果一个三角形的两边的平方的和等于第三边的平方,那么这个三角形是直角三角形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
