1.1 第3课时 等腰三角形-2020-2021学年北师大版八年级数学下册课件(15张)
文档属性
| 名称 | 1.1 第3课时 等腰三角形-2020-2021学年北师大版八年级数学下册课件(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 116.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 00:00:00 | ||
图片预览






文档简介
1.1 等腰三角形
第3课时 等腰三角形的判定与反证法
一、复习旧知,引入新课
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(A点)为目标,然后在这棵树的正南方南岸B点插一小旗作标志,沿南偏东60度方向走一段距离到C处时,测得∠ACB为30度,这时,地质专家测得BC的长度是50米,就可知河流宽度是50米.
这样估测河流宽度的根据是什么吗?他是怎么知道BC的长度是等于河流宽度的呢?
二、情境导入
三、合作探究
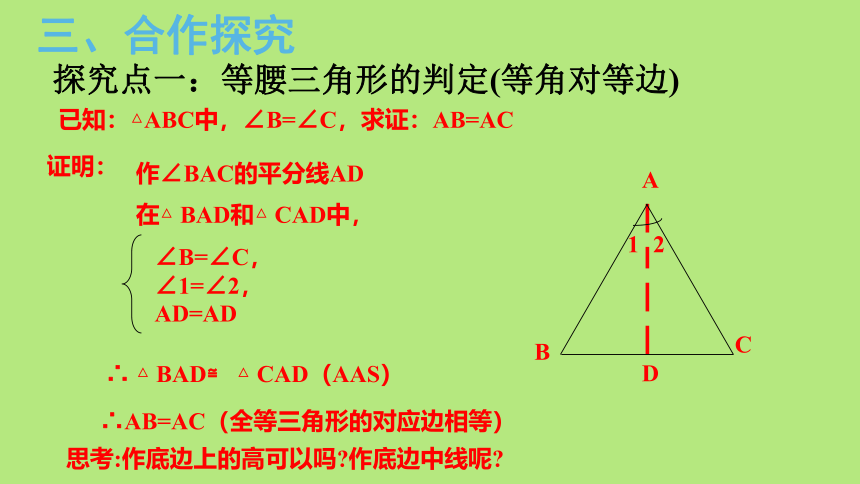
探究点一:等腰三角形的判定(等角对等边)
已知:△ABC中,∠B=∠C,求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠B=∠C,
∠1=∠2,
AD=AD
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
思考:作底边上的高可以吗?作底边中线呢?
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)
A
B
C
应用格式:
在△ABC中
∵ ∠B=∠C
∴ AB=AC (等角对等边)
例1:如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
解:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,
∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的角平分线,
∴∠BAE=∠EAC,
∵∠B+∠BAE=∠AEC,∠ACD+∠EAC=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你认为小明这个结论成立吗?如果成立,你能证明它吗?
小明是这样想的:
如图 ,在△ABC中,已知 ∠ B≠∠?C,此时 AB 与 AC 要么相等,要么不相等.假设 AB = AC,那么根据“等边对等角”定理可得 ∠ C = ∠ B,这与已知条件 ∠ B≠∠ C 相矛盾,因此 AB≠AC.
A
B
C
探究点二:反证法
小明在证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立. 这种
证明方法称为反证法.
反证法
例2:求证:△ABC中不能有两个钝角.
证明:假设△ABC中能有两个钝角,
即∠A<90°,∠B>90°,∠C>90°, 所以∠A+∠B+∠C>180°,
这与三角形的内角和为180°矛盾,
所以假设不成立,
因此原命题正确,即△ABC中不能有两个钝角.
1.等腰三角形的一个内角为70°,它的一腰上的高与底边所夹的角的度数是( )(A)35° (B)20° (C)35 °或 20°(D)无法确定
四、 巩固运用、深化拓展
B
A
D
C
2.已知:如图,AD ∥BC,BD平分∠ABC.求证:AB=AD
证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵BD 平分∠ ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)
3.已知五个正数的和等于 1,用反证法证明:这五个数中至少有一个大于或等于
4.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数.
1.等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(等角对等边). 2.反证法 (1)假设结论不成立; (2)从假设出发推出矛盾; (3)假设不成立,则结论成立.
五、课堂小结
谢谢!
第3课时 等腰三角形的判定与反证法
一、复习旧知,引入新课
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(A点)为目标,然后在这棵树的正南方南岸B点插一小旗作标志,沿南偏东60度方向走一段距离到C处时,测得∠ACB为30度,这时,地质专家测得BC的长度是50米,就可知河流宽度是50米.
这样估测河流宽度的根据是什么吗?他是怎么知道BC的长度是等于河流宽度的呢?
二、情境导入
三、合作探究
探究点一:等腰三角形的判定(等角对等边)
已知:△ABC中,∠B=∠C,求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠B=∠C,
∠1=∠2,
AD=AD
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
思考:作底边上的高可以吗?作底边中线呢?
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)
A
B
C
应用格式:
在△ABC中
∵ ∠B=∠C
∴ AB=AC (等角对等边)
例1:如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
解:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,
∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的角平分线,
∴∠BAE=∠EAC,
∵∠B+∠BAE=∠AEC,∠ACD+∠EAC=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你认为小明这个结论成立吗?如果成立,你能证明它吗?
小明是这样想的:
如图 ,在△ABC中,已知 ∠ B≠∠?C,此时 AB 与 AC 要么相等,要么不相等.假设 AB = AC,那么根据“等边对等角”定理可得 ∠ C = ∠ B,这与已知条件 ∠ B≠∠ C 相矛盾,因此 AB≠AC.
A
B
C
探究点二:反证法
小明在证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立. 这种
证明方法称为反证法.
反证法
例2:求证:△ABC中不能有两个钝角.
证明:假设△ABC中能有两个钝角,
即∠A<90°,∠B>90°,∠C>90°, 所以∠A+∠B+∠C>180°,
这与三角形的内角和为180°矛盾,
所以假设不成立,
因此原命题正确,即△ABC中不能有两个钝角.
1.等腰三角形的一个内角为70°,它的一腰上的高与底边所夹的角的度数是( )(A)35° (B)20° (C)35 °或 20°(D)无法确定
四、 巩固运用、深化拓展
B
A
D
C
2.已知:如图,AD ∥BC,BD平分∠ABC.求证:AB=AD
证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵BD 平分∠ ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)
3.已知五个正数的和等于 1,用反证法证明:这五个数中至少有一个大于或等于
4.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数.
1.等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(等角对等边). 2.反证法 (1)假设结论不成立; (2)从假设出发推出矛盾; (3)假设不成立,则结论成立.
五、课堂小结
谢谢!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
