人教版七年级下册数学5.2《平行线及其判定》同步练习(word含答案)
文档属性
| 名称 | 人教版七年级下册数学5.2《平行线及其判定》同步练习(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 387.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 11:37:02 | ||
图片预览


文档简介
人教版七年级下册数学同步练习5.2《平行线及其判定》
?
1.
在同一平面内两条直线的位置关系可能是????
A.相交或垂直
B.垂直或平行
C.平行或相交
D.平行或相交或重合
2.
过直线外一点作的平行线,可以作(
)条.
A.
B.
C.
D.?
3.
同一平面内,直线与两条平行线,的位置关系是(
)
A.与,平行或相交
B.可能与平行,与相交
C.与,一定都相交
D.同旁内角互补,则两直线平行?
4.
下列推理正确的是(????????)
A.因为,所以
B.因为,所以
C.因为,,所以
D.因为,所以
5.
以下三种沿折叠的方法中,能判定纸带两条边线,互相平行的是(????????)
①如图,展开后测得;
②如图,展开后测得且;
③如图,测得.
A.①③
B.①②③
C.①②
D.②③?
6.
如图所示,点是延长线上的一点,如果添加一个条件,使,那么可添加的条件为
(????????)
A.
B.
C.
D.
7.
如图,在下列条件中,能判断的是???
A.
B.
C.
D.?
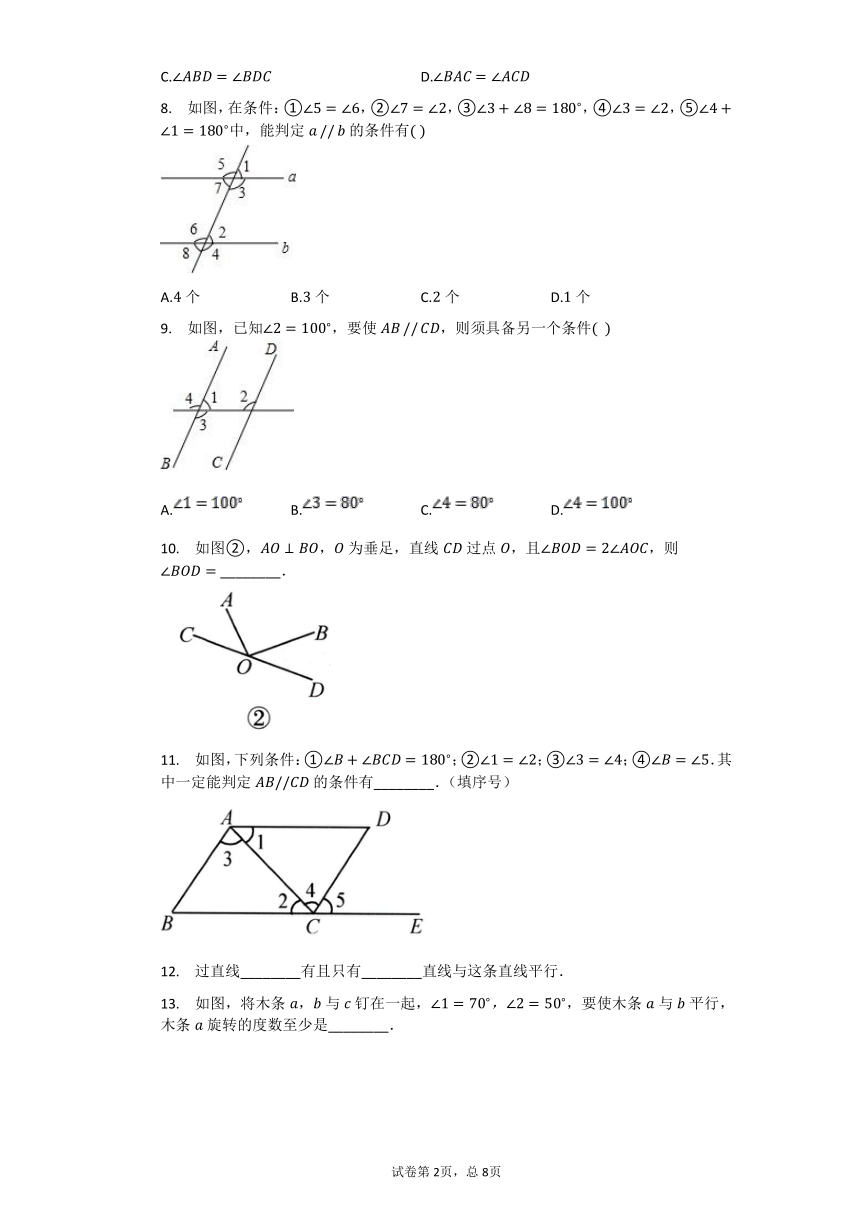
8.
如图,在条件:①,②,③,④,⑤中,能判定的条件有
A.个
B.个
C.个
D.个
9.
如图,已知,要使,则须具备另一个条件??
A.
B.
C.
D.?
10.
如图②,,为垂足,直线过点,且,则?________.
11.
如图,下列条件:①;②;③;④.其中一定能判定的条件有________.(填序号)
?
12.
过直线________有且只有________直线与这条直线平行.
?
13.
如图,将木条,与钉在一起,,要使木条与平行,木条旋转的度数至少是________.
?
14.
画平行线
1.工具:直尺、三角板.
2.方法:一“落”;二“靠”;三“移”;四“画”.
3.请你根据此方法练行线.
已知:直线,点,点.
(1)过点画直线的平行线,能画几条?
(2)过点画直线的平行线,它与过点的平行线平行吗?
?
15.
如图,解答下列问题:
,能得到哪两条直线平行?说明理由.
能否得到?若不能,还需要添加一个什么条件?
?
16.
如图,已知于点,.请你判断直线与位置关系,并证明你的结论.
?
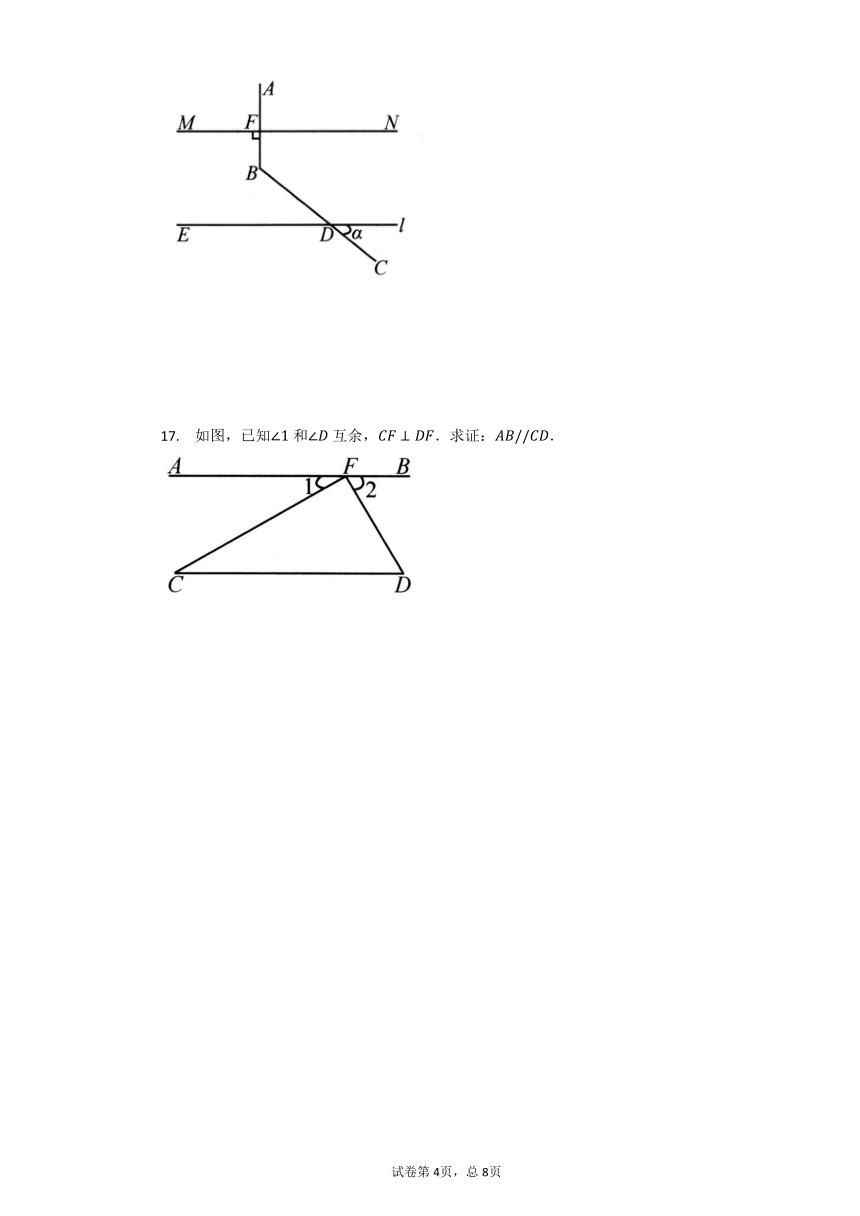
17.
如图,已知和互余,.求证:.
参考答案
人教版七年级下册数学同步练习5.2《平行线及其判定》
一、
选择题
1.
【答案】
C
【解答】
此题暂无解答
2.
【答案】
A
【解答】
解:因为平行公理:过已知直线外一点有且只有一条直线与已知直线平行.
故选.
3.
【答案】
A
【解答】
解:、由于同一平面内两直线的位置关系只有两种:平行和相交,当与平行,根据平行公理的推论可知也与平行;当与相
交,则必然与相交,此选项正确;
、根据的分析可知不可能与平行,而与相交,此选项错误;
、根据的分析,也可能与、都平行,此选项错误;
、若三条直线都平行,也就不存在同旁内角了,此选项错误.
故选.
4.
【答案】
C
【解答】
解:因为平行于同一条直线的两条直线平行,所以选项正确.
故选.
5.
【答案】
C
【解答】
解:①,根据内错角相等,两直线平行进行判定,故正确;
②∵
且,由图可知,,
∴
,
∴
(内错角相等,两直线平行),故正确;
③测得,
∵
与即不是内错角也不是同位角,
∴
不一定能判定两直线平行,故错误.
故选.
6.
【答案】
A
【解答】
解:若,根据“同旁内角互补,两直线平行”,可得出?,正确;,,三项无法根据平行线的判定方法得出?,故选.
7.
【答案】
A
【解答】
解:、,∴
(内错角相等,两直线平行),故正确;
、根据”只能判定“,而非,故错误;
、根据”只能判定,而非,故错误;
、根据“只能判定,而非,故错误;
故选.
8.
【答案】
A
【解答】
根据“同位角相等,两直线平行”,①,符合条件;
根据“内错角相等,两直线平行”,②,符合条件;
根据“同旁内角互补,两直线平行”,③,⑤,符合条件;
④,不符合.
故选
9.
【答案】
D
【解答】
根据“同位角相等,两直线平行”,得,使
其他不符合条件.
故选
二、
填空题
10.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
,
故答案为.
11.
【答案】
①③④
【解答】
解:①,∴
,符合题意;
②,∴
,故本选项错误;
③,∴
,故本选项正确;
④∴
,故本选项正确.
故答案为:①③④.
12.
【答案】
外
一条
【解答】
解:作一条直线,再在这条直线外做出一点,然后可以在这个点上做出无数条线段,就会发现,无论作多少条线段永远只有一条线段与直线,平行,
∴
过直线外一点有且仅有一条直线与这条直线平行,
故答案为:外;一条.
13.
【答案】
【解答】
解:如图,∵
时,,
∴
要使木条a与平行,木条a旋转的度数至少是,
故答案为:.
三、
解答题
14.
【答案】
(1)略
(2)答:平行
【解答】
略
15.
【答案】
解:能得到:.
理由是:内错角相等,两直线平行;
不能得到.
需添加的条件是:.(答案不唯一).
【解答】
解:()理由如下:
∵
是截、所得的内错角,且,
∴
(内错角相等,两直线平行),
(2)不能得到观察图形可知,
当时,
(同位角相等,两直线平行);
当或时,
(同旁内角互补,两直线平行);
当时,
(同位角相等,两直线平行);
综上可知:还需添加的一个条件可以是,,中的任意一个.
?
?
?
?
?
16.
【答案】
解:直线与的位置关系是平行如图:延长交于,
∵
,∴
∵
,∴
.
∴
.
∵
于,∴
,∴
∴
.即直线与的位置关系是平行.
【解答】
略
17.
【答案】
证明:∵
(已知)
∴
(垂直定义)
∴
(平角的定义)
∵
和互余(已知)
∴
(余角的定义)
∴
(同角或等角的余角相等)
∴
(内错角相等,两直线平行)
试卷第2页,总2页
试卷第1页,总1页
?
1.
在同一平面内两条直线的位置关系可能是????
A.相交或垂直
B.垂直或平行
C.平行或相交
D.平行或相交或重合
2.
过直线外一点作的平行线,可以作(
)条.
A.
B.
C.
D.?
3.
同一平面内,直线与两条平行线,的位置关系是(
)
A.与,平行或相交
B.可能与平行,与相交
C.与,一定都相交
D.同旁内角互补,则两直线平行?
4.
下列推理正确的是(????????)
A.因为,所以
B.因为,所以
C.因为,,所以
D.因为,所以
5.
以下三种沿折叠的方法中,能判定纸带两条边线,互相平行的是(????????)
①如图,展开后测得;
②如图,展开后测得且;
③如图,测得.
A.①③
B.①②③
C.①②
D.②③?
6.
如图所示,点是延长线上的一点,如果添加一个条件,使,那么可添加的条件为
(????????)
A.
B.
C.
D.
7.
如图,在下列条件中,能判断的是???
A.
B.
C.
D.?
8.
如图,在条件:①,②,③,④,⑤中,能判定的条件有
A.个
B.个
C.个
D.个
9.
如图,已知,要使,则须具备另一个条件??
A.
B.
C.
D.?
10.
如图②,,为垂足,直线过点,且,则?________.
11.
如图,下列条件:①;②;③;④.其中一定能判定的条件有________.(填序号)
?
12.
过直线________有且只有________直线与这条直线平行.
?
13.
如图,将木条,与钉在一起,,要使木条与平行,木条旋转的度数至少是________.
?
14.
画平行线
1.工具:直尺、三角板.
2.方法:一“落”;二“靠”;三“移”;四“画”.
3.请你根据此方法练行线.
已知:直线,点,点.
(1)过点画直线的平行线,能画几条?
(2)过点画直线的平行线,它与过点的平行线平行吗?
?
15.
如图,解答下列问题:
,能得到哪两条直线平行?说明理由.
能否得到?若不能,还需要添加一个什么条件?
?
16.
如图,已知于点,.请你判断直线与位置关系,并证明你的结论.
?
17.
如图,已知和互余,.求证:.
参考答案
人教版七年级下册数学同步练习5.2《平行线及其判定》
一、
选择题
1.
【答案】
C
【解答】
此题暂无解答
2.
【答案】
A
【解答】
解:因为平行公理:过已知直线外一点有且只有一条直线与已知直线平行.
故选.
3.
【答案】
A
【解答】
解:、由于同一平面内两直线的位置关系只有两种:平行和相交,当与平行,根据平行公理的推论可知也与平行;当与相
交,则必然与相交,此选项正确;
、根据的分析可知不可能与平行,而与相交,此选项错误;
、根据的分析,也可能与、都平行,此选项错误;
、若三条直线都平行,也就不存在同旁内角了,此选项错误.
故选.
4.
【答案】
C
【解答】
解:因为平行于同一条直线的两条直线平行,所以选项正确.
故选.
5.
【答案】
C
【解答】
解:①,根据内错角相等,两直线平行进行判定,故正确;
②∵
且,由图可知,,
∴
,
∴
(内错角相等,两直线平行),故正确;
③测得,
∵
与即不是内错角也不是同位角,
∴
不一定能判定两直线平行,故错误.
故选.
6.
【答案】
A
【解答】
解:若,根据“同旁内角互补,两直线平行”,可得出?,正确;,,三项无法根据平行线的判定方法得出?,故选.
7.
【答案】
A
【解答】
解:、,∴
(内错角相等,两直线平行),故正确;
、根据”只能判定“,而非,故错误;
、根据”只能判定,而非,故错误;
、根据“只能判定,而非,故错误;
故选.
8.
【答案】
A
【解答】
根据“同位角相等,两直线平行”,①,符合条件;
根据“内错角相等,两直线平行”,②,符合条件;
根据“同旁内角互补,两直线平行”,③,⑤,符合条件;
④,不符合.
故选
9.
【答案】
D
【解答】
根据“同位角相等,两直线平行”,得,使
其他不符合条件.
故选
二、
填空题
10.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
,
故答案为.
11.
【答案】
①③④
【解答】
解:①,∴
,符合题意;
②,∴
,故本选项错误;
③,∴
,故本选项正确;
④∴
,故本选项正确.
故答案为:①③④.
12.
【答案】
外
一条
【解答】
解:作一条直线,再在这条直线外做出一点,然后可以在这个点上做出无数条线段,就会发现,无论作多少条线段永远只有一条线段与直线,平行,
∴
过直线外一点有且仅有一条直线与这条直线平行,
故答案为:外;一条.
13.
【答案】
【解答】
解:如图,∵
时,,
∴
要使木条a与平行,木条a旋转的度数至少是,
故答案为:.
三、
解答题
14.
【答案】
(1)略
(2)答:平行
【解答】
略
15.
【答案】
解:能得到:.
理由是:内错角相等,两直线平行;
不能得到.
需添加的条件是:.(答案不唯一).
【解答】
解:()理由如下:
∵
是截、所得的内错角,且,
∴
(内错角相等,两直线平行),
(2)不能得到观察图形可知,
当时,
(同位角相等,两直线平行);
当或时,
(同旁内角互补,两直线平行);
当时,
(同位角相等,两直线平行);
综上可知:还需添加的一个条件可以是,,中的任意一个.
?
?
?
?
?
16.
【答案】
解:直线与的位置关系是平行如图:延长交于,
∵
,∴
∵
,∴
.
∴
.
∵
于,∴
,∴
∴
.即直线与的位置关系是平行.
【解答】
略
17.
【答案】
证明:∵
(已知)
∴
(垂直定义)
∴
(平角的定义)
∵
和互余(已知)
∴
(余角的定义)
∴
(同角或等角的余角相等)
∴
(内错角相等,两直线平行)
试卷第2页,总2页
试卷第1页,总1页
