人教版数学九年级上册第二十五章--概率初步 复习练习(Word版 含答案)
文档属性
| 名称 | 人教版数学九年级上册第二十五章--概率初步 复习练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 72.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 16:49:57 | ||
图片预览


文档简介
人教版数学九年级上册二十五章--概率初步
复习练习
一、选择题
不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是
A.
B.
C.
D.
平行四边形ABCD中,AC、BD是两条对角线,现从以下四个关系;;;中随机取出一个作为条件,即可推出平行四边形ABCD是菱形的概率为
A.
B.
C.
D.
1
下列事件中,是必然事件的是
A.
掷一次骰子,向上一面的点数是6
B.
13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月
C.
射击运动员射击一次,命中靶心
D.
经过有交通信号灯的路口,遇到红灯
以下说法合理的是
A.
小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.
某彩票的中奖概率是,那么买100张彩票一定有5张中奖
C.
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
一个质地均匀的骰子,其六面上分别标有数字1,2,3,4,5,6,投掷一次,朝上的面数字小于4的概率为
A.
B.
C.
D.
经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是
A.
B.
C.
D.
掷两枚普通正六面体骰子,所得点数之和为11的概率为
A.
B.
C.
D.
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近
A.
20
B.
300
C.
500
D.
800
从、、3、4四个数中随机选取两个不同的数,分别记为b、c,则关于x的一元二次方程有一正一负两个实数解的概率为
A.
B.
C.
D.
将五张分别画有等边三角形、平行四边形、矩形、等腰梯形、正六边形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张卡片,图形一定是中心对称图形的概率是
A.
B.
C.
D.
电脑福利彩票中有两种方式“22选5”和“29选7”,若选种号码全部正确则获一等奖,你认为获一等奖机会大的是
A.
“22选5”
B.
“29选7”
C.
一样大
D.
不能确定
下列说法正确的是
A.
掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.
甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是,,则甲的射击成绩较稳定
C.
“明天降雨的概率为”,表示明天有半天都在降雨
D.
了解一批电视机的使用寿命,适合用普查的方式
二、填空题
同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为______.
袋子中装有除颜色外完全相同的n个黄色乒乓球和3个白色乒乓球,从中随机抽取1个,若选中白色乒乓球的概率是,则n的值是______.
柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数n
30
75
130
210
480
856
1250
2300
发芽数m
28
72
125
200
457
814
1187
2185
发芽频率
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是______结果精确到.
对于?ABCD,从以下五个关系式中任取一个作为条件:能判定?ABCD是矩形的概率是??????????.
在一个布袋中装有只有颜色不同的a个小球,其中红球的个数为2,随机摸出一个球记下颜色后再放回袋中,通过大量重复实验后发现,摸到红球的频率稳定于,那么可以推算出a大约是______.
三、计算题
在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
两次取出小球上的数字相同的概率;
两次取出小球上的数字之和大于3的概率.
某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与新型冠状病毒防治与预防知识作答满分100分,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩单位:分进行数据统计、数据分析.
甲
85
80
95
85
90
95
100
65
75
85
90
90
70
100
90
80
80
90
98
75
乙
80
60
80
85
95
65
90
85
100
80
95
75
80
80
70
100
95
75
90
90
填空:甲小区的众数为____,乙小区的中位数为____;
甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
对于此次抽样调查中测试成绩为的居民,社区鼓励他们重新学习,然后从中随机抽取两名居民进行测试,请用列表法或树状图法求刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.
四、解答题
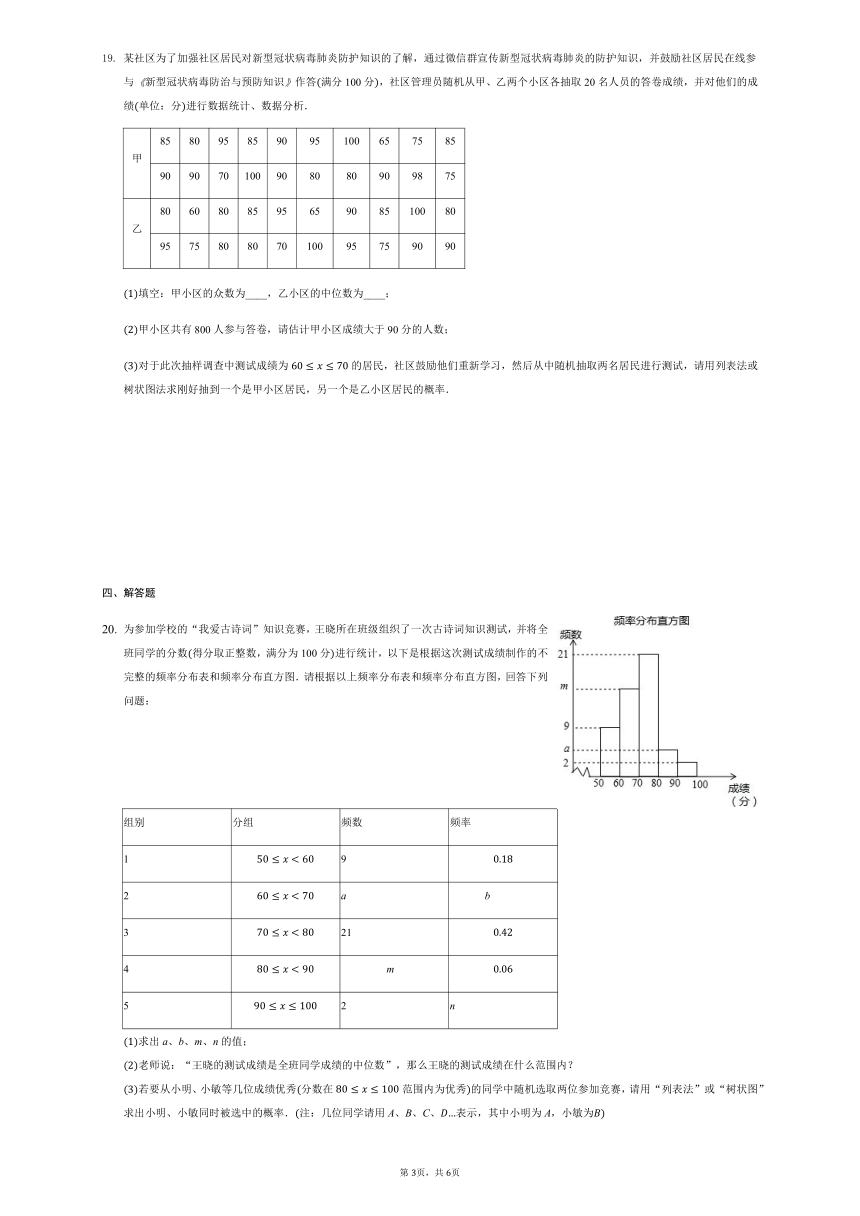
为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数得分取正整数,满分为100分进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
组别
分组
频数
频率
1
9
2
a
???????????
b
3
21
4
???????????????
m
5
2
n
求出a、b、m、n的值;
老师说:“王晓的测试成绩是全班同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
若要从小明、小敏等几位成绩优秀分数在范围内为优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.注:几位同学请用A、B、C、表示,其中小明为A,小敏为
如图,现有一个均匀的转盘被平均分成六等份,分别标有这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字当指针恰好指在分界线上时,不记,重转.
转动转盘,转出的数字大于3的概率是多少;
现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
这三条线段能构成三角形的概率是多少?
这三条线段能构成等腰三角形的概率是多少?注:要求写出各种可能情况
如图,矩形OABC顶点、,直线分别交BA、OA于点D、E,且D为BA中点.
求k的值及此时的面积;
现向矩形内随机投飞镖,求飞镖落在内的概率.若投在边框上则重投
答案
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】C
11.【答案】A
12.【答案】B
13.【答案】
14.【答案】6
15.【答案】
16.【答案】
17.【答案】10
18.【答案】解:画树状图为:
共有9种等可能的结果数,其中两次取出小球上的数字相同的结果数为3,
所以两次取出小球上的数字相同的概率;
两次取出小球上的数字之和大于3的结果数为6,
所以两次取出小球上的数字之和大于3的概率.
19.【答案】解:,;
人.
答:估计甲小区成绩大于90分的人数是200人.
设乙小区三个人编号为A、B、C,甲小区编号为D、E,
则所有可能组合为:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10种,其中刚好抽到一个是甲小区居民,另一个是乙小区居民的情况数为6种,
刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.
20.【答案】解:本次调查的样本容量为:,
,,,;?
样本容量为50,
则样本的中位数是第25、26个数据的平均数,而第25、26个数据均位于范围内,
王晓的测试成绩在范围内;
画树状图为:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为
共有20种等可能的结果,其中小明、小敏同时被选中的结果为2种,
所以小明、小敏同时被选中的概率.
21.【答案】解:转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
;?
转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
这三条线段能构成三角形的概率是;
转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,分别是4,和4,,
这三条线段能构成等腰三角形的概率是?.
22.【答案】解:矩形OABC顶点、,
,
为BA中点,
,,
把点代入得
;
令,得,
,
,,
;
由得,
.
第2页,共2页
第1页,共1页
复习练习
一、选择题
不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是
A.
B.
C.
D.
平行四边形ABCD中,AC、BD是两条对角线,现从以下四个关系;;;中随机取出一个作为条件,即可推出平行四边形ABCD是菱形的概率为
A.
B.
C.
D.
1
下列事件中,是必然事件的是
A.
掷一次骰子,向上一面的点数是6
B.
13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月
C.
射击运动员射击一次,命中靶心
D.
经过有交通信号灯的路口,遇到红灯
以下说法合理的是
A.
小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.
某彩票的中奖概率是,那么买100张彩票一定有5张中奖
C.
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
一个质地均匀的骰子,其六面上分别标有数字1,2,3,4,5,6,投掷一次,朝上的面数字小于4的概率为
A.
B.
C.
D.
经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是
A.
B.
C.
D.
掷两枚普通正六面体骰子,所得点数之和为11的概率为
A.
B.
C.
D.
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近
A.
20
B.
300
C.
500
D.
800
从、、3、4四个数中随机选取两个不同的数,分别记为b、c,则关于x的一元二次方程有一正一负两个实数解的概率为
A.
B.
C.
D.
将五张分别画有等边三角形、平行四边形、矩形、等腰梯形、正六边形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张卡片,图形一定是中心对称图形的概率是
A.
B.
C.
D.
电脑福利彩票中有两种方式“22选5”和“29选7”,若选种号码全部正确则获一等奖,你认为获一等奖机会大的是
A.
“22选5”
B.
“29选7”
C.
一样大
D.
不能确定
下列说法正确的是
A.
掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.
甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是,,则甲的射击成绩较稳定
C.
“明天降雨的概率为”,表示明天有半天都在降雨
D.
了解一批电视机的使用寿命,适合用普查的方式
二、填空题
同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为______.
袋子中装有除颜色外完全相同的n个黄色乒乓球和3个白色乒乓球,从中随机抽取1个,若选中白色乒乓球的概率是,则n的值是______.
柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数n
30
75
130
210
480
856
1250
2300
发芽数m
28
72
125
200
457
814
1187
2185
发芽频率
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是______结果精确到.
对于?ABCD,从以下五个关系式中任取一个作为条件:能判定?ABCD是矩形的概率是??????????.
在一个布袋中装有只有颜色不同的a个小球,其中红球的个数为2,随机摸出一个球记下颜色后再放回袋中,通过大量重复实验后发现,摸到红球的频率稳定于,那么可以推算出a大约是______.
三、计算题
在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
两次取出小球上的数字相同的概率;
两次取出小球上的数字之和大于3的概率.
某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与新型冠状病毒防治与预防知识作答满分100分,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩单位:分进行数据统计、数据分析.
甲
85
80
95
85
90
95
100
65
75
85
90
90
70
100
90
80
80
90
98
75
乙
80
60
80
85
95
65
90
85
100
80
95
75
80
80
70
100
95
75
90
90
填空:甲小区的众数为____,乙小区的中位数为____;
甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
对于此次抽样调查中测试成绩为的居民,社区鼓励他们重新学习,然后从中随机抽取两名居民进行测试,请用列表法或树状图法求刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.
四、解答题
为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数得分取正整数,满分为100分进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
组别
分组
频数
频率
1
9
2
a
???????????
b
3
21
4
???????????????
m
5
2
n
求出a、b、m、n的值;
老师说:“王晓的测试成绩是全班同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
若要从小明、小敏等几位成绩优秀分数在范围内为优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.注:几位同学请用A、B、C、表示,其中小明为A,小敏为
如图,现有一个均匀的转盘被平均分成六等份,分别标有这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字当指针恰好指在分界线上时,不记,重转.
转动转盘,转出的数字大于3的概率是多少;
现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
这三条线段能构成三角形的概率是多少?
这三条线段能构成等腰三角形的概率是多少?注:要求写出各种可能情况
如图,矩形OABC顶点、,直线分别交BA、OA于点D、E,且D为BA中点.
求k的值及此时的面积;
现向矩形内随机投飞镖,求飞镖落在内的概率.若投在边框上则重投
答案
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】C
11.【答案】A
12.【答案】B
13.【答案】
14.【答案】6
15.【答案】
16.【答案】
17.【答案】10
18.【答案】解:画树状图为:
共有9种等可能的结果数,其中两次取出小球上的数字相同的结果数为3,
所以两次取出小球上的数字相同的概率;
两次取出小球上的数字之和大于3的结果数为6,
所以两次取出小球上的数字之和大于3的概率.
19.【答案】解:,;
人.
答:估计甲小区成绩大于90分的人数是200人.
设乙小区三个人编号为A、B、C,甲小区编号为D、E,
则所有可能组合为:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10种,其中刚好抽到一个是甲小区居民,另一个是乙小区居民的情况数为6种,
刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.
20.【答案】解:本次调查的样本容量为:,
,,,;?
样本容量为50,
则样本的中位数是第25、26个数据的平均数,而第25、26个数据均位于范围内,
王晓的测试成绩在范围内;
画树状图为:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为
共有20种等可能的结果,其中小明、小敏同时被选中的结果为2种,
所以小明、小敏同时被选中的概率.
21.【答案】解:转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
;?
转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
这三条线段能构成三角形的概率是;
转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,分别是4,和4,,
这三条线段能构成等腰三角形的概率是?.
22.【答案】解:矩形OABC顶点、,
,
为BA中点,
,,
把点代入得
;
令,得,
,
,,
;
由得,
.
第2页,共2页
第1页,共1页
同课章节目录
