苏科版八年级数学下册教案-11.3 用反比例函数解决问题 (1)
文档属性
| 名称 | 苏科版八年级数学下册教案-11.3 用反比例函数解决问题 (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 66.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 20:37:36 | ||
图片预览

文档简介
课题
11.3用反比例函数解决问题(1)
自主空间
学习目标
1、能利用反比例函数的相关的知识,分析和解决一些简单的实际问题.
2、能根据实际问题中的条件确定反比例函数的解析式.
学习重点
能利用反比例函数的相关的知识分析和解决一些简单的实际问题.
学习难点
根据实际问题中的条件确定反比例函数的解析式.
教学流程
温
故
知
新
反比例函数图像有什么性质?
当K>0时
当K<0时
一、新知探究:
你吃过拉面吗?你知道在做拉面的过程中渗透着数学知识吗?
体积为20cm3的面团做成拉面,面条的总长度y与面条粗细(横截面积)s有怎样的函数关系?如果某家面馆的师傅手艺精湛,他拉的面条粗1mm2,面条总长是多少?
4月踏青的季节,我校组织八年级学生去北山春游,从学校出发到山脚全程约为120千米,
(1)汽车的速度v与时间t有怎样的函数关系?
(2)原计划8点出发,11点到,但为了提前一个小时到达能参观一个活动,平均车速应多快?
二、例题分析:
例1、小明将一篇24000字的社会调查报告录入电脑,打印成文。
(1)如果小明以每分种120字的速度录入,他需要多少时间才能完成录入任务?
(2)录入文字的速度v(字/min)与完成录入的时间t(min)有怎样的函数关系?
(3)小明希望能在3h内完成录入任务,那么他每分钟至少应录入多少个字?
例2某自来水公司计划新建一个容积为的长方形蓄水池。
(1)蓄水池的底部S(平方米)与其深度有怎样的函数关系?
(2)如果蓄水池的深度设计为5m,那么蓄水池的底面积应为多少平方米?
(3)由于绿化以及辅助用地的需要,经过实地测量,蓄水池的长与宽最多只能设计为100m和60m,那么蓄水池的深度至少达到多少才能满足要求?(保留两位小数)
展示交流:
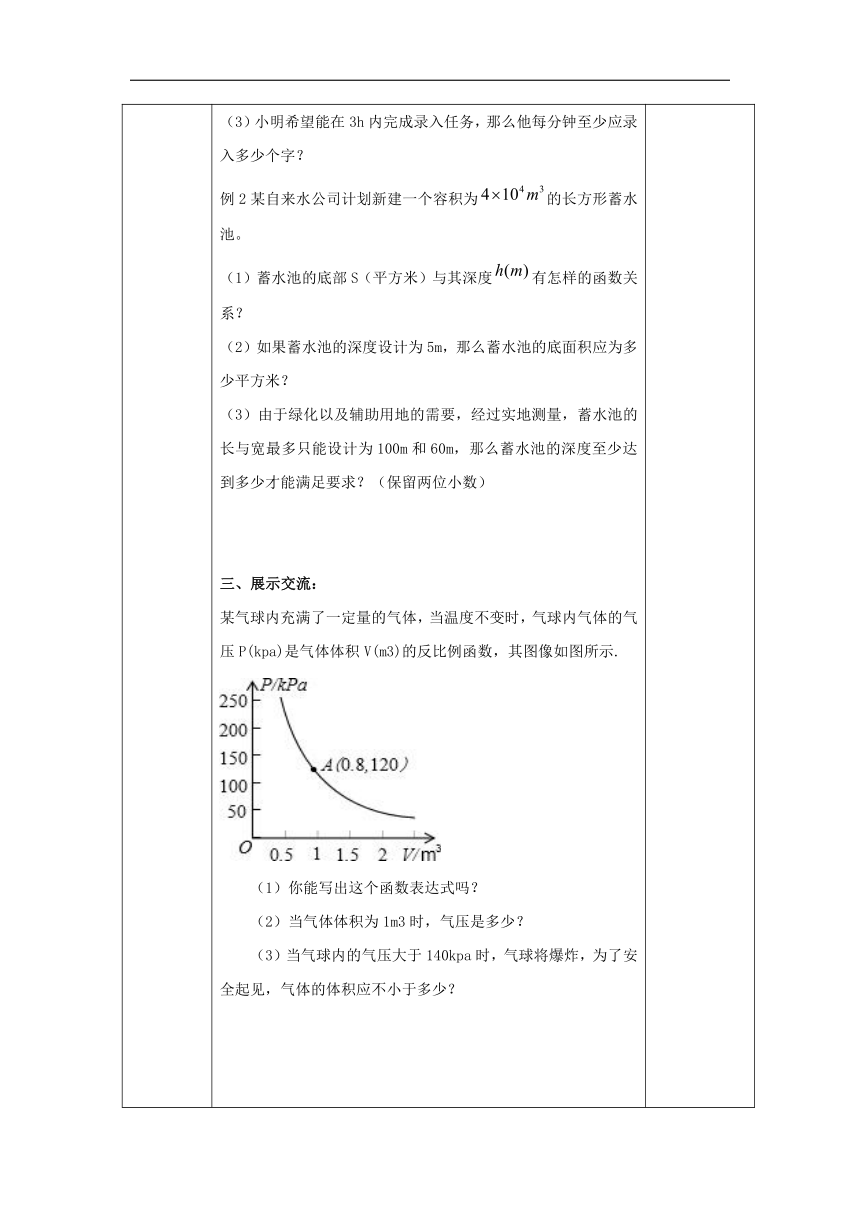
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图像如图所示.
你能写出这个函数表达式吗?
当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kpa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?
四、提炼总结:
1、生活中还有许多反比例函数模型的实际问题,你能举出例子吗?
2、
反比例函数的实际应用,要认真分析题意;注意函数与方程的联系;注重函数的数形结合思想;理解函数的实际意义。
当
堂
达
标
1、下列关系描述与所给的函数图象(如图所示)中,对应正确的是(
)
①矩形的面积一定时,它的两邻边y(cm)与x(cm)之间的关系
②拖拉机工作时,每小时耗油量相同,油箱中余油量y(L)与工作时间x(h)之间的关系
③某城市一天气温y(℃)随时间x(h)变化的关系
④立方体的表面积y(c)与它的边长x(cm)之间的关系.
A.关系①对应乙,②对应丙
B.关系②对应甲,③对应丁
C.关系④对应甲,①对应丁
D.关系③对应丁,④对应乙
2、已知反比例函数y=与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1)求反比例函数的解析式;
(2)求n的值;
(3)求一次函数y=mx+b的解析式.
3、为了预防“非典”,某学校对教室采用药熏消毒法进行消毒,
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x
的函数关系式为:
________,自变量x
的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
学习反思:
11.3用反比例函数解决问题(1)
自主空间
学习目标
1、能利用反比例函数的相关的知识,分析和解决一些简单的实际问题.
2、能根据实际问题中的条件确定反比例函数的解析式.
学习重点
能利用反比例函数的相关的知识分析和解决一些简单的实际问题.
学习难点
根据实际问题中的条件确定反比例函数的解析式.
教学流程
温
故
知
新
反比例函数图像有什么性质?
当K>0时
当K<0时
一、新知探究:
你吃过拉面吗?你知道在做拉面的过程中渗透着数学知识吗?
体积为20cm3的面团做成拉面,面条的总长度y与面条粗细(横截面积)s有怎样的函数关系?如果某家面馆的师傅手艺精湛,他拉的面条粗1mm2,面条总长是多少?
4月踏青的季节,我校组织八年级学生去北山春游,从学校出发到山脚全程约为120千米,
(1)汽车的速度v与时间t有怎样的函数关系?
(2)原计划8点出发,11点到,但为了提前一个小时到达能参观一个活动,平均车速应多快?
二、例题分析:
例1、小明将一篇24000字的社会调查报告录入电脑,打印成文。
(1)如果小明以每分种120字的速度录入,他需要多少时间才能完成录入任务?
(2)录入文字的速度v(字/min)与完成录入的时间t(min)有怎样的函数关系?
(3)小明希望能在3h内完成录入任务,那么他每分钟至少应录入多少个字?
例2某自来水公司计划新建一个容积为的长方形蓄水池。
(1)蓄水池的底部S(平方米)与其深度有怎样的函数关系?
(2)如果蓄水池的深度设计为5m,那么蓄水池的底面积应为多少平方米?
(3)由于绿化以及辅助用地的需要,经过实地测量,蓄水池的长与宽最多只能设计为100m和60m,那么蓄水池的深度至少达到多少才能满足要求?(保留两位小数)
展示交流:
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图像如图所示.
你能写出这个函数表达式吗?
当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kpa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?
四、提炼总结:
1、生活中还有许多反比例函数模型的实际问题,你能举出例子吗?
2、
反比例函数的实际应用,要认真分析题意;注意函数与方程的联系;注重函数的数形结合思想;理解函数的实际意义。
当
堂
达
标
1、下列关系描述与所给的函数图象(如图所示)中,对应正确的是(
)
①矩形的面积一定时,它的两邻边y(cm)与x(cm)之间的关系
②拖拉机工作时,每小时耗油量相同,油箱中余油量y(L)与工作时间x(h)之间的关系
③某城市一天气温y(℃)随时间x(h)变化的关系
④立方体的表面积y(c)与它的边长x(cm)之间的关系.
A.关系①对应乙,②对应丙
B.关系②对应甲,③对应丁
C.关系④对应甲,①对应丁
D.关系③对应丁,④对应乙
2、已知反比例函数y=与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1)求反比例函数的解析式;
(2)求n的值;
(3)求一次函数y=mx+b的解析式.
3、为了预防“非典”,某学校对教室采用药熏消毒法进行消毒,
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x
的函数关系式为:
________,自变量x
的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
学习反思:
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
