2021年中考数学专题复习教案:分类讨论思想(无答案)
文档属性
| 名称 | 2021年中考数学专题复习教案:分类讨论思想(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 71.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览

文档简介
分类讨论思想
一、学习目标:
通过复习能够掌握从问题的实际出发进行分类讨论的思想方法.当问题中存在不确定因素时,能够把被研究的对象分成若干种情况,然后对各种情况逐一进行讨论,最终得以解决整个问题.
重点:从问题的实际出发进行分类讨论
难点:克服思维的片面性,防止漏解
二、引入复习
例:
等腰三角形的一个内角为70°,则其顶角是___
___.
考点解读:根据研究对象的本质属性的差异,将所研究的问题分为不同种类的思想叫做分类思想.将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做分类讨论.
三、引起分类讨论的几个主要原因
1.问题所涉及到的数学概念是分类进行定义的.如|a|的定义分a>0、a=0、a<0三种情况.这种分类讨论题型可以称为概念型.
例1:已知且,则
2.问题中涉及到的数学定理、公式和运算性质、法则有范围或者条件限制,或者是分类给出的.如讨论一次函数y=kx+b(k≠0)的增减性,要分k<0和k>0两种情况.这种分类讨论题型可以称为性质型.
例2:
已知一次函数y=kx+b,当,对应y的值为,则的值(
)
A
.
14
B
.-6
C
.-6或21
D
.-6或14
3.某些不确定的数量、不确定的图形的形状或位置、不确定的结论等,都要通过分类讨论,保证其完整性,使之具有确定性.
例3.在Rt△ABC中,AB=6,BC=8,则这个三角形的外接圆直径是(
)
A
.
5
B
.10
C
.5或4
D
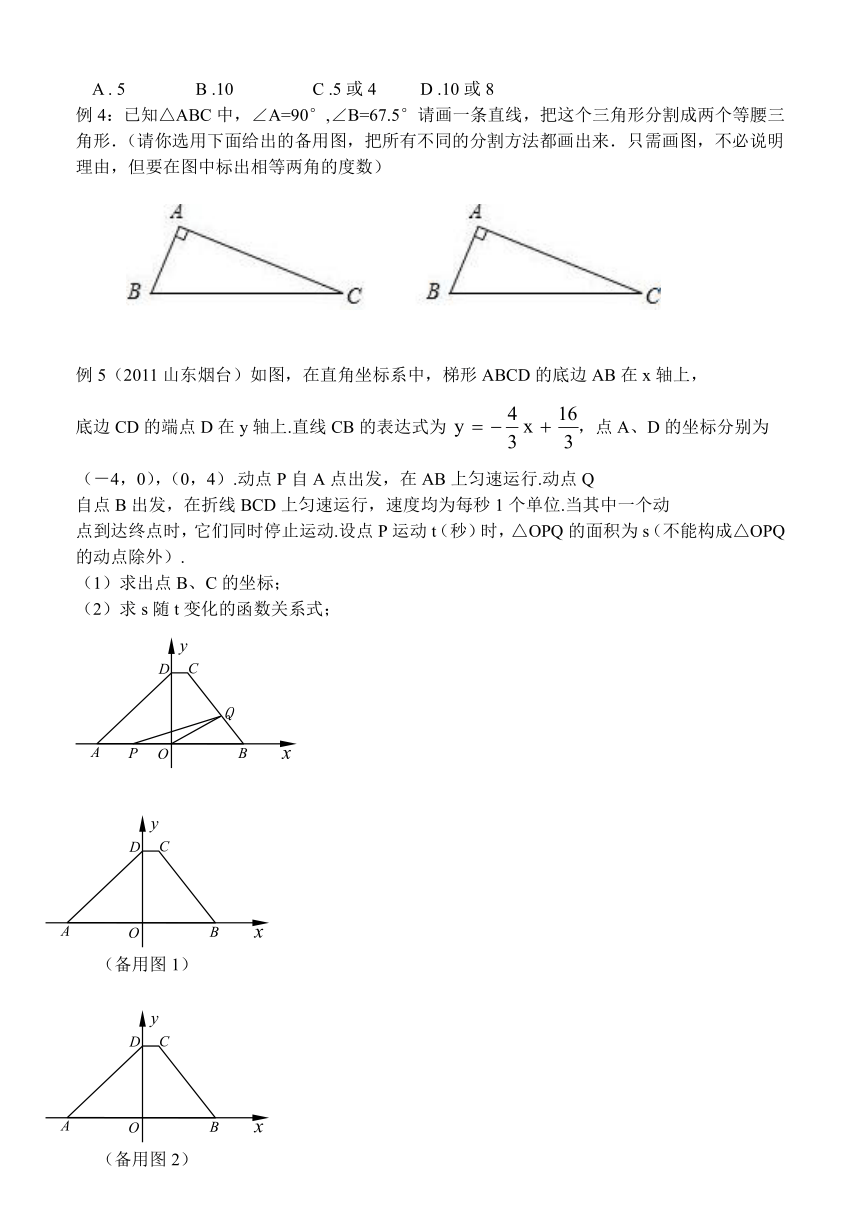
.10或8
例4:已知△ABC中,∠A=90°,∠B=67.5°请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
例5(2011山东烟台)如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,
底边CD的端点D在y轴上.直线CB的表达式为
,点A、D的坐标分别为
(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q
自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动
点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
四、学习体会
五、当堂检测
1.
已知关于x的方程有实数根,求k的取值范围
2.菱形有一内角为120°,有一条对角线为6cm,则此菱形的边长为
cm.
3.五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,则这五个正整数的和为
________
.
4.等腰三角形一腰上的高与另一腰的夹角为45°,则这个等腰三角形的顶角
度
5.
如图已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.若点D在抛物线上,点E在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形.求点D的坐标;
6.已知a、b、c均为非零实数,且满足
则k的值为(
)
A
1
B
-2
C
1或-2
D
1或2
一、学习目标:
通过复习能够掌握从问题的实际出发进行分类讨论的思想方法.当问题中存在不确定因素时,能够把被研究的对象分成若干种情况,然后对各种情况逐一进行讨论,最终得以解决整个问题.
重点:从问题的实际出发进行分类讨论
难点:克服思维的片面性,防止漏解
二、引入复习
例:
等腰三角形的一个内角为70°,则其顶角是___
___.
考点解读:根据研究对象的本质属性的差异,将所研究的问题分为不同种类的思想叫做分类思想.将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做分类讨论.
三、引起分类讨论的几个主要原因
1.问题所涉及到的数学概念是分类进行定义的.如|a|的定义分a>0、a=0、a<0三种情况.这种分类讨论题型可以称为概念型.
例1:已知且,则
2.问题中涉及到的数学定理、公式和运算性质、法则有范围或者条件限制,或者是分类给出的.如讨论一次函数y=kx+b(k≠0)的增减性,要分k<0和k>0两种情况.这种分类讨论题型可以称为性质型.
例2:
已知一次函数y=kx+b,当,对应y的值为,则的值(
)
A
.
14
B
.-6
C
.-6或21
D
.-6或14
3.某些不确定的数量、不确定的图形的形状或位置、不确定的结论等,都要通过分类讨论,保证其完整性,使之具有确定性.
例3.在Rt△ABC中,AB=6,BC=8,则这个三角形的外接圆直径是(
)
A
.
5
B
.10
C
.5或4
D
.10或8
例4:已知△ABC中,∠A=90°,∠B=67.5°请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
例5(2011山东烟台)如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,
底边CD的端点D在y轴上.直线CB的表达式为
,点A、D的坐标分别为
(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q
自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动
点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
四、学习体会
五、当堂检测
1.
已知关于x的方程有实数根,求k的取值范围
2.菱形有一内角为120°,有一条对角线为6cm,则此菱形的边长为
cm.
3.五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,则这五个正整数的和为
________
.
4.等腰三角形一腰上的高与另一腰的夹角为45°,则这个等腰三角形的顶角
度
5.
如图已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.若点D在抛物线上,点E在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形.求点D的坐标;
6.已知a、b、c均为非零实数,且满足
则k的值为(
)
A
1
B
-2
C
1或-2
D
1或2
同课章节目录
