北师大版八年级下册数学3.3中心对称(利用中心对称的性质解决几何问题)(word版含解析)
文档属性
| 名称 | 北师大版八年级下册数学3.3中心对称(利用中心对称的性质解决几何问题)(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 00:00:00 | ||
图片预览



文档简介
利用中心对称的性质解决几何问题
一、选择题
1、如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO.其中错误的结论有多少个( )
A.1个
B.2个
C.3个
D.4个
2、经过矩形的对称中心的任意一条直线把这个矩形分成两部分,设这两部分的面积分别为S1和S2,则S1和S2之间的关系是( )
A.S1>S1
B.S1<S2
C.S1=S2
D.S1和S2的大小关系无法确定
3、如图,△ABC与△A′B′C′是成中心对称,下列说法不正确的是( )
A.S△ABC=S△A′B′C′
B.AB=A′B′,AC=A′C′,BC=B′C′
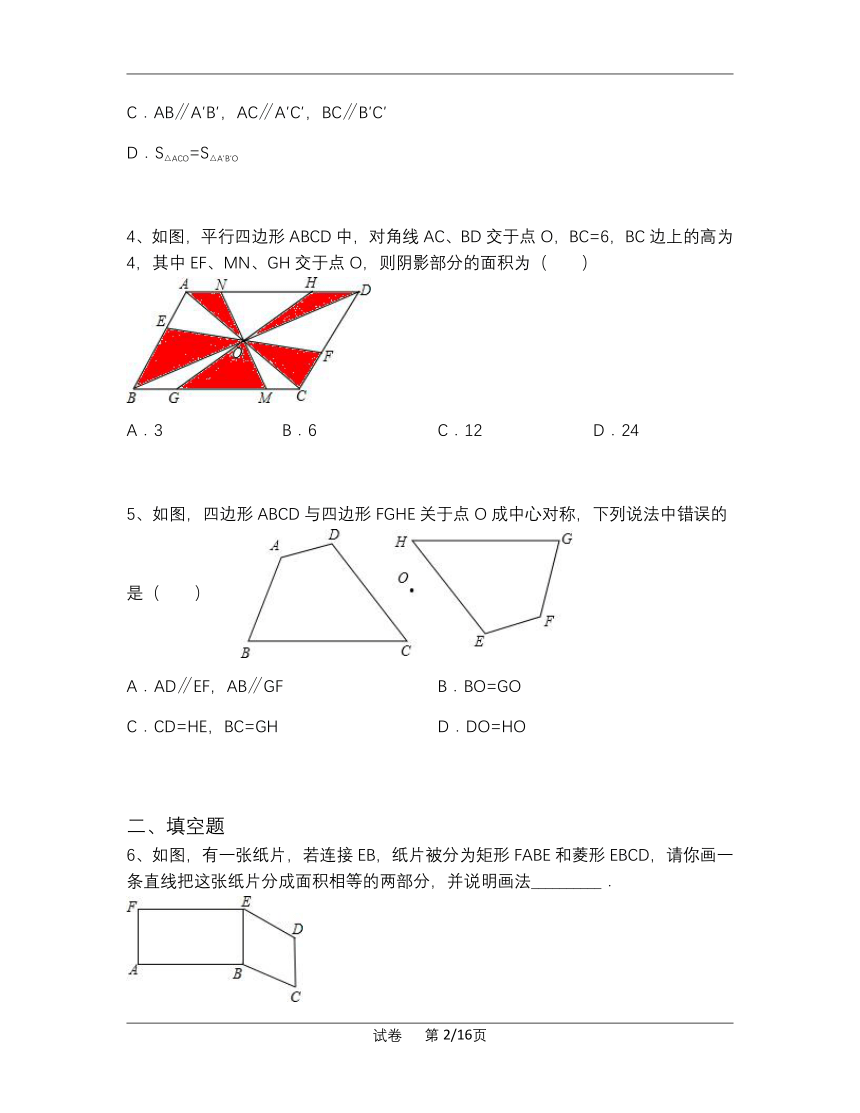
C.AB∥A′B′,AC∥A′C′,BC∥B′C′
D.S△ACO=S△A′B′O
4、如图,平行四边形ABCD中,对角线AC、BD交于点O,BC=6,BC边上的高为4,其中EF、MN、GH交于点O,则阴影部分的面积为( )
A.3
B.6
C.12
D.24
5、如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是( )
A.AD∥EF,AB∥GF
B.BO=GO
C.CD=HE,BC=GH
D.DO=HO
二、填空题
6、如图,有一张纸片,若连接EB,纸片被分为矩形FABE和菱形EBCD,请你画一条直线把这张纸片分成面积相等的两部分,并说明画法__________.
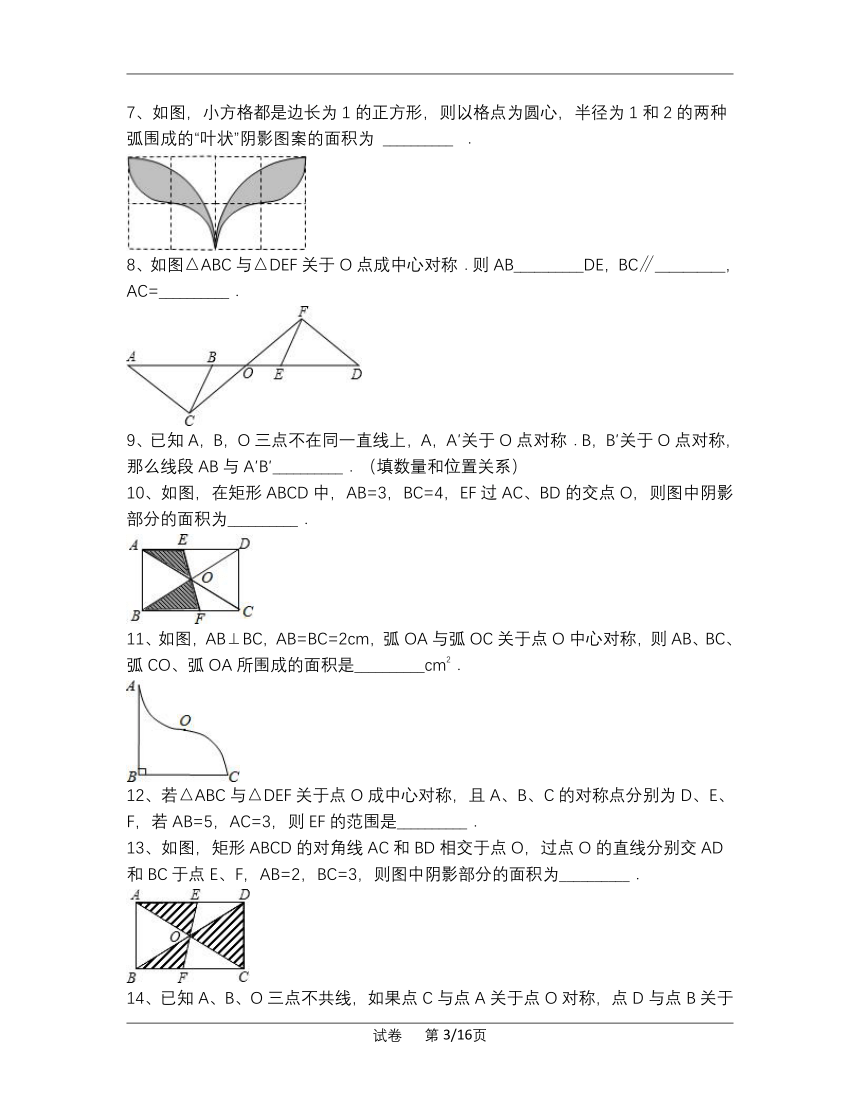
7、如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为
__________
.
8、如图△ABC与△DEF关于O点成中心对称.则AB__________DE,BC∥__________,AC=__________.
9、已知A,B,O三点不在同一直线上,A,A′关于O点对称.B,B′关于O点对称,那么线段AB与A′B′__________.(填数量和位置关系)
10、如图,在矩形ABCD中,AB=3,BC=4,EF过AC、BD的交点O,则图中阴影部分的面积为__________.
11、如图,AB⊥BC,AB=BC=2cm,弧OA与弧OC关于点O中心对称,则AB、BC、弧CO、弧OA所围成的面积是__________cm2.
12、若△ABC与△DEF关于点O成中心对称,且A、B、C的对称点分别为D、E、F,若AB=5,AC=3,则EF的范围是__________.
13、如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为__________.
14、已知A、B、O三点不共线,如果点C与点A关于点O对称,点D与点B关于点O对称,那么线段AB与CD的关系是__________.
15、若线段AB、CD关于点P成中心对称,则线段AB、CD的关系是__________.
16、若矩形的对称中心到两边的距离差为4cm,周长为56cm,则矩形的边长分别为__________.
17、中央电视台大风车栏目图标如图甲,其中心为O,半圆固定,其半径为2r,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆内的轮片面积是不变的(如图乙),这个不变的面积值是
__________
.
18、如图,AB⊥BC,AB=BC=2cm,与关于点O中心对称,则AB、BC、、所围成的图形的面积是__________cm2.
19、如图,过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的__________.
20、如图△ABC与△DEF关于O点成中心对称.则线段BC与EF的关系是__________.
21、如图,线段AB关于点O(不在AB上)的对称线段是A′B′;线段A′B′关于点O′(不在A′B′上)的对称线段是A″B″.那么线段AB与线段A″B″的关系是__________.
三、解答题
22、在平面直角坐标系中,抛物线y=x2+5x+4的顶点为M,与x轴交于A,B两点,与y轴交于C点.
(1)求点A,B,C的坐标;
(2)求抛物线y=x2+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为M′,与x轴交于A′,B′两点,与y轴交于C′点,在以A,B,C,M,A′,B′,C′,M′这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积.
23、如图,在公园里有一块平行四边形的草坪,草坪里有一个圆形花坛,有关部门计划在草坪上修一条小路,这条小路要把草坪和花坛的面积同时平分,请在图中画出这条小路.(小路用AB表示)
24、如图,在四边形ABCD中,AD∥BC,E是CD的中点.
(1)画图:连接AF并延长,交BC的延长线于点F,连接BE;
(2)填空:点A与点F关于点__________成中心对称,若AB=AD+BC,则△ABF是__________三角形,此时点A与点F关于直线__________成轴对称;
(3)图中△__________的面积等于四边形ABCD的面积.
25、如图所示,已知梯形ABCD中,AD∥BC,请你利用中心对称的性质,把梯形ABCD转化成与原梯形面积相等的三角形,并简要说明变换理由.
26、已知:如图所示,E是等腰梯形一腰CD的中点,EF⊥AB,垂足为F,求证:S梯形ABCD=AB?EF.
27、轴对称图形的对称轴将图形面积二等分,中心对称图形过对称中心的直线将图形面积二等分.请用学过的知识将下图所示的图形面积分成相等的两部分.
试卷
第7/16页
利用中心对称的性质解决几何问题的答案和解析
一、选择题
1、答案:
A
试题分析:根据已知对各个结论进行分析从而确定最后的答案.
①正确,根据等底等高可证明S△ADE=S△EOD;
②正确,根据已知及菱形的性质可证明△DEF≌△BEF;
③正确,可证明得△DEO≌△DFO;
④错误,每一条对角线平分一组对角,可得∠ADO=∠CDO,∠EDO=∠FDO,所以∠ADE=∠CDF≠∠EDO;
故选A.
2、答案:
C
试题分析:根据矩形对角线相等且平分的性质,易证△OEC≌△OFA,△DEO≌△BFO,△AOD≌△BOC,即可证明.
试题解析:∵四边形ABCD是矩形,
∴AD=BC,AO=BO=CO=DO,
∴△AOD≌△BOC,
∵∠ECO=∠FAO,OA=OC,∠EOC=∠FOA,
∴△OEC≌△OFA,
同理可证,△DEO≌△BFO,
∴S1=S2.
故选:C.
3、答案:
D
试题分析:根据中心对称图形的性质,即可作出判断.
试题解析:A、根据中心对称的两个图形全等,即可得到,故正确;
B、中心对称图形中,对称点到对称中心的距离相等,故正确;
C、根对称点到对称中心的距离相等,即可证得对应线段平行,故正确;
D、不正确.
故选D.
4、答案:
C
试题分析:由平行四边形的性质易得:△AON≌△COM(AAS),△AOE≌△COF,△BOE≌△DOF,△BOG≌△DOH,继而可证得△GOM≌△HON(SAS),则可得S阴影=S?ABCD.
试题解析:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,AB∥CD,
∴∠OAN=∠OCM,
在△AON和△COM中,
,
∴△AON≌△COM(AAS),
同理:△AOE≌△COF,△BOE≌△DOF,△BOG≌△DOH,
∴OG=OH,OM=ON,
在△GOM和△HON中,
,
∴△GOM≌△HON(SAS),
∴S阴影=S?ABCD=×6×4=12.
故选C.
5、答案:
D
试题分析:根据中心对称的定义和中心对称的性质作答.
试题解析:A、∵AD与EF关于点O成中心对称,∴AD∥EF,同理可得AB∥GF,所以说法正确;
B、∵B与G关于点O成中心对称,∴BO=GO,所以说法正确;
C、∵CD与HE关于点O成中心对称,∴CD=HE,同理可得BC=GH,所以说法正确;
D、∵D与E关于点O成中心对称,∴DO=EO,所以DO=HO错误.
故选D.
二、填空题
6、答案:
试题分析:根据中心对称的性质、菱形和平行四边形是中心对称图形矩形解答即可.
试题解析:如图,连接BF、AE交于M,连接BD、EC交于N,
作直线MN,则直线MN即为所求.
7、答案:
试题分析:连接AB,则阴影部分面积=2(S扇形AOB-S△ABO),依此计算即可求解.
试题解析:
由题意得,阴影部分面积=2(S扇形AOB-S△AOB)=2(-×2×2)=2π-4.
故答案为:2π-4.
8、答案:
试题分析:利用关于某点对称的图形全等,这样可以得出対应边与对应角之间的关系,进而解决.
试题解析:∵△ABC与△DEF关于O点成中心对称
∴△ABC≌△DEF
AB=DE,AC=DF
又∵BO=OE,CO=OF,∠BOC=∠FOE
∴△BOC≌△EOF
∴∠BCO=∠OFE
BC∥EF
故填:=,EF,DF
9、答案:
试题分析:根据中心对称图形对应线段平行且相等的性质填空.
试题解析:中心对称图形中的不在同一直线上的两条对应线段的关系是:平行且相等.
故答案为:平行且相等.
10、答案:
试题分析:易证△AOE≌△COF,则阴影部分的面积为△CDO的面积,根据矩形对角线分成的四部分面积相等,即可计算阴影部分的面积,即可解题.
试题解析:∵AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
则△AOE和△COF面积相等,
∴阴影部分的面积与△CDO的面积相等,
又∵矩形对角线将矩形分成面积相等的四部分,
∴阴影部分的面积为:×3×4=3.
故答案为:3.
11、答案:
试题分析:由弧OA与弧OC关于点O中心对称,根据中心对称的定义,如果连接AC,则点O为AC的中点,则题中所求面积等于△BAC的面积.
连接AC.
∵弧OA与弧OC关于点O中心对称,
∴点O为AC的中点,
∴AB、BC、弧CO、弧OA所围成的面积=△BAC的面积==2cm2.
12、答案:
试题分析:根据成中心对称的两个图形对应线段长相等可知EF的取值范围等于BC的取值范围;
试题解析:∵△ABC与△DEF关于点O成中心对称,且A、B、C的对称点分别为D、E、F,AB=5,AC=3,
∴DE=5,DF=3
∴EF的取值范围为:2<EF<8
故答案为:2<EF<8
13、答案:
试题分析:根据矩形是中心对称图形寻找思路:△OBF≌△ODE,图中阴影部分的面积就是△ADC的面积.
试题解析:根据矩形的性质得△OBF≌△ODE,
属于图中阴影部分的面积就是△ADC的面积.
S△ADC=CD×AD=×2×3=3.
故答案为:3.
14、答案:
试题分析:根据关于点对称的性质得出AO=BO,DO=BO,进而得出四边形ABCD是平行四边形,即可得出答案.
试题解析:∵AO=BO,DO=BO,
∴四边形ABCD是平行四边形,
∴ABCD,
故答案为:ABCD.
15、答案:
试题分析:根据线段AB、CD关于点P成中心对称,再根据中心对称的性质得出对应边之间的关系即可.
试题解析:∵线段AB、CD关于点P成中心对称,
∴线段AB、CD的关系是:平行且相等.
故答案为:平行且相等.
16、答案:
试题分析:如图,设FO=y,EO=x,可以得出2x=AD,2y=AB.可列出两个等式解答即可.
试题解析:设FO=y,EO=x.
故2x=AD,2y=AB.
2×(2x+2y)=56
x-y=4
可得x=5,y=9
所以这个矩形的两邻边长分别为10cm和18cm.
故答案为:10cm,18cm.
17、答案:
试题分析:四个阴影部分的图形正好构成一个中心对称图形,AB过对称中心,根据其中心对称图形的性质,则这个不变的面积是半圆面积的一半,即可求解.
试题解析:这个不变的面积是半圆面积的一半,即××4r2=πr2.
18、答案:
试题分析:连AC,则△ABC为等腰直角三角形,由与关于点O中心对称得到OA=OC,弧OA=弧OC,则弓形OA的面积=弓形OC的面积,因此AB、BC、、所围成的图形的面积=三角形ABC的面积,然后根据直角三角形的面积公式计算即可.
连AC,如图,
∵AB⊥BC,AB=BC=2cm,
∴△ABC为等腰直角三角形,
又∵与关于点O中心对称,
∴OA=OC,弧OA=弧OC,
∴弓形OA的面积=弓形OC的面积,
∴AB、BC、、所围成的图形的面积=三角形ABC的面积=×2×2=2(cm2).
故答案为2.
19、答案:
试题分析:根据矩形的性质,将面积转换后求解即可.
由图可知:OB=OD,∠OBE=∠ODF,∠EOB=∠FOD,
∴△BEO≌△DFO,
∴S△DFO=S△BEO,
∵在△ABO与△AOD中,OB=OD,高相等,
∴S△ABO=S△AOD,
即S△ABO=S△ABD=S?ABCD,
阴影部分的面积=S△AEO+S△DFO=S△AEO+S△BEO=S△ABO=S?ABCD.
故答案为:.
20、答案:
试题分析:根据△ABC与△DEF关于O点成中心对称,得出对应边之间的关系即可得出答案.
试题解析:∵△ABC与△DEF关于O点成中心对称.
∴线段BC与EF的关系是:平行且相等.
故答案为:平行且相等.
21、答案:
试题分析:根据中心对称的概念可知线段AB、A′B′、上的对应点都关于点O对称,A'B'、A''B''上的对应点都关于O'对称.
试题解析:中心对称图形中的不在同一直线上的两条对应线段的关系是:平行且相等.
故线段AB与线段A″B″的关系是:平行且相等.
故答案为:平行且相等.
三、解答题
22、答案:
试题分析:(1)令y=0,求出x的值;令x=0,求出y,即可解答;
(2)先求出A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,-4),再代入解析式,即可解答;
(3)取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,由此判定四边形AMA′M′为平行四边形,又知AA′与MM′不垂直,从而平行四边形AMA′M′不是菱形,过点M作MD⊥x轴于点D,求出抛物线的顶点坐标M,根据,即可解答.
试题解析:(1)令y=0,得x2+5x+4=0,
∴x1=-4,x2=-1,
令x=0,得y=4,
∴A(-4,0),B(-1,0),C(0,4).
(2)∵A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,-4),
∴所求抛物线的函数表达式为y=ax2+bx-4,
将(4,0),(1,0)代入上式,得
解得:,
∴y=-x2+5x-4.
(3)如图,取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,
由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,
∴四边形AMA′M′为平行四边形,
又知AA′与MM′不垂直,
∴平行四边形AMA′M′不是菱形,
过点M作MD⊥x轴于点D,
∵y=,
∴M(),
又∵A(-4,0),A′(4,0)
∴AA′=8,MD=,
∴=
23、答案:
试题分析:利用平行四边形的性质以及圆的性质,得出对角线交点与圆心连线即可平分面积.
试题解析:如图所示:线段AB即为所求.
24、答案:
试题分析:(1)根据要求直接作出图形即可;
(2)利用中心对称的定义回答即可,然后证得AB=BF,利用等腰三角形的性质判定等腰三角形即可;
(3)得到三角形ADE的面积等于三角形ECF的面积,从而得到答案;
试题解析:(1)如图:
(2)∵AD∥BC,
∴∠D=∠DCF,
∵DE=CE,∠AED=∠FEC
在△ADE与△FCE中,
∴△ADE≌△FCE(ASA),
∴AE=FE,AD=CF,
∴点A与点F关于点E成中心对称,
∵若AB=AD+BC,
∴AB=BF,
则△ABF是等腰三角形,此时点A与点F关于直线BE成轴对称;
(3)图中△ABFD?面积等于四边形ABCD的面积.
故答案为:E,等腰,BE,ABF.
25、答案:
试题分析:根据中心对称图形的性质以及全等三角形的判定与性质得出即可.
解;取CD中点M,连接AM并延长交BC延长线于点N,得到△ABN即为与原梯形面积相等的三角形.
在△ADM和△NCM中
,
∴△ADM≌△NCM(ASA),
△NCM可以看作是△ADM关于点M的中心对称图形,
∴△ABN即为与原梯形面积相等的三角形.
26、答案:
试题分析:连接AE交BC的延长线于G点,则梯形ABCD的面积就是△ABE的面积的2倍,则问题就可以比较容易求解.
试题解析:证明:如图,连接AE交BC的延长线于G点,连接BE,
∵AD∥CG,
∴∠D=∠ECG,
在△ADE和△GCE中
∴△ADE≌△GCE(ASA),
∴AE=GE,
∴可得:S△ABG=S梯形ABCD=2S△ABE=AB×FE.
27、答案:
试题分析:利用轴对称图形的对称轴将图形面积二等分,中心对称图形过对称中心的直线将图形面积二等分.分别得出图形的对称轴与对称中心即可得出答案.
试题解析:
一、选择题
1、如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO.其中错误的结论有多少个( )
A.1个
B.2个
C.3个
D.4个
2、经过矩形的对称中心的任意一条直线把这个矩形分成两部分,设这两部分的面积分别为S1和S2,则S1和S2之间的关系是( )
A.S1>S1
B.S1<S2
C.S1=S2
D.S1和S2的大小关系无法确定
3、如图,△ABC与△A′B′C′是成中心对称,下列说法不正确的是( )
A.S△ABC=S△A′B′C′
B.AB=A′B′,AC=A′C′,BC=B′C′
C.AB∥A′B′,AC∥A′C′,BC∥B′C′
D.S△ACO=S△A′B′O
4、如图,平行四边形ABCD中,对角线AC、BD交于点O,BC=6,BC边上的高为4,其中EF、MN、GH交于点O,则阴影部分的面积为( )
A.3
B.6
C.12
D.24
5、如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是( )
A.AD∥EF,AB∥GF
B.BO=GO
C.CD=HE,BC=GH
D.DO=HO
二、填空题
6、如图,有一张纸片,若连接EB,纸片被分为矩形FABE和菱形EBCD,请你画一条直线把这张纸片分成面积相等的两部分,并说明画法__________.
7、如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为
__________
.
8、如图△ABC与△DEF关于O点成中心对称.则AB__________DE,BC∥__________,AC=__________.
9、已知A,B,O三点不在同一直线上,A,A′关于O点对称.B,B′关于O点对称,那么线段AB与A′B′__________.(填数量和位置关系)
10、如图,在矩形ABCD中,AB=3,BC=4,EF过AC、BD的交点O,则图中阴影部分的面积为__________.
11、如图,AB⊥BC,AB=BC=2cm,弧OA与弧OC关于点O中心对称,则AB、BC、弧CO、弧OA所围成的面积是__________cm2.
12、若△ABC与△DEF关于点O成中心对称,且A、B、C的对称点分别为D、E、F,若AB=5,AC=3,则EF的范围是__________.
13、如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为__________.
14、已知A、B、O三点不共线,如果点C与点A关于点O对称,点D与点B关于点O对称,那么线段AB与CD的关系是__________.
15、若线段AB、CD关于点P成中心对称,则线段AB、CD的关系是__________.
16、若矩形的对称中心到两边的距离差为4cm,周长为56cm,则矩形的边长分别为__________.
17、中央电视台大风车栏目图标如图甲,其中心为O,半圆固定,其半径为2r,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆内的轮片面积是不变的(如图乙),这个不变的面积值是
__________
.
18、如图,AB⊥BC,AB=BC=2cm,与关于点O中心对称,则AB、BC、、所围成的图形的面积是__________cm2.
19、如图,过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的__________.
20、如图△ABC与△DEF关于O点成中心对称.则线段BC与EF的关系是__________.
21、如图,线段AB关于点O(不在AB上)的对称线段是A′B′;线段A′B′关于点O′(不在A′B′上)的对称线段是A″B″.那么线段AB与线段A″B″的关系是__________.
三、解答题
22、在平面直角坐标系中,抛物线y=x2+5x+4的顶点为M,与x轴交于A,B两点,与y轴交于C点.
(1)求点A,B,C的坐标;
(2)求抛物线y=x2+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为M′,与x轴交于A′,B′两点,与y轴交于C′点,在以A,B,C,M,A′,B′,C′,M′这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积.
23、如图,在公园里有一块平行四边形的草坪,草坪里有一个圆形花坛,有关部门计划在草坪上修一条小路,这条小路要把草坪和花坛的面积同时平分,请在图中画出这条小路.(小路用AB表示)
24、如图,在四边形ABCD中,AD∥BC,E是CD的中点.
(1)画图:连接AF并延长,交BC的延长线于点F,连接BE;
(2)填空:点A与点F关于点__________成中心对称,若AB=AD+BC,则△ABF是__________三角形,此时点A与点F关于直线__________成轴对称;
(3)图中△__________的面积等于四边形ABCD的面积.
25、如图所示,已知梯形ABCD中,AD∥BC,请你利用中心对称的性质,把梯形ABCD转化成与原梯形面积相等的三角形,并简要说明变换理由.
26、已知:如图所示,E是等腰梯形一腰CD的中点,EF⊥AB,垂足为F,求证:S梯形ABCD=AB?EF.
27、轴对称图形的对称轴将图形面积二等分,中心对称图形过对称中心的直线将图形面积二等分.请用学过的知识将下图所示的图形面积分成相等的两部分.
试卷
第7/16页
利用中心对称的性质解决几何问题的答案和解析
一、选择题
1、答案:
A
试题分析:根据已知对各个结论进行分析从而确定最后的答案.
①正确,根据等底等高可证明S△ADE=S△EOD;
②正确,根据已知及菱形的性质可证明△DEF≌△BEF;
③正确,可证明得△DEO≌△DFO;
④错误,每一条对角线平分一组对角,可得∠ADO=∠CDO,∠EDO=∠FDO,所以∠ADE=∠CDF≠∠EDO;
故选A.
2、答案:
C
试题分析:根据矩形对角线相等且平分的性质,易证△OEC≌△OFA,△DEO≌△BFO,△AOD≌△BOC,即可证明.
试题解析:∵四边形ABCD是矩形,
∴AD=BC,AO=BO=CO=DO,
∴△AOD≌△BOC,
∵∠ECO=∠FAO,OA=OC,∠EOC=∠FOA,
∴△OEC≌△OFA,
同理可证,△DEO≌△BFO,
∴S1=S2.
故选:C.
3、答案:
D
试题分析:根据中心对称图形的性质,即可作出判断.
试题解析:A、根据中心对称的两个图形全等,即可得到,故正确;
B、中心对称图形中,对称点到对称中心的距离相等,故正确;
C、根对称点到对称中心的距离相等,即可证得对应线段平行,故正确;
D、不正确.
故选D.
4、答案:
C
试题分析:由平行四边形的性质易得:△AON≌△COM(AAS),△AOE≌△COF,△BOE≌△DOF,△BOG≌△DOH,继而可证得△GOM≌△HON(SAS),则可得S阴影=S?ABCD.
试题解析:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,AB∥CD,
∴∠OAN=∠OCM,
在△AON和△COM中,
,
∴△AON≌△COM(AAS),
同理:△AOE≌△COF,△BOE≌△DOF,△BOG≌△DOH,
∴OG=OH,OM=ON,
在△GOM和△HON中,
,
∴△GOM≌△HON(SAS),
∴S阴影=S?ABCD=×6×4=12.
故选C.
5、答案:
D
试题分析:根据中心对称的定义和中心对称的性质作答.
试题解析:A、∵AD与EF关于点O成中心对称,∴AD∥EF,同理可得AB∥GF,所以说法正确;
B、∵B与G关于点O成中心对称,∴BO=GO,所以说法正确;
C、∵CD与HE关于点O成中心对称,∴CD=HE,同理可得BC=GH,所以说法正确;
D、∵D与E关于点O成中心对称,∴DO=EO,所以DO=HO错误.
故选D.
二、填空题
6、答案:
试题分析:根据中心对称的性质、菱形和平行四边形是中心对称图形矩形解答即可.
试题解析:如图,连接BF、AE交于M,连接BD、EC交于N,
作直线MN,则直线MN即为所求.
7、答案:
试题分析:连接AB,则阴影部分面积=2(S扇形AOB-S△ABO),依此计算即可求解.
试题解析:
由题意得,阴影部分面积=2(S扇形AOB-S△AOB)=2(-×2×2)=2π-4.
故答案为:2π-4.
8、答案:
试题分析:利用关于某点对称的图形全等,这样可以得出対应边与对应角之间的关系,进而解决.
试题解析:∵△ABC与△DEF关于O点成中心对称
∴△ABC≌△DEF
AB=DE,AC=DF
又∵BO=OE,CO=OF,∠BOC=∠FOE
∴△BOC≌△EOF
∴∠BCO=∠OFE
BC∥EF
故填:=,EF,DF
9、答案:
试题分析:根据中心对称图形对应线段平行且相等的性质填空.
试题解析:中心对称图形中的不在同一直线上的两条对应线段的关系是:平行且相等.
故答案为:平行且相等.
10、答案:
试题分析:易证△AOE≌△COF,则阴影部分的面积为△CDO的面积,根据矩形对角线分成的四部分面积相等,即可计算阴影部分的面积,即可解题.
试题解析:∵AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
则△AOE和△COF面积相等,
∴阴影部分的面积与△CDO的面积相等,
又∵矩形对角线将矩形分成面积相等的四部分,
∴阴影部分的面积为:×3×4=3.
故答案为:3.
11、答案:
试题分析:由弧OA与弧OC关于点O中心对称,根据中心对称的定义,如果连接AC,则点O为AC的中点,则题中所求面积等于△BAC的面积.
连接AC.
∵弧OA与弧OC关于点O中心对称,
∴点O为AC的中点,
∴AB、BC、弧CO、弧OA所围成的面积=△BAC的面积==2cm2.
12、答案:
试题分析:根据成中心对称的两个图形对应线段长相等可知EF的取值范围等于BC的取值范围;
试题解析:∵△ABC与△DEF关于点O成中心对称,且A、B、C的对称点分别为D、E、F,AB=5,AC=3,
∴DE=5,DF=3
∴EF的取值范围为:2<EF<8
故答案为:2<EF<8
13、答案:
试题分析:根据矩形是中心对称图形寻找思路:△OBF≌△ODE,图中阴影部分的面积就是△ADC的面积.
试题解析:根据矩形的性质得△OBF≌△ODE,
属于图中阴影部分的面积就是△ADC的面积.
S△ADC=CD×AD=×2×3=3.
故答案为:3.
14、答案:
试题分析:根据关于点对称的性质得出AO=BO,DO=BO,进而得出四边形ABCD是平行四边形,即可得出答案.
试题解析:∵AO=BO,DO=BO,
∴四边形ABCD是平行四边形,
∴ABCD,
故答案为:ABCD.
15、答案:
试题分析:根据线段AB、CD关于点P成中心对称,再根据中心对称的性质得出对应边之间的关系即可.
试题解析:∵线段AB、CD关于点P成中心对称,
∴线段AB、CD的关系是:平行且相等.
故答案为:平行且相等.
16、答案:
试题分析:如图,设FO=y,EO=x,可以得出2x=AD,2y=AB.可列出两个等式解答即可.
试题解析:设FO=y,EO=x.
故2x=AD,2y=AB.
2×(2x+2y)=56
x-y=4
可得x=5,y=9
所以这个矩形的两邻边长分别为10cm和18cm.
故答案为:10cm,18cm.
17、答案:
试题分析:四个阴影部分的图形正好构成一个中心对称图形,AB过对称中心,根据其中心对称图形的性质,则这个不变的面积是半圆面积的一半,即可求解.
试题解析:这个不变的面积是半圆面积的一半,即××4r2=πr2.
18、答案:
试题分析:连AC,则△ABC为等腰直角三角形,由与关于点O中心对称得到OA=OC,弧OA=弧OC,则弓形OA的面积=弓形OC的面积,因此AB、BC、、所围成的图形的面积=三角形ABC的面积,然后根据直角三角形的面积公式计算即可.
连AC,如图,
∵AB⊥BC,AB=BC=2cm,
∴△ABC为等腰直角三角形,
又∵与关于点O中心对称,
∴OA=OC,弧OA=弧OC,
∴弓形OA的面积=弓形OC的面积,
∴AB、BC、、所围成的图形的面积=三角形ABC的面积=×2×2=2(cm2).
故答案为2.
19、答案:
试题分析:根据矩形的性质,将面积转换后求解即可.
由图可知:OB=OD,∠OBE=∠ODF,∠EOB=∠FOD,
∴△BEO≌△DFO,
∴S△DFO=S△BEO,
∵在△ABO与△AOD中,OB=OD,高相等,
∴S△ABO=S△AOD,
即S△ABO=S△ABD=S?ABCD,
阴影部分的面积=S△AEO+S△DFO=S△AEO+S△BEO=S△ABO=S?ABCD.
故答案为:.
20、答案:
试题分析:根据△ABC与△DEF关于O点成中心对称,得出对应边之间的关系即可得出答案.
试题解析:∵△ABC与△DEF关于O点成中心对称.
∴线段BC与EF的关系是:平行且相等.
故答案为:平行且相等.
21、答案:
试题分析:根据中心对称的概念可知线段AB、A′B′、上的对应点都关于点O对称,A'B'、A''B''上的对应点都关于O'对称.
试题解析:中心对称图形中的不在同一直线上的两条对应线段的关系是:平行且相等.
故线段AB与线段A″B″的关系是:平行且相等.
故答案为:平行且相等.
三、解答题
22、答案:
试题分析:(1)令y=0,求出x的值;令x=0,求出y,即可解答;
(2)先求出A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,-4),再代入解析式,即可解答;
(3)取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,由此判定四边形AMA′M′为平行四边形,又知AA′与MM′不垂直,从而平行四边形AMA′M′不是菱形,过点M作MD⊥x轴于点D,求出抛物线的顶点坐标M,根据,即可解答.
试题解析:(1)令y=0,得x2+5x+4=0,
∴x1=-4,x2=-1,
令x=0,得y=4,
∴A(-4,0),B(-1,0),C(0,4).
(2)∵A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,-4),
∴所求抛物线的函数表达式为y=ax2+bx-4,
将(4,0),(1,0)代入上式,得
解得:,
∴y=-x2+5x-4.
(3)如图,取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,
由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,
∴四边形AMA′M′为平行四边形,
又知AA′与MM′不垂直,
∴平行四边形AMA′M′不是菱形,
过点M作MD⊥x轴于点D,
∵y=,
∴M(),
又∵A(-4,0),A′(4,0)
∴AA′=8,MD=,
∴=
23、答案:
试题分析:利用平行四边形的性质以及圆的性质,得出对角线交点与圆心连线即可平分面积.
试题解析:如图所示:线段AB即为所求.
24、答案:
试题分析:(1)根据要求直接作出图形即可;
(2)利用中心对称的定义回答即可,然后证得AB=BF,利用等腰三角形的性质判定等腰三角形即可;
(3)得到三角形ADE的面积等于三角形ECF的面积,从而得到答案;
试题解析:(1)如图:
(2)∵AD∥BC,
∴∠D=∠DCF,
∵DE=CE,∠AED=∠FEC
在△ADE与△FCE中,
∴△ADE≌△FCE(ASA),
∴AE=FE,AD=CF,
∴点A与点F关于点E成中心对称,
∵若AB=AD+BC,
∴AB=BF,
则△ABF是等腰三角形,此时点A与点F关于直线BE成轴对称;
(3)图中△ABFD?面积等于四边形ABCD的面积.
故答案为:E,等腰,BE,ABF.
25、答案:
试题分析:根据中心对称图形的性质以及全等三角形的判定与性质得出即可.
解;取CD中点M,连接AM并延长交BC延长线于点N,得到△ABN即为与原梯形面积相等的三角形.
在△ADM和△NCM中
,
∴△ADM≌△NCM(ASA),
△NCM可以看作是△ADM关于点M的中心对称图形,
∴△ABN即为与原梯形面积相等的三角形.
26、答案:
试题分析:连接AE交BC的延长线于G点,则梯形ABCD的面积就是△ABE的面积的2倍,则问题就可以比较容易求解.
试题解析:证明:如图,连接AE交BC的延长线于G点,连接BE,
∵AD∥CG,
∴∠D=∠ECG,
在△ADE和△GCE中
∴△ADE≌△GCE(ASA),
∴AE=GE,
∴可得:S△ABG=S梯形ABCD=2S△ABE=AB×FE.
27、答案:
试题分析:利用轴对称图形的对称轴将图形面积二等分,中心对称图形过对称中心的直线将图形面积二等分.分别得出图形的对称轴与对称中心即可得出答案.
试题解析:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
