切线长定理
图片预览



文档简介
(共25张PPT)
切 线 长 定 理
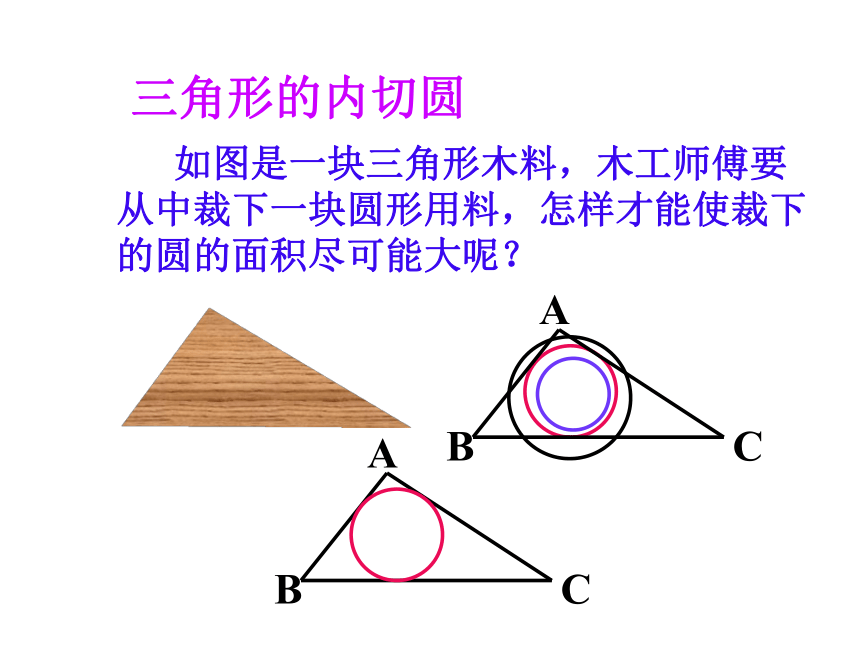
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
P
B
C
O
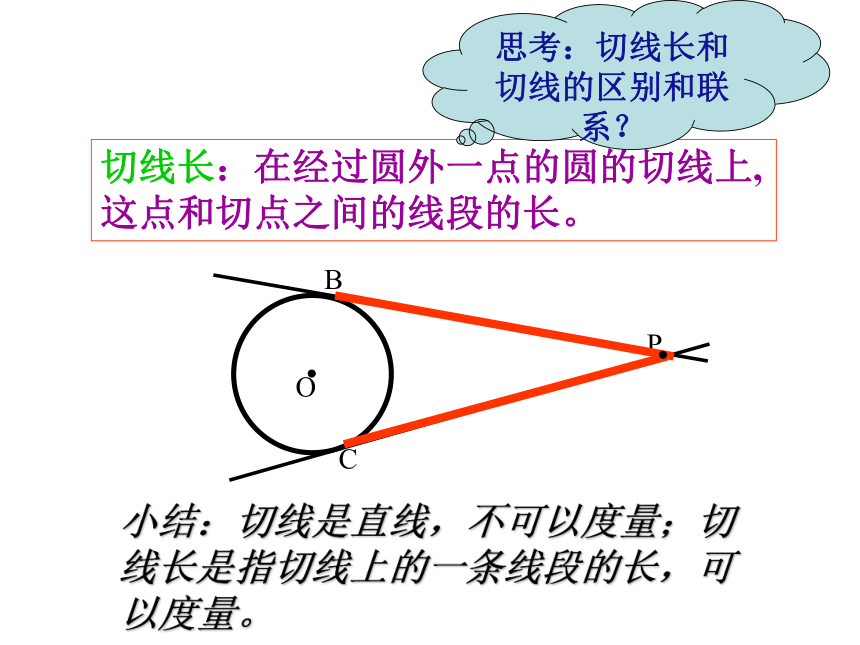
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。
思考:切线长和切线的区别和联系?
小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
p
A
B
O
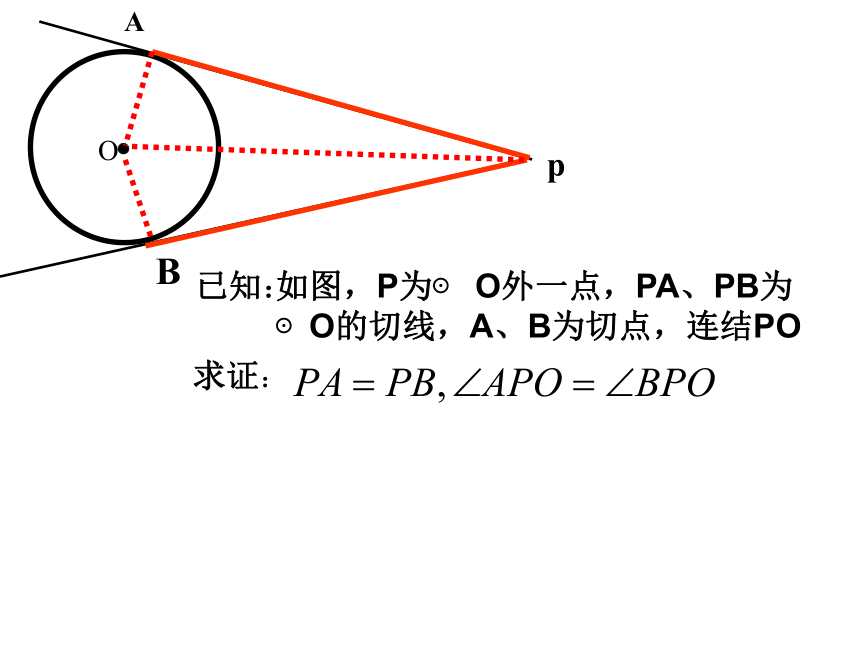
已知:
求证:
如图,P为⊙ O外一点,PA、PB为
⊙O的切线,A、B为切点,连结PO
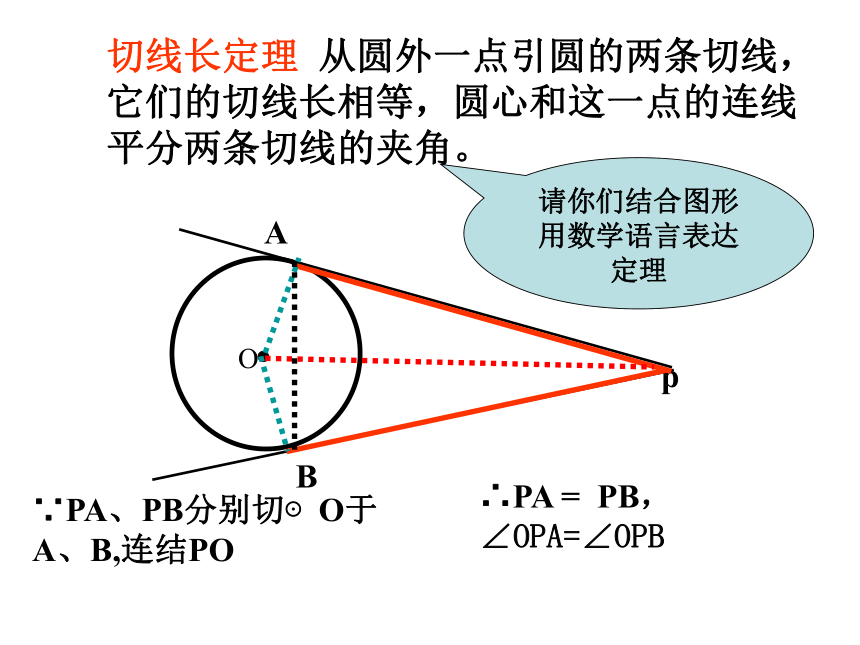
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
p
A
B
O
请你们结合图形用数学语言表达定理
∵PA、PB分别切⊙O于A、B,连结PO
∴PA = PB,∠OPA=∠OPB
A
B
C
M
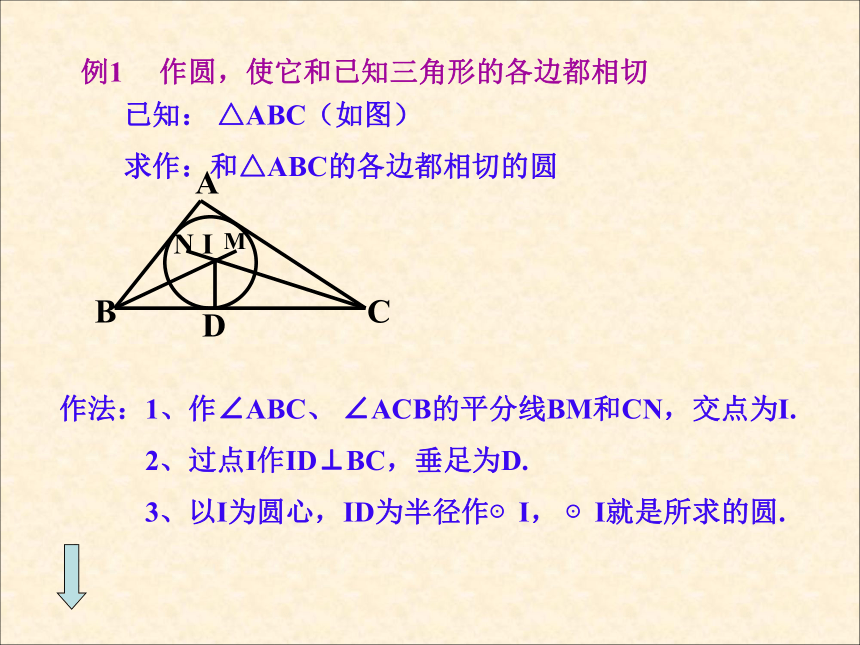
例1 作圆,使它和已知三角形的各边都相切
已知: △ABC(如图)
求作:和△ABC的各边都相切的圆
作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.
N
I
D
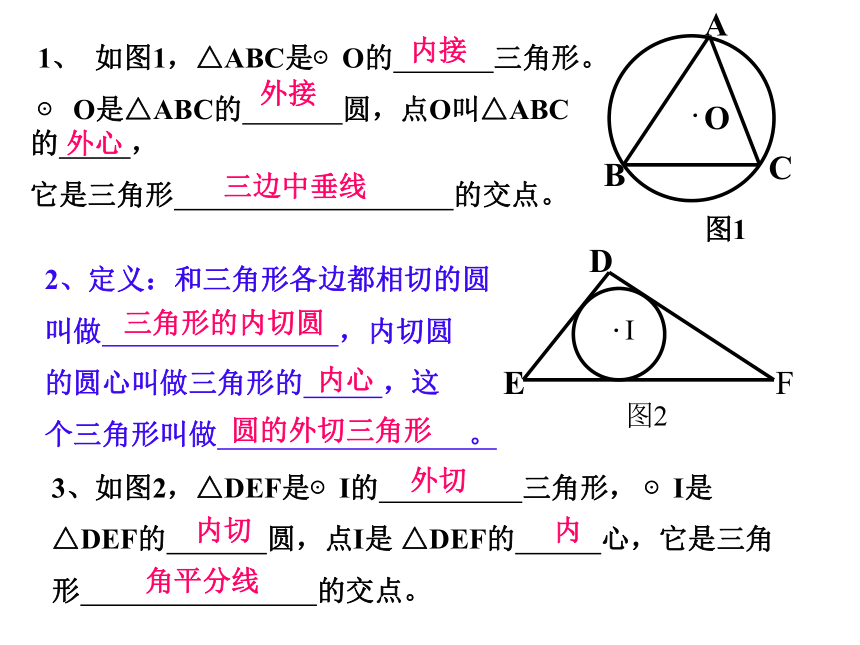
1、 如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,点O叫△ABC的 ,
它是三角形 的交点。
外接
内接
外心
三边中垂线
3、如图2,△DEF是⊙I的 三角形, ⊙I是
△DEF的 圆,点I是 △DEF的 心,它是三角
形 的交点。
2、定义:和三角形各边都相切的圆
叫做 ,内切圆
的圆心叫做三角形的 ,这
个三角形叫做 。
A
B
C
O
.
图1
I
D
E
F
.
图2
三角形的内切圆
内心
圆的外切三角形
外切
内切
内
角平分线
三角形内心的性质:
1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的角平分线上;
1、三角形的外心到三角形各个顶点的距离相等;
2、三角形的外心在三角形三边的垂直平分线上;
三角形外心的性质:
C
A
B
.
I
D
E
F
.
O
定义:和多边形各边都相切的圆
叫做 ,这个
多边形叫做 。
多边形的内切 圆
圆的外切多边形
内切
外切
如上图,四边形DEFG是⊙O的 四边形,
⊙O是四边形DEFG的 圆,
D
E
F
G
.O
例1 如图,在△ABC中,点O是内心, (1)若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
A
B
C
O
(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
解(1)∵点O是△ABC的内心,
∴ ∠OBC= ∠OBA= ∠ABC= 25 °
同理 ∠OCB= ∠OCA= ∠ACB=35 °
∴ ∠BOC=180 °- (∠OBC+ ∠OCB) = 180 °-60 °=120 °
130
20
(4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
理由: ∵点O是△ABC的内心,
∴ ∠OBC= ∠ABC, ∠OCB= ∠ACB
∴ ∠OBC+ ∠OCB = (∠ABC+ ∠ACB)
= (180 ° - ∠A )= 90 ° - ∠A
在△ABC中, ∠BOC =180 °-( ∠OBC+ ∠OCB )
= 180 °-( 90 ° - ∠A )= 90 °+ ∠A
A
B
C
O
答: ∠BOC =90 ° + ∠A
例2、如图,设△ABC的周长为c,内切
⊙o和各边分别相切于D,E,F
求证:AE+BC= C
C
B
A
E
D
F
O
r
I
C
A
B
E
D
F
如图,在Rt△ABC中,斜边AB=10,AC=8,⊙I分别切三边于点D、E、F,
试求BF长及⊙I的半径。
O
P
A
B
C
D
E
如图,⊙O分别切∠APB两边于A、B, CD切⊙O于E,交PA、PB于C、D,
1)如果PA=8,则△PCD的周长为______
2) 如果∠P=50°则∠COD=_____
C
P
O
B
I
A
O
D
A
C
B
E
如图,在Rt△ABC中,斜边AB=10,AC=6,D是BC上一点,以CD为直径的半圆O切AB于点E,求CD的长
O
A
B
C
E
D
F
G
如图,在Rt△ABC中,D、E是斜边AB上两点,以DE为直径的半圆O切AC、BC于点F、G,
1)AB=10, AC=6,求DE的长;
2)AF=1,GB=2,求DE的长
I
A
B
C
D
E
F
G
H
如图在梯形ABCD中,AD∥BC, ⊙I是梯形的内切圆,切点分别为E、F、G、H
1)求证:AD+BC=AB+CD
2)如果AB=CD,AD=1,BC=3,试求梯形的面积
小结
1、切线长定理
2、内切圆、内心
3、面积方法S= Cr
名称 确定
方法 图形 性质
外心
内心
三角形三边中垂线的交点
三角形三条角平分线的交点
(三角形外接圆的圆心)
(三角形内切圆的圆心)
1.OA=OB=OC;2.外心不一定在三角形的内部.
1.到三边的距离相等;2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
3.内心在三角形内部.
D
O
P
A
B
C
再 见
(1)作圆的关键是什么
提出以下几个问题进行讨论:
(2)假设⊙I是所求作的圆,⊙I和三
角形三边都相切,圆心I应满足什么
条件
(3)这样的点I应在什么位置
(4)圆心I确定后半径如何找?
结论:和三角形的各边都相切的圆可以作一个且只可以作出一个.
A
B
C
I
M
N
D
A
B
C
切 线 长 定 理
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
P
B
C
O
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。
思考:切线长和切线的区别和联系?
小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
p
A
B
O
已知:
求证:
如图,P为⊙ O外一点,PA、PB为
⊙O的切线,A、B为切点,连结PO
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
p
A
B
O
请你们结合图形用数学语言表达定理
∵PA、PB分别切⊙O于A、B,连结PO
∴PA = PB,∠OPA=∠OPB
A
B
C
M
例1 作圆,使它和已知三角形的各边都相切
已知: △ABC(如图)
求作:和△ABC的各边都相切的圆
作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.
N
I
D
1、 如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,点O叫△ABC的 ,
它是三角形 的交点。
外接
内接
外心
三边中垂线
3、如图2,△DEF是⊙I的 三角形, ⊙I是
△DEF的 圆,点I是 △DEF的 心,它是三角
形 的交点。
2、定义:和三角形各边都相切的圆
叫做 ,内切圆
的圆心叫做三角形的 ,这
个三角形叫做 。
A
B
C
O
.
图1
I
D
E
F
.
图2
三角形的内切圆
内心
圆的外切三角形
外切
内切
内
角平分线
三角形内心的性质:
1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的角平分线上;
1、三角形的外心到三角形各个顶点的距离相等;
2、三角形的外心在三角形三边的垂直平分线上;
三角形外心的性质:
C
A
B
.
I
D
E
F
.
O
定义:和多边形各边都相切的圆
叫做 ,这个
多边形叫做 。
多边形的内切 圆
圆的外切多边形
内切
外切
如上图,四边形DEFG是⊙O的 四边形,
⊙O是四边形DEFG的 圆,
D
E
F
G
.O
例1 如图,在△ABC中,点O是内心, (1)若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
A
B
C
O
(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
解(1)∵点O是△ABC的内心,
∴ ∠OBC= ∠OBA= ∠ABC= 25 °
同理 ∠OCB= ∠OCA= ∠ACB=35 °
∴ ∠BOC=180 °- (∠OBC+ ∠OCB) = 180 °-60 °=120 °
130
20
(4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
理由: ∵点O是△ABC的内心,
∴ ∠OBC= ∠ABC, ∠OCB= ∠ACB
∴ ∠OBC+ ∠OCB = (∠ABC+ ∠ACB)
= (180 ° - ∠A )= 90 ° - ∠A
在△ABC中, ∠BOC =180 °-( ∠OBC+ ∠OCB )
= 180 °-( 90 ° - ∠A )= 90 °+ ∠A
A
B
C
O
答: ∠BOC =90 ° + ∠A
例2、如图,设△ABC的周长为c,内切
⊙o和各边分别相切于D,E,F
求证:AE+BC= C
C
B
A
E
D
F
O
r
I
C
A
B
E
D
F
如图,在Rt△ABC中,斜边AB=10,AC=8,⊙I分别切三边于点D、E、F,
试求BF长及⊙I的半径。
O
P
A
B
C
D
E
如图,⊙O分别切∠APB两边于A、B, CD切⊙O于E,交PA、PB于C、D,
1)如果PA=8,则△PCD的周长为______
2) 如果∠P=50°则∠COD=_____
C
P
O
B
I
A
O
D
A
C
B
E
如图,在Rt△ABC中,斜边AB=10,AC=6,D是BC上一点,以CD为直径的半圆O切AB于点E,求CD的长
O
A
B
C
E
D
F
G
如图,在Rt△ABC中,D、E是斜边AB上两点,以DE为直径的半圆O切AC、BC于点F、G,
1)AB=10, AC=6,求DE的长;
2)AF=1,GB=2,求DE的长
I
A
B
C
D
E
F
G
H
如图在梯形ABCD中,AD∥BC, ⊙I是梯形的内切圆,切点分别为E、F、G、H
1)求证:AD+BC=AB+CD
2)如果AB=CD,AD=1,BC=3,试求梯形的面积
小结
1、切线长定理
2、内切圆、内心
3、面积方法S= Cr
名称 确定
方法 图形 性质
外心
内心
三角形三边中垂线的交点
三角形三条角平分线的交点
(三角形外接圆的圆心)
(三角形内切圆的圆心)
1.OA=OB=OC;2.外心不一定在三角形的内部.
1.到三边的距离相等;2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
3.内心在三角形内部.
D
O
P
A
B
C
再 见
(1)作圆的关键是什么
提出以下几个问题进行讨论:
(2)假设⊙I是所求作的圆,⊙I和三
角形三边都相切,圆心I应满足什么
条件
(3)这样的点I应在什么位置
(4)圆心I确定后半径如何找?
结论:和三角形的各边都相切的圆可以作一个且只可以作出一个.
A
B
C
I
M
N
D
A
B
C
同课章节目录
