人教版八年级数学下册同步练习_19.2《一次函数》(word含答案)
文档属性
| 名称 | 人教版八年级数学下册同步练习_19.2《一次函数》(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 21:49:50 | ||
图片预览

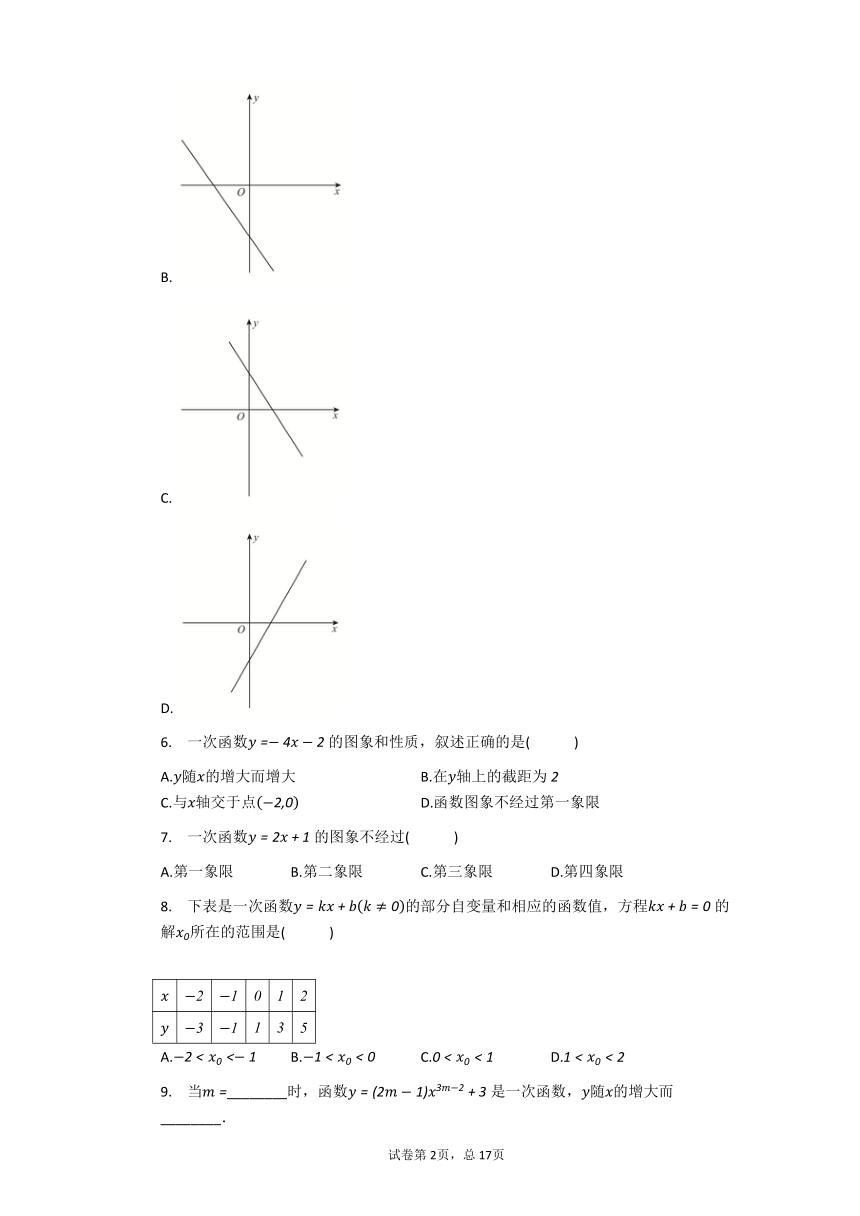



文档简介
人教版八年级数学下册同步练习
19.2《一次函数》
?
1.
已知是正比例函数,则的值是(?
?
?
?
)
A.
B.
C.
D.
2.
下列问题中,成正比例关系的有(
)
A.人的身高与体重
B.正三角形的面积与它的边长
C.买同一种练习本所需的钱数和所买的本数
D.从甲地到乙地,所用的时间与行驶的速度?
3.
若,则下列函数①,②,③,的值随的值的增大而增大的函数有(
)
A.个
B.个
C.个
D.个?
4.
下列函数①;②;③;④;⑤,其中表示一次函数的有(?
?
?
?
)
A.个
B.个
C.个
D.个
5.
已知一次函数
的函数值随的增大而增大,则该函数的图象大致是()
A.
B.
C.
D.?
6.
一次函数的图象和性质,叙述正确的是(?
?
?
?
)
A.随的增大而增大
B.在轴上的截距为
C.与轴交于点
D.函数图象不经过第一象限?
7.
一次函数的图象不经过(?
?
?
?
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.
下表是一次函数的部分自变量和相应的函数值,方程的解所在的范围是(?
?
?
?
)
A.
B.
C.
D.?
9.
当________时,函数是一次函数,随的增大而________.
?
10.
平面直角坐标系中,若一次函数图象与直线交于点,且与直线无交点,则该一次函数的解析式为________.
?
11.
如图,一次函数和交于点,则的解集为________.
?
12.
已知一次函数的图象经过原点,则________.
13.
已知=
(1)当,取何值时,是的一次函数?
(2)当,取何值时,是的正比例函数?
?
14.
若与成正比,且=时,=,求关于的函数表达式.
?
15.
已知正比例函数.求:
(1)为何值时,函数图象经过一、三象限;
(2)为何值时,随的增大而减小;
(3)为何值时,点在该函数图象上.
?
16.
已知一次函数的图象与的图象平行,并且该函数图象经过点.求该函数的解析式.
?
17.
某经销商从市场得知如下信息:
某品牌空调扇
某品牌电风扇
进价(元台)
售价(元台)
他计划用不超过万元资金一次性购进该品牌空调扇和电风扇共台,设该经销商购进空调扇台,空调扇和电风扇全部销售完后获得利润为元.
写出与之间的函数关系式,并求出自变量的取值范围;
该经销商如何进货获利最大?并求出最大利润.
?
18.
在平面直角坐标系中,已知点的坐标为,点的坐标为.
求直线的表达式;
若点的坐标为,且,求的值;
若点的坐标为,在射线上有两点,,使得以,,为顶点的三角形与全等,求点的坐标.
参考答案
人教版八年级数学下册同步练习
19.2《一次函数》
一、
选择题
1.
【答案】
D
【解答】
解:∵
是正比例函数,
∴
且,
解得.
故选.
2.
【答案】
C
【解答】
解:根据正比例函数的定义,成正比例关系的是买同一种练习本所需的钱数和所买的本数.
故选.
3.
【答案】
C
【解答】
解:①当时,反比例函数的图象在第四象限内随的增大而增大,故正确;
②当时,,则一次函数的图象是随的增大而增大,故正确;
③当当时,正比例函数的图象是随的增大而减小,故错误;
综上所述,正确的结论有个.
故选:.
4.
【答案】
B
【解答】
解:一般地,形如(,、是常数)的函数,叫做一次函数.
,是一次函数;
,不是一次函数;
,是一次函数;
,不是一次函数;
是一次函数.
故选.
5.
【答案】
A
【解答】
解:∵
一次函数的函数值随的增大而增大,
∴
,可排除选项和,
令,则,
故该一次函数与轴的交点坐标为,可排除选项.
故选.
6.
【答案】
D
【解答】
解:,由可知,随的增大而减小,
故选项错误;
,令,得,
则在轴上的截距为,故选项错误;
,令,得,
则与轴交于点,故选项错误;
,,,
根据一次函数的性质可知,函数图象不经过第一象限,
故选项正确.
故选.
7.
【答案】
D
【解答】
解:根据一次函数的系数判断出函数图象所经过的象限,由,可知,
一次函数的图象过一、二、三象限,不经过第四象限.
故选.
8.
【答案】
B
【解答】
解:由一次函数的表格可知,随的增大而增大,
且,,
,,
∴
时,一定存在,使得,
即方程的解所在的范围是.
故选.
二、
填空题
【答案】
,增大
【解答】
解:①是一次函数,
所以,;
②当时,,故,,随的增大而增大.
10.
【答案】
【解答】
解:∵
点在上,
∴
,
解得,
∴
.
设一次函数的解析式为,
由题意,得,
解得,
∴
该一次函数的解析式为.
故答案为:.
11.
【答案】
【解答】
解:由题设,
即,
由图象得,当时,.
故答案为:.
12.
【答案】
【解答】
解:由题意可得:
解得:,
故答案为:
三、
解答题
13.
【答案】
(1)当,取任意数时,是的一次函数
(2)当时,是的正比例函数.
【解答】
(1)由题意得
所以
所以当,取任意数时,是的一次函数.
(2)由题意得
所以
所以当时,是的正比例函数.
14.
【答案】
【解答】
此题暂无解答
15.
【答案】
解:(1)∵
函数图象经过一、三象,
∴
,解得;
(2)∵
随的增大而减小,
∴
,解得;
(3)∵
点在该函数图象上,
∴
,解得.
【解答】
解:(1)∵
函数图象经过一、三象,
∴
,解得;
(2)∵
随的增大而减小,
∴
,解得;
(3)∵
点在该函数图象上,
∴
,解得.
16.
【答案】
解:∵
一次函数的图象与的图象平行,
∴
,
将代入,得,
则该函数解析式为.
【解答】
解:∵
一次函数的图象与的图象平行,
∴
,
将代入,得,
则该函数解析式为.
17.
【答案】
解:设该经销商购进空调扇台,则购进电风扇台,
?
,
由,
解得,
∴
自变量的取值范围是.
∵
,,
∴
随的增大而增大,
∴
当时,有最大值,最大值(元),
此时,(台),
∴
该经销商分别购进空调扇和电风扇各台时,获利最大,最大利润为元.
【解答】
解:设该经销商购进空调扇台,则购进电风扇台,
?
,
由,
解得,
∴
自变量的取值范围是.
∵
,,
∴
随的增大而增大,
∴
当时,有最大值,最大值(元),
此时,(台),
∴
该经销商分别购进空调扇和电风扇各台时,获利最大,最大利润为元.
18.
【答案】
解:∵
点在直线上,
故可设直线的表达式为.
又∵
点在直线上,
∴
,
∴
,
∴
直线的表达为?.?
过作轴交于,
∵
点的坐标为,
∴
点的纵坐标为.
当时,,
解得,
∴
,
∴
,
∴
.
∵
,
∴
,
解得或?.?
①当点在线段上时,
若点在,之间,
当,且时,
.
∵
,,
∴
.
设中边上的高为,
则,
∴
,
∴
,
∴
,
∴
点的横坐标为.
当时,,
∴
?
.?
若点在,之间,
当,且时有,
则,
∴
,
∴
.
作于,
则,
∴
,
∴
.
当时,?,
解得,
∴
.
②当点在的延长线上时,
若点在,之间,且,时,,
作于,于,
则,
∴
点的纵坐标为,
当时,,
解得,
∴
.
若点在的延长线上或的反向延长线上,都不存在满足条件的,两点.
综上所述,满足条件的点为,,.
【解答】
解:∵
点在直线上,
故可设直线的表达式为.
又∵
点在直线上,
∴
,
∴
,
∴
直线的表达为?.?
过作轴交于,
∵
点的坐标为,
∴
点的纵坐标为.
当时,,
解得,
∴
,
∴
,
∴
.
∵
,
∴
,
解得或?.?
①当点在线段上时,
若点在,之间,
当,且时,
.
∵
,,
∴
.
设中边上的高为,
则,
∴
,
∴
,
∴
,
∴
点的横坐标为.
当时,,
∴
?
.?
若点在,之间,
当,且时有,
则,
∴
,
∴
.
作于,
则,
∴
,
∴
.
当时,?,
解得,
∴
.
②当点在的延长线上时,
若点在,之间,且,时,,
作于,于,
则,
∴
点的纵坐标为,
当时,,
解得,
∴
.
若点在的延长线上或的反向延长线上,都不存在满足条件的,两点.
综上所述,满足条件的点为,,.
试卷第4页,总9页
试卷第5页,总9页
19.2《一次函数》
?
1.
已知是正比例函数,则的值是(?
?
?
?
)
A.
B.
C.
D.
2.
下列问题中,成正比例关系的有(
)
A.人的身高与体重
B.正三角形的面积与它的边长
C.买同一种练习本所需的钱数和所买的本数
D.从甲地到乙地,所用的时间与行驶的速度?
3.
若,则下列函数①,②,③,的值随的值的增大而增大的函数有(
)
A.个
B.个
C.个
D.个?
4.
下列函数①;②;③;④;⑤,其中表示一次函数的有(?
?
?
?
)
A.个
B.个
C.个
D.个
5.
已知一次函数
的函数值随的增大而增大,则该函数的图象大致是()
A.
B.
C.
D.?
6.
一次函数的图象和性质,叙述正确的是(?
?
?
?
)
A.随的增大而增大
B.在轴上的截距为
C.与轴交于点
D.函数图象不经过第一象限?
7.
一次函数的图象不经过(?
?
?
?
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.
下表是一次函数的部分自变量和相应的函数值,方程的解所在的范围是(?
?
?
?
)
A.
B.
C.
D.?
9.
当________时,函数是一次函数,随的增大而________.
?
10.
平面直角坐标系中,若一次函数图象与直线交于点,且与直线无交点,则该一次函数的解析式为________.
?
11.
如图,一次函数和交于点,则的解集为________.
?
12.
已知一次函数的图象经过原点,则________.
13.
已知=
(1)当,取何值时,是的一次函数?
(2)当,取何值时,是的正比例函数?
?
14.
若与成正比,且=时,=,求关于的函数表达式.
?
15.
已知正比例函数.求:
(1)为何值时,函数图象经过一、三象限;
(2)为何值时,随的增大而减小;
(3)为何值时,点在该函数图象上.
?
16.
已知一次函数的图象与的图象平行,并且该函数图象经过点.求该函数的解析式.
?
17.
某经销商从市场得知如下信息:
某品牌空调扇
某品牌电风扇
进价(元台)
售价(元台)
他计划用不超过万元资金一次性购进该品牌空调扇和电风扇共台,设该经销商购进空调扇台,空调扇和电风扇全部销售完后获得利润为元.
写出与之间的函数关系式,并求出自变量的取值范围;
该经销商如何进货获利最大?并求出最大利润.
?
18.
在平面直角坐标系中,已知点的坐标为,点的坐标为.
求直线的表达式;
若点的坐标为,且,求的值;
若点的坐标为,在射线上有两点,,使得以,,为顶点的三角形与全等,求点的坐标.
参考答案
人教版八年级数学下册同步练习
19.2《一次函数》
一、
选择题
1.
【答案】
D
【解答】
解:∵
是正比例函数,
∴
且,
解得.
故选.
2.
【答案】
C
【解答】
解:根据正比例函数的定义,成正比例关系的是买同一种练习本所需的钱数和所买的本数.
故选.
3.
【答案】
C
【解答】
解:①当时,反比例函数的图象在第四象限内随的增大而增大,故正确;
②当时,,则一次函数的图象是随的增大而增大,故正确;
③当当时,正比例函数的图象是随的增大而减小,故错误;
综上所述,正确的结论有个.
故选:.
4.
【答案】
B
【解答】
解:一般地,形如(,、是常数)的函数,叫做一次函数.
,是一次函数;
,不是一次函数;
,是一次函数;
,不是一次函数;
是一次函数.
故选.
5.
【答案】
A
【解答】
解:∵
一次函数的函数值随的增大而增大,
∴
,可排除选项和,
令,则,
故该一次函数与轴的交点坐标为,可排除选项.
故选.
6.
【答案】
D
【解答】
解:,由可知,随的增大而减小,
故选项错误;
,令,得,
则在轴上的截距为,故选项错误;
,令,得,
则与轴交于点,故选项错误;
,,,
根据一次函数的性质可知,函数图象不经过第一象限,
故选项正确.
故选.
7.
【答案】
D
【解答】
解:根据一次函数的系数判断出函数图象所经过的象限,由,可知,
一次函数的图象过一、二、三象限,不经过第四象限.
故选.
8.
【答案】
B
【解答】
解:由一次函数的表格可知,随的增大而增大,
且,,
,,
∴
时,一定存在,使得,
即方程的解所在的范围是.
故选.
二、
填空题
【答案】
,增大
【解答】
解:①是一次函数,
所以,;
②当时,,故,,随的增大而增大.
10.
【答案】
【解答】
解:∵
点在上,
∴
,
解得,
∴
.
设一次函数的解析式为,
由题意,得,
解得,
∴
该一次函数的解析式为.
故答案为:.
11.
【答案】
【解答】
解:由题设,
即,
由图象得,当时,.
故答案为:.
12.
【答案】
【解答】
解:由题意可得:
解得:,
故答案为:
三、
解答题
13.
【答案】
(1)当,取任意数时,是的一次函数
(2)当时,是的正比例函数.
【解答】
(1)由题意得
所以
所以当,取任意数时,是的一次函数.
(2)由题意得
所以
所以当时,是的正比例函数.
14.
【答案】
【解答】
此题暂无解答
15.
【答案】
解:(1)∵
函数图象经过一、三象,
∴
,解得;
(2)∵
随的增大而减小,
∴
,解得;
(3)∵
点在该函数图象上,
∴
,解得.
【解答】
解:(1)∵
函数图象经过一、三象,
∴
,解得;
(2)∵
随的增大而减小,
∴
,解得;
(3)∵
点在该函数图象上,
∴
,解得.
16.
【答案】
解:∵
一次函数的图象与的图象平行,
∴
,
将代入,得,
则该函数解析式为.
【解答】
解:∵
一次函数的图象与的图象平行,
∴
,
将代入,得,
则该函数解析式为.
17.
【答案】
解:设该经销商购进空调扇台,则购进电风扇台,
?
,
由,
解得,
∴
自变量的取值范围是.
∵
,,
∴
随的增大而增大,
∴
当时,有最大值,最大值(元),
此时,(台),
∴
该经销商分别购进空调扇和电风扇各台时,获利最大,最大利润为元.
【解答】
解:设该经销商购进空调扇台,则购进电风扇台,
?
,
由,
解得,
∴
自变量的取值范围是.
∵
,,
∴
随的增大而增大,
∴
当时,有最大值,最大值(元),
此时,(台),
∴
该经销商分别购进空调扇和电风扇各台时,获利最大,最大利润为元.
18.
【答案】
解:∵
点在直线上,
故可设直线的表达式为.
又∵
点在直线上,
∴
,
∴
,
∴
直线的表达为?.?
过作轴交于,
∵
点的坐标为,
∴
点的纵坐标为.
当时,,
解得,
∴
,
∴
,
∴
.
∵
,
∴
,
解得或?.?
①当点在线段上时,
若点在,之间,
当,且时,
.
∵
,,
∴
.
设中边上的高为,
则,
∴
,
∴
,
∴
,
∴
点的横坐标为.
当时,,
∴
?
.?
若点在,之间,
当,且时有,
则,
∴
,
∴
.
作于,
则,
∴
,
∴
.
当时,?,
解得,
∴
.
②当点在的延长线上时,
若点在,之间,且,时,,
作于,于,
则,
∴
点的纵坐标为,
当时,,
解得,
∴
.
若点在的延长线上或的反向延长线上,都不存在满足条件的,两点.
综上所述,满足条件的点为,,.
【解答】
解:∵
点在直线上,
故可设直线的表达式为.
又∵
点在直线上,
∴
,
∴
,
∴
直线的表达为?.?
过作轴交于,
∵
点的坐标为,
∴
点的纵坐标为.
当时,,
解得,
∴
,
∴
,
∴
.
∵
,
∴
,
解得或?.?
①当点在线段上时,
若点在,之间,
当,且时,
.
∵
,,
∴
.
设中边上的高为,
则,
∴
,
∴
,
∴
,
∴
点的横坐标为.
当时,,
∴
?
.?
若点在,之间,
当,且时有,
则,
∴
,
∴
.
作于,
则,
∴
,
∴
.
当时,?,
解得,
∴
.
②当点在的延长线上时,
若点在,之间,且,时,,
作于,于,
则,
∴
点的纵坐标为,
当时,,
解得,
∴
.
若点在的延长线上或的反向延长线上,都不存在满足条件的,两点.
综上所述,满足条件的点为,,.
试卷第4页,总9页
试卷第5页,总9页
