人教版九年级下册数学学案:28.1 锐角三角函数(1)(无答案)
文档属性
| 名称 | 人教版九年级下册数学学案:28.1 锐角三角函数(1)(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 48.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览

文档简介
28.1
锐角三角函数(1)
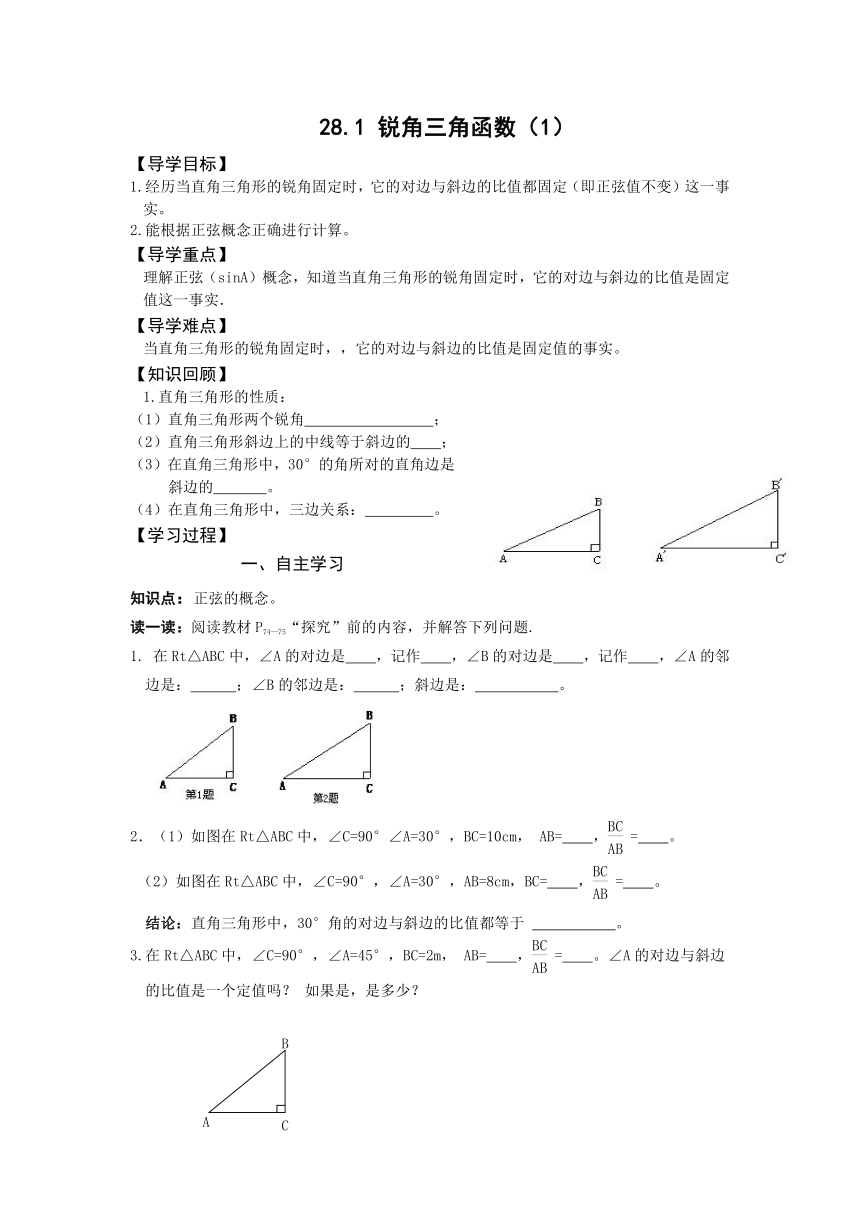
【导学目标】
1.经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实。
2.能根据正弦概念正确进行计算。
【导学重点】
理解正弦(sinA)概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实.
【导学难点】
当直角三角形的锐角固定时,,它的对边与斜边的比值是固定值的事实。
【知识回顾】
1.直角三角形的性质:
(1)直角三角形两个锐角
;
(2)直角三角形斜边上的中线等于斜边的
;
(3)在直角三角形中,30°的角所对的直角边是斜边的
。
(4)在直角三角形中,三边关系:
。
【学习过程】
一、自主学习
知识点:正弦的概念。
读一读:阅读教材P74—75“探究”前的内容,并解答下列问题.
1.
在Rt△ABC中,∠A的对边是
,记作
,∠B的对边是
,记作
,∠A的邻边是:
;∠B的邻边是:
;斜边是:
。
2.(1)如图在Rt△ABC中,∠C=90°∠A=30°,BC=10cm,
AB=
,=
。
(2)如图在Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,BC=
,=
。
结论:直角三角形中,30°角的对边与斜边的比值都等于
。
3.在Rt△ABC中,∠C=90°,∠A=45°,BC=2m,
AB=
,=
。∠A的对边与斜边的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,45°角的对边与斜边的比值都等于
。
读一读:阅读教材P75—77“练习”前的内容,并解答下列问题。
4.Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,
∠A=∠A′=,
。
结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个
。
归纳总结:正弦函数概念:
规定:在Rt△ABC中,∠C=90°,就把锐角A的
与
的比叫做∠A的正弦,记作
,即sinA=
=
.
例如,当∠A=30°时,我们有sinA=sin30°=
;当∠A=45°时,我们有sinA=sin45°=
.
注意事项:
1.sinA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA是一个比值(数值),所以没有单位。
3.sinA的大小只与∠A的大小有关,而与直角三角形边长无关
4.sinA是整体符号。不能写成sinA
5.当用一个字母表示角时,习惯省略角的符号“∠”,如:sinA。当用三个字母表示角时,角的符号“∠”不能省略,如必须写成sin∠ABC,不能写成sinABC。
练习:
1.判断对错
(1)
如图
sinA=
.
(
)
②sinB=
.
(
)
③sinA=0.6m
.
(
)
④sinB=0.8
.
(
)
(2)如图,sinA=.
(
)
2.结合例1的解题格式完成课本P77
练习。
二、合作探究
例1
如图,在△ABC中,
AB=6
AC=5,sinA=,求△ABC的面积。
例2
已知在Rt△ABC中,∠C=90°,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=,
AE=7,求DE的长.
锐角三角函数(1)
【导学目标】
1.经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实。
2.能根据正弦概念正确进行计算。
【导学重点】
理解正弦(sinA)概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实.
【导学难点】
当直角三角形的锐角固定时,,它的对边与斜边的比值是固定值的事实。
【知识回顾】
1.直角三角形的性质:
(1)直角三角形两个锐角
;
(2)直角三角形斜边上的中线等于斜边的
;
(3)在直角三角形中,30°的角所对的直角边是斜边的
。
(4)在直角三角形中,三边关系:
。
【学习过程】
一、自主学习
知识点:正弦的概念。
读一读:阅读教材P74—75“探究”前的内容,并解答下列问题.
1.
在Rt△ABC中,∠A的对边是
,记作
,∠B的对边是
,记作
,∠A的邻边是:
;∠B的邻边是:
;斜边是:
。
2.(1)如图在Rt△ABC中,∠C=90°∠A=30°,BC=10cm,
AB=
,=
。
(2)如图在Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,BC=
,=
。
结论:直角三角形中,30°角的对边与斜边的比值都等于
。
3.在Rt△ABC中,∠C=90°,∠A=45°,BC=2m,
AB=
,=
。∠A的对边与斜边的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,45°角的对边与斜边的比值都等于
。
读一读:阅读教材P75—77“练习”前的内容,并解答下列问题。
4.Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,
∠A=∠A′=,
。
结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个
。
归纳总结:正弦函数概念:
规定:在Rt△ABC中,∠C=90°,就把锐角A的
与
的比叫做∠A的正弦,记作
,即sinA=
=
.
例如,当∠A=30°时,我们有sinA=sin30°=
;当∠A=45°时,我们有sinA=sin45°=
.
注意事项:
1.sinA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA是一个比值(数值),所以没有单位。
3.sinA的大小只与∠A的大小有关,而与直角三角形边长无关
4.sinA是整体符号。不能写成sinA
5.当用一个字母表示角时,习惯省略角的符号“∠”,如:sinA。当用三个字母表示角时,角的符号“∠”不能省略,如必须写成sin∠ABC,不能写成sinABC。
练习:
1.判断对错
(1)
如图
sinA=
.
(
)
②sinB=
.
(
)
③sinA=0.6m
.
(
)
④sinB=0.8
.
(
)
(2)如图,sinA=.
(
)
2.结合例1的解题格式完成课本P77
练习。
二、合作探究
例1
如图,在△ABC中,
AB=6
AC=5,sinA=,求△ABC的面积。
例2
已知在Rt△ABC中,∠C=90°,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=,
AE=7,求DE的长.
