人教版数学八年级上册 第12章 12.2三角形全等的判定同步测试题(word解析版)
文档属性
| 名称 | 人教版数学八年级上册 第12章 12.2三角形全等的判定同步测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 226.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 23:39:51 | ||
图片预览


文档简介
三角形全等的判定同步测试题(一)
一.选择题
1.不能判断两个三个角形全等的条件是( )
A.有三条边对应相等
B.有两边及夹角对应相等
C.有两角及一边相等
D.有两个角及夹边对应相等
2.如图,已知∠1=∠2,则不一定能使△ABC≌△BAD的条件是( )
A.∠C=∠D
B.AD=BC
C.AC=BD
D.∠3=∠4
3.已知:如图,点B,F,C,E在同一条直线上,AC∥DF,AC=DF.添加下列选项中的一个条件,仍不能使的是△ABC≌△DEF的是( )
A.AB=DE
B.BF=CE
C.∠B=∠E
D.∠A=∠D
4.如图,已知,∠CAB=∠DAE,AC=AD,增加下列条件:①AB=AE;
②BC=ED;
③∠C=∠D;④∠B=∠E;⑤∠1=∠2.其中能使△ABC≌△AED的条件有( )
A.2个
B.3个
C.4个
D.5个
5.如图,∠1=∠2,∠3=∠4,则判定两个三角形全等的依据是( )
A.SSS
B.ASA
C.SAS
D.AAS
6.下列说法正确的是哪一项( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.两个等腰三角形是全等三角形
D.全等三角形的周长、面积分别相等
7.如图,点E、F在线段BD上,AB=CD,且AE⊥BD,CF⊥BD,如果再添加一个条件使△ABE≌△CDF,不正确的是( )
A.∠A=∠C
B.AB∥CD
C.DE=BF
D.AE∥CF
8.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件不能判定Rt△ABC≌Rt△DEF的是( )
A.AC=DF,∠B=∠E
B.∠A=∠D,∠B=∠E
C.AB=DE,AC=DF
D.AB=DE,∠A=∠D
9.如图,AB∥CD,BC∥AD,AB=CD,AE=CF,其中全等三角形的对数是( )
A.4
B.3
C.2
D.1
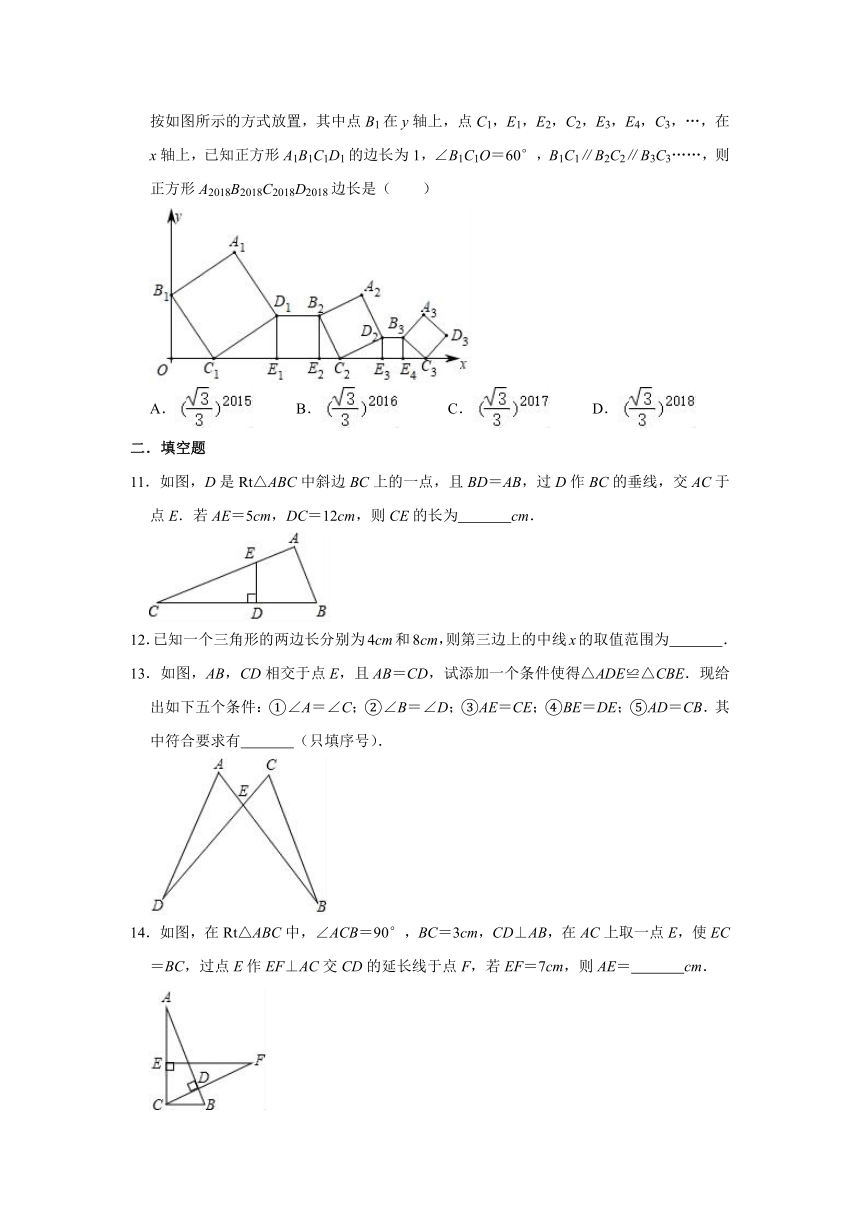
10.在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2B2C2D2,D2E3E4B3,A3B3C3D3…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2018B2018C2018D2018边长是( )
A.
B.
C.
D.
二.填空题
11.如图,D是Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于点E.若AE=5cm,DC=12cm,则CE的长为
cm.
12.已知一个三角形的两边长分别为4cm和8cm,则第三边上的中线x的取值范围为
.
13.如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有
(只填序号).
14.如图,在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE=
cm.
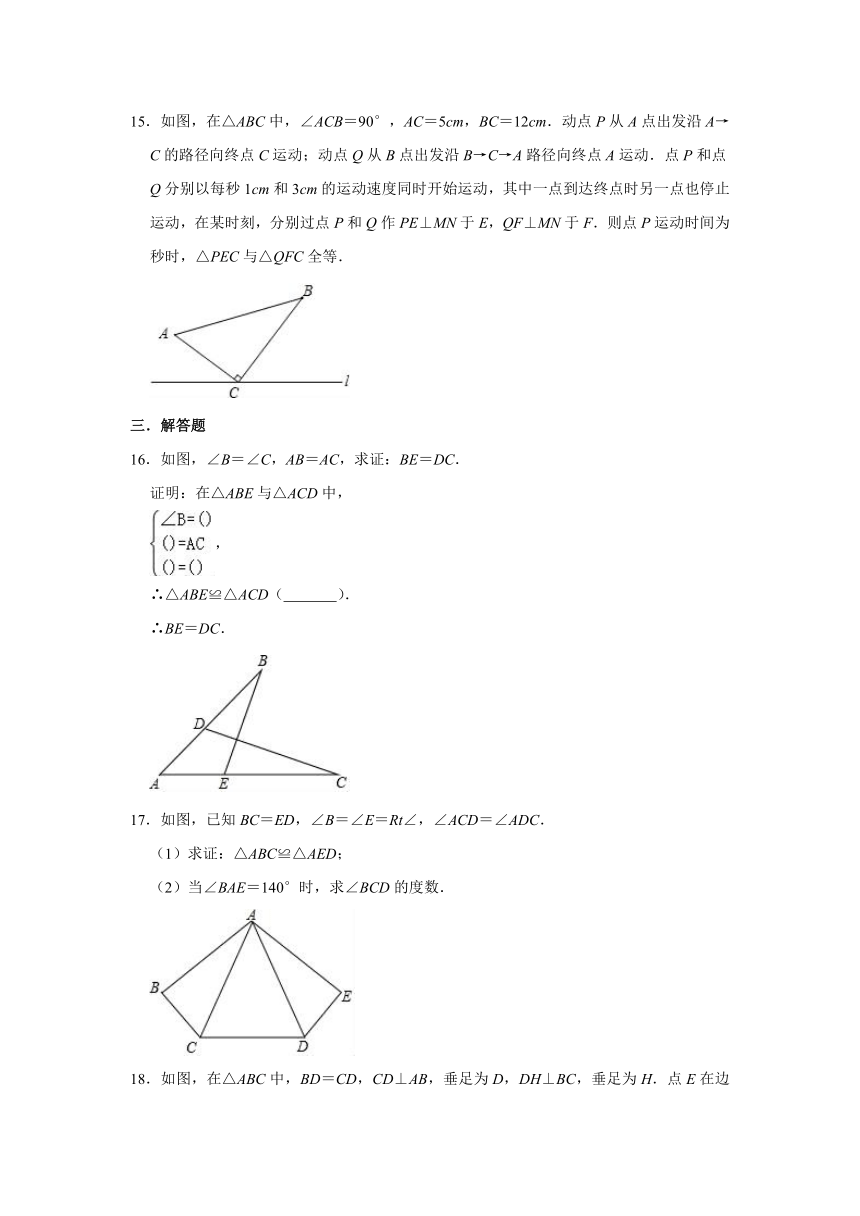
15.如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm.动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E,QF⊥MN于F.则点P运动时间为
秒时,△PEC与△QFC全等.
三.解答题
16.如图,∠B=∠C,AB=AC,求证:BE=DC.
证明:在△ABE与△ACD中,
,
∴△ABE≌△ACD(
).
∴BE=DC.
17.如图,已知BC=ED,∠B=∠E=Rt∠,∠ACD=∠ADC.
(1)求证:△ABC≌△AED;
(2)当∠BAE=140°时,求∠BCD的度数.
18.如图,在△ABC中,BD=CD,CD⊥AB,垂足为D,DH⊥BC,垂足为H.点E在边AC上,BE分别与CD、DH相交于点F、G.
(1)求证:BG=CG;
(2)若AB=BC,且BE⊥AC.求证:BG=CE+EF.
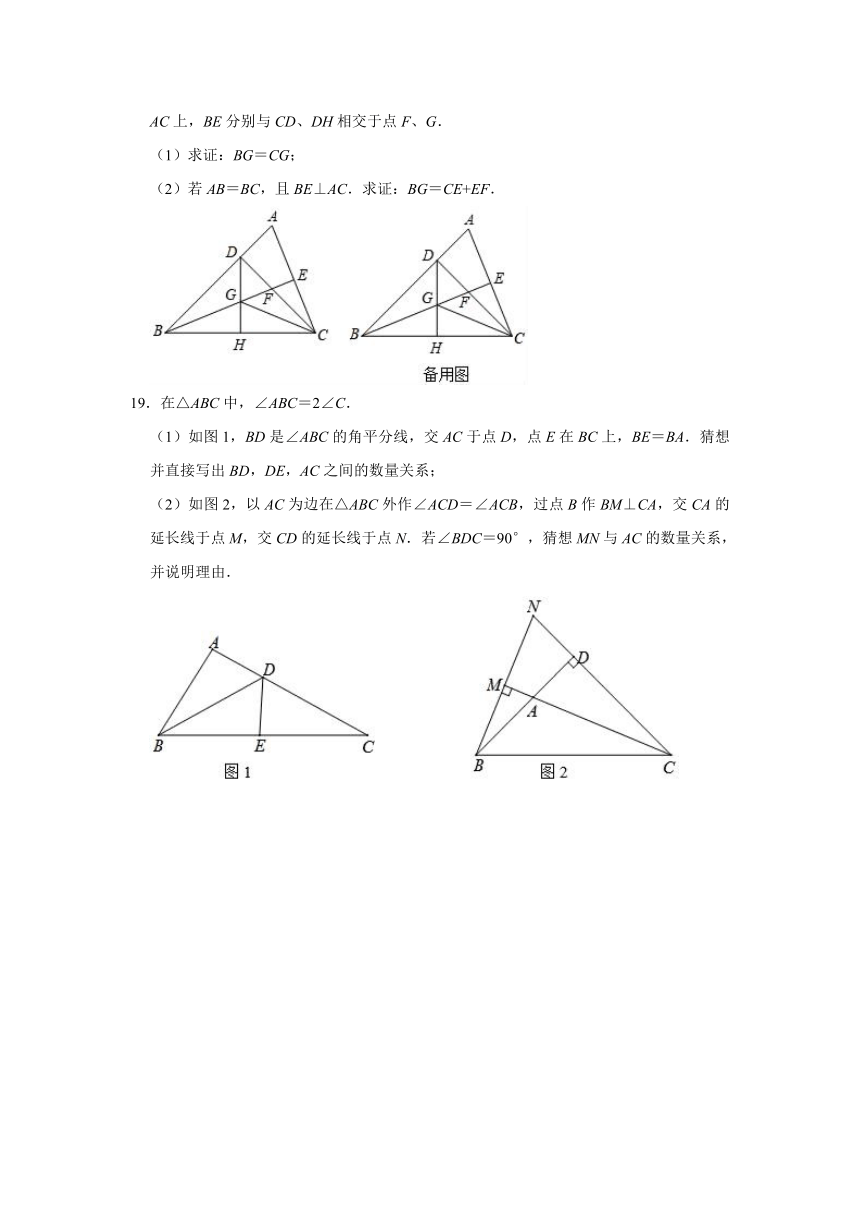
19.在△ABC中,∠ABC=2∠C.
(1)如图1,BD是∠ABC的角平分线,交AC于点D,点E在BC上,BE=BA.猜想并直接写出BD,DE,AC之间的数量关系;
(2)如图2,以AC为边在△ABC外作∠ACD=∠ACB,过点B作BM⊥CA,交CA的延长线于点M,交CD的延长线于点N.若∠BDC=90°,猜想MN与AC的数量关系,并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、符合全等三角形的判定定理SSS,故本选项不合题意;
B、符合全等三角形的判定定理SAS,故本选项不合题意;
C、不符合全等三角形的判定定理,故本选项符合题意;
D、符合全等三角形的判定定理ASA,故本选项不合题意;
故选:C.
2.【解答】解:A、∵∠1=∠2,AB为公共边,若∠C=∠D,则△ABC≌△ABD(AAS),故本选项错误;
B、∵∠1=∠2,AB为公共边,若AD=BC,则△ABC≌△ABD(SAS),故本选项错误;
C、∵∠1=∠2,AB为公共边,若AC=BD,则不能使△ABC≌△ABD,故本选项正确;
D、∵∠1=∠2,AB为公共边,若∠3=∠4,则△ABC≌△ABD(ASA),故本选项错误;
故选:C.
3.【解答】解:已知条件知:∠ACB=∠DFE,AC=DF.
A、当添加AB=DE时,根据SSA不能判定△ABC≌△DEF,故本选项符合题意;
B、当添加BF=CE时,则BC=EF,根据SAS能判定△ABC≌△DEF,故本选项不符合题意;
C、当添加∠B=∠E时,根据AAS能判定△ABC≌△DEF,故本选项不符合题意;
D、当添加∠A=∠D时,根据ASA能判定△ABC≌△DEF,故本选项不符合题意;
故选:A.
4.【解答】解:∵∠CAB=∠DAE,AC=AD,
∴①加上条件AB=AE可利用SAS定理证明△ABC≌△AED;
②加上BC=ED不能证明△ABC≌△AED;
③加上∠C=∠D可利用ASA证明△ABC≌△AED;
④加上∠B=∠E可利用AAS证明△ABC≌△AED;
⑤加上∠1=∠2不能证明△ABC≌△AED;
故选:B.
5.【解答】解:∵∠1=∠2,∠3=∠4,AD=AD
∴△ABD≌△ACD.(ASA)
故选:B.
6.【解答】解:A、全等三角形是指形状、大小相同的两个三角形,错误;
B、全等三角形是指形状、大小相同的两个三角形,错误;
C、两个等腰三角形不一定是全等三角形,错误;
D、全等三角形的周长、面积分别相等,正确;
故选:D.
7.【解答】解:∵AB=CD,AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
当添加∠A=∠C时,由AAS判定△ABE≌△CDF,
∴选项A正确;
当添加AB∥CD时,∴∠B=∠D,由AAS判定△ABE≌△CDF,
∴选项B正确;
当添加DE=BF时,∴DF=BE,由HL判定△ABE≌△CDF,
∴选项C正确;
当AE∥CF,∴∠AEB=∠CFD,不能判定△ABE≌△CDF,
∴选项D不正确;
故选:D.
8.【解答】解:
A、∵在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(AAS),故本选项不符合题意;
B、在Rt△ABC和Rt△DEF中,根据∠A=∠D、∠C=∠F、∠B=∠E不能推出两三角形全等,故本选项符合题意;
C、∵在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL),故本选项不符合题意;
D、∵在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(AAS),故本选项不符合题意;
故选:B.
9.【解答】解:∵AB∥CD,BC∥AD,
∴∠BAC=∠ACD,∠DAC=∠ACB.
在△ABC和△CDA中
,
∴△ABC≌△CDA(ASA),
∴AD=BC,AB=CD.
在△ABE和△CDF中
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
∵AE=CF,
∴AE+EF=CE+EF,
∴AF=CE,
在△ADF和△CBE中
,
∴△ADF≌△CBE(SSS),
即3对全等三角形,
故选:B.
10.【解答】解:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=,则B2C2=()1,
同理可得:B3C3==()2,
故正方形AnBn?nDn的边长是:()n﹣1.
则正方形A2018B2018C2018D2018的边长是:()2017.
故选:C.
二.填空题(共5小题)
11.【解答】解:连接BE,
∵D是Rt△ABC中斜边BC上的一点,过D作BC的垂线,
∴∠EDC=90°,∠EDB=∠A=90°,
在Rt△EDB和Rt△EAB中
∴Rt△EDB≌Rt△EAB(HL),
∴AE=DE,
∵AE=5cm,
∴DE=5cm,
在Rt△EDC中,ED=5cm,DC=12cm,由勾股定理得:CE==13cm,
故答案为:13.
12.【解答】解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
∵,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵三角形两边长为4,8,第三边上的中线为x,
∴8﹣4<2x<8+4,即4<2x<12,
∴2<x<6.
故答案为:2<x<6.
13.【解答】解:延长DA,BC使它们相交于点F.
∵∠DAB=∠BCD,∠AED=∠BEC,
∴∠B=∠D,
又∵∠F=∠F,AB=CD,
∴△FAB≌△FCD
∴AF=FC,FD=FB,
∴AD=BC,
∴△ADE≌△CBE(AAS)①对
同理可得②对,
∵AE=CE,AB=CD,
∴DE=BE,
又∵∠AED=∠BEC,
∴△ADE≌△CBE(SAS)③对,
同理可得④对,
连接BD,∵AD=CB,AB=CD,BD=BD,
∴△ADB≌△CBD(SSS),
∴∠A=∠C,
∴△ADE≌△CBE,故⑤正确,
故答案为①②③④⑤.
14.【解答】解:∵EF⊥AC,
∴∠FEC=90°,
∵CD⊥AB,
∴∠ADF=90°,
∴∠A=∠F,
在△ACB和△FEC中
,
∴△ACB≌△FEC(AAS),
∴AC=EF=7cm,
而EC=BC=3cm,
∴AE=7cm﹣3cm=4cm.
故答案为4.
15.【解答】解:设运动时间为t秒时,△PEC≌△QFC,
∵△PEC≌△QFC,
∴斜边CP=CQ,
有2种情况:①如图1,点P在AC上,点Q在BC上,
CP=5﹣t,CQ=12﹣3t,
∴5﹣t=12﹣3t,
∴t=;
②如图2,点P、Q都在AC上,此时点P、Q重合,
∴CP=5﹣t=3t﹣12,
∴t=;
综上所述,点P运动时间为或秒时,△PEC与△QFC全等,
故答案为:或.
三.解答题(共4小题)
16.【解答】解:如图,
证明:△ABE与△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=DC.
故答案为:∠C,AB,∠DAC=∠EAB,ASA.
17.【解答】证明:(1)∵∠ACD=∠ADC,
∴AC=AD,
在Rt△ABC和Rt△AED中,
∵,
∴Rt△ABC≌Rt△AED(HL);
(2)∵Rt△ABC≌Rt△AED,
∴可设∠BAC=∠EAD=x,∠CAD=y,
∵∠BAE=140°,
∴2x+y=140°,
∵∠B=90°,
∴∠ACB=90°﹣x,
又∵AC=AD,
∴∠ACD=∠ADC==90°﹣y,
则∠BCD=∠ACB+∠ACD
=90°﹣x+90°﹣y
=180°﹣(2x+y)
=180°﹣70°
=110°.
18.【解答】证明:(1)∵CD⊥AB,
∴∠CDB=90°,
∵BD=CD,
∵DH⊥BC,
∴BH=CH,
∴GB=GC;
(2)∵BA=BC,BE⊥AC,∠ABC=45°,
∴∠ABE=∠CBE=22.5°,
在AE上取点N,使得EN=EF,连接FN,如备用图,
∴∠ENF=∠EFN=45°,
∵GB=GC,
∴∠GBC=∠GCB=22.5°,
∴∠FGC=∠GBC+∠GCB=45°,
∴∠FGC=∠FNC=45°,
∵∠CFE=∠CBF+∠BCF=67.5°,
∴∠CFG=180°﹣∠CFE=112.5°,
∠CFN=∠CFE+∠EFN=112.5°,
∴∠CFG=∠CFN,
∵CF=CF,
∴△CFG≌△CFN(AAS),
∴CG=CN=CE+EN,
∵CG=BG,EN=EF,
∴BG=CE+EF.
19.【解答】解:(1)BD+DE=AC,
理由如下:
∵BD是∠ABC的角平分线,
∴∠ABD=∠EBD,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(SAS),
∴AD=ED,
∵∠ABC=2∠C,
∴∠DBC=∠C,
∴DB=DC,
∴BD+DE=DC+AD=AC,
即BD+DE=AC;
(2)MN=AC.
理由如下:
∵∠ABC=2∠ACB,∠ACD=∠ACB.
∴∠ABC=∠BCD.
∴DB=DC.
∵BM⊥CA,
∴∠BMC=90°.
∵∠BDC=90°,
∴∠N+∠MCN=∠DAC+∠MCN,∠BDN=90°.
∴∠N=∠DAC.
在△ACD和△NBD中,
∴△ACD≌△NBD(AAS).
∴AC=NB.
∵CM⊥BN,
∴∠CMB=∠CMN=90°,
∵CM=CM,∠NCM=∠BCM,
∴△CMB≌△CMN(ASA),
∴BM=NM,
∴MN=BN.
∴MN=AC.
一.选择题
1.不能判断两个三个角形全等的条件是( )
A.有三条边对应相等
B.有两边及夹角对应相等
C.有两角及一边相等
D.有两个角及夹边对应相等
2.如图,已知∠1=∠2,则不一定能使△ABC≌△BAD的条件是( )
A.∠C=∠D
B.AD=BC
C.AC=BD
D.∠3=∠4
3.已知:如图,点B,F,C,E在同一条直线上,AC∥DF,AC=DF.添加下列选项中的一个条件,仍不能使的是△ABC≌△DEF的是( )
A.AB=DE
B.BF=CE
C.∠B=∠E
D.∠A=∠D
4.如图,已知,∠CAB=∠DAE,AC=AD,增加下列条件:①AB=AE;
②BC=ED;
③∠C=∠D;④∠B=∠E;⑤∠1=∠2.其中能使△ABC≌△AED的条件有( )
A.2个
B.3个
C.4个
D.5个
5.如图,∠1=∠2,∠3=∠4,则判定两个三角形全等的依据是( )
A.SSS
B.ASA
C.SAS
D.AAS
6.下列说法正确的是哪一项( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.两个等腰三角形是全等三角形
D.全等三角形的周长、面积分别相等
7.如图,点E、F在线段BD上,AB=CD,且AE⊥BD,CF⊥BD,如果再添加一个条件使△ABE≌△CDF,不正确的是( )
A.∠A=∠C
B.AB∥CD
C.DE=BF
D.AE∥CF
8.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件不能判定Rt△ABC≌Rt△DEF的是( )
A.AC=DF,∠B=∠E
B.∠A=∠D,∠B=∠E
C.AB=DE,AC=DF
D.AB=DE,∠A=∠D
9.如图,AB∥CD,BC∥AD,AB=CD,AE=CF,其中全等三角形的对数是( )
A.4
B.3
C.2
D.1
10.在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2B2C2D2,D2E3E4B3,A3B3C3D3…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2018B2018C2018D2018边长是( )
A.
B.
C.
D.
二.填空题
11.如图,D是Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于点E.若AE=5cm,DC=12cm,则CE的长为
cm.
12.已知一个三角形的两边长分别为4cm和8cm,则第三边上的中线x的取值范围为
.
13.如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有
(只填序号).
14.如图,在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE=
cm.
15.如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm.动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E,QF⊥MN于F.则点P运动时间为
秒时,△PEC与△QFC全等.
三.解答题
16.如图,∠B=∠C,AB=AC,求证:BE=DC.
证明:在△ABE与△ACD中,
,
∴△ABE≌△ACD(
).
∴BE=DC.
17.如图,已知BC=ED,∠B=∠E=Rt∠,∠ACD=∠ADC.
(1)求证:△ABC≌△AED;
(2)当∠BAE=140°时,求∠BCD的度数.
18.如图,在△ABC中,BD=CD,CD⊥AB,垂足为D,DH⊥BC,垂足为H.点E在边AC上,BE分别与CD、DH相交于点F、G.
(1)求证:BG=CG;
(2)若AB=BC,且BE⊥AC.求证:BG=CE+EF.
19.在△ABC中,∠ABC=2∠C.
(1)如图1,BD是∠ABC的角平分线,交AC于点D,点E在BC上,BE=BA.猜想并直接写出BD,DE,AC之间的数量关系;
(2)如图2,以AC为边在△ABC外作∠ACD=∠ACB,过点B作BM⊥CA,交CA的延长线于点M,交CD的延长线于点N.若∠BDC=90°,猜想MN与AC的数量关系,并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、符合全等三角形的判定定理SSS,故本选项不合题意;
B、符合全等三角形的判定定理SAS,故本选项不合题意;
C、不符合全等三角形的判定定理,故本选项符合题意;
D、符合全等三角形的判定定理ASA,故本选项不合题意;
故选:C.
2.【解答】解:A、∵∠1=∠2,AB为公共边,若∠C=∠D,则△ABC≌△ABD(AAS),故本选项错误;
B、∵∠1=∠2,AB为公共边,若AD=BC,则△ABC≌△ABD(SAS),故本选项错误;
C、∵∠1=∠2,AB为公共边,若AC=BD,则不能使△ABC≌△ABD,故本选项正确;
D、∵∠1=∠2,AB为公共边,若∠3=∠4,则△ABC≌△ABD(ASA),故本选项错误;
故选:C.
3.【解答】解:已知条件知:∠ACB=∠DFE,AC=DF.
A、当添加AB=DE时,根据SSA不能判定△ABC≌△DEF,故本选项符合题意;
B、当添加BF=CE时,则BC=EF,根据SAS能判定△ABC≌△DEF,故本选项不符合题意;
C、当添加∠B=∠E时,根据AAS能判定△ABC≌△DEF,故本选项不符合题意;
D、当添加∠A=∠D时,根据ASA能判定△ABC≌△DEF,故本选项不符合题意;
故选:A.
4.【解答】解:∵∠CAB=∠DAE,AC=AD,
∴①加上条件AB=AE可利用SAS定理证明△ABC≌△AED;
②加上BC=ED不能证明△ABC≌△AED;
③加上∠C=∠D可利用ASA证明△ABC≌△AED;
④加上∠B=∠E可利用AAS证明△ABC≌△AED;
⑤加上∠1=∠2不能证明△ABC≌△AED;
故选:B.
5.【解答】解:∵∠1=∠2,∠3=∠4,AD=AD
∴△ABD≌△ACD.(ASA)
故选:B.
6.【解答】解:A、全等三角形是指形状、大小相同的两个三角形,错误;
B、全等三角形是指形状、大小相同的两个三角形,错误;
C、两个等腰三角形不一定是全等三角形,错误;
D、全等三角形的周长、面积分别相等,正确;
故选:D.
7.【解答】解:∵AB=CD,AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
当添加∠A=∠C时,由AAS判定△ABE≌△CDF,
∴选项A正确;
当添加AB∥CD时,∴∠B=∠D,由AAS判定△ABE≌△CDF,
∴选项B正确;
当添加DE=BF时,∴DF=BE,由HL判定△ABE≌△CDF,
∴选项C正确;
当AE∥CF,∴∠AEB=∠CFD,不能判定△ABE≌△CDF,
∴选项D不正确;
故选:D.
8.【解答】解:
A、∵在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(AAS),故本选项不符合题意;
B、在Rt△ABC和Rt△DEF中,根据∠A=∠D、∠C=∠F、∠B=∠E不能推出两三角形全等,故本选项符合题意;
C、∵在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL),故本选项不符合题意;
D、∵在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(AAS),故本选项不符合题意;
故选:B.
9.【解答】解:∵AB∥CD,BC∥AD,
∴∠BAC=∠ACD,∠DAC=∠ACB.
在△ABC和△CDA中
,
∴△ABC≌△CDA(ASA),
∴AD=BC,AB=CD.
在△ABE和△CDF中
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
∵AE=CF,
∴AE+EF=CE+EF,
∴AF=CE,
在△ADF和△CBE中
,
∴△ADF≌△CBE(SSS),
即3对全等三角形,
故选:B.
10.【解答】解:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=,则B2C2=()1,
同理可得:B3C3==()2,
故正方形AnBn?nDn的边长是:()n﹣1.
则正方形A2018B2018C2018D2018的边长是:()2017.
故选:C.
二.填空题(共5小题)
11.【解答】解:连接BE,
∵D是Rt△ABC中斜边BC上的一点,过D作BC的垂线,
∴∠EDC=90°,∠EDB=∠A=90°,
在Rt△EDB和Rt△EAB中
∴Rt△EDB≌Rt△EAB(HL),
∴AE=DE,
∵AE=5cm,
∴DE=5cm,
在Rt△EDC中,ED=5cm,DC=12cm,由勾股定理得:CE==13cm,
故答案为:13.
12.【解答】解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
∵,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵三角形两边长为4,8,第三边上的中线为x,
∴8﹣4<2x<8+4,即4<2x<12,
∴2<x<6.
故答案为:2<x<6.
13.【解答】解:延长DA,BC使它们相交于点F.
∵∠DAB=∠BCD,∠AED=∠BEC,
∴∠B=∠D,
又∵∠F=∠F,AB=CD,
∴△FAB≌△FCD
∴AF=FC,FD=FB,
∴AD=BC,
∴△ADE≌△CBE(AAS)①对
同理可得②对,
∵AE=CE,AB=CD,
∴DE=BE,
又∵∠AED=∠BEC,
∴△ADE≌△CBE(SAS)③对,
同理可得④对,
连接BD,∵AD=CB,AB=CD,BD=BD,
∴△ADB≌△CBD(SSS),
∴∠A=∠C,
∴△ADE≌△CBE,故⑤正确,
故答案为①②③④⑤.
14.【解答】解:∵EF⊥AC,
∴∠FEC=90°,
∵CD⊥AB,
∴∠ADF=90°,
∴∠A=∠F,
在△ACB和△FEC中
,
∴△ACB≌△FEC(AAS),
∴AC=EF=7cm,
而EC=BC=3cm,
∴AE=7cm﹣3cm=4cm.
故答案为4.
15.【解答】解:设运动时间为t秒时,△PEC≌△QFC,
∵△PEC≌△QFC,
∴斜边CP=CQ,
有2种情况:①如图1,点P在AC上,点Q在BC上,
CP=5﹣t,CQ=12﹣3t,
∴5﹣t=12﹣3t,
∴t=;
②如图2,点P、Q都在AC上,此时点P、Q重合,
∴CP=5﹣t=3t﹣12,
∴t=;
综上所述,点P运动时间为或秒时,△PEC与△QFC全等,
故答案为:或.
三.解答题(共4小题)
16.【解答】解:如图,
证明:△ABE与△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=DC.
故答案为:∠C,AB,∠DAC=∠EAB,ASA.
17.【解答】证明:(1)∵∠ACD=∠ADC,
∴AC=AD,
在Rt△ABC和Rt△AED中,
∵,
∴Rt△ABC≌Rt△AED(HL);
(2)∵Rt△ABC≌Rt△AED,
∴可设∠BAC=∠EAD=x,∠CAD=y,
∵∠BAE=140°,
∴2x+y=140°,
∵∠B=90°,
∴∠ACB=90°﹣x,
又∵AC=AD,
∴∠ACD=∠ADC==90°﹣y,
则∠BCD=∠ACB+∠ACD
=90°﹣x+90°﹣y
=180°﹣(2x+y)
=180°﹣70°
=110°.
18.【解答】证明:(1)∵CD⊥AB,
∴∠CDB=90°,
∵BD=CD,
∵DH⊥BC,
∴BH=CH,
∴GB=GC;
(2)∵BA=BC,BE⊥AC,∠ABC=45°,
∴∠ABE=∠CBE=22.5°,
在AE上取点N,使得EN=EF,连接FN,如备用图,
∴∠ENF=∠EFN=45°,
∵GB=GC,
∴∠GBC=∠GCB=22.5°,
∴∠FGC=∠GBC+∠GCB=45°,
∴∠FGC=∠FNC=45°,
∵∠CFE=∠CBF+∠BCF=67.5°,
∴∠CFG=180°﹣∠CFE=112.5°,
∠CFN=∠CFE+∠EFN=112.5°,
∴∠CFG=∠CFN,
∵CF=CF,
∴△CFG≌△CFN(AAS),
∴CG=CN=CE+EN,
∵CG=BG,EN=EF,
∴BG=CE+EF.
19.【解答】解:(1)BD+DE=AC,
理由如下:
∵BD是∠ABC的角平分线,
∴∠ABD=∠EBD,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(SAS),
∴AD=ED,
∵∠ABC=2∠C,
∴∠DBC=∠C,
∴DB=DC,
∴BD+DE=DC+AD=AC,
即BD+DE=AC;
(2)MN=AC.
理由如下:
∵∠ABC=2∠ACB,∠ACD=∠ACB.
∴∠ABC=∠BCD.
∴DB=DC.
∵BM⊥CA,
∴∠BMC=90°.
∵∠BDC=90°,
∴∠N+∠MCN=∠DAC+∠MCN,∠BDN=90°.
∴∠N=∠DAC.
在△ACD和△NBD中,
∴△ACD≌△NBD(AAS).
∴AC=NB.
∵CM⊥BN,
∴∠CMB=∠CMN=90°,
∵CM=CM,∠NCM=∠BCM,
∴△CMB≌△CMN(ASA),
∴BM=NM,
∴MN=BN.
∴MN=AC.
