1.4空间图形的基本关系与公理
图片预览


文档简介
空间图形的基本关系与公理
一. 教学内容:
空间图形的基本关系与公理
二. 学习目标:
1、学会观察长方体模型中点、线、面之间的关系,并能结合长方体模型,掌握空间图形的有关概念和有关定理;掌握平面的基本性质、公理4和等角定理;
2、培养和发展自己的空间想象能力、运用图形语言进行交流的能力、几何直观能力、通过典型例子的学习和自主探索活动,理解数学概念和结论,体会蕴涵在其中的数学思想方法;
3、培养严谨的思维习惯与严肃的科学态度;体会推理论证中反映出的辩证思维的价值观。
三、知识要点
(一)空间位置关系:
I、空间点与线的关系
空间点与直线的位置关系有两种: 点P在直线上:; 点P在直线外:;
II、空间点与平面的关系
空间点与平面的位置关系有两种: 点P在平面上: 点P在平面外:;
III、空间直线与直线的位置关系:
IV、空间直线与平面的位置关系:
V、空间平面与平面的位置关系: 平行; 相交
说明:本模块中所说的“两个平面”“两条直线”等均指不重合的情形。
(二)异面直线的判定
1、定义法:采取反证法的思路,否定平行与相交两种情形即可;
2、判定定理:已知P点在平面上,则平面上不经过该点的直线与平面外经过该点的直线是异面直线。
(三)平面的基本性质公理
1、公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内(即直线在平面内,或曰平面经过这条直线)。
2、公理2 经过不在同一条直线上的三点,有且只有一个平面(即确定一个平面)。
3、公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条通过该点的公共直线。
4、平面的基本性质公理的三个推论
经过直线和直线外一点,有且只有一个平面;
经过两条相交直线,有且只有一个平面;
经过两条平行直线,有且只有一个平面
思考:
公理是公认为正确而不需要证明的命题,那么推论呢?
平面的基本性质公理是如何刻画平面的性质的?
(四)平行公理(公理4):平行于同一条直线的两条直线平行。
(五)等角定理:空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补。
(六)空间四边形:顺次连接不共面的四点构成的图形称为空间四边形。
【典型例题】
考点一 空间点线面位置关系的判断:主要判断依据是平面的基本性质公理及其推论,平行公理、等角定理等相关结论。
例1. 下列命题:
空间不同的三点可以确定一个平面;
有三个公共点的两个平面必定重合;
空间中两两相交的三条直线可以确定一个平面;
④平行四边形、梯形等所有的四边形都是平面图形;
⑤两组对边分别相等的四边形是平行四边形;
⑥一条直线和两平行线中的一条相交,必定和另一条也相交。
其中正确的命题是 。
解:⑥。
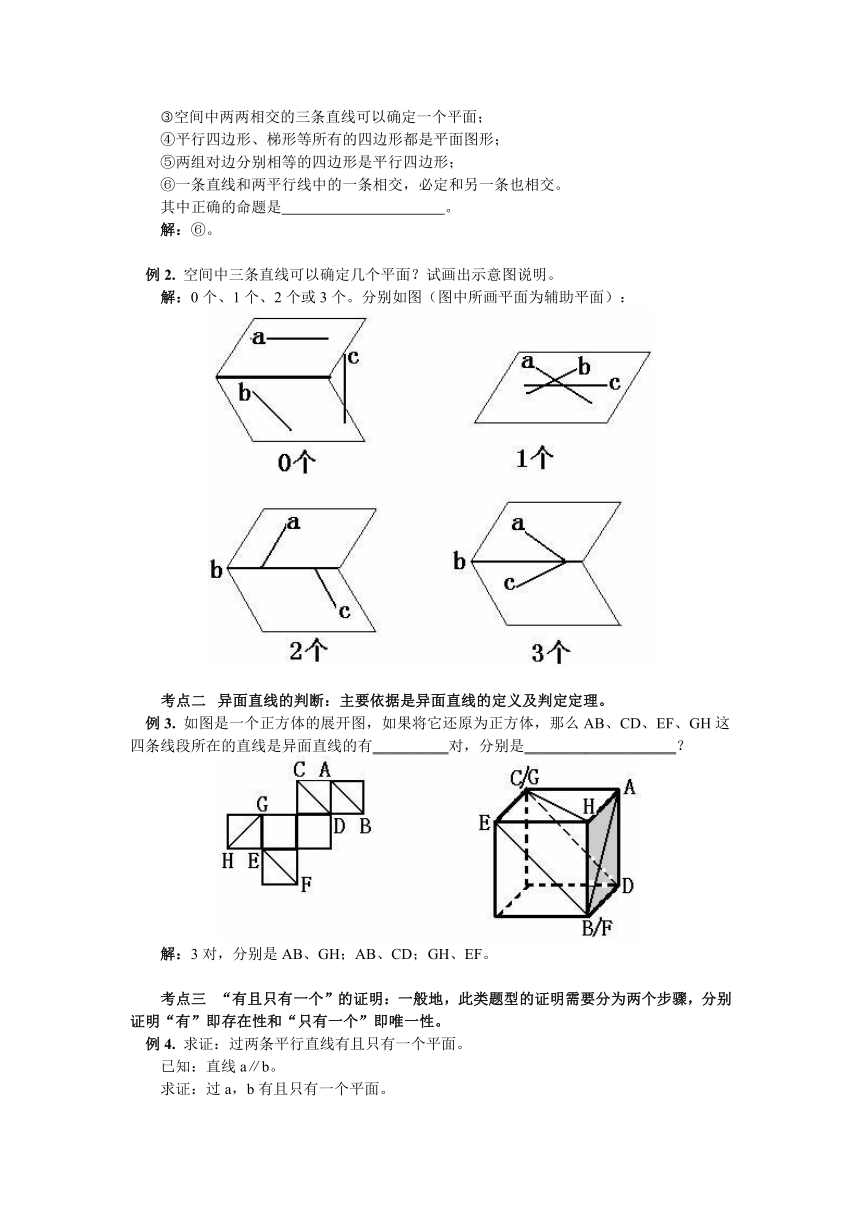
例2. 空间中三条直线可以确定几个平面?试画出示意图说明。
解:0个、1个、2个或3个。分别如图(图中所画平面为辅助平面):
考点二 异面直线的判断:主要依据是异面直线的定义及判定定理。
例3. 如图是一个正方体的展开图,如果将它还原为正方体,那么AB、CD、EF、GH这四条线段所在的直线是异面直线的有__________对,分别是____________________?
解:3对,分别是AB、GH;AB、CD;GH、EF。
考点三 “有且只有一个”的证明:一般地,此类题型的证明需要分为两个步骤,分别证明“有”即存在性和“只有一个”即唯一性。
例4. 求证:过两条平行直线有且只有一个平面。
已知:直线a∥b。
求证:过a,b有且只有一个平面。
证明: 存在性:由平行线的定义可知,过平行直线a,b有一个平面。
唯一性(反证法):假设过a,b有两个平面。在直线上任取两点A、B,在直线b上任取一点C,则A、B、C三点不共线。由于这两个平面都过直线a,b,因此由公理1可知:都过点A、B、C。由平面的基本性质公理2,过不共线三点的平面唯一存在,因此重合,与假设矛盾。矛盾表明:过平行直线a,b只有一个平面。
综上所述:过a,b有且只有一个平面。
考点四 共点的判断与证明:此类题型主要有三线共点和三面共点。
例5. 三个平面两两相交有三条交线,求证:三条交线或平行,或交于一点。
已知:平面,求证:a∥b∥c或者a,b,c交于一点P。
证明:因为,故a,b共面。
I、若a∥b:由于,故,因直线,故a,c无公共点。又a,c都在平面内,故a∥b;故a∥b∥c。
II、若,则,故知
综上所述:命题成立。
说明:证明三点共线的问题的常用思路是先证两条直线相交,然后再证该交点在第三条直线上;证明交点在第三条直线上常证明该点是两个相交平面的公共点,从而在这两个平面的交线上即在第三条直线上。
考点五 共线的判断与证明:常见题型是三点共线。
例6. 如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线。
证明:连结AC.因为A1C1∩B1D1=O1,B1D1平面B1D1A,A1C1AA1C1C,所以O1∈平面B1D1A且O1∈AA1C1C。同理可知,M∈平面B1D1A且M∈AA1C1C;A∈平面B1D1A且A∈AA1C1C。所以,O1、M、A三点在平面B1D1A和AA1C1C的交线上,故O1、M、A三点共线。
说明:证明三线共点问题的常见思路是证明第三点在前两点所确定的直线上;或者证明三点是两相交平面的公共点,从而在这两个平面的交线上。
考点六 共面问题的判断与证明:此类题型常见的是四点共面或三线共面,如证明某个图形是平面图形。
例7. 如图,在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且CG=BC/3,CH=DC/3。求证: E、F、G、H四点共面; 直线FH、EG、AC共点。
证明: 如图,连结HG,EF。在△ABD中,E、F分别为AB、AD中点,故EF是△ABD的中位线,故EF∥BD。在△CBD中,CG=BC/3,CH=DC/3,故GH∥BD,故EF∥GH,从而GH、EF可确定一个平面,即G、H、E、F四点共面。
由于E、F、G、H四点共面,且FH与EG不平行,故相交,记交点为M,则M∈FH,FH面ACD,故M∈面ACD;M∈EG,EG面ABC,故M∈面ABC。从而M是面ACD和面ABC的公共点,由公理3可知,M在这两个平面的交线AC上,从而FH、EG、AC三线共点。
说明:共面问题的常用的处理方法是利用平面的基本性质公理2及三个推论,先证明部分元素确定一个平面,再证剩下的元素也在此平面上;有时也可先证部分元素共面,剩下的元素共面,然后证明这两个平面重合(此时也可用反证法)。
[本讲涉及的主要数学思想方法]
1、数学语言是数学表述和数学思维不可缺少的重要工具,必须能将这三种语言即文字语言、符号语言和图形语言进行准确的互译和表达,这在空间关系的证明与判断中显得十分重要;
2、空间观念和空间想象能力:高考中立体几何题的题型功能最重要的一点就是考查考生的空间观念和空间想象能力,因为我们是通过平面图形(直观图)去研究空间关系,所以同学们在学习过程中一定要多观察、多思考,动手做一些空间模型或通过电脑动画模拟一些空间图形,培养空间概念,提高空间想象能力。
【模拟试题】
一、选择题
1、在空间内,可以确定一个平面的条件是( )
A. 两两相交的三条直线
B. 三条直线,其中的一条与另两条分别相交
C. 三个点
D. 三条直线,它们两两相交,但不交于同一点
2、在正方体ABCDA1B1C1D1中,E、F分别为棱AA1、CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
A. 不存在 B. 有且只有两条 C. 有且只有三条 D. 有无数条
*3、已知平面外一点P和平面内不共线的三点A、B、C。A'、B'、C'分别在PA、PB、PC上,若延长A'B'、B'C'、A'C'与平面分别交于D、E、F三点,则D、E、F三点( )
A. 成钝角三角形 B. 成锐角三角形 C. 成直角三角形 D. 在一条直线上
4、空间中有三条线段AB、BC、CD,且∠ABC=∠BCD,那么直线AB与CD的位置关系是( )
A. 平行 B. 异面 C. 相交 D. 平行或异面或相交均有可能
5、下列叙述中正确的是( )
A. 因为P∈α,Q∈α,所以PQ∈α。
B. 因为P∈α,Q∈β,所以α∩β=PQ。
C. 因为,C∈AB,D∈AB,因此CD∈α。
D. 因为,所以A∈(α∩β)且B∈(α∩β)。
6、已知异面直线a,b分别在平面α,β内且α∩β=c,那么c( )
A. 至少与a,b中的一条相交;
B. 至多与a, b中的一条相交;
C. 至少与a,b中的一条平行;
D. 与a,b中的一条平行,与另一条相交
7、已知空间四边形ABCD中,M、N分别为AB、CD的中点,则下列判断正确的是( )
二、填空题
8、在空间四边形ABCD中,M、N分别是BC、AD的中点,则2MN与AB+CD的大小关系是 。
9、对于空间中的三条直线,有下列四个条件: 三条直线两两相交且不共点; 三条直线两两平行; 三条直线共点;④有两条直线平行,第三条直线和这两条直线都相交。其中,能推出三条直线共面的有 。
三、解答题
10、正方体ABCD-A1B1C1D1中,E、F分别是AB、AA1的中点。
求证:CE、D1F、DA三线共点;
求证:E、C、D1、F四点共面;
11、在正方体ABCD-A1B1C1D1中,若Q是A1C与平面ABC1D1的交点,求证:B、Q、D1三点共线。
12、如图,已知α∩β=a,bα,cβ,b∩a=A,c//a.求证:b与c是异面直线。
*13、正方体ABCD-A1B1C1D1中,P、Q、R分别是AB、AD、C1B1的中点,试作出正方体过P、Q、R三点的截面。
w.w.w.k.s.5.u.c.o.m
www.
一. 教学内容:
空间图形的基本关系与公理
二. 学习目标:
1、学会观察长方体模型中点、线、面之间的关系,并能结合长方体模型,掌握空间图形的有关概念和有关定理;掌握平面的基本性质、公理4和等角定理;
2、培养和发展自己的空间想象能力、运用图形语言进行交流的能力、几何直观能力、通过典型例子的学习和自主探索活动,理解数学概念和结论,体会蕴涵在其中的数学思想方法;
3、培养严谨的思维习惯与严肃的科学态度;体会推理论证中反映出的辩证思维的价值观。
三、知识要点
(一)空间位置关系:
I、空间点与线的关系
空间点与直线的位置关系有两种: 点P在直线上:; 点P在直线外:;
II、空间点与平面的关系
空间点与平面的位置关系有两种: 点P在平面上: 点P在平面外:;
III、空间直线与直线的位置关系:
IV、空间直线与平面的位置关系:
V、空间平面与平面的位置关系: 平行; 相交
说明:本模块中所说的“两个平面”“两条直线”等均指不重合的情形。
(二)异面直线的判定
1、定义法:采取反证法的思路,否定平行与相交两种情形即可;
2、判定定理:已知P点在平面上,则平面上不经过该点的直线与平面外经过该点的直线是异面直线。
(三)平面的基本性质公理
1、公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内(即直线在平面内,或曰平面经过这条直线)。
2、公理2 经过不在同一条直线上的三点,有且只有一个平面(即确定一个平面)。
3、公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条通过该点的公共直线。
4、平面的基本性质公理的三个推论
经过直线和直线外一点,有且只有一个平面;
经过两条相交直线,有且只有一个平面;
经过两条平行直线,有且只有一个平面
思考:
公理是公认为正确而不需要证明的命题,那么推论呢?
平面的基本性质公理是如何刻画平面的性质的?
(四)平行公理(公理4):平行于同一条直线的两条直线平行。
(五)等角定理:空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补。
(六)空间四边形:顺次连接不共面的四点构成的图形称为空间四边形。
【典型例题】
考点一 空间点线面位置关系的判断:主要判断依据是平面的基本性质公理及其推论,平行公理、等角定理等相关结论。
例1. 下列命题:
空间不同的三点可以确定一个平面;
有三个公共点的两个平面必定重合;
空间中两两相交的三条直线可以确定一个平面;
④平行四边形、梯形等所有的四边形都是平面图形;
⑤两组对边分别相等的四边形是平行四边形;
⑥一条直线和两平行线中的一条相交,必定和另一条也相交。
其中正确的命题是 。
解:⑥。
例2. 空间中三条直线可以确定几个平面?试画出示意图说明。
解:0个、1个、2个或3个。分别如图(图中所画平面为辅助平面):
考点二 异面直线的判断:主要依据是异面直线的定义及判定定理。
例3. 如图是一个正方体的展开图,如果将它还原为正方体,那么AB、CD、EF、GH这四条线段所在的直线是异面直线的有__________对,分别是____________________?
解:3对,分别是AB、GH;AB、CD;GH、EF。
考点三 “有且只有一个”的证明:一般地,此类题型的证明需要分为两个步骤,分别证明“有”即存在性和“只有一个”即唯一性。
例4. 求证:过两条平行直线有且只有一个平面。
已知:直线a∥b。
求证:过a,b有且只有一个平面。
证明: 存在性:由平行线的定义可知,过平行直线a,b有一个平面。
唯一性(反证法):假设过a,b有两个平面。在直线上任取两点A、B,在直线b上任取一点C,则A、B、C三点不共线。由于这两个平面都过直线a,b,因此由公理1可知:都过点A、B、C。由平面的基本性质公理2,过不共线三点的平面唯一存在,因此重合,与假设矛盾。矛盾表明:过平行直线a,b只有一个平面。
综上所述:过a,b有且只有一个平面。
考点四 共点的判断与证明:此类题型主要有三线共点和三面共点。
例5. 三个平面两两相交有三条交线,求证:三条交线或平行,或交于一点。
已知:平面,求证:a∥b∥c或者a,b,c交于一点P。
证明:因为,故a,b共面。
I、若a∥b:由于,故,因直线,故a,c无公共点。又a,c都在平面内,故a∥b;故a∥b∥c。
II、若,则,故知
综上所述:命题成立。
说明:证明三点共线的问题的常用思路是先证两条直线相交,然后再证该交点在第三条直线上;证明交点在第三条直线上常证明该点是两个相交平面的公共点,从而在这两个平面的交线上即在第三条直线上。
考点五 共线的判断与证明:常见题型是三点共线。
例6. 如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线。
证明:连结AC.因为A1C1∩B1D1=O1,B1D1平面B1D1A,A1C1AA1C1C,所以O1∈平面B1D1A且O1∈AA1C1C。同理可知,M∈平面B1D1A且M∈AA1C1C;A∈平面B1D1A且A∈AA1C1C。所以,O1、M、A三点在平面B1D1A和AA1C1C的交线上,故O1、M、A三点共线。
说明:证明三线共点问题的常见思路是证明第三点在前两点所确定的直线上;或者证明三点是两相交平面的公共点,从而在这两个平面的交线上。
考点六 共面问题的判断与证明:此类题型常见的是四点共面或三线共面,如证明某个图形是平面图形。
例7. 如图,在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且CG=BC/3,CH=DC/3。求证: E、F、G、H四点共面; 直线FH、EG、AC共点。
证明: 如图,连结HG,EF。在△ABD中,E、F分别为AB、AD中点,故EF是△ABD的中位线,故EF∥BD。在△CBD中,CG=BC/3,CH=DC/3,故GH∥BD,故EF∥GH,从而GH、EF可确定一个平面,即G、H、E、F四点共面。
由于E、F、G、H四点共面,且FH与EG不平行,故相交,记交点为M,则M∈FH,FH面ACD,故M∈面ACD;M∈EG,EG面ABC,故M∈面ABC。从而M是面ACD和面ABC的公共点,由公理3可知,M在这两个平面的交线AC上,从而FH、EG、AC三线共点。
说明:共面问题的常用的处理方法是利用平面的基本性质公理2及三个推论,先证明部分元素确定一个平面,再证剩下的元素也在此平面上;有时也可先证部分元素共面,剩下的元素共面,然后证明这两个平面重合(此时也可用反证法)。
[本讲涉及的主要数学思想方法]
1、数学语言是数学表述和数学思维不可缺少的重要工具,必须能将这三种语言即文字语言、符号语言和图形语言进行准确的互译和表达,这在空间关系的证明与判断中显得十分重要;
2、空间观念和空间想象能力:高考中立体几何题的题型功能最重要的一点就是考查考生的空间观念和空间想象能力,因为我们是通过平面图形(直观图)去研究空间关系,所以同学们在学习过程中一定要多观察、多思考,动手做一些空间模型或通过电脑动画模拟一些空间图形,培养空间概念,提高空间想象能力。
【模拟试题】
一、选择题
1、在空间内,可以确定一个平面的条件是( )
A. 两两相交的三条直线
B. 三条直线,其中的一条与另两条分别相交
C. 三个点
D. 三条直线,它们两两相交,但不交于同一点
2、在正方体ABCDA1B1C1D1中,E、F分别为棱AA1、CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
A. 不存在 B. 有且只有两条 C. 有且只有三条 D. 有无数条
*3、已知平面外一点P和平面内不共线的三点A、B、C。A'、B'、C'分别在PA、PB、PC上,若延长A'B'、B'C'、A'C'与平面分别交于D、E、F三点,则D、E、F三点( )
A. 成钝角三角形 B. 成锐角三角形 C. 成直角三角形 D. 在一条直线上
4、空间中有三条线段AB、BC、CD,且∠ABC=∠BCD,那么直线AB与CD的位置关系是( )
A. 平行 B. 异面 C. 相交 D. 平行或异面或相交均有可能
5、下列叙述中正确的是( )
A. 因为P∈α,Q∈α,所以PQ∈α。
B. 因为P∈α,Q∈β,所以α∩β=PQ。
C. 因为,C∈AB,D∈AB,因此CD∈α。
D. 因为,所以A∈(α∩β)且B∈(α∩β)。
6、已知异面直线a,b分别在平面α,β内且α∩β=c,那么c( )
A. 至少与a,b中的一条相交;
B. 至多与a, b中的一条相交;
C. 至少与a,b中的一条平行;
D. 与a,b中的一条平行,与另一条相交
7、已知空间四边形ABCD中,M、N分别为AB、CD的中点,则下列判断正确的是( )
二、填空题
8、在空间四边形ABCD中,M、N分别是BC、AD的中点,则2MN与AB+CD的大小关系是 。
9、对于空间中的三条直线,有下列四个条件: 三条直线两两相交且不共点; 三条直线两两平行; 三条直线共点;④有两条直线平行,第三条直线和这两条直线都相交。其中,能推出三条直线共面的有 。
三、解答题
10、正方体ABCD-A1B1C1D1中,E、F分别是AB、AA1的中点。
求证:CE、D1F、DA三线共点;
求证:E、C、D1、F四点共面;
11、在正方体ABCD-A1B1C1D1中,若Q是A1C与平面ABC1D1的交点,求证:B、Q、D1三点共线。
12、如图,已知α∩β=a,bα,cβ,b∩a=A,c//a.求证:b与c是异面直线。
*13、正方体ABCD-A1B1C1D1中,P、Q、R分别是AB、AD、C1B1的中点,试作出正方体过P、Q、R三点的截面。
w.w.w.k.s.5.u.c.o.m
www.
