直线的两点式方程
图片预览


文档简介
(共10张PPT)
复习:
(1)直线的点斜式方程:
(2)直线的斜截式方程:
注意:斜率存在
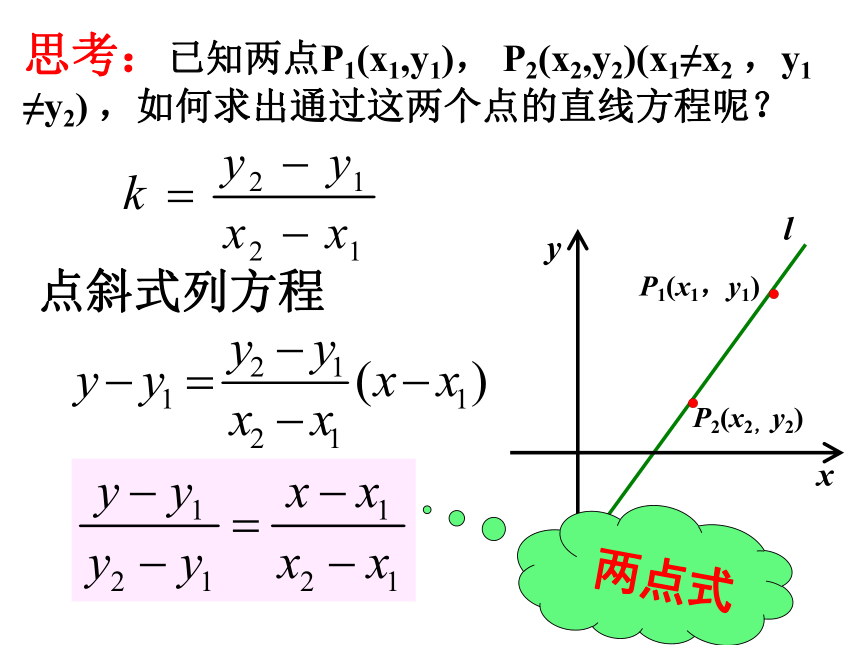
思考:已知两点P1(x1,y1), P2(x2,y2)(x1≠x2 ,y1 ≠y2) ,如何求出通过这两个点的直线方程呢?
x
y
l
P2(x2,y2)
P1(x1,y1)
点斜式列方程
两点式
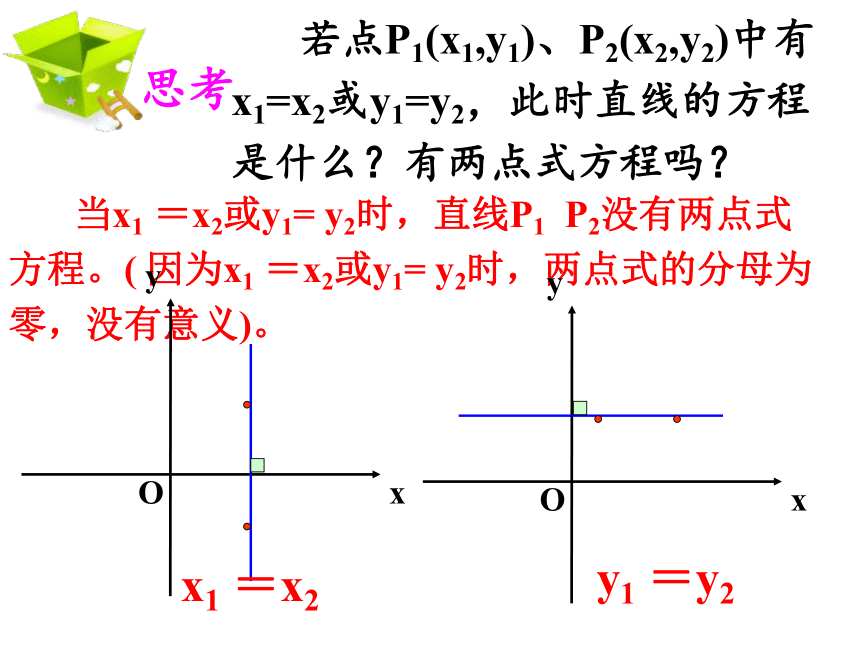
若点P1(x1,y1)、P2(x2,y2)中有x1=x2或y1=y2,此时直线的方程是什么?有两点式方程吗?
思考
当x1 =x2或y1= y2时,直线P1 P2没有两点式方程。( 因为x1 =x2或y1= y2时,两点式的分母为零,没有意义)。
x
O
y
x
O
y
x1 =x2
y1 =y2
x
y
l
A(a,0)
B(0,b)
横截距
纵截距
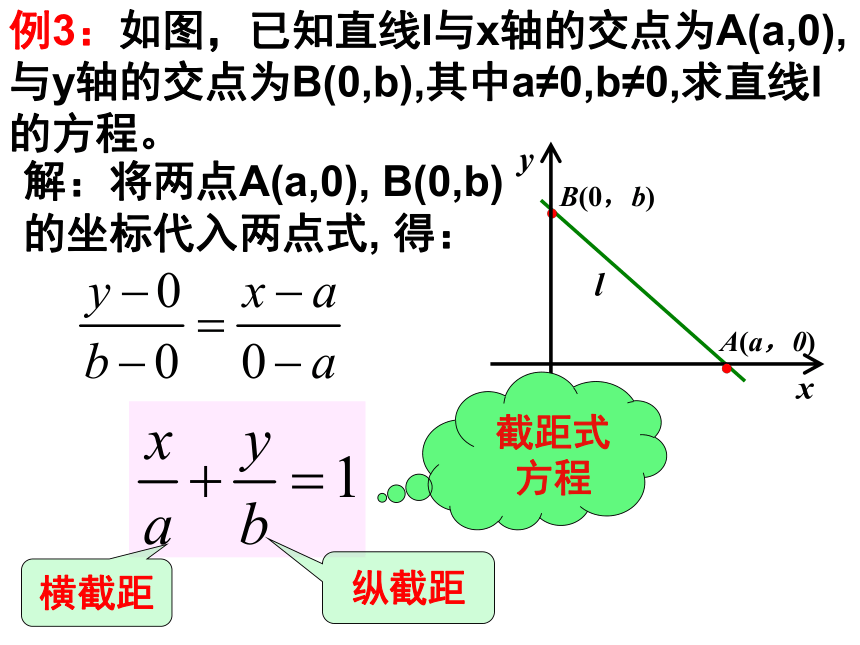
截距式方程
例3:如图,已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l的方程。
解:将两点A(a,0), B(0,b)
的坐标代入两点式, 得:
练习:求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程。
P
x
y
o
解:(1)若截距不为0, 设截距为a,则直线与x,y轴分别相交为(0,a),(a,0)则
将 P(-5,4)和k=-1代入点斜式方程 整理得 y =-x-1。
(2)若截距为0,则直线过点(0,0),将两个已知点带入两点式方程, 整理,得
例4 三角形的顶点是A(-5,0)B(3,-3)C(0,2)求BC、AC边所在两条直线的方程,以及BC边上中线所在直线的方程.
x
y
O
.
M
B
.
A
.
.
C
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
这就是BC边所在直线的方程。
BC边上的中线是顶点A与BC边中点M所连线段,由中点坐标公式可得点M的坐标为:
即
整理得:x+13y+5=0
这就是BC边上中线所在的直线的方程。
过A,M的直线方程
A
B
x
y
o
C
M
若A(x1,y1), B(x2,y2),求线段AB
垂直平分线的方程的步骤:
第一步:求线段AB中点坐标M( , )
x1+x2
2
y1+y2
2
第二步:求斜率
第三步:点斜式列方程
课堂小结
直线的两点式方程(x1≠x2 ,y1≠y2 )
直线的截距式方程(a≠0,b≠0)
复习:
(1)直线的点斜式方程:
(2)直线的斜截式方程:
注意:斜率存在
思考:已知两点P1(x1,y1), P2(x2,y2)(x1≠x2 ,y1 ≠y2) ,如何求出通过这两个点的直线方程呢?
x
y
l
P2(x2,y2)
P1(x1,y1)
点斜式列方程
两点式
若点P1(x1,y1)、P2(x2,y2)中有x1=x2或y1=y2,此时直线的方程是什么?有两点式方程吗?
思考
当x1 =x2或y1= y2时,直线P1 P2没有两点式方程。( 因为x1 =x2或y1= y2时,两点式的分母为零,没有意义)。
x
O
y
x
O
y
x1 =x2
y1 =y2
x
y
l
A(a,0)
B(0,b)
横截距
纵截距
截距式方程
例3:如图,已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l的方程。
解:将两点A(a,0), B(0,b)
的坐标代入两点式, 得:
练习:求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程。
P
x
y
o
解:(1)若截距不为0, 设截距为a,则直线与x,y轴分别相交为(0,a),(a,0)则
将 P(-5,4)和k=-1代入点斜式方程 整理得 y =-x-1。
(2)若截距为0,则直线过点(0,0),将两个已知点带入两点式方程, 整理,得
例4 三角形的顶点是A(-5,0)B(3,-3)C(0,2)求BC、AC边所在两条直线的方程,以及BC边上中线所在直线的方程.
x
y
O
.
M
B
.
A
.
.
C
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
这就是BC边所在直线的方程。
BC边上的中线是顶点A与BC边中点M所连线段,由中点坐标公式可得点M的坐标为:
即
整理得:x+13y+5=0
这就是BC边上中线所在的直线的方程。
过A,M的直线方程
A
B
x
y
o
C
M
若A(x1,y1), B(x2,y2),求线段AB
垂直平分线的方程的步骤:
第一步:求线段AB中点坐标M( , )
x1+x2
2
y1+y2
2
第二步:求斜率
第三步:点斜式列方程
课堂小结
直线的两点式方程(x1≠x2 ,y1≠y2 )
直线的截距式方程(a≠0,b≠0)
