人教版数学七年级下册 第5章 5.2平行线及其判定同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第5章 5.2平行线及其判定同步测试试题(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 158.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 11:48:06 | ||
图片预览


文档简介
平行线及其判定同步测试试题(一)
一.选择题
1.如图,下列条件中不能判定a∥b的是( )
A.∠1+∠4=180°
B.∠1=∠3
C.∠1=∠2
D.∠2=∠5
2.如图,已知∠1=∠2,其中能判定AB∥CD的是( )
A.
B.
C.
D.
3.如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
A.∠3=∠4
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
4.如图,在下列给出的条件下,不能判定AB∥DF的是( )
A.∠A+∠2=180°
B.∠A=∠3
C.∠1=∠4
D.∠1=∠A
5.如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )
A.若∠GAC=60°,则GH∥EF
B.若∠GAB=150°,则GH∥EF
C.若∠BAH=120°,则GH∥EF
D.若∠CAH=60°,则GH∥EF
6.如图,直线a,b被直线c所截,现给出下列四个条件:
①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.
其中能说明a∥b的条件序号为( )
A.①②
B.①③
C.①④
D.③④
7.平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
A.只有①
B.只有②
C.①②都正确
D.①②都不正确
8.如图,下列条件不能判定AB∥CD的是( )
A.∠1=∠2
B.∠3=∠4
C.∠B+∠BCD=180°
D.∠B=∠5
9.下列图形中,能由∠1=∠2得到AB∥CD的是( )
A.
B.
C.
D.
10.下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
A.
B.
C.
D.
二.填空题
11.若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是
.(工具不限,可结合图形进行说明,只要能说清思路即可)
12.下列说法中,①对顶角相等;②同位角相等;③过一点有且只有一条直线与已知直线垂直;④两点确定一条直线;⑤同旁内角互补,两直线平行;正确的有
(填序号)
13.如图,直角三角尺的直角顶点在直线b上,∠3=25°,转动直线a,当∠1=
时,a∥b.
14.如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件
或
,使EF∥AB.
15.如图,添加一个条件
,使AC∥DE.
三.解答题
16.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
17.(教材变式题)如图,已知B,E分别是线段AC,DF上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
18.(经典题)如图所示,完成下列填空.
(1)∵∠1=∠5(已知)
∴a∥
(同位角相等,两直线平行);
(2)∵∠3=
(已知)
∴a∥b(内错角相等,两直线平行);
(3)∵∠5+
=180°(已知)
∴
∥
(同旁内角互补,两直线平行).
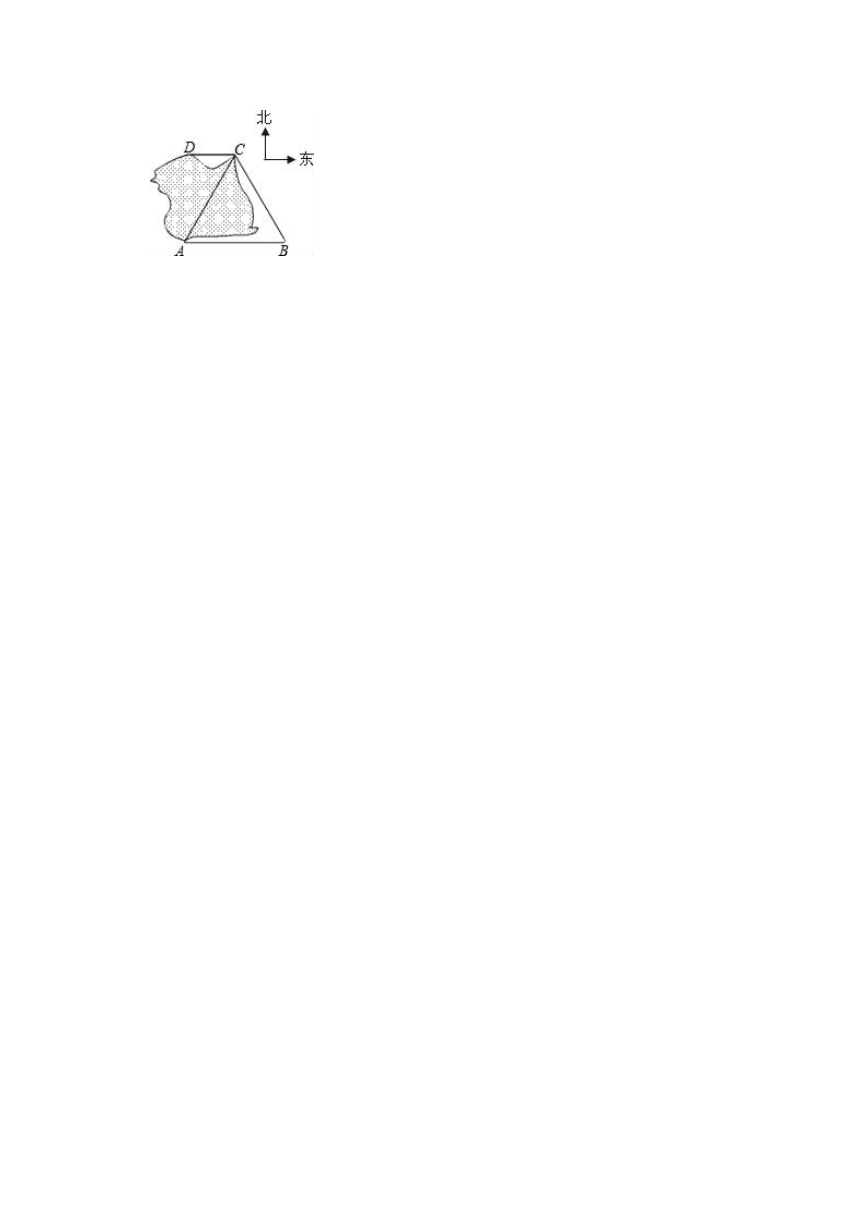
19.如图,某湖上风景区有两个观望点A,C和两个度假村B,D.度假村D在C正西方向,度假村B在C的南偏东30°方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A,B,C,D的位置,并求道路CD与CB的夹角;
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长;
(3)根据题目中的条件,能够判定DC∥AB吗?若能,请写出判断过程;若不能,请你加上一个条件,判定DC∥AB.
参考答案与试题解析
一.选择题
1.【解答】解:A、根据“邻补角互补”不可以判定a∥b,故本选项符合题意;
B、根据“内错角相等,两直线平行”可以判定a∥b,故本选项不符合题意;
C、根据“同位角相等,两直线平行”可以判定a∥b,故本选项不符合题意;
D、∵∠2=∠3,2=∠5,
∴∠3=∠5,
∴a∥b(同位角相等,两直线平行),故本选项不符合题意;
故选:A.
2.【解答】解:A、∵∠1=∠2,
∴AD∥BC(内错角相等,两直线平行);
B、∵∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
C、∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
D、∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选:D.
3.【解答】解:A、∵∠3=∠4,
∴BD∥AC,故本选项不合题意;
B、根据∠1=∠2不能推出BD∥AC,故本选项符合题意;
C、∵∠D=∠DCE,
∴BD∥AC,故本选项不合题意;
D、∵∠D+∠ACD=180°,
∴BD∥AC,故本选项不合题意;
故选:B.
4.【解答】解:A、∵∠A+∠2=180°,∴AB∥DF,故本选项错误;
B、∵∠A=∠3,∴AB∥DF,故本选项错误;
C、∵∠1=∠4,∴AB∥DF,故本选项错误;
D、∵∠1=∠A,∴AC∥DE,故本选项正确.
故选:D.
5.【解答】解:A、∵∠GAC=60°,∠EBA=60°,∴∠GAC=∠EBA,∴GH∥EF,故选项正确;
B、∵∠GAB=150°,∠EBA=60°,∴∠GAB+∠EBA=210°,∴GH与EF不平行,故选项错误;
C、∵∠BAH=120°,∠EBA=60°,∴∠HAB≠∠EBA,∴GH与EF不平行,故选项错误;
D、∵∠CAH=60°,∴∠GAB=60°,∵∠EBA=60°,∴∠GAB+∠EBA=120°,∴GH与EF不平行,故选项错误.
故选:A.
6.【解答】解:①∠1=∠5根据同位角相等两直线平行可得a∥b;
②∠1=∠7再由∠5=∠7可得∠1=∠5根据同位角相等两直线平行可得a∥b;
③∠2+∠3=180°不能判定a∥b;
④∠4=∠7不能判定a∥b.
故选:A.
7.【解答】解:①若a∥b,b∥c,则a∥c,说法正确;
②若a⊥b,b⊥c,则a⊥c,说法错误,应为同一平面内,若a⊥b,b⊥c,则a∥c;
故选:A.
8.【解答】解:A、∵∠1=∠2,∴AD∥BC,故本选项正确;
B、∵∠3=∠4,∴AB∥CD,故本选项错误;
C、∵∠B+∠BCD=180°,∴AB∥CD,故本选项错误;
D、∵∠B=∠5,∴AB∥CD,故本选项错误.
故选:A.
9.【解答】解:由∠1=∠2得到AB∥CD的是D选项,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴AB∥CD.
故选:D.
10.【解答】解:A、∠1和∠2的是对顶角,不能判断AB∥CD,此选项不正确;
B、∠1和∠2的对顶角是同位角,又相等,所以AB∥CD,此选项正确;
C、∠1和∠2的是内错角,又相等,故AD∥BC,不是AB∥CD,此选项错误;
D、∠1和∠2互为同旁内角,同旁内角相等两直线不平行,此选项错误.
故选:B.
二.填空题(共5小题)
11.【解答】解:根据同位角相等,两直线平行,可以画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.
故答案为:画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.
12.【解答】解:①对顶角相等,故正确;
②只有在两直线平行的条件下,同位角一定相等,故错误;
③在同一平面内,过一点有且只有一条直线与已知直线垂直,故错误;
④两点确定一条直线,故正确;
⑤同旁内角互补,两直线平行,正确;
故答案是:①④⑤.
13.【解答】解:∵直角三角尺的直角顶点在直线b上,∠3=25°,
∴∠2=90°﹣25°=65°,
∴当∠1=∠2=65°时,a∥b.
故答案为:65°.
14.【解答】解:当∠AEF=∠BAD时,EF∥AB,理由:内错角相等,两直线平行;
当∠CFE=∠BAC时,EF∥AB,理由:同位角相等,两直线平行;
故答案是:∠AEF=∠BAD或∠CFE=∠BAC(答案不唯一).
15.【解答】解:当∠BDE=∠A或∠BED=∠BCA或∠EDC=∠DCA或∠CED+∠ECA=180°即可判定.
故答案为∠BDE=∠A或∠BED=∠BCA或∠EDC=∠DCA或∠CED+∠ECA=180°.
三.解答题(共4小题)
16.【解答】解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
又∵∠5=∠6,
∴∠BAF=∠6,
∴AB∥CD,
∴∠2=∠EHA,
又∵∠1=∠2,即∠1=∠EHA,
∴BF∥DE.
另解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
∵∠5=∠6,
∴∠BAF=∠6,
∵△BFA、△DEC的内角和都是180°
∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6
∵∠1=∠2;∠BAF=∠6
∴∠BFA=∠4,
∴BF∥DE.
另解:BF、DE互相平行;
∵∠3=∠4,
∴BD∥CF,
∵∠2+∠3+∠6=180°(两直线平行,同旁内角互补),
∵∠1=∠2,∠5=∠6,
∴∠1+∠3+∠5=180°(等量代换),
∴BF∥DE(同旁内角互补,两直线平行).
17.【解答】证明:∵∠1=∠2,∠1=∠3(对顶角相等),
∴∠2=∠3,
∴BD∥EC,
∴∠DBC+∠C=180°(两直线平行,同旁内角互补);
又∵∠D=∠C,
∵∠DBC+∠D=180°,
∴DF∥AC(同旁内角互补,两直线平行).
18.【解答】解:(1)∵∠1=∠5,(已知)
∴a∥b(同位角相等,两直线平行);
(2)∵∠3=∠5,(已知)
∴a∥b(内错角相等,两直线平行);
(3)∵∠5+∠4=180°,(已知)
∴a∥b(同旁内角互补,两直线平行).
19.【解答】解:(1)如图所示,过C作CM⊥CD交AB与M,则∠DCM=90°,∠MCB=30°,
∴CD与CB的夹角为90°+30°=120°;
(2)环湖路的长=AB+BC﹣CD=3km;
(3)不能判定DC∥AB.
加上的条件可以是:∠B=60°.
证明:∵∠BCM=30°,∠B=60°,
∴∠CMB=90°,即CM⊥AB.
又∵CM⊥CD,
∴DC∥AB.
一.选择题
1.如图,下列条件中不能判定a∥b的是( )
A.∠1+∠4=180°
B.∠1=∠3
C.∠1=∠2
D.∠2=∠5
2.如图,已知∠1=∠2,其中能判定AB∥CD的是( )
A.
B.
C.
D.
3.如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
A.∠3=∠4
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
4.如图,在下列给出的条件下,不能判定AB∥DF的是( )
A.∠A+∠2=180°
B.∠A=∠3
C.∠1=∠4
D.∠1=∠A
5.如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )
A.若∠GAC=60°,则GH∥EF
B.若∠GAB=150°,则GH∥EF
C.若∠BAH=120°,则GH∥EF
D.若∠CAH=60°,则GH∥EF
6.如图,直线a,b被直线c所截,现给出下列四个条件:
①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.
其中能说明a∥b的条件序号为( )
A.①②
B.①③
C.①④
D.③④
7.平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
A.只有①
B.只有②
C.①②都正确
D.①②都不正确
8.如图,下列条件不能判定AB∥CD的是( )
A.∠1=∠2
B.∠3=∠4
C.∠B+∠BCD=180°
D.∠B=∠5
9.下列图形中,能由∠1=∠2得到AB∥CD的是( )
A.
B.
C.
D.
10.下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
A.
B.
C.
D.
二.填空题
11.若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是
.(工具不限,可结合图形进行说明,只要能说清思路即可)
12.下列说法中,①对顶角相等;②同位角相等;③过一点有且只有一条直线与已知直线垂直;④两点确定一条直线;⑤同旁内角互补,两直线平行;正确的有
(填序号)
13.如图,直角三角尺的直角顶点在直线b上,∠3=25°,转动直线a,当∠1=
时,a∥b.
14.如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件
或
,使EF∥AB.
15.如图,添加一个条件
,使AC∥DE.
三.解答题
16.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
17.(教材变式题)如图,已知B,E分别是线段AC,DF上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
18.(经典题)如图所示,完成下列填空.
(1)∵∠1=∠5(已知)
∴a∥
(同位角相等,两直线平行);
(2)∵∠3=
(已知)
∴a∥b(内错角相等,两直线平行);
(3)∵∠5+
=180°(已知)
∴
∥
(同旁内角互补,两直线平行).
19.如图,某湖上风景区有两个观望点A,C和两个度假村B,D.度假村D在C正西方向,度假村B在C的南偏东30°方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A,B,C,D的位置,并求道路CD与CB的夹角;
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长;
(3)根据题目中的条件,能够判定DC∥AB吗?若能,请写出判断过程;若不能,请你加上一个条件,判定DC∥AB.
参考答案与试题解析
一.选择题
1.【解答】解:A、根据“邻补角互补”不可以判定a∥b,故本选项符合题意;
B、根据“内错角相等,两直线平行”可以判定a∥b,故本选项不符合题意;
C、根据“同位角相等,两直线平行”可以判定a∥b,故本选项不符合题意;
D、∵∠2=∠3,2=∠5,
∴∠3=∠5,
∴a∥b(同位角相等,两直线平行),故本选项不符合题意;
故选:A.
2.【解答】解:A、∵∠1=∠2,
∴AD∥BC(内错角相等,两直线平行);
B、∵∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
C、∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
D、∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选:D.
3.【解答】解:A、∵∠3=∠4,
∴BD∥AC,故本选项不合题意;
B、根据∠1=∠2不能推出BD∥AC,故本选项符合题意;
C、∵∠D=∠DCE,
∴BD∥AC,故本选项不合题意;
D、∵∠D+∠ACD=180°,
∴BD∥AC,故本选项不合题意;
故选:B.
4.【解答】解:A、∵∠A+∠2=180°,∴AB∥DF,故本选项错误;
B、∵∠A=∠3,∴AB∥DF,故本选项错误;
C、∵∠1=∠4,∴AB∥DF,故本选项错误;
D、∵∠1=∠A,∴AC∥DE,故本选项正确.
故选:D.
5.【解答】解:A、∵∠GAC=60°,∠EBA=60°,∴∠GAC=∠EBA,∴GH∥EF,故选项正确;
B、∵∠GAB=150°,∠EBA=60°,∴∠GAB+∠EBA=210°,∴GH与EF不平行,故选项错误;
C、∵∠BAH=120°,∠EBA=60°,∴∠HAB≠∠EBA,∴GH与EF不平行,故选项错误;
D、∵∠CAH=60°,∴∠GAB=60°,∵∠EBA=60°,∴∠GAB+∠EBA=120°,∴GH与EF不平行,故选项错误.
故选:A.
6.【解答】解:①∠1=∠5根据同位角相等两直线平行可得a∥b;
②∠1=∠7再由∠5=∠7可得∠1=∠5根据同位角相等两直线平行可得a∥b;
③∠2+∠3=180°不能判定a∥b;
④∠4=∠7不能判定a∥b.
故选:A.
7.【解答】解:①若a∥b,b∥c,则a∥c,说法正确;
②若a⊥b,b⊥c,则a⊥c,说法错误,应为同一平面内,若a⊥b,b⊥c,则a∥c;
故选:A.
8.【解答】解:A、∵∠1=∠2,∴AD∥BC,故本选项正确;
B、∵∠3=∠4,∴AB∥CD,故本选项错误;
C、∵∠B+∠BCD=180°,∴AB∥CD,故本选项错误;
D、∵∠B=∠5,∴AB∥CD,故本选项错误.
故选:A.
9.【解答】解:由∠1=∠2得到AB∥CD的是D选项,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴AB∥CD.
故选:D.
10.【解答】解:A、∠1和∠2的是对顶角,不能判断AB∥CD,此选项不正确;
B、∠1和∠2的对顶角是同位角,又相等,所以AB∥CD,此选项正确;
C、∠1和∠2的是内错角,又相等,故AD∥BC,不是AB∥CD,此选项错误;
D、∠1和∠2互为同旁内角,同旁内角相等两直线不平行,此选项错误.
故选:B.
二.填空题(共5小题)
11.【解答】解:根据同位角相等,两直线平行,可以画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.
故答案为:画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.
12.【解答】解:①对顶角相等,故正确;
②只有在两直线平行的条件下,同位角一定相等,故错误;
③在同一平面内,过一点有且只有一条直线与已知直线垂直,故错误;
④两点确定一条直线,故正确;
⑤同旁内角互补,两直线平行,正确;
故答案是:①④⑤.
13.【解答】解:∵直角三角尺的直角顶点在直线b上,∠3=25°,
∴∠2=90°﹣25°=65°,
∴当∠1=∠2=65°时,a∥b.
故答案为:65°.
14.【解答】解:当∠AEF=∠BAD时,EF∥AB,理由:内错角相等,两直线平行;
当∠CFE=∠BAC时,EF∥AB,理由:同位角相等,两直线平行;
故答案是:∠AEF=∠BAD或∠CFE=∠BAC(答案不唯一).
15.【解答】解:当∠BDE=∠A或∠BED=∠BCA或∠EDC=∠DCA或∠CED+∠ECA=180°即可判定.
故答案为∠BDE=∠A或∠BED=∠BCA或∠EDC=∠DCA或∠CED+∠ECA=180°.
三.解答题(共4小题)
16.【解答】解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
又∵∠5=∠6,
∴∠BAF=∠6,
∴AB∥CD,
∴∠2=∠EHA,
又∵∠1=∠2,即∠1=∠EHA,
∴BF∥DE.
另解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
∵∠5=∠6,
∴∠BAF=∠6,
∵△BFA、△DEC的内角和都是180°
∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6
∵∠1=∠2;∠BAF=∠6
∴∠BFA=∠4,
∴BF∥DE.
另解:BF、DE互相平行;
∵∠3=∠4,
∴BD∥CF,
∵∠2+∠3+∠6=180°(两直线平行,同旁内角互补),
∵∠1=∠2,∠5=∠6,
∴∠1+∠3+∠5=180°(等量代换),
∴BF∥DE(同旁内角互补,两直线平行).
17.【解答】证明:∵∠1=∠2,∠1=∠3(对顶角相等),
∴∠2=∠3,
∴BD∥EC,
∴∠DBC+∠C=180°(两直线平行,同旁内角互补);
又∵∠D=∠C,
∵∠DBC+∠D=180°,
∴DF∥AC(同旁内角互补,两直线平行).
18.【解答】解:(1)∵∠1=∠5,(已知)
∴a∥b(同位角相等,两直线平行);
(2)∵∠3=∠5,(已知)
∴a∥b(内错角相等,两直线平行);
(3)∵∠5+∠4=180°,(已知)
∴a∥b(同旁内角互补,两直线平行).
19.【解答】解:(1)如图所示,过C作CM⊥CD交AB与M,则∠DCM=90°,∠MCB=30°,
∴CD与CB的夹角为90°+30°=120°;
(2)环湖路的长=AB+BC﹣CD=3km;
(3)不能判定DC∥AB.
加上的条件可以是:∠B=60°.
证明:∵∠BCM=30°,∠B=60°,
∴∠CMB=90°,即CM⊥AB.
又∵CM⊥CD,
∴DC∥AB.
