人教版数学七年级下册5.1.1 相交线学案(无答案)
文档属性
| 名称 | 人教版数学七年级下册5.1.1 相交线学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览

文档简介
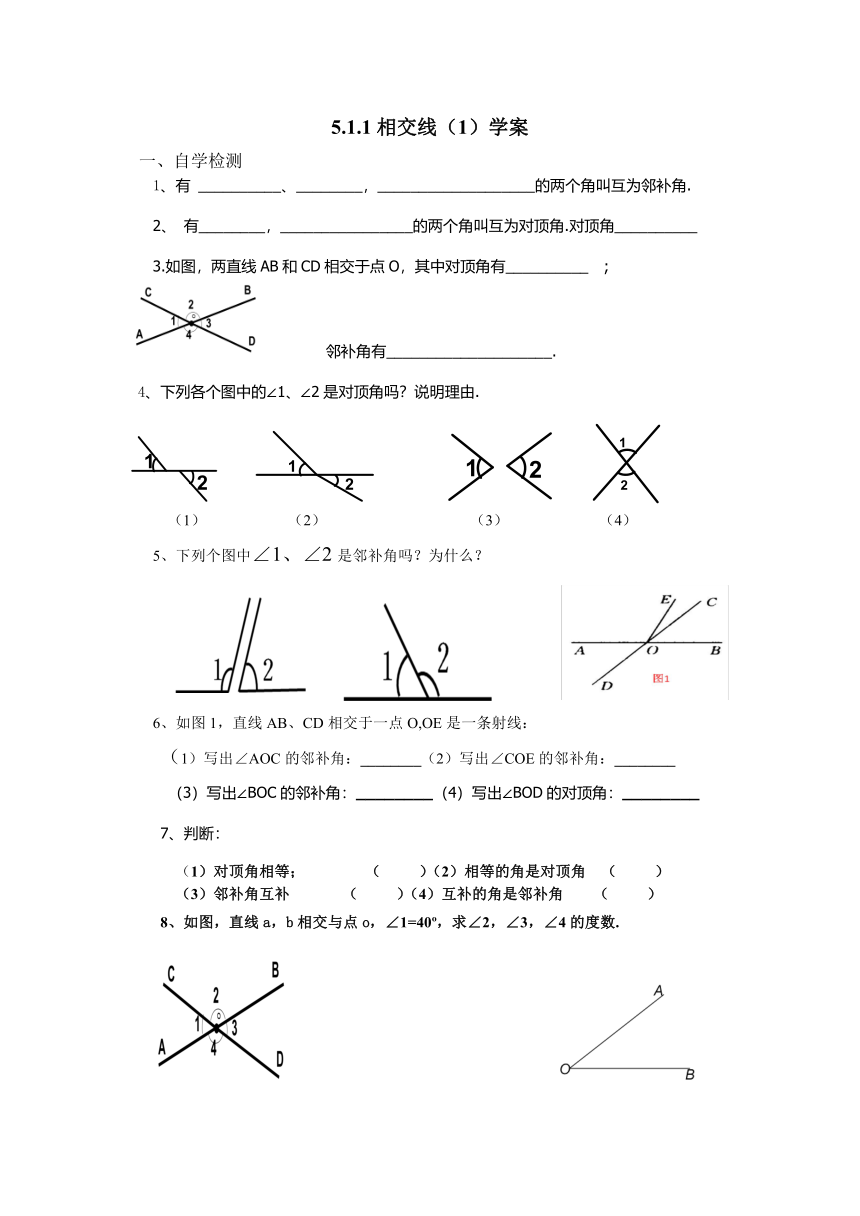
5.1.1相交线(1)学案
一、自学检测
1、有
__________、________,___________________的两个角叫互为邻补角.
2、
有________,________________的两个角叫互为对顶角.对顶角__________
3.如图,两直线AB和CD相交于点O,其中对顶角有__________
;
邻补角有____________________.
4、下列各个图中的∠1、∠2是对顶角吗?说明理由.
(2)
(3)
(4)
5、下列个图中∠1、∠2是邻补角吗?为什么?
6、如图1,直线AB、CD相交于一点O,OE是一条射线:
(1)写出∠AOC的邻补角:________(2)写出∠COE的邻补角:________
(3)写出∠BOC的邻补角:________(4)写出∠BOD的对顶角:________
7、判断:
(1)对顶角相等;
(
)(2)相等的角是对顶角
(
)
(3)邻补角互补
(
)(4)互补的角是邻补角
(
)
8、如图,直线a,b相交与点o,∠1=40?,求∠2,∠3,∠4的度数.
二、交流展示:
1、如上图,画出∠AOB的邻补角和对顶角。
2、如图,你是怎样得到∠2=∠4的?与∠2,∠4的大小有关系吗?
结论是什么?
3、如图,直线AB、CD相交于O,∠AOC=70°,∠1=30°.求∠2的度数.
三、总结提升
本节课你有什么收获?分享给大家.
四、效果检测
1、如图是一把剪刀,其中∠1=40°,则∠2=__________,
2、如图,当剪子∠AOB增大15°时,∠COD增大_______度,其根据是_______.
3、已知∠1与∠2为对顶角,且∠1的补角的度数为80°,则∠2的度数为 °
4、一个角的对顶角有
个,邻补角有
个,补角有
个.
5、完成推理过程。
如上图,因为∠1+∠2
=
,∠2+∠3
=
。(邻补角定义)
所以∠1=180°-
,∠3
=180°-
(等式性质)
所以
=
由上面推理可知,对顶角的性质:对顶角
。
6、如图,已知直线AB,CD,EF相交于点o,∠AOC=40,°∠BOF=65°,则∠DOE=
°.
7、直线AB、CD交于点O,OE是∠AOD的平分线,已知∠AOC=50°.
求∠BOE的度数.
一、自学检测
1、有
__________、________,___________________的两个角叫互为邻补角.
2、
有________,________________的两个角叫互为对顶角.对顶角__________
3.如图,两直线AB和CD相交于点O,其中对顶角有__________
;
邻补角有____________________.
4、下列各个图中的∠1、∠2是对顶角吗?说明理由.
(2)
(3)
(4)
5、下列个图中∠1、∠2是邻补角吗?为什么?
6、如图1,直线AB、CD相交于一点O,OE是一条射线:
(1)写出∠AOC的邻补角:________(2)写出∠COE的邻补角:________
(3)写出∠BOC的邻补角:________(4)写出∠BOD的对顶角:________
7、判断:
(1)对顶角相等;
(
)(2)相等的角是对顶角
(
)
(3)邻补角互补
(
)(4)互补的角是邻补角
(
)
8、如图,直线a,b相交与点o,∠1=40?,求∠2,∠3,∠4的度数.
二、交流展示:
1、如上图,画出∠AOB的邻补角和对顶角。
2、如图,你是怎样得到∠2=∠4的?与∠2,∠4的大小有关系吗?
结论是什么?
3、如图,直线AB、CD相交于O,∠AOC=70°,∠1=30°.求∠2的度数.
三、总结提升
本节课你有什么收获?分享给大家.
四、效果检测
1、如图是一把剪刀,其中∠1=40°,则∠2=__________,
2、如图,当剪子∠AOB增大15°时,∠COD增大_______度,其根据是_______.
3、已知∠1与∠2为对顶角,且∠1的补角的度数为80°,则∠2的度数为 °
4、一个角的对顶角有
个,邻补角有
个,补角有
个.
5、完成推理过程。
如上图,因为∠1+∠2
=
,∠2+∠3
=
。(邻补角定义)
所以∠1=180°-
,∠3
=180°-
(等式性质)
所以
=
由上面推理可知,对顶角的性质:对顶角
。
6、如图,已知直线AB,CD,EF相交于点o,∠AOC=40,°∠BOF=65°,则∠DOE=
°.
7、直线AB、CD交于点O,OE是∠AOD的平分线,已知∠AOC=50°.
求∠BOE的度数.
