3.2.1双曲线及其标准方程 课件-2021年秋高中数学人教版(2019)选择性必修一(45张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程 课件-2021年秋高中数学人教版(2019)选择性必修一(45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 21:43:46 | ||
图片预览




文档简介
3.2.1 双曲线及其标准方程
高二年级 数学
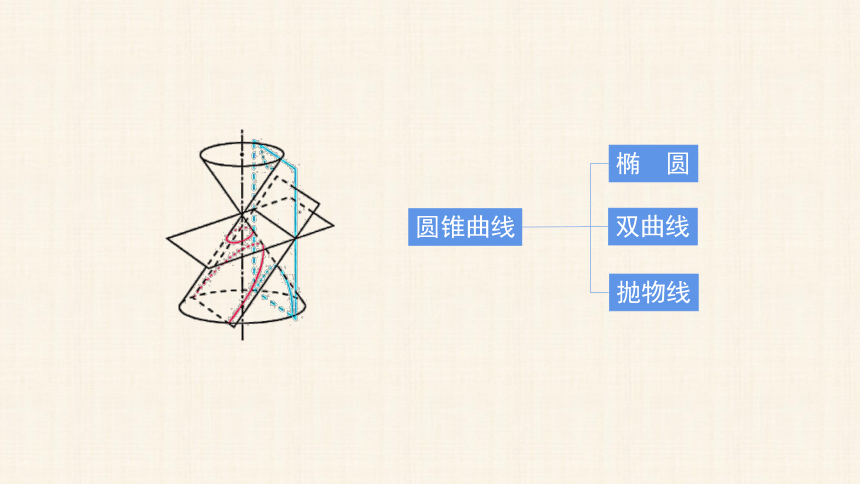
圆锥曲线
椭 圆
双曲线
抛物线
焦点在 y 轴上的椭圆标准方程:
焦点在 x 轴上的椭圆标准方程:
一、复习引入
椭圆:平面内与两个定点F1,F2的距离的和等于常数 (大于|F1F2|)的点的轨迹.
设点
建系
列式
化简、检验.
平面内与两个定点F1,F2的距离的和等于常数 (大于|F1F2|)的点的轨迹叫做椭圆.
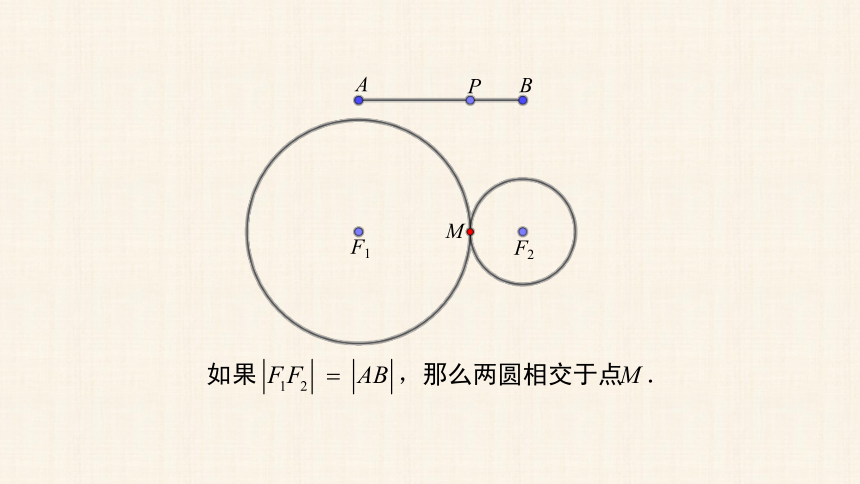
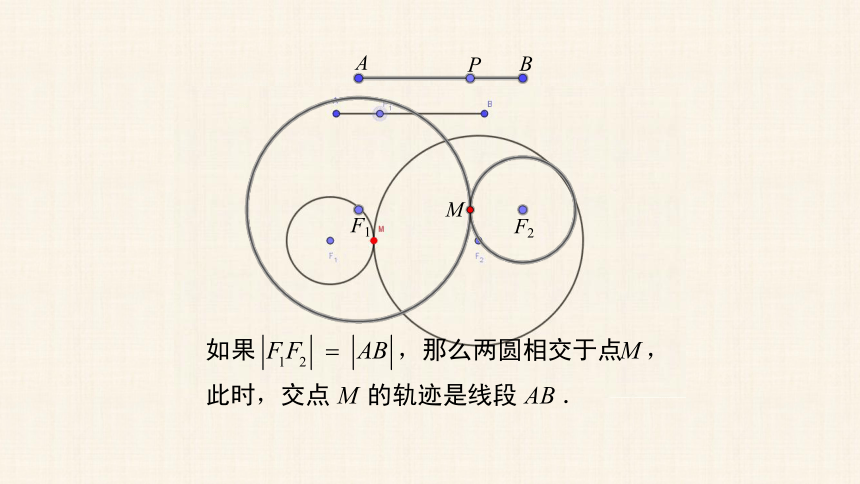
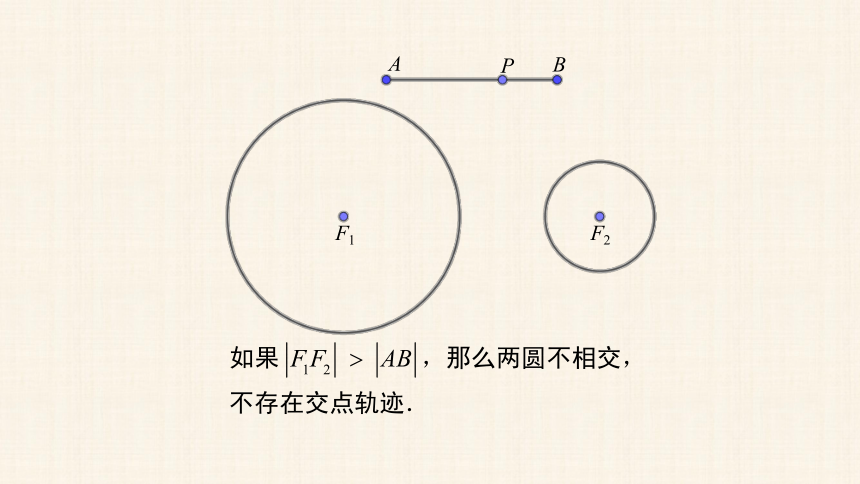
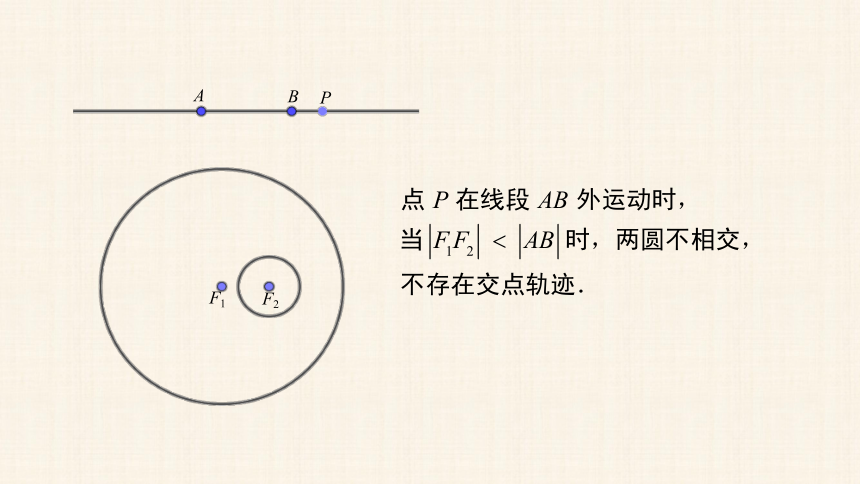
平面内与两个定点的距离的差等于常数的点的轨迹是什么?
思考
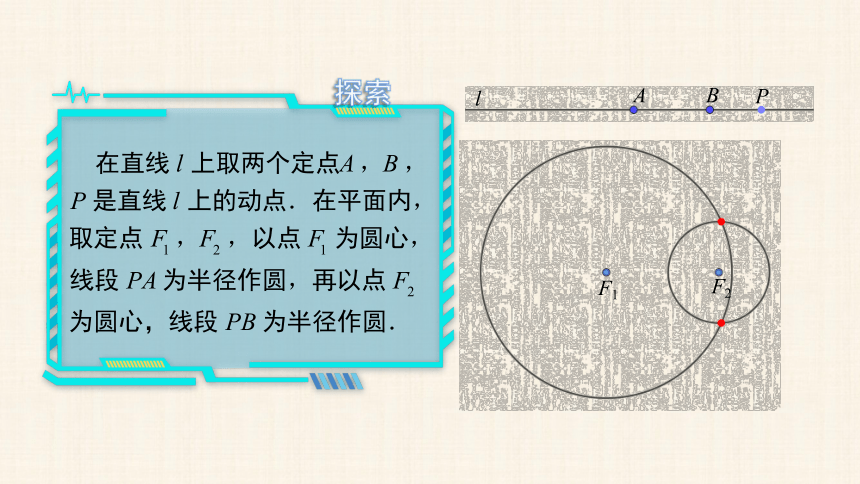
探索
A
B
P
l
F1
F2
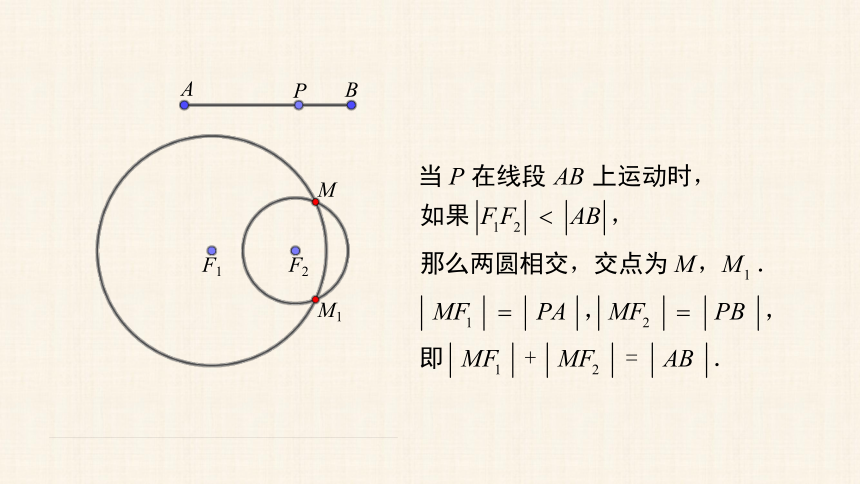
A
B
P
F1
F2
M
M1
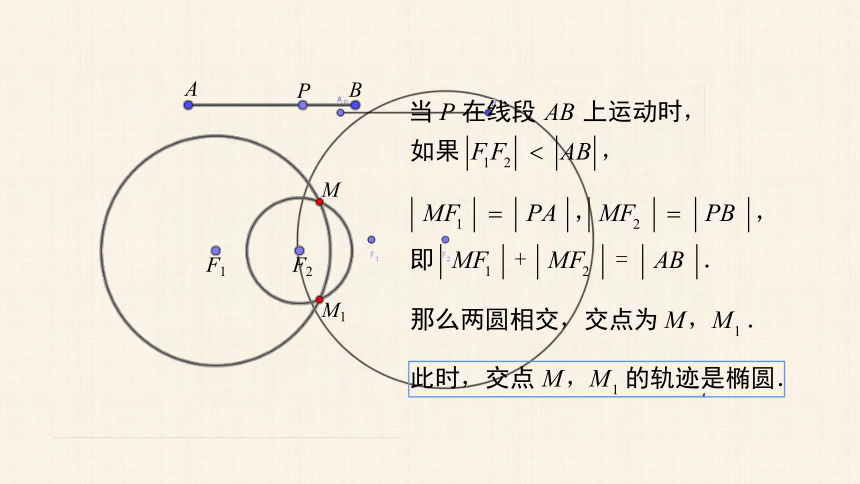
A
B
P
F1
F2
M
M1
A
B
P
F1
F2
M
A
B
P
F1
F2
M
A
B
P
F1
F2
A
B
P
F1
F2
A
B
P
F1
F2
M
A
B
P
F1
F2
M
A
B
P
F1
F2
M
M1
A
B
P
F1
F2
M
M1
(B )
A
P
F1
F2
M
M1
二、新知探究
我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
F1
F2
M
x
y
O
类比求椭圆标准方程的过程,我们如何建立适当的坐标系,得出双曲线的方程?
探索:
F1
F2
x
y
O
F1
F2
x
y
O
双曲线标准方程的推导
建立如图所示的平面直角坐标系Oxy.
设 M ( x ,y )是双曲线上任意一点,
双曲线的焦距为 2c( c > 0),
则有F1( -c,0),F2 ( c,0).
又设||MF1|-|MF2||= 2a( a 为大于 0 的常数).
由双曲线的定义,双曲线就是下列点的集合:
①
两边平方,整理得:
双曲线上任意一点的坐标(x,y)都是方程②的解;
以方程②的解为坐标的点(x,y)与双曲线的两个焦点F1(-c,0),F2(c,0)的距离之差的绝对值都为2a,
②
即以方程②的解为坐标的点都在双曲线上.
我们称方程②是双曲线的方程,这个方程叫做双曲线的标准方程.
它表示焦点在 x 轴上,两个焦点分别是 F1(- c,0),F2(c,0) 的双曲线,
这里 .
②
思考
如图,双曲线的焦距为 2c ,焦点分别是
F1(0 ,-c),F2(0 ,c).a ,b 的意义同上,
这时双曲线的方程是
焦点在 y 轴上的双曲线标准方程:
焦点在 x 轴上的双曲线标准方程:
观察双曲线标准方程的特点:
1.两个焦点位置(在 x 轴还是在 y 轴)与负号的关系;
2.方程中 x, y 与 a,b 的对应位置.
{D7AC3CCA-C797-4891-BE02-D94E43425B78}椭圆及其标准方程
双曲线及其标准方程
三、典例解析
探索
如图设 A,B 两点的坐标分别为(-5,0),(5,0),直线 AM,BM 相交于点 M,且它们的斜率之积是 ,试求点M 的轨迹方程,并由点 M 的轨迹方程判断轨迹的形状,与3.1 例 3 比较,你有什么发现?
分析:设点 M 的坐标为(x ,y),那么直线 AM,BM 的斜率就可用含 x,y 的关系式分别表示.由直线 AM,BM的斜率之积是 ,可得出 x,y 之间的关系式,进而得到点 M 的轨迹方程.
解:设点M 的坐标为(x,y),因为点A的坐标为(- 5,0), 所以直线 AM 的斜率
由已知,有
同理,直线 BM 的斜率
所以点M 的轨迹是除去(-5,0),(5,0)两点的双曲线.
化简,得点M 的轨迹方程为
练习
归
纳
总
结
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
四、课后作业
(1)教材P121练习 2,3,4 .
(2)教材P127习题3.2 1,2 .
感 谢 聆 听
高二年级 数学
圆锥曲线
椭 圆
双曲线
抛物线
焦点在 y 轴上的椭圆标准方程:
焦点在 x 轴上的椭圆标准方程:
一、复习引入
椭圆:平面内与两个定点F1,F2的距离的和等于常数 (大于|F1F2|)的点的轨迹.
设点
建系
列式
化简、检验.
平面内与两个定点F1,F2的距离的和等于常数 (大于|F1F2|)的点的轨迹叫做椭圆.
平面内与两个定点的距离的差等于常数的点的轨迹是什么?
思考
探索
A
B
P
l
F1
F2
A
B
P
F1
F2
M
M1
A
B
P
F1
F2
M
M1
A
B
P
F1
F2
M
A
B
P
F1
F2
M
A
B
P
F1
F2
A
B
P
F1
F2
A
B
P
F1
F2
M
A
B
P
F1
F2
M
A
B
P
F1
F2
M
M1
A
B
P
F1
F2
M
M1
(B )
A
P
F1
F2
M
M1
二、新知探究
我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
F1
F2
M
x
y
O
类比求椭圆标准方程的过程,我们如何建立适当的坐标系,得出双曲线的方程?
探索:
F1
F2
x
y
O
F1
F2
x
y
O
双曲线标准方程的推导
建立如图所示的平面直角坐标系Oxy.
设 M ( x ,y )是双曲线上任意一点,
双曲线的焦距为 2c( c > 0),
则有F1( -c,0),F2 ( c,0).
又设||MF1|-|MF2||= 2a( a 为大于 0 的常数).
由双曲线的定义,双曲线就是下列点的集合:
①
两边平方,整理得:
双曲线上任意一点的坐标(x,y)都是方程②的解;
以方程②的解为坐标的点(x,y)与双曲线的两个焦点F1(-c,0),F2(c,0)的距离之差的绝对值都为2a,
②
即以方程②的解为坐标的点都在双曲线上.
我们称方程②是双曲线的方程,这个方程叫做双曲线的标准方程.
它表示焦点在 x 轴上,两个焦点分别是 F1(- c,0),F2(c,0) 的双曲线,
这里 .
②
思考
如图,双曲线的焦距为 2c ,焦点分别是
F1(0 ,-c),F2(0 ,c).a ,b 的意义同上,
这时双曲线的方程是
焦点在 y 轴上的双曲线标准方程:
焦点在 x 轴上的双曲线标准方程:
观察双曲线标准方程的特点:
1.两个焦点位置(在 x 轴还是在 y 轴)与负号的关系;
2.方程中 x, y 与 a,b 的对应位置.
{D7AC3CCA-C797-4891-BE02-D94E43425B78}椭圆及其标准方程
双曲线及其标准方程
三、典例解析
探索
如图设 A,B 两点的坐标分别为(-5,0),(5,0),直线 AM,BM 相交于点 M,且它们的斜率之积是 ,试求点M 的轨迹方程,并由点 M 的轨迹方程判断轨迹的形状,与3.1 例 3 比较,你有什么发现?
分析:设点 M 的坐标为(x ,y),那么直线 AM,BM 的斜率就可用含 x,y 的关系式分别表示.由直线 AM,BM的斜率之积是 ,可得出 x,y 之间的关系式,进而得到点 M 的轨迹方程.
解:设点M 的坐标为(x,y),因为点A的坐标为(- 5,0), 所以直线 AM 的斜率
由已知,有
同理,直线 BM 的斜率
所以点M 的轨迹是除去(-5,0),(5,0)两点的双曲线.
化简,得点M 的轨迹方程为
练习
归
纳
总
结
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
四、课后作业
(1)教材P121练习 2,3,4 .
(2)教材P127习题3.2 1,2 .
感 谢 聆 听
