2.3.4两条平行直线间的距离 课件-2020年秋高中数学人教版(2019)选择性必修一(22张PPT)
文档属性
| 名称 | 2.3.4两条平行直线间的距离 课件-2020年秋高中数学人教版(2019)选择性必修一(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 600.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览







文档简介
2.3.4 两条平行直线间的距离
高二年级 数学
一、复习回顾
问题:如何求两条平行直线间的距离呢?
两点间的距离公式 已知平面内两点 ,
则
点到直线的距离公式 点 到直线 的距离
两条平行直线间的距离是指夹在这两条平行直线
间的公垂线段的长.
二、探究新知
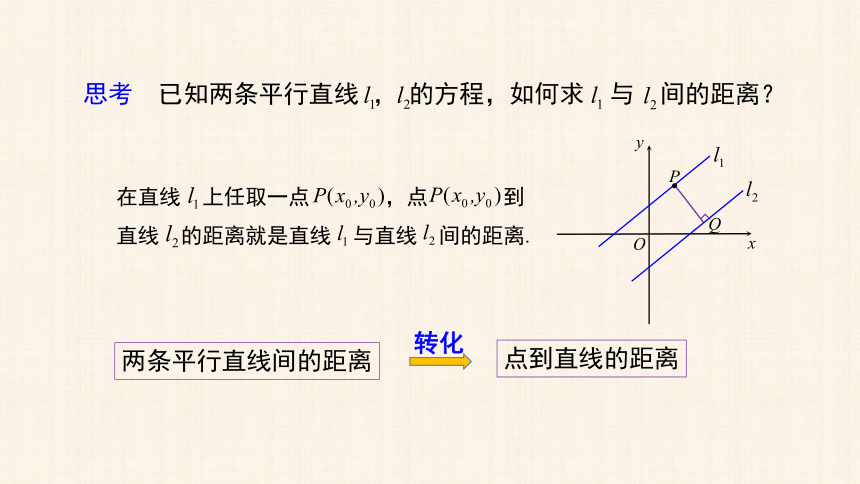
思考 已知两条平行直线 的方程,如何求 与 间的距离?
两条平行直线间的距离
点到直线的距离
转化
在直线 上任取一点 ,点 到直线 的距离就是直线 与直线 间的距离.
三、典型例题
例1 已知两条平行直线 , ,
求 与 间的距离.
分析:在 上选取一点,如 与坐标轴的交点,用点到直线的距离公式求这点到 的距离,即 与 间的距离.
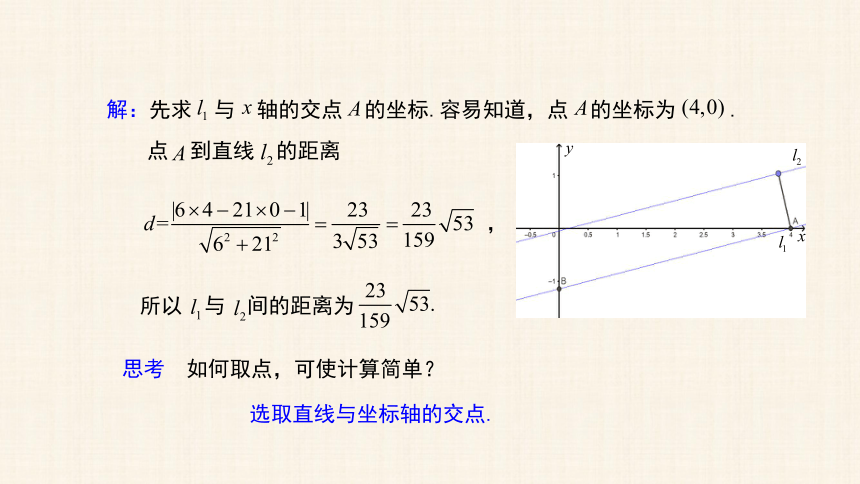
解:先求 与 轴的交点 的坐标.容易知道,点 的坐标为 .
点 到直线 的距离
所以 与 间的距离为
思考 如何取点,可使计算简单?
选取直线与坐标轴的交点.
分析:两条平行直线间的距离即为这两条平行直线中的一条直线上的一点到另一条直线的距离.
例2 求证:两条平行直线 与 间的距离为
证明:在直线 上任取一点 ,点 到
直线 的距离就是这两条平行直线间的距离,即
因为点 在直线 上,所以 ,即 ,因此
结论:两条平行直线 与 间的距离为
注意:两条平行直线的方程中 的系数对应相等.
例1 已知两条平行直线 , ,
求 与 间的距离.
另解:直线 的方程可以化为 ,
因为 ,
于是
所以 与 间的距离为
1. 求下列两条平行直线间的距离:
四、课堂练习
(1) , ;
解:先求 与 轴的交点 的坐标为 .
点 到直线 的距离
所以 与 间的距离为
另解:
所以 与 间的距离为
1. 求下列两条平行直线间的距离:
四、课堂练习
(2) , .
提示: .
解:
2. 已知两条平行直线 与 间的
距离为3,求 的值.
解:因为 ,
所以 或
3. 求两条平行直线 与 间的距离.
解:因为直线 与直线 平行,
所以 将 化为 ,
得到
4. 如图,已知直线 与直线 ,在 上任取一点 ,在 上任取一点 ,连接 ,取 的靠近点 的三等分点 ,过 作 的平行线 ,求 与 间的距离.
解:过点 作 的垂线分别与 和 交于 ,
因为 互相平行,所以 ,
于是 即为 与 间的距离.
因为 ,所以 .
因为 , ,
从而
所以
即 与 间的距离为
5. ? 的四条边所在直线的方程分别是
,求? 的面积.
解:解方程组 及
得
所以 与 相交,交点 ,
与 相交,交点 ,
于是
因为 ,所以 与 的距离为
从而 ,
所以
设边 上的高为 ,
五、总结提升
两条平行直线间的距离
1.两条平行直线间的距离可以转化为其中一条直线上的一点到另一条直
线的距离.
2.两条平行直线 与 间的距离为 .
3.体会化归与转化的数学思想.
距离
公式
两点
,
?
点到直线
,
?
两条平行直线
?
教科书第79页习题2.3第7,8题
六、布置作业
谢 谢!
高二年级 数学
一、复习回顾
问题:如何求两条平行直线间的距离呢?
两点间的距离公式 已知平面内两点 ,
则
点到直线的距离公式 点 到直线 的距离
两条平行直线间的距离是指夹在这两条平行直线
间的公垂线段的长.
二、探究新知
思考 已知两条平行直线 的方程,如何求 与 间的距离?
两条平行直线间的距离
点到直线的距离
转化
在直线 上任取一点 ,点 到直线 的距离就是直线 与直线 间的距离.
三、典型例题
例1 已知两条平行直线 , ,
求 与 间的距离.
分析:在 上选取一点,如 与坐标轴的交点,用点到直线的距离公式求这点到 的距离,即 与 间的距离.
解:先求 与 轴的交点 的坐标.容易知道,点 的坐标为 .
点 到直线 的距离
所以 与 间的距离为
思考 如何取点,可使计算简单?
选取直线与坐标轴的交点.
分析:两条平行直线间的距离即为这两条平行直线中的一条直线上的一点到另一条直线的距离.
例2 求证:两条平行直线 与 间的距离为
证明:在直线 上任取一点 ,点 到
直线 的距离就是这两条平行直线间的距离,即
因为点 在直线 上,所以 ,即 ,因此
结论:两条平行直线 与 间的距离为
注意:两条平行直线的方程中 的系数对应相等.
例1 已知两条平行直线 , ,
求 与 间的距离.
另解:直线 的方程可以化为 ,
因为 ,
于是
所以 与 间的距离为
1. 求下列两条平行直线间的距离:
四、课堂练习
(1) , ;
解:先求 与 轴的交点 的坐标为 .
点 到直线 的距离
所以 与 间的距离为
另解:
所以 与 间的距离为
1. 求下列两条平行直线间的距离:
四、课堂练习
(2) , .
提示: .
解:
2. 已知两条平行直线 与 间的
距离为3,求 的值.
解:因为 ,
所以 或
3. 求两条平行直线 与 间的距离.
解:因为直线 与直线 平行,
所以 将 化为 ,
得到
4. 如图,已知直线 与直线 ,在 上任取一点 ,在 上任取一点 ,连接 ,取 的靠近点 的三等分点 ,过 作 的平行线 ,求 与 间的距离.
解:过点 作 的垂线分别与 和 交于 ,
因为 互相平行,所以 ,
于是 即为 与 间的距离.
因为 ,所以 .
因为 , ,
从而
所以
即 与 间的距离为
5. ? 的四条边所在直线的方程分别是
,求? 的面积.
解:解方程组 及
得
所以 与 相交,交点 ,
与 相交,交点 ,
于是
因为 ,所以 与 的距离为
从而 ,
所以
设边 上的高为 ,
五、总结提升
两条平行直线间的距离
1.两条平行直线间的距离可以转化为其中一条直线上的一点到另一条直
线的距离.
2.两条平行直线 与 间的距离为 .
3.体会化归与转化的数学思想.
距离
公式
两点
,
?
点到直线
,
?
两条平行直线
?
教科书第79页习题2.3第7,8题
六、布置作业
谢 谢!
