2020—2021学年人教版八年级下册 第17章 勾股定理 复习课课件(19张)
文档属性
| 名称 | 2020—2021学年人教版八年级下册 第17章 勾股定理 复习课课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 296.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 00:34:08 | ||
图片预览



文档简介
17章 勾股定理复习课
互逆定理
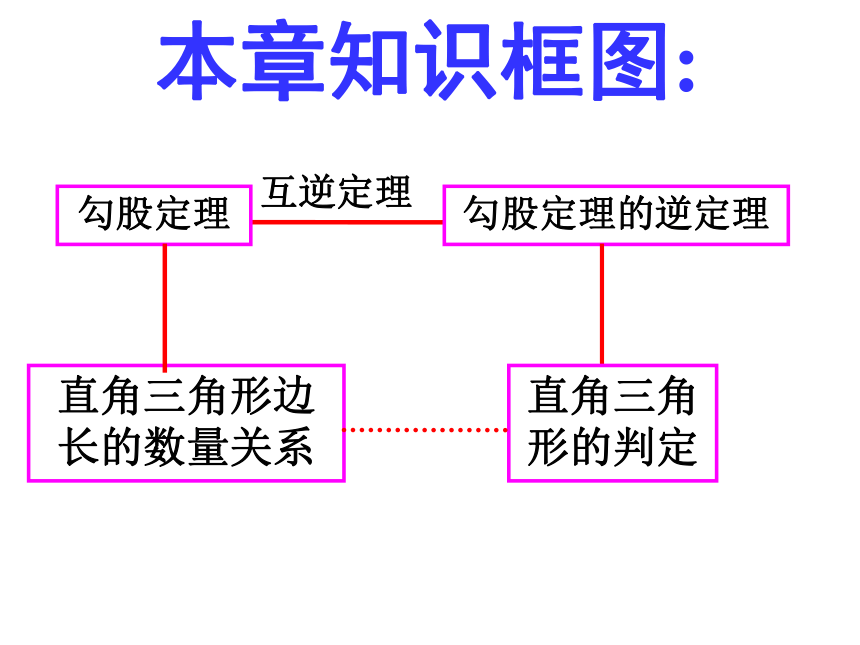
本章知识框图:
勾股定理
勾股定理的逆定理
直角三角形的判定
直角三角形边长的数量关系
1.勾股定理
直角三角形两直角边a、 b的平方和,等于斜边c的平方。
2.勾股定理的逆定理
如果三角形三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股数.
熟记常见的勾股数(如3、4、5)
3.勾股数
4.互逆命题与互逆定理的概念
勾股定理
勾股定理的逆定理
题设
在Rt△ABC 中,∠C=900
在△ABC 中, 三边a,b,c满足a2+b2=c2
结论
a2+b2=c2
∠C=900
作用
1.用勾股定理进行计算
2.证明与平方有关的问题3.解决实际问题
1.判断某三角形是否为直角三角形(3种)
2.解决实际问题
联系
1.两个定理都与“三角形的三边关系a2+b2=c2”有关;
2.都与直角三角形有关;
3.都是数形结合思想的体现。
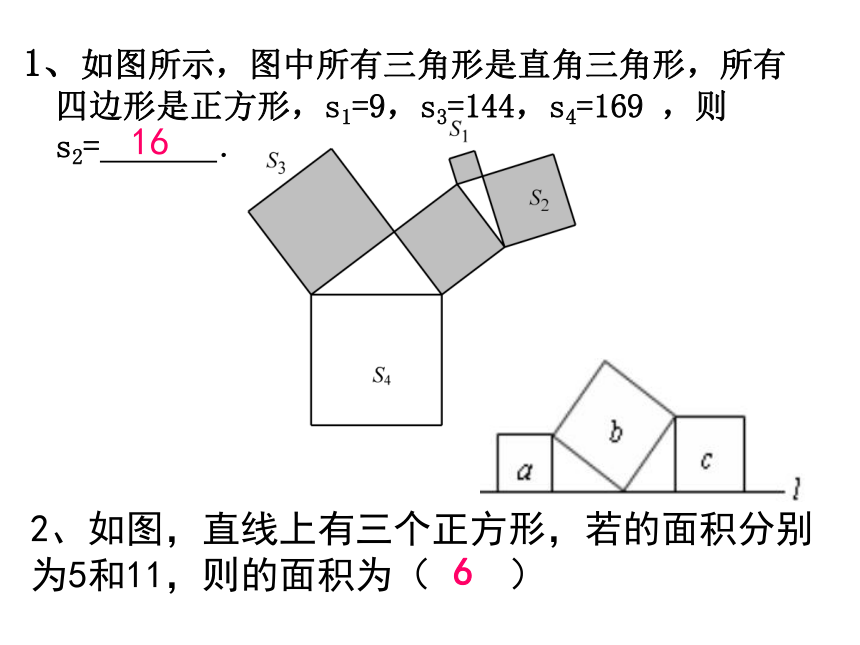
1、如图所示,图中所有三角形是直角三角形,所有四边形是正方形,s1=9,s3=144,s4=169 ,则s2= .
16
2、如图,直线上有三个正方形,若的面积分别为5和11,则的面积为( )
6
D
A
C
B
1
2
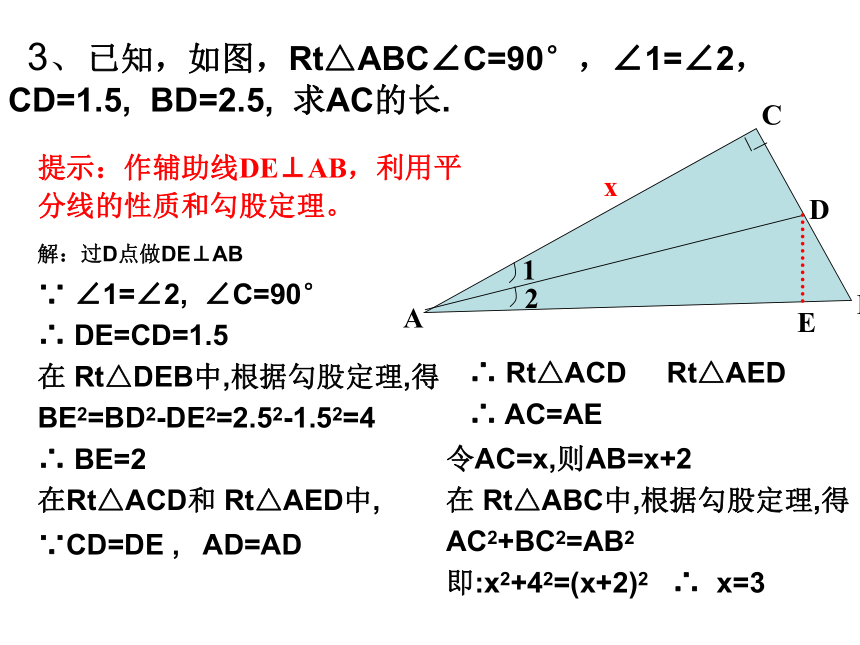
提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。
解:过D点做DE⊥AB
∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4
∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD
∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得
AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3
x
3、已知,如图,Rt△ABC∠C=90°,∠1=∠2,CD=1.5, BD=2.5, 求AC的长.
E
A
A’
B
B’
C
D
D’
C’
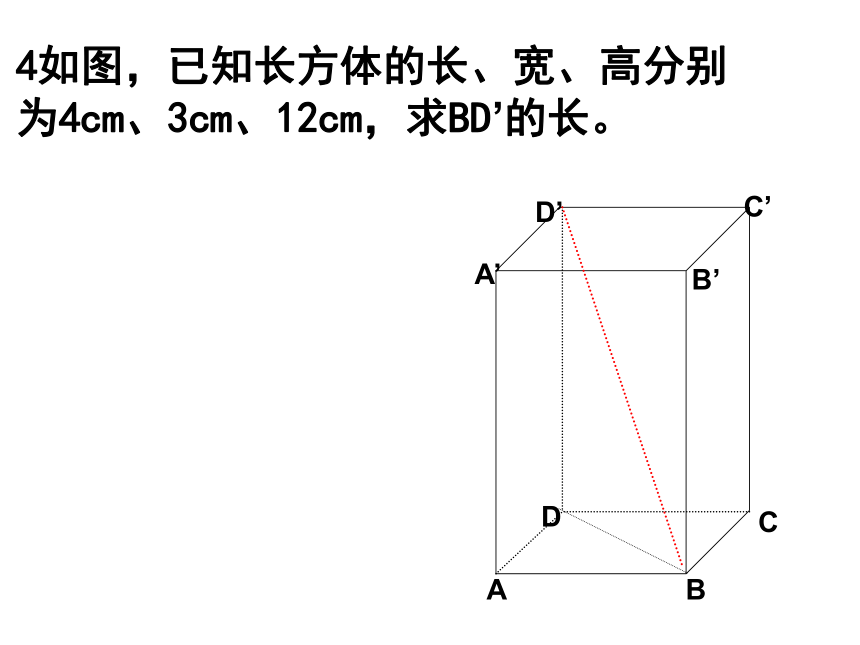
4如图,已知长方体的长、宽、高分别为4cm、3cm、12cm,求BD’的长。
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
6.小明学了利用勾股定理在数轴上作一个无理数后,在数轴上的2个单位长度的位置找一个点D,然后过点D作一条垂直于数轴的线段CD,CD为3个单位长度,以原点为圆心,原点到点C的距离为半径作弧,交数轴于一点(如图),则该点位置大致在数轴上
( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
B
D
7.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,则AB边上的高为_______.
解:∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,
∴∠CDB=150°-60°=90°,
∴△BCD是直角三角形.
又∵四边形的周长为32cm,
∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=xcm,则BC=(16-x)cm,
由勾股定理得82+x2=(16-x)2,
解得x=6.∴S△BCD= ×6×8=24(cm2).
4.如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
8.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿 AC折叠,点D落在点D′处,求重叠部分△AFC的
面积.
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,
解得x=3.
∴AF=AB-FB=8-3=5,
∴S△AFC= AF?BC=10.
图?
能力提升:
9.问题背景:
在△ABC中,AB、BC、AC三边的长分别为 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)求△ABC的面积;
(2)若△ABC三边的长分别为 (a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
解:如图,
思维拓展:
∴△ABC即为所求,
图②
A
B
C
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
互逆定理
本章知识框图:
勾股定理
勾股定理的逆定理
直角三角形的判定
直角三角形边长的数量关系
1.勾股定理
直角三角形两直角边a、 b的平方和,等于斜边c的平方。
2.勾股定理的逆定理
如果三角形三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股数.
熟记常见的勾股数(如3、4、5)
3.勾股数
4.互逆命题与互逆定理的概念
勾股定理
勾股定理的逆定理
题设
在Rt△ABC 中,∠C=900
在△ABC 中, 三边a,b,c满足a2+b2=c2
结论
a2+b2=c2
∠C=900
作用
1.用勾股定理进行计算
2.证明与平方有关的问题3.解决实际问题
1.判断某三角形是否为直角三角形(3种)
2.解决实际问题
联系
1.两个定理都与“三角形的三边关系a2+b2=c2”有关;
2.都与直角三角形有关;
3.都是数形结合思想的体现。
1、如图所示,图中所有三角形是直角三角形,所有四边形是正方形,s1=9,s3=144,s4=169 ,则s2= .
16
2、如图,直线上有三个正方形,若的面积分别为5和11,则的面积为( )
6
D
A
C
B
1
2
提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。
解:过D点做DE⊥AB
∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4
∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD
∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得
AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3
x
3、已知,如图,Rt△ABC∠C=90°,∠1=∠2,CD=1.5, BD=2.5, 求AC的长.
E
A
A’
B
B’
C
D
D’
C’
4如图,已知长方体的长、宽、高分别为4cm、3cm、12cm,求BD’的长。
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
6.小明学了利用勾股定理在数轴上作一个无理数后,在数轴上的2个单位长度的位置找一个点D,然后过点D作一条垂直于数轴的线段CD,CD为3个单位长度,以原点为圆心,原点到点C的距离为半径作弧,交数轴于一点(如图),则该点位置大致在数轴上
( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
B
D
7.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,则AB边上的高为_______.
解:∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,
∴∠CDB=150°-60°=90°,
∴△BCD是直角三角形.
又∵四边形的周长为32cm,
∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=xcm,则BC=(16-x)cm,
由勾股定理得82+x2=(16-x)2,
解得x=6.∴S△BCD= ×6×8=24(cm2).
4.如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
8.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿 AC折叠,点D落在点D′处,求重叠部分△AFC的
面积.
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,
解得x=3.
∴AF=AB-FB=8-3=5,
∴S△AFC= AF?BC=10.
图?
能力提升:
9.问题背景:
在△ABC中,AB、BC、AC三边的长分别为 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)求△ABC的面积;
(2)若△ABC三边的长分别为 (a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
解:如图,
思维拓展:
∴△ABC即为所求,
图②
A
B
C
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
