2020-2021学年人教版七年级数学下册5.3.1平行线的性质课件(19张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册5.3.1平行线的性质课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 961.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-10 00:49:04 | ||
图片预览



文档简介
2.与角有关的三个判定方法,它
们是先知道什么? 后得到什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
1.平行线的判定方法有哪些?
温故知新
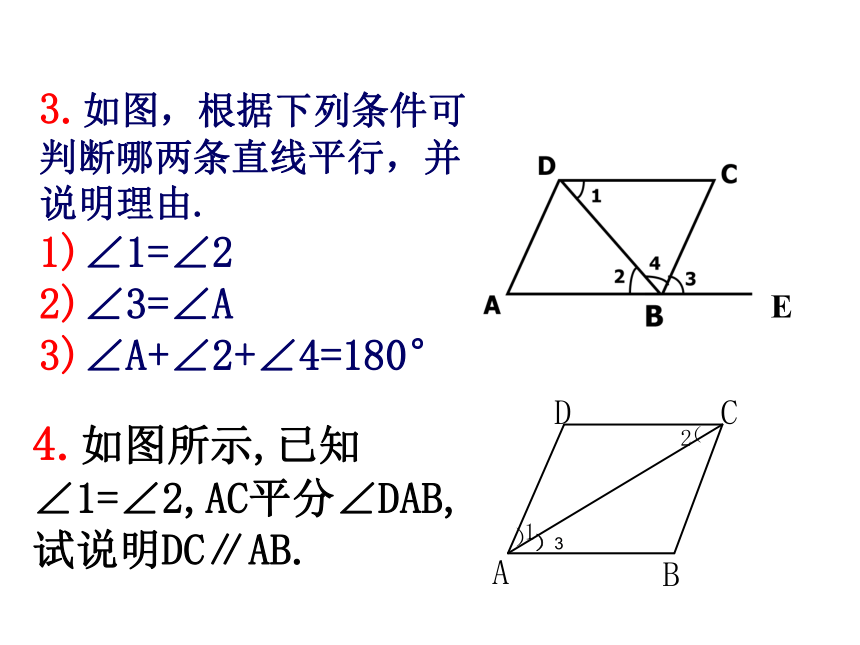
3.如图,根据下列条件可判断哪两条直线平行,并说明理由. 1)∠1=∠2 2)∠3=∠A 3)∠A+∠2+∠4=180°
4.如图所示,已知∠1=∠2,AC平分∠DAB, 试说明DC∥AB.
3
)
)
(
E
2.测量这8个角的大小,记录下来.
1.先画出两条平行线,再画一条直线与它们相交,并标出所形成的8个角.
3.你发现图中的同位角,内错角,同旁内角具有怎样的数量关系?小组交流一下.
b
1
2
4
3
5
6
8
7
a
c
探究 交流 归纳
模仿平行线的判定,你能归纳一下你的发现吗?
平行线的性质1
符号语言:
∵ AB∥CD(已知)
两条平行线被第三条直线所截,同位角相等.
简单说:两直线平行,同位角相等.
∴ ∠1=∠2
(两直线平行,同位角相等)
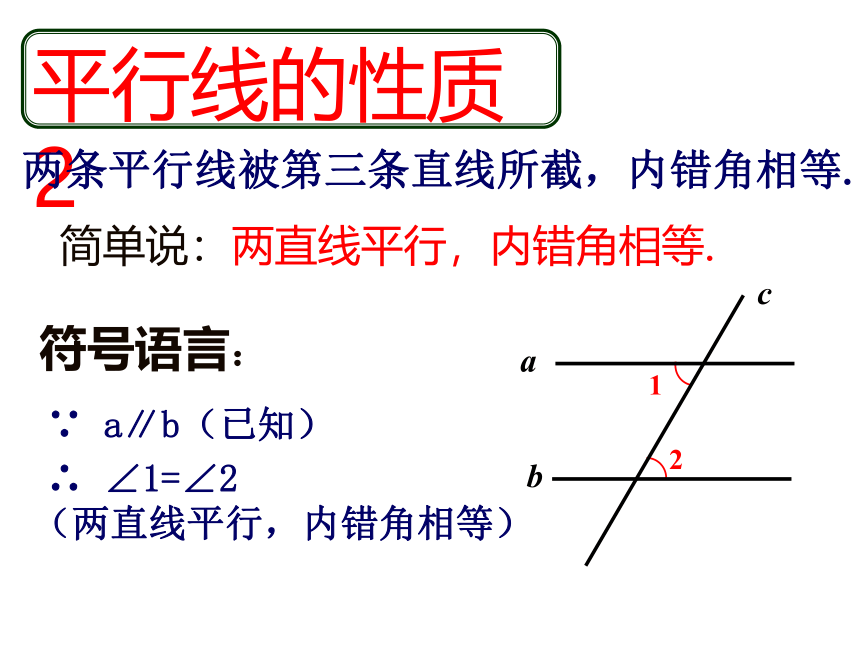
平行线的性质2
符号语言:
∵ a∥b(已知)
两条平行线被第三条直线所截,内错角相等.
简单说:两直线平行,内错角相等.
a
b
c
2
1
∴ ∠1=∠2
(两直线平行,内错角相等)
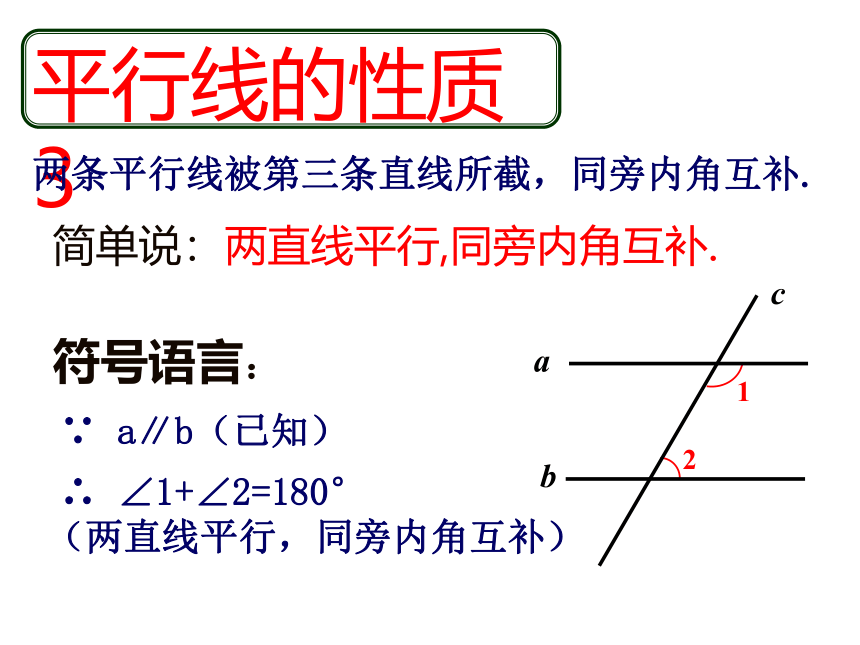
平行线的性质3
符号语言:
∵ a∥b(已知)
两条平行线被第三条直线所截,同旁内角互补.
简单说:两直线平行,同旁内角互补.
a
b
c
2
1
∴ ∠1+∠2=180°
(两直线平行,同旁内角互补)
平行线的“判定”与“性质”有什么不同?
已知角之间的关系(相等或互补), 得到两直线平行是平行线的判定.
已知两直线平行, 得到角之间的关系(相等或互补)
是平行线的性质.
1.已知直线a∥b,∠1=130°,求∠7的度数.
两条平行线被第三条直线所截得的8个角,
已知1个角的度数,可以求出其余7个角的度数.
b
4
3
1
2
8
7
5
6
a
c
小试牛刀
你能求出剩下的6个角的度数吗?
2.如图,在四边形ABCD中,已知AB//CD,∠B=60?,求∠C 的度数. 能否求得∠A的度数?
A
B
C
D
A
B
C
D
E
3.已知∠C=∠1,BE平分∠ABC,
试说明∠2=∠4.
1
2
3
4
C
B
A
D
4.如图是梯形有上底的一部分.已经量得 ?A=115°,?D=100°,梯形另外两个角 各是多少度?
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
(等量代换)
1.已知∠ADE=60°,∠B=60°,∠AED=50°.
求∠C的度数.
再接再厉
2.如图,AB∥CD,AD∥BC,分别找出图中相等或互补的角.
C
A
B
D
3.如图,工人在修一条高速公路时前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向?
4.已知:如图,∠1=∠2,∠C=∠D, 求证:∠A=∠F
证明:∵∠1=∠2( )
∠2=∠3( )
∴∠1=∠__( )
∴BD∥CE( )
∴∠C=∠4( )
∵∠C=∠D( )
∴∠D=∠4( )
∴DF∥AC( )
∴∠A=∠F( )
3
2
B
A
C
D
E
F
1
4
(
︺
︺
︹
如图,若AB//CD,你能确定∠B、∠D与∠BED的大小关系吗?交流你的看法.
B
C
E
A
拓展提高
D
F
……
课后练习
P20 练习 T1.
们是先知道什么? 后得到什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
1.平行线的判定方法有哪些?
温故知新
3.如图,根据下列条件可判断哪两条直线平行,并说明理由. 1)∠1=∠2 2)∠3=∠A 3)∠A+∠2+∠4=180°
4.如图所示,已知∠1=∠2,AC平分∠DAB, 试说明DC∥AB.
3
)
)
(
E
2.测量这8个角的大小,记录下来.
1.先画出两条平行线,再画一条直线与它们相交,并标出所形成的8个角.
3.你发现图中的同位角,内错角,同旁内角具有怎样的数量关系?小组交流一下.
b
1
2
4
3
5
6
8
7
a
c
探究 交流 归纳
模仿平行线的判定,你能归纳一下你的发现吗?
平行线的性质1
符号语言:
∵ AB∥CD(已知)
两条平行线被第三条直线所截,同位角相等.
简单说:两直线平行,同位角相等.
∴ ∠1=∠2
(两直线平行,同位角相等)
平行线的性质2
符号语言:
∵ a∥b(已知)
两条平行线被第三条直线所截,内错角相等.
简单说:两直线平行,内错角相等.
a
b
c
2
1
∴ ∠1=∠2
(两直线平行,内错角相等)
平行线的性质3
符号语言:
∵ a∥b(已知)
两条平行线被第三条直线所截,同旁内角互补.
简单说:两直线平行,同旁内角互补.
a
b
c
2
1
∴ ∠1+∠2=180°
(两直线平行,同旁内角互补)
平行线的“判定”与“性质”有什么不同?
已知角之间的关系(相等或互补), 得到两直线平行是平行线的判定.
已知两直线平行, 得到角之间的关系(相等或互补)
是平行线的性质.
1.已知直线a∥b,∠1=130°,求∠7的度数.
两条平行线被第三条直线所截得的8个角,
已知1个角的度数,可以求出其余7个角的度数.
b
4
3
1
2
8
7
5
6
a
c
小试牛刀
你能求出剩下的6个角的度数吗?
2.如图,在四边形ABCD中,已知AB//CD,∠B=60?,求∠C 的度数. 能否求得∠A的度数?
A
B
C
D
A
B
C
D
E
3.已知∠C=∠1,BE平分∠ABC,
试说明∠2=∠4.
1
2
3
4
C
B
A
D
4.如图是梯形有上底的一部分.已经量得 ?A=115°,?D=100°,梯形另外两个角 各是多少度?
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
(等量代换)
1.已知∠ADE=60°,∠B=60°,∠AED=50°.
求∠C的度数.
再接再厉
2.如图,AB∥CD,AD∥BC,分别找出图中相等或互补的角.
C
A
B
D
3.如图,工人在修一条高速公路时前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向?
4.已知:如图,∠1=∠2,∠C=∠D, 求证:∠A=∠F
证明:∵∠1=∠2( )
∠2=∠3( )
∴∠1=∠__( )
∴BD∥CE( )
∴∠C=∠4( )
∵∠C=∠D( )
∴∠D=∠4( )
∴DF∥AC( )
∴∠A=∠F( )
3
2
B
A
C
D
E
F
1
4
(
︺
︺
︹
如图,若AB//CD,你能确定∠B、∠D与∠BED的大小关系吗?交流你的看法.
B
C
E
A
拓展提高
D
F
……
课后练习
P20 练习 T1.
