2020-2021学年教科版高一物理必修2第二章第2节匀速圆周运动的向心力和向心加速度课件18张PPT
文档属性
| 名称 | 2020-2021学年教科版高一物理必修2第二章第2节匀速圆周运动的向心力和向心加速度课件18张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-10 00:00:00 | ||
图片预览




文档简介
复习提问
上节学习了匀速圆周运动以及描述其快慢的有关物理量,回忆:匀速圆周运动是匀速运动吗?其中的匀速是何意思?
匀速圆周运动是一变速运动,故匀速圆周运动所受的合力一定不为零,一定具有加速度。
本节课学习匀速圆周运动的受力及加速度的特点。
第二章 匀速圆周运动
第二节 匀速圆周运动的向心力
和向心加速度
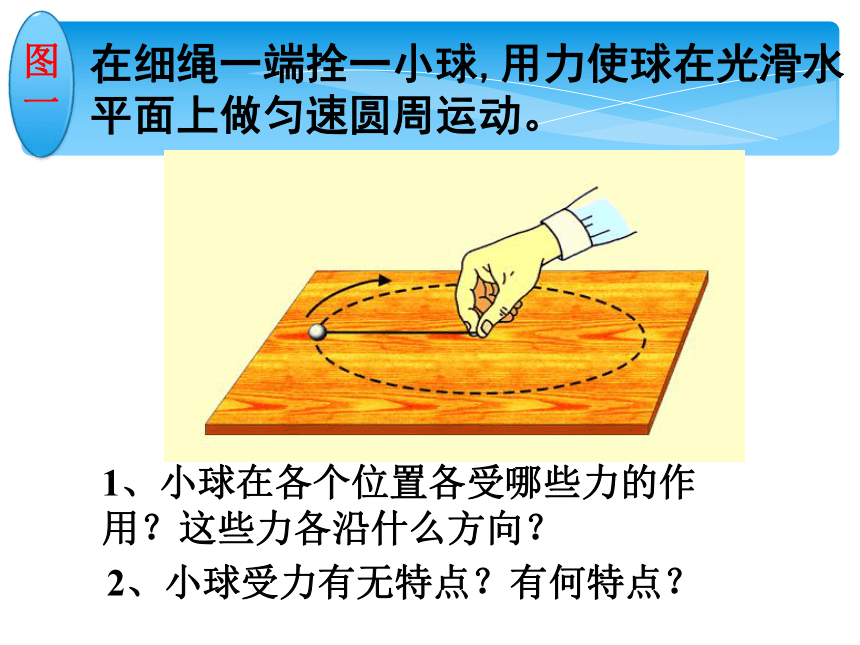
2、小球受力有无特点?有何特点?
1、小球在各个位置各受哪些力的作
用?这些力各沿什么方向?
在细绳一端拴一小球,用力使球在光滑水平面上做匀速圆周运动。
图一
O
F
F
F
V
V
V
O
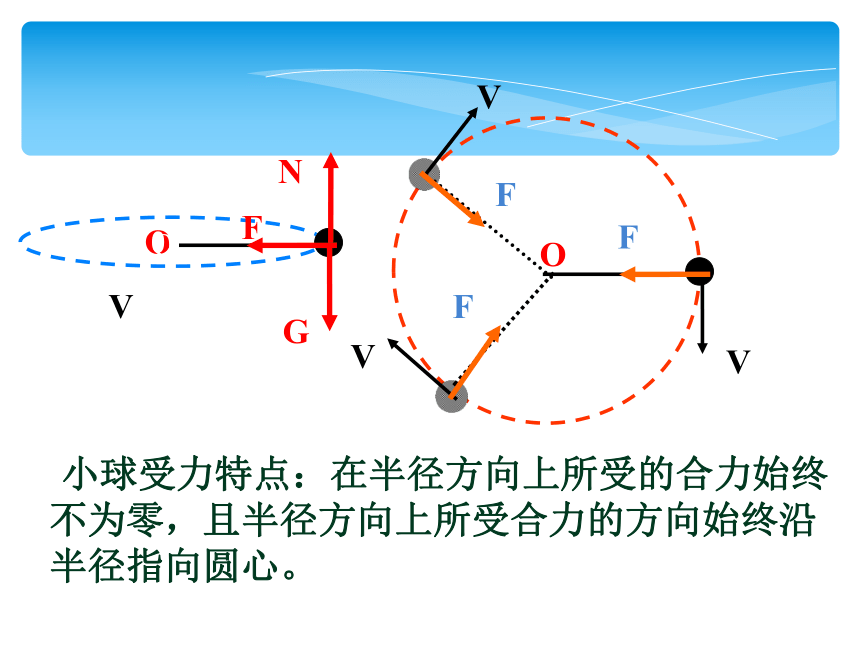
小球受力特点:在半径方向上所受的合力始终不为零,且半径方向上所受合力的方向始终沿半径指向圆心。
O
O
F
V
G
N
旋转秋千
G
F
F1
F2
图二
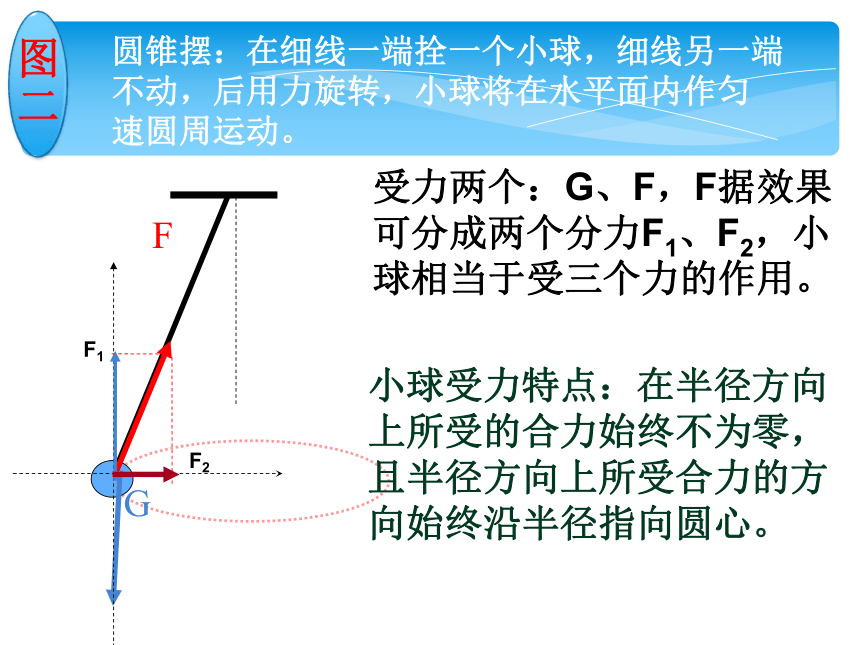
圆锥摆:在细线一端拴一个小球,细线另一端
不动,后用力旋转,小球将在水平面内作匀
速圆周运动。
受力两个:G、F,F据效果可分成两个分力F1、F2,小球相当于受三个力的作用。
小球受力特点:在半径方向上所受的合力始终不为零,且半径方向上所受合力的方向始终沿半径指向圆心。
人造卫 星 绕 地 球 运 行
F
F
F
匀速圆周运动的受力特点:
在半径方向上所受的合力始终不为零,且半径方向上所受合力的方向始终沿半径指向圆心。
向心力:作匀速圆周运动的物体在半径方向上所受的合力,叫做向心力。
一、向心力
向心力不是不同于重力、弹力、摩擦力等力的一种新的力,实质上只是物体所受的重力、弹力、摩擦力等力中在半径方向上的某一个力,或者某个力的分力,或某几个分力的的合力,只是由于它们的方向始终沿半
注意:
1、向心力的实质:
径指向圆心,故才形象的另外给它取了个名字:向心力。无论是什么样的力,只要它的方向是沿半径指向圆心,都可称之为向心力。向心力是根据力的作用效果来命名的一种效果力。以后对圆周运动进行受力分析时,分析了重力、弹力、摩擦力、已知外力等力后,不能再分析一个向心力。
2、匀速圆周运动的合力等于向心力。
转动手柄
变速轮塔
变速轮塔
长槽
短槽
横臂挡板
弹簧测力套筒
标尺
向心力演示器
传动皮带
二、向心力的大小
G
FN
F?
F
装置用途:装置中有两个变速塔轮,它们都带有几个半径不同的圆盘,这些圆盘可通过皮带连接,转动手柄将同时转动。一个塔轮上带了一个水平长槽,另一个带了一个水平短槽,槽上都带了个挡板和横臂,横臂都与各自的弹簧测力筒的外筒相连。若在挡板处放一个小球,槽转动起来后,小球将作圆周运动,向心力将由挡板对小球向内的压力充当。同时小球对挡板有一向外的压力,在这个压力作用下,横臂向下转动,带动外筒向下运动,内筒露出的格数,反映小球和挡板间的压力(即小球的向心力)的大小。
(1)实验探究
?把两个变速塔轮的两个相同圆盘用皮带连起来,把两个相同的钢球分别放在长短槽上离盘心距离不等的两档板处。两小球质量相同,作匀速圆周运动的角速度相同,但半径不同,半径之比为2:1。
?把两个变速塔轮的两个相同圆盘用皮带连起来,把一个胶球和一个钢球分别放在长短槽上离各自盘心等距离的两档板处。两小球质量不同,作匀速圆周运动的角速度和半径相同。
结论:
结论:
?把两个变速塔轮的两个不同圆盘用皮带连起来,把两个相同的钢球分别放在长短槽上离盘心等距离的两档板处。两小球质量相同,作匀速圆周运动半径相同,但角速度不同。
F ∝m
F ∝ω2
F ∝r
结论:
(2)总结:匀速圆周运动的向心力的大小F与质量m、角速度ω和半径r之间存在怎样的关系?用数学公式可以怎么表示呢?
各量均采用国际单位制表示,则k=1.
由
得:
匀速圆周运动向心力大小的周期、频率表达式:
=mωv
(向心力的角速度表达式)
讨论与交流P27:
向心力的大小: F = mω2r
F = mv2/r
向心力大小的上述两个表达式中,一个式子中向心力的大小与半径成正比,而另一个式子中向心力的大小与半径成反比,它们相互矛盾吗?
向心力与r成正比的条件:ω相同。若ω不同,向心力与半径无正比关系;向心力与r成反比的条件;v相同。若v不同,向心力与半径无反比关系。
例、线的一端系一个重物,手执线的另一端,使重物在光滑水平桌面上做匀速圆周运动。当转速(角速度)相同时,线长易断,还是线短易断?为什么?如果重物运动时系线被桌上的一个钉子挡住,随后重物以不变的速率在系线的牵引下绕钉子做圆周运动。系线碰钉子后,是钉子离重物越远线易断,还是离重物越近线易断?为什么?
二、向心加速度
3、大小:
根据牛顿第二定律
1、向心加速度:做匀速圆周运动的物体,在半径方向上的加速度。(或:向心力产生的加速度)
匀速圆周运动的加速度等于向心加速度
由向心力公式
匀速圆周运动在半径方向上所受的合力始终不为零,且合力的方向始终沿半径指向圆心,故据牛顿第二定律知:匀速圆周运动在半径方向上必有加速度,且加速度的方向也始终沿半径指向圆心,也形象地称之为向心加速度。
=mωv
2、方向:始终沿半径指向圆心。
得:
或a=ωv
匀速圆周运动的加速度大小虽不变,但方向不断改变,故加速度不断改变,故匀速圆周运动是一种匀速率、变加速曲线运动。
说明:
上述三式对变速圆周运动也适用,但对变
速圆周运动的某个位置使用上述三式时,v、
只能使用这个位置的瞬时值。
ω
只对匀速圆周运动适用,对变速圆周运动不适用
或a=ωv
小结:
一、向心力
1、定义:做匀速圆周运动的物体在半径方向上所受的始终沿半径指向圆心方向的合力,叫做向心力。
2、方向:与速度垂直,始终指向圆心。
3、大小:
或
二、向心加速度
1、定义:
3、大小:
做匀速圆周运动的物体,在半径方向上的加速度。
2、方向:
始终沿半径指向圆心
4、物理意义:
描述做圆周运动的物体线速度方向改变的快慢。
上节学习了匀速圆周运动以及描述其快慢的有关物理量,回忆:匀速圆周运动是匀速运动吗?其中的匀速是何意思?
匀速圆周运动是一变速运动,故匀速圆周运动所受的合力一定不为零,一定具有加速度。
本节课学习匀速圆周运动的受力及加速度的特点。
第二章 匀速圆周运动
第二节 匀速圆周运动的向心力
和向心加速度
2、小球受力有无特点?有何特点?
1、小球在各个位置各受哪些力的作
用?这些力各沿什么方向?
在细绳一端拴一小球,用力使球在光滑水平面上做匀速圆周运动。
图一
O
F
F
F
V
V
V
O
小球受力特点:在半径方向上所受的合力始终不为零,且半径方向上所受合力的方向始终沿半径指向圆心。
O
O
F
V
G
N
旋转秋千
G
F
F1
F2
图二
圆锥摆:在细线一端拴一个小球,细线另一端
不动,后用力旋转,小球将在水平面内作匀
速圆周运动。
受力两个:G、F,F据效果可分成两个分力F1、F2,小球相当于受三个力的作用。
小球受力特点:在半径方向上所受的合力始终不为零,且半径方向上所受合力的方向始终沿半径指向圆心。
人造卫 星 绕 地 球 运 行
F
F
F
匀速圆周运动的受力特点:
在半径方向上所受的合力始终不为零,且半径方向上所受合力的方向始终沿半径指向圆心。
向心力:作匀速圆周运动的物体在半径方向上所受的合力,叫做向心力。
一、向心力
向心力不是不同于重力、弹力、摩擦力等力的一种新的力,实质上只是物体所受的重力、弹力、摩擦力等力中在半径方向上的某一个力,或者某个力的分力,或某几个分力的的合力,只是由于它们的方向始终沿半
注意:
1、向心力的实质:
径指向圆心,故才形象的另外给它取了个名字:向心力。无论是什么样的力,只要它的方向是沿半径指向圆心,都可称之为向心力。向心力是根据力的作用效果来命名的一种效果力。以后对圆周运动进行受力分析时,分析了重力、弹力、摩擦力、已知外力等力后,不能再分析一个向心力。
2、匀速圆周运动的合力等于向心力。
转动手柄
变速轮塔
变速轮塔
长槽
短槽
横臂挡板
弹簧测力套筒
标尺
向心力演示器
传动皮带
二、向心力的大小
G
FN
F?
F
装置用途:装置中有两个变速塔轮,它们都带有几个半径不同的圆盘,这些圆盘可通过皮带连接,转动手柄将同时转动。一个塔轮上带了一个水平长槽,另一个带了一个水平短槽,槽上都带了个挡板和横臂,横臂都与各自的弹簧测力筒的外筒相连。若在挡板处放一个小球,槽转动起来后,小球将作圆周运动,向心力将由挡板对小球向内的压力充当。同时小球对挡板有一向外的压力,在这个压力作用下,横臂向下转动,带动外筒向下运动,内筒露出的格数,反映小球和挡板间的压力(即小球的向心力)的大小。
(1)实验探究
?把两个变速塔轮的两个相同圆盘用皮带连起来,把两个相同的钢球分别放在长短槽上离盘心距离不等的两档板处。两小球质量相同,作匀速圆周运动的角速度相同,但半径不同,半径之比为2:1。
?把两个变速塔轮的两个相同圆盘用皮带连起来,把一个胶球和一个钢球分别放在长短槽上离各自盘心等距离的两档板处。两小球质量不同,作匀速圆周运动的角速度和半径相同。
结论:
结论:
?把两个变速塔轮的两个不同圆盘用皮带连起来,把两个相同的钢球分别放在长短槽上离盘心等距离的两档板处。两小球质量相同,作匀速圆周运动半径相同,但角速度不同。
F ∝m
F ∝ω2
F ∝r
结论:
(2)总结:匀速圆周运动的向心力的大小F与质量m、角速度ω和半径r之间存在怎样的关系?用数学公式可以怎么表示呢?
各量均采用国际单位制表示,则k=1.
由
得:
匀速圆周运动向心力大小的周期、频率表达式:
=mωv
(向心力的角速度表达式)
讨论与交流P27:
向心力的大小: F = mω2r
F = mv2/r
向心力大小的上述两个表达式中,一个式子中向心力的大小与半径成正比,而另一个式子中向心力的大小与半径成反比,它们相互矛盾吗?
向心力与r成正比的条件:ω相同。若ω不同,向心力与半径无正比关系;向心力与r成反比的条件;v相同。若v不同,向心力与半径无反比关系。
例、线的一端系一个重物,手执线的另一端,使重物在光滑水平桌面上做匀速圆周运动。当转速(角速度)相同时,线长易断,还是线短易断?为什么?如果重物运动时系线被桌上的一个钉子挡住,随后重物以不变的速率在系线的牵引下绕钉子做圆周运动。系线碰钉子后,是钉子离重物越远线易断,还是离重物越近线易断?为什么?
二、向心加速度
3、大小:
根据牛顿第二定律
1、向心加速度:做匀速圆周运动的物体,在半径方向上的加速度。(或:向心力产生的加速度)
匀速圆周运动的加速度等于向心加速度
由向心力公式
匀速圆周运动在半径方向上所受的合力始终不为零,且合力的方向始终沿半径指向圆心,故据牛顿第二定律知:匀速圆周运动在半径方向上必有加速度,且加速度的方向也始终沿半径指向圆心,也形象地称之为向心加速度。
=mωv
2、方向:始终沿半径指向圆心。
得:
或a=ωv
匀速圆周运动的加速度大小虽不变,但方向不断改变,故加速度不断改变,故匀速圆周运动是一种匀速率、变加速曲线运动。
说明:
上述三式对变速圆周运动也适用,但对变
速圆周运动的某个位置使用上述三式时,v、
只能使用这个位置的瞬时值。
ω
只对匀速圆周运动适用,对变速圆周运动不适用
或a=ωv
小结:
一、向心力
1、定义:做匀速圆周运动的物体在半径方向上所受的始终沿半径指向圆心方向的合力,叫做向心力。
2、方向:与速度垂直,始终指向圆心。
3、大小:
或
二、向心加速度
1、定义:
3、大小:
做匀速圆周运动的物体,在半径方向上的加速度。
2、方向:
始终沿半径指向圆心
4、物理意义:
描述做圆周运动的物体线速度方向改变的快慢。
