人教七上数学1.5.1-有理数的乘方课件(共36张ppt)
文档属性
| 名称 | 人教七上数学1.5.1-有理数的乘方课件(共36张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 21:25:05 | ||
图片预览











文档简介
(共36张PPT)
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致我亲爱的同学们
有理数的乘方(1)
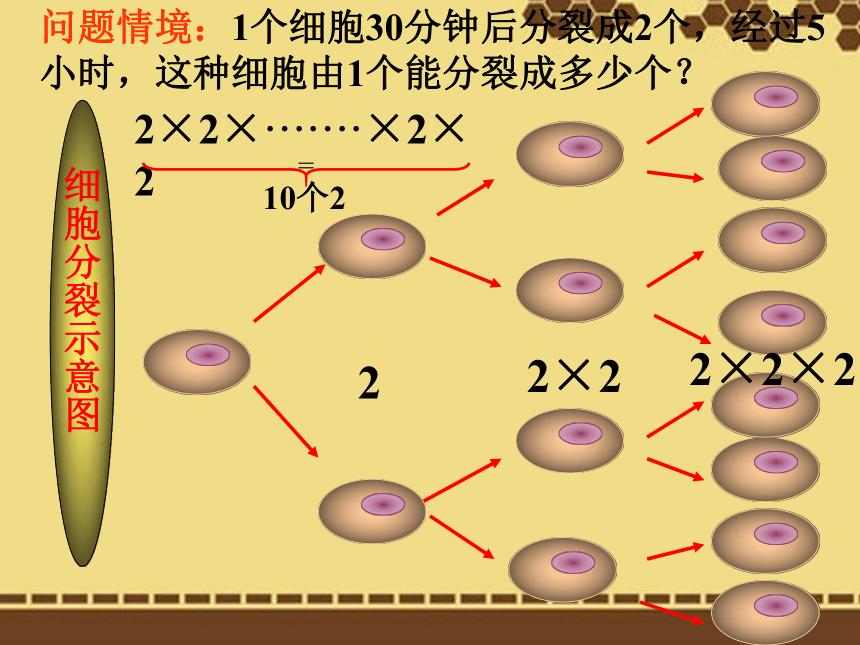
细胞分裂示意图
问题情境:1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
问题一:2
×
2×
2×
2
×
2
简记为
动动脑
25
问题二:a×
a×
a
×
a
×
a
×
a
×
a简记为
问题三:
a×a×a×……×a
简记为
n个a
a7
an
2
×2
×…
×2
×2
10个2
记作210
a×a
×…
×a
×a
n个a
乘方:求几个相同因数的积的运算,叫做乘方
10
有理数的乘方
记作
an
a
n
底数
幂
指数
a
n
读作a的n次方
看作是a的n次方的结果时,也可读作a的n次幂
(乘方的结果叫做幂)
其中a代表相乘的因数,n代表
相乘因数的个数即:
a×a×a···×a
n个a
an
=
乘方的意义
也就是a的n次方等于n个a相乘
运算
加法
减法
乘法
除法
乘方
结果
和
差
积
商
幂
(1)在64中,底数是___,指数是____;
(3)在(-6)4中,底数是
___,
指数是___;
写出下列各幂的底数与指数:
-6
4
a
4
6
4
(2)在a4中,底数是___,指数是____;
5
(4)在
中,底数是____,指数是____;
返回
下一张
上一张
退出
一个数可以看作这个数本身的一次方,
例如:5就是51,指数是1通常省略不写
2次方又叫平方,3次方又叫立方。
1、把下列相同的因数写成幂的形式,并说明底数和指数
2、
写成几个相同因数相乘的形式
注意:(1)负数的乘方,在书写时一
定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法。
(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来。
1
2
(
)
3
如:
、(-3)2
3
2
(-3)
2
与
结果相等吗?
-3
2
=-9
=9
(-3)
2
3
2
读作 的相反数,而
读作-3的
平方
(-3)
2
所以
-3
2
思考:说说下列各数的意义,它们一样吗?
思考:说说下列各数的意义,它们一样吗?
例1
计算:
(1)
(2)
(3)
(1)
(2)
(3)
解:
计算下列各题:
(1)
53
(2)
4
2
(3)
(-3)4
(4)
(
5
)
)
(
2
(-
)
3
=
=-
=125
=16
=81
观察例1和左边各式的计算结果,你能发现乘方运算的符号有什么规律?
想一想:
乘方运算的符号规律
正数的任何次幂都是正数
负数的偶次幂是正数,奇次幂是负数
确定下列幂的正负
+
-
+
+
-
试一试
(1)
(2)
(3)
(4)
(5)
(6)
=1
=1
=-1
=1
=1
=-1
试一试
口答
(2)
-1的幂很有规律:
-1的奇次幂是-1
,
-1的偶次幂是1。
(1)
1的任何次幂都为
1。
100
1000;
100
-1000
10000
返回
下一张
上一张
退出
抢答练习:
计算
10000
你能发现什么规律吗?
(1)正数的任次幂为正;负数的偶次
幂为正
奇次幂为负
0.01;
-0.001
返回
下一张
上一张
退出
抢答练习:
计算
0.0001
0.01;
0.001;
0.0001
你能发现什么规律吗?
练习:用〉
、〈
或=号填空
0
0
0
0
>
>
<
=
0的任何正整数次幂都是0
小结:
你能告诉我这节课的收获吗?
乘方运算的法则:
正数的任何次幂都是正数;
0的任何正整数次幂都是0;负数的奇次幂是负数,负数的偶次幂是正数
乘方:求几个相同因数的积的运算,叫做乘方
返回
下一张
上一张
退出
珠穆朗玛峰是世界的最高峰,
它的海拔高度是8844米。把一张
足够大的厚度为0.1毫米的纸,
连续对折30次的厚度能超过珠穆
朗玛峰。这是真的吗?
这张纸对折30次后能超过珠穆朗玛峰吗?
如果把足够长的厚0.1毫米的纸折叠30次后有10万多米高,有12个珠穆朗玛峰高。
分析:
0.1毫米×230=0.1毫米×1073741824
=107374.1824米
8844.43
×12=106133.16
这下你该
相信了吧!
这节课你学会了一种什么运算?你有何体会?
反思
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
填表:
底数
-1
2
10
指数
3
5
4
幂
(-4)3
0.34
(-1)3
25
-4
3
4
0.3
104
判断:(对的画“√”,错的画“×”.)
(1)
32
=
3×2
=
6;
(
)
(2)
(-2)3
=
(-3)2;
(
)
(3)
-32
=
(-3)2;
(
)
(4)
;
(
)
(5)
.
(
)
X
X
X
X
X
32
=
3×3=9
(-2)3
=-8;
(-3)2=9
-32
=-9;
(-3)2=9
-24=-2×2×2×2=-16
(-4)2底数是______指数是______(-4)2=_______
-4
2
16
34表示___个___
相乘
4
3
(-2)3=______
-8
(+1)2003
-(-
1)2002=___
0
-
14+1=______
0
3或-3
______的平方等于9
不计算下列各式的值,你能确定其符号吗?
你能得到什么规律吗?说出你的根据.
(1)(-2)51
;(2)(-2)50
;
(3)250
;
(4)251;
(5)02
020
;(6)12
021.
你能迅速判断下列各幂的正负吗?
手工拉面是我国的传统面食.制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣,如此反复操作,连续扣六七次后便成了许多细细的面条.假如拉扣了6次,你能算出共有多少根面条吗?
第一次
拉扣后
第二次
拉扣后
第三次
拉扣后
…
你认为国王的国库里有这么多米吗?
猜猜看
…
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致我亲爱的同学们
有理数的乘方(1)
细胞分裂示意图
问题情境:1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
问题一:2
×
2×
2×
2
×
2
简记为
动动脑
25
问题二:a×
a×
a
×
a
×
a
×
a
×
a简记为
问题三:
a×a×a×……×a
简记为
n个a
a7
an
2
×2
×…
×2
×2
10个2
记作210
a×a
×…
×a
×a
n个a
乘方:求几个相同因数的积的运算,叫做乘方
10
有理数的乘方
记作
an
a
n
底数
幂
指数
a
n
读作a的n次方
看作是a的n次方的结果时,也可读作a的n次幂
(乘方的结果叫做幂)
其中a代表相乘的因数,n代表
相乘因数的个数即:
a×a×a···×a
n个a
an
=
乘方的意义
也就是a的n次方等于n个a相乘
运算
加法
减法
乘法
除法
乘方
结果
和
差
积
商
幂
(1)在64中,底数是___,指数是____;
(3)在(-6)4中,底数是
___,
指数是___;
写出下列各幂的底数与指数:
-6
4
a
4
6
4
(2)在a4中,底数是___,指数是____;
5
(4)在
中,底数是____,指数是____;
返回
下一张
上一张
退出
一个数可以看作这个数本身的一次方,
例如:5就是51,指数是1通常省略不写
2次方又叫平方,3次方又叫立方。
1、把下列相同的因数写成幂的形式,并说明底数和指数
2、
写成几个相同因数相乘的形式
注意:(1)负数的乘方,在书写时一
定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法。
(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来。
1
2
(
)
3
如:
、(-3)2
3
2
(-3)
2
与
结果相等吗?
-3
2
=-9
=9
(-3)
2
3
2
读作 的相反数,而
读作-3的
平方
(-3)
2
所以
-3
2
思考:说说下列各数的意义,它们一样吗?
思考:说说下列各数的意义,它们一样吗?
例1
计算:
(1)
(2)
(3)
(1)
(2)
(3)
解:
计算下列各题:
(1)
53
(2)
4
2
(3)
(-3)4
(4)
(
5
)
)
(
2
(-
)
3
=
=-
=125
=16
=81
观察例1和左边各式的计算结果,你能发现乘方运算的符号有什么规律?
想一想:
乘方运算的符号规律
正数的任何次幂都是正数
负数的偶次幂是正数,奇次幂是负数
确定下列幂的正负
+
-
+
+
-
试一试
(1)
(2)
(3)
(4)
(5)
(6)
=1
=1
=-1
=1
=1
=-1
试一试
口答
(2)
-1的幂很有规律:
-1的奇次幂是-1
,
-1的偶次幂是1。
(1)
1的任何次幂都为
1。
100
1000;
100
-1000
10000
返回
下一张
上一张
退出
抢答练习:
计算
10000
你能发现什么规律吗?
(1)正数的任次幂为正;负数的偶次
幂为正
奇次幂为负
0.01;
-0.001
返回
下一张
上一张
退出
抢答练习:
计算
0.0001
0.01;
0.001;
0.0001
你能发现什么规律吗?
练习:用〉
、〈
或=号填空
0
0
0
0
>
>
<
=
0的任何正整数次幂都是0
小结:
你能告诉我这节课的收获吗?
乘方运算的法则:
正数的任何次幂都是正数;
0的任何正整数次幂都是0;负数的奇次幂是负数,负数的偶次幂是正数
乘方:求几个相同因数的积的运算,叫做乘方
返回
下一张
上一张
退出
珠穆朗玛峰是世界的最高峰,
它的海拔高度是8844米。把一张
足够大的厚度为0.1毫米的纸,
连续对折30次的厚度能超过珠穆
朗玛峰。这是真的吗?
这张纸对折30次后能超过珠穆朗玛峰吗?
如果把足够长的厚0.1毫米的纸折叠30次后有10万多米高,有12个珠穆朗玛峰高。
分析:
0.1毫米×230=0.1毫米×1073741824
=107374.1824米
8844.43
×12=106133.16
这下你该
相信了吧!
这节课你学会了一种什么运算?你有何体会?
反思
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
填表:
底数
-1
2
10
指数
3
5
4
幂
(-4)3
0.34
(-1)3
25
-4
3
4
0.3
104
判断:(对的画“√”,错的画“×”.)
(1)
32
=
3×2
=
6;
(
)
(2)
(-2)3
=
(-3)2;
(
)
(3)
-32
=
(-3)2;
(
)
(4)
;
(
)
(5)
.
(
)
X
X
X
X
X
32
=
3×3=9
(-2)3
=-8;
(-3)2=9
-32
=-9;
(-3)2=9
-24=-2×2×2×2=-16
(-4)2底数是______指数是______(-4)2=_______
-4
2
16
34表示___个___
相乘
4
3
(-2)3=______
-8
(+1)2003
-(-
1)2002=___
0
-
14+1=______
0
3或-3
______的平方等于9
不计算下列各式的值,你能确定其符号吗?
你能得到什么规律吗?说出你的根据.
(1)(-2)51
;(2)(-2)50
;
(3)250
;
(4)251;
(5)02
020
;(6)12
021.
你能迅速判断下列各幂的正负吗?
手工拉面是我国的传统面食.制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣,如此反复操作,连续扣六七次后便成了许多细细的面条.假如拉扣了6次,你能算出共有多少根面条吗?
第一次
拉扣后
第二次
拉扣后
第三次
拉扣后
…
你认为国王的国库里有这么多米吗?
猜猜看
…
